Sinu

In matematica, in particulari in trigunumitria, datu un triangulu rittangulu, u sinu di unu di i dui anguli interni aghjacenti à l'iputenusa hè difinitu com'è u rapportu trà i lunghezzi di u catetu oppostu à l'angulu è di l'iputenusa.

Più in generali, u sinu d'un angulu $\alpha$ , espressu in gradi o radianti, hè una quantità chì dipendi solu da $\alpha$ , custruita usendu a circumfarenza unitaria.

Difiniscendu com'è $\sin(x)$ u sinu in l'angulu $x$ , s'otteni a funzioni sinu, una funzioni trigunumetrica di fundamintali impurtanza in l'analisa matematica.

Difinizioni

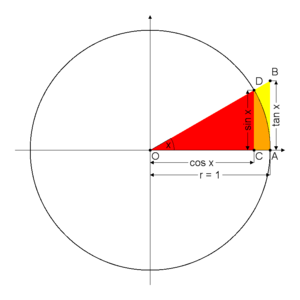
In u triangulu rossu annantu à a figura, u sinu di $x$ hè datu da

\sin(x)={\overline {DC}}

Più in generali, si difinisci u sinu d'un angulu $x$ (aspressu in gradi o radianti) à parta da a circumfarenza guniumetrica, vali à dì da a circumfarenza di raghju unitariu in u pianu cartisianu. Presa a mezaretta chì esci da l'urighjina chì forma un angulu $x$ incù l'assu di l'ascissi com'è annantu à a figura, u sinu di l'angulu hè dunqua difinitu com'è u valori di a cuurdinata $y$ di u puntu d'intarsizioni trà a mezaretta è a circumfarenza (nantu à a figura, hè a lunghezza di u sigmentu $CD$ ).

U duminiu di a funzioni sinu hè l'insemu di i numari riali, mentri u cuduminiu hè l'intarvallu riali $[-1;+1]$ , veni à dì applichendu tali funzioni à qualunqua numaru riali s'otteni sempri un numaru riali cumpresu trà $-1$ è $+1$ , estremi inclusi.

A tavuledda siguenti esponi i principali valori nutevuli assunti da a funzioni sinu:

$x$ in radianti	0	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {\pi }{2}}$	$\pi$	${\frac {3\pi }{2}}$	$2\pi$
$x$ in gradi	0°	30°	45°	60°	90°	180°	270°	360°
$\sin(x)$	$0$	${\frac {1}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {3}}{2}}$	$1$	$0$	$-1$	$0$

In i testi di matematica u sinu di $x$ hè di solitu indicatu incù a nutazioni $\sin(x)$ , induva $\sin$ hè un'abbriviazioni di u latinu sinus usata ancu in i paesi di lingua inglesa.

Esisti un'altra difinizioni di sinu chì si cullega à i rutazioni: u sinu d'un angulu $x$ hè u cumpunenti longu l'assu di l'urdinati di u virsori $i$ , virsori di l'assu di l'ascissi, ghjiratu di $x$ .

Funzioni sinu

A funzioni sinu hè difinita assucendu à $x$ u sinu di l'angulu $x$ (rapprisintatu in radianti), è hè indicata incù $\sin(x)$ . postu ch'è $x$ è $x+2\pi$ definiscini u stessu angulu, a funzioni sinu hè una funzioni piriodica di periodu $2\pi$ (induva $2\pi$ hè l'angulu ghjiru).

Sinu è cusinu

Trà sinu è cusinu esisti a rilazioni fundamintali:

\sin ^{2}x+\cos ^{2}x=1,

chì hè cunsiquenza di u tiurema di Pitagora. Infatti in u triangulu $OCD$ in a figura in altu u cusinu di $x$ hè difinitu com'è

\cos(x)={\frac {\overline {OC}}{\overline {OD}}}.

D'altra parti u tiurema di Pitagora applicatu à u triangulu $OCD$ furnisci a rilazioni: ${\overline {DC}}^{2}+{\overline {OC}}^{2}={\overline {OD}}^{2},$ è dunqua: $\sin ^{2}x+\cos ^{2}x=\left({\frac {\overline {DC}}{\overline {OD}}}\right)^{2}+\left({\frac {\overline {OC}}{\overline {OD}}}\right)^{2}={\frac {{\overline {DC}}^{2}+{\overline {OC}}^{2}}{{\overline {OD}}^{2}}}={\frac {{\overline {OD}}^{2}}{{\overline {OD}}^{2}}}=1.$ Vali ancu a rilazioni:

\sin(x)=\cos \left(x-{\frac {\pi }{2}}\right).

Com'è par u cusinu, a cusecanti d'un angulu hè $1$ divisu u sinu di l'angulu.

Prubità analitichi di a funzioni sinu

A funzioni sinu (in turchinu) è a so apprussimazioni data da u pulinomiu di Taylor di 7º gradu (rusulatu).

A dirivata di a funzioni sinu hè a funzioni cusinu. Avemu veni à dì: $\sin 'x=\cos x.$ A dirivata siconda hè inveci: $\sin ''x=-\sin x.$ A funzioni sinu hè una funzioni analitica, è a so espansioni in seria di Taylor hè: $\sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}.$ In analisa matematica st'ugualità hè spessu usata par difiniscia u sinu. A stessa seria difinisci u sinu com'è funzioni olumorfa annantu à tuttu u pianu cumplessu.

Equazioni fundamintali rilativi à u sinu

Si rapportani quì di seguitu parechji equazioni fundamintali riguardu à a funzioni sinu;

\sin ^{2}x+\cos ^{2}(x)=1,

\sin(x\pm y)=\sin x\cos y\pm \cos x\sin y,

\cos(x\pm y)=\cos x\cos y\mp \sin x\sin y,

incù l`aghjunta di a cundizioni ch'è:

0<x\cos x<\sin x<x{\text{ par }}0<x<1.

Esisti ancu un'idantità trigunumetrica chì metti in rilazioni a funzioni sinu è a funzioni tangenti:

\sin(x)={\frac {2\tau }{1+\tau ^{2}}}\quad {\text{ incù }}\quad \tau =\tan {\frac {x}{2}}.

st'idantità si svela di fundamintali impurtanza in a risuluzioni d'equazioni guniumetrichi in a quali a scunnisciuta figura com'è argumentu sii d'un sinu sii d'un cusinu (o di funzioni dirivati da quiddi). Esisti, infatti, un'idantità analoga par ciò chì riguarda u cusinu, u chì parmetti a risuluzioni di l'equazioni in a scunnisciuta $\tau$ .

Difinizioni currilati

U reciprocu di u sinu (difinitu induva u sinu hè diffarenti da zeru) hè a cusecanti

\csc x={\frac {1}{\sin x}}

A funzioni sinu, ristretta à l'intarvallu $\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$ hè iniettiva è dunqua hà una inversa, chjamata arcusinu (indicatu incù $\arcsin$ o incù $\sin ^{-1}$ chì ripiglia a nutazioni di a funzioni inversa). Par difinizioni s'hà dunqua:

x=\arcsin y\Longleftrightarrow y=\sin x,\quad -{\frac {\pi }{2}}\leq x\leq {\frac {\pi }{2}},\quad -1\leq y\leq 1.

Storia è urighjina di u nomu

U cuncettu di sinu fù introduttu da u matematicu è astrunomu indiana Aryabhata I (in devanāgarī: आर्यभट) (476 - 550) in a so opara Aryabhatiya (499).

U sinu hè par difinizioni a mità d'una corda, veni à dì un sigmentu chì unisci dui punti (ditti estremi) d'una circumfarenza. A parola sanscrita par mità corda hè jya-ardha, calchì volta sustituitu incù ardha-jya è abbriviatu in jya (corda). Stu terminu fù impurtatu in a lingua araba com'è jiba, un terminu senza significatu prima di tandu ma chì riflittia a prununcia funetica di u nomu jya. Sicondu i reguli di a lingua araba, 'ssu nomu fù scrittu incù i dui cunsunanti jb, senza vucali. Più dopu, quandu i traduttori uccidintali ebbini cunniscenza di i fonti arabi, intarpritàni a parola jb com'è jaib, chì u so significatu era baia. Infini, u talianu Gherardo da Cremona (1114 - 1187) tradussi a parola in latinu com'è sinus, di a quali u significatu era par appuntu baia.

U sinu d'un angulu hè indicatu incù $\mathrm {sin} (x)$ .

Da veda dinò

Noti

Fonti

'Ss'articulu pruveni in parti o in tutalità da l'articulu currispundenti di a wikipedia in talianu.