Galerkinova metoda

Galerkinova metoda(často téžRitzova-Galerkinova metoda,dle přepisu zruštinyGaljorkinova metoda) je postup používaný při řešení soustavyparciálních diferenciálních rovnic,jehož princip spočívá v nahrazení původní rovnice, tzv. silné formulace, její integrální formou, tzv. slabým řešením, a následnou diskretizací slabého řešení. Galerkinova metoda, která patří do třídy metod vážených reziduí, se stala základemmetody konečných prvků.Ve dvacátých letech 20. století ji významně rozpracovali ruští vědci, zejménaIvan BubnovaBoris Grigorjevič Galjorkin(také přepisovánGalerkin), kteří navázali na práci německého matematikaWalthera Ritze.Prudký vývoj pak od padesátých let zaznamenala Metoda konečných prvků zejména díky rozmachu výpočetní techniky. V současnosti je metoda konečných prvků nejpoužívanější metodou pro numerické simulace nejrůznějších fyzikálních problémů.

Slabé řešení diferenciální rovnice

Uvažujme diferenciální rovnici pro funkci$u\,\!$na oblasti$\Omega \,\!$splňující homogenníDirichletovské podmínkyna hranici oblasti$\partial \Omega \,\!$.

$L(u(x))=p(x),u|_{\partial \Omega }=0$

kde$L\,\!$je lineární diferenciální operátor. Definujemeskalární součin

$\langle f,g\rangle =\int _{\Omega }f(x)g(x)\mathrm {d} \Omega \,\!$

a pak funkce, pro něž je integrál$\int _{\Omega }f(x)^{2}\mathrm {d} \Omega \,\!$konečný, a které splňují nulové okrajové podmínky, tvoří nekonečně-dimenzionální vektorový prostor$V\,\!$.Existuje tedyvektorová báze$\{\phi _{i}\}_{i=1}^{\infty }\,\!$a libovolnou funkci z prostoru$V\,\!$lze vyjádřit jakolineární kombinacibázových funkcí$f=\sum _{i=1}^{\infty }\ Alpha _{i}\phi _{i}$, přičemž platí-li pro nějakou funkci$f\,\!$,že její skalární součin s libovolnou z bázových funkcí je nulový, pak funkce$f\,\!$jenulovým prvkemvektorového prostoru$V\,\!$.

$\langle f,\phi _{i}\rangle =0,\forall i\Rightarrow f\equiv 0$

To vede k definici slabého řešení$u\,\!$,které místo původní diferenciální rovnice splňuje rovnici

$\langle Lu(x)-p(x),\phi _{i}\rangle =0,\forall i$

Slabé řešení je tedy definováno integrální rovnicí

$\int _{\Omega }L(u)\phi _{i}\mathrm {d} \Omega =\int _{\Omega }p\phi _{i}\mathrm {d} \Omega,\forall i$

Existuje-li silné řešení, a je-li dostatečné hladké, pak je rovno slabému řešení.

Diskretizace slabého řešení

Princip Galerkinovy metody spočívá v nahrazení nekonečně-dimenzionálního prostoru$V\,\!$jeho konečně-dimenzionálním podprostorem$V_{n}\,\!$.Řešení$u_{n}\,\!$pak hledáme ve tvaru konečné řady$f=\sum _{i=1}^{n}\ Alpha _{i}\phi _{i}\,\!$,které splňuje slabou formulaci

$\int _{\Omega }L(u_{n})\phi _{i}\mathrm {d} \Omega =\int _{\Omega }p\phi _{i}\mathrm {d} \Omega,\forall i=1,\ldots,n$

čímž dostáváme soustavu$n\,\!$lineárních rovnic pro$n\,\!$neznámých koeficientů$\ Alpha _{i}\,\!$

$A_{ij}\ Alpha _{j}=F_{i}\,\!$

Matice

$A_{ij}=\int _{\Omega }\phi _{i}L(\phi _{j})\mathrm {d} \Omega \,\!$

se z historických důvodů nazývámaticí tuhostia vektor

$F_{i}=\int _{\Omega }p\phi _{i}\mathrm {d} \Omega \,\!$

vektorem zatížení.Pro bázové funkce se používá označenítestovací funkce.

Vztah slabého řešení a variačních úloh

Je-li$a(u,v)\,\!$symetrická bilineární forma, pak minimalizace funkcionálu

$J(u)=\inf _{v\in V}J(v),$

který je dán výrazem

$J(v)={\frac {1}{2}}a(v,v)-F(v),$

je ekvivalentní hledání řešení

$a(u,v)=F(v)\quad \forall v\in V,$

neboť

$J(v)={\frac {1}{2}}a(v,v)-a(u,v)={\frac {1}{2}}a(v-u,v-u)-{\frac {1}{2}}a(u,u)$

a tedy funkcionál nabývá minima pro$v=u\,\!$,protože člen$a(u,u)\,\!$je konstantní. Pokud diferenciální rovnice popisuje fyzikální systém mající potenciální energii, vyjadřuje funkcionál$J\,\!$energii systému.

Příklad

Řešme rovnici${\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}=x$s homogenními okrajovými podmínkami$y(0)=y(1)=0\,\!$.Rovnici přenásobíme testovací funkcí$\phi \,\!$splňující okrajové podmínky$\phi (0)=\phi (1)=0\,\!$a integrujeme na intervalu $<0,1>\,\!$,dostáváme

$\int _{0}^{1}{\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}\phi \mathrm {d} x=\int _{0}^{1}x\phi \mathrm {d} x$

Integrací per partespak dále upravíme levou stranu

$\left[{\frac {\mathrm {d} y}{\mathrm {d} x}}\phi \right]_{0}^{1}-\int _{0}^{1}{\frac {\mathrm {d} y}{\mathrm {d} x}}{\frac {\mathrm {d} \phi }{\mathrm {d} x}}\mathrm {d} x=\int _{0}^{1}x\phi \mathrm {d} x$

a díky tomu, že bázové funkce$\phi \,\!$splňují okrajové podmínky, dostáváme slabou formulaci problému

$-\int _{0}^{1}{\frac {\mathrm {d} y}{\mathrm {d} x}}{\frac {\mathrm {d} \phi }{\mathrm {d} x}}\mathrm {d} x=\int _{0}^{1}x\phi \mathrm {d} x$

která musí být splněna pro všechny testovací funkce.

Příklad: přesné řešení diferenciální rovnice a Galerkinovo řešení ve tvaru konečné řady pro různé délky řady.

Zvolme bázové funkce ve tvaru$\phi _{i}=\sin(i\pi x)\,\!$a řešení hledejme jako konečnou řady$y=\sum _{i=1}^{n}\ Alpha _{i}\phi _{i}=\sum _{i=1}^{n}\ Alpha _{i}\sin(i\pi x)$.Díky volbě bázových funkcí je matice tuhosti diagonální, neboť$A_{ij}=-\int _{0}^{1}ij\pi ^{2}\cos(i\pi x)\cos(j\pi x)\mathrm {d} x=-{\frac {ij\pi ^{2}}{2}}\delta _{ij}$,kde$\delta _{ij}$jeKroneckerovo delta.Vektor zatížení je$F_{i}=\int _{0}^{1}x\sin(i\pi x)\mathrm {d} x={\frac {(-1)^{(i+1)}}{i\pi }}$.Pro koeficienty$\ Alpha _{i}\,\!$tedy platí$-{\frac {ij\pi ^{2}}{2}}\delta _{ij}\ Alpha _{j}={\frac {(-1)^{(i+1)}}{i\pi }}$a hledané řešení má tedy tvar

$y=\sum _{i=1}^{n}(-1)^{i}{\frac {2}{i^{3}\pi ^{3}}}\sin(i\pi x).$

Metoda konečných prvků

Metoda konečných prvkůje zvláštním případem Galerkinovy metody, při které jsou jako testovací funkce použity funkce s kompaktním nosičem. Díky tomu je matice tuhostiřídká,v ideálním případě pásová, a při numerickém řešení soustavy rovnic lze s výhodou použít efektivní algoritmy.

Testovací po částech lineární funkce (modře) na intervalu$<0,1>\,\!$a příklad jejich lineární kombinace (červeně).

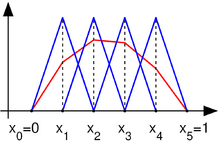
Výše uvedený příklad lze řešit metodou konečných prvků: interval$<0,1>\,\!$rozdělme na$n\,\!$intervalů a definujme bázové funkce

$f_{i}(x)=\left\{{\begin{matrix}{\frac {x-x_{i-1}}{x_{i}-x_{i-1}}},&x\in <x_{i-1},x_{i}>\\1-{\frac {x-x_{i}}{x_{i+1}-x_{i}}}&x\in <x_{i},x_{i+1}>\\0&\mathrm {jinak} \end{matrix}}\right.$

Příklad: přesné řešení diferenciální rovnice a Galerkinovo řešení pro různé diskretizace oblasti.

Pro jednoduchost uvažujme, že délka všech intervalů$h=x_{i}-x_{i-1}\,\!$je stejná, potom matice tuhosti je diagonální

$A_{ij}={\begin{pmatrix}-{\frac {2}{h}}&{\frac {1}{h}}&0&0&0&0\\{\frac {1}{h}}&-{\frac {2}{h}}&{\frac {1}{h}}&0&0&0\\0&{\frac {1}{h}}&-{\frac {2}{h}}&{\frac {1}{h}}&0&0\\0&0&{\frac {1}{h}}&-{\frac {2}{h}}&{\frac {1}{h}}&0\\0&0&0&{\frac {1}{h}}&-{\frac {2}{h}}&{\frac {1}{h}}\\0&0&0&0&{\frac {1}{h}}&-{\frac {2}{h}}\\\end{pmatrix}}$

Řešení opět hledáme ve tvaru konečné řady$y_{h}(x)=\sum _{i=1}^{n}\ Alpha _{i}f_{i}(x)\,\!$.Jednotlivé složky vektoru zatížení$F_{i}=\int _{0}^{1}xf_{i}(x)\mathrm {d} x\,\!$lze sice v tomto jednoduchém případě řešit analyticky, ale v obecném případě je nutné použítnumerickou integraci,což může platit i pro prvky matice tuhosti. V praxi se jak pro výpočet jednotlivých prvků vektorů zatížení, tak i jednotlivých prvků matice tuhosti, používajíGaussovy kvadraturní vzorce.

Courantova bázová funkce na triangulované oblasti

Jedním z hlavních problémů metody konečných prvků je síťování (triangulace) oblasti, které v inženýrské praxi představuje často časově nejvíce náročnou část analýzy.Dvoudimenzionální sítě jsou obvykle tvořeny trojúhelníky nebo čtyřúhelníky, zatímco třídimenzionální sítě jsou obvykle tvořeny čtyřstěny nebo šestistěny. Výsledky automatického síťování třídimenzionálních oblastí často vyžadují manuální opravy výsledné sítě a proto se automatickému generovaní sítí věnuje od 70. let minulého století velké úsilí.Přesto zůstává automatické generace sítě stále nevyřešeným problémem. Je-li hranice vyšetřované oblasti křivočará, je aproximace oblastimnohostěnem (polyedrem)zdrojem dalších nepřesností metody, proto se někdy uvažují křivočaré prvky, což je však v praxi velmi obtížné.

Dalším zdrojem chyb je numerická integrace použitá při výpočtu jednotlivých prvků vektoru zatížení a matice tuhosti i numerické chyby při vlastním řešení soustavy lineární rovnic s řídkou maticí, při níž se s ohledem na velikost matice často používají iterační metody (Jacobiho metoda, Gauss-Seidelova metoda aj.).

Odhad chyby metody

Pro odhad chyby diskretizovaného řešení$y_{h}\,\!$má klíčový významCéaovo lemmapodle něhož pro funkce zeSobolevova prostoru$H^{1}\,\!$existuje taková konstanta$C\,\!$,že

$\|y-y_{h}\|_{H^{1}}\leq C\inf _{v_{h}\in V_{h}}\|y-v_{h}\|_{H^{1}},$

Norma$\|v\|_{H^{1}}={\sqrt {<v,v>}}$je přitom definována pomocí skalárního součinu na prostoru$H^{1}\,\!$

$<f,g>=\int _{\Omega }^{}f(x)g(x)\mathrm {d} \Omega +\sum _{k=1}^{N}{\frac {\partial f}{\partial x_{k}}}{\frac {\partial g}{\partial x_{k}}}\mathrm {d} \Omega$

Céanovo lemma říká, že i kdybychom znali přesné řešení$y\,\!$zkoumané diferenciální rovnice, na prostoru$V_{h}\,\!$bychom nenalezli lepší aproximaci řešení, než je právě$y_{h}\,\!$.

Ve výše uvedeném případě uvažujme po částech lineární funkci${\tilde {y}}$,která aproximuje přesné řešení$y\,\!$ve všech uzlových bodech, tj. platí$y(x_{i})={\tilde {y}}(x_{i}),\,\forall i=0,1,\ldots N$.Pro každý interval$<x_{i},x_{i+1}>\,\!$lze pomocíTaylorova rozvojepsát

${\tilde {y}}(x)={\tilde {y}}(x_{i})+{\tilde {y}}'(x_{i})(x-x_{i})$

$y(x)=y(x_{i})+y'(x_{i})(x-x_{i})+{\frac {1}{2}}y''(\xi _{x})(x-x_{i})^{2}$,

kde$\xi _{x}\,\!$je nějaký bod v intervalu$<x_{i},x>\,\!$.Dosadíme-li za$x\,\!$koncový bod intervalu$x_{i+1}\,\!$a odečteme-li od sebe rozvoje přesného řešení$y\,\!$a jeho interpolaci${\tilde {y}}$,dostaneme

${\tilde {y}}'(x_{i})-y'(x_{i})={\frac {1}{2}}y''(\xi _{h})(x_{i+1}-x_{i}),$

kde$\xi _{h}\,\!$je nějaký bod v intervalu$<x_{i},x_{i+1}>\,\!$. Odečteme-li pak od sebe rozvoje přesného řešení$y\,\!$a jeho interpolaci${\tilde {y}}$ve vnitřním bodu intervalu$x\,\!$,dostaneme

$|{\tilde {y}}(x)-y(x)|\leq {\frac {1}{2}}|y''(\xi _{h})|(x_{i+1}-x_{i})(x-x_{i})+{\frac {1}{2}}|y''(\xi _{x})|(x_{i+1}-x)^{2}\leq (x_{i+1}-x_{i})^{2}\max _{\xi \in <x_{i},x_{i+1}>}|y''(\xi )|.$

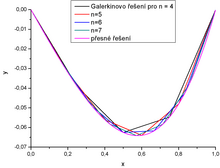
Pro odhad chyby v normě$H^{1}\,\!$pak platí $\|y-y_{h}\|_{H^{1}}\leq Ch\|y''\|,$kde$h\,\!$je největší z intervalů$<x_{i},x_{i+1}>\,\!$.Tento výsledek má fundamentální význam pro konvergenci, neboť říká, že s jemnější diskretizací ($h\to 0$) se rozdíl přesného a diskretizovaného řešení zmenšuje. Céaovo lemma má proa priorníodhad chyby velký význam rovněž z toho důvodu, že umožňuje místo aproximačních vlastností bázových funkcí vyšetřovat aproximační vlastnosti vektorových prostorů$V_{h}\,\!$.Obecný odhad chyby založený na Céaově lemmatu lze pro některé speciální třídy úloh upřesnit

Aplikace na fyzikální problémy

Galerkinova metoda, nejčastěji ve formě metody konečných prvků, se používá k numerickému řešení rovnicevedení tepla,rovnic popisujícíchgravitační,magnetickýčielektrický potenciál,vlnové rovnicinebo rovnic mechaniky kontinua (např.Navierova–Stokesova rovnice). Historicky prvními úlohami, pro jejichž řešení byla použita Galerkinova metoda, byly výpočty pružnosti a pevnosti (např.vlastní kmity).

Průhyb nosníku

Klasickou úlohou je průhyb nehomogenníhonosníkuproměnného průřezu. Je-li nosník délky$L\,\!$namáhaný příčným zatížením$q(x)\,\!$na obou stranách vetknutý, platí pro průhyb$u(x)\,\!$rovnice

$(E(x)I(x)u''(x))''=q(x),\qquad u(0)=u(L)=u'(0)=u'(L)=0$,

kde$E(x)\,\!$jeYoungův modul pružnostia$I(x)\,\,$je kvadratický moment průřezu. Pro odvození slabého řešení definujme vektorový prostor funkcí splňujících zadané homogenní okrajové podmínky

$V=\{v\in L^{2}(\Omega ):\,v(0)=v(L)=v'(0)=v'(L)\}$

a slabé řešení je pak definováno rovnicí

$a(u,v)=F(v)\qquad \forall v\in V$,

kde bilineární forma je dána předpisem

$a(u,v)=\int _{0}^{L}E(x)I(x)u''(x)v''(x)\mathrm {d} x$

a vektor zatížení je

$F(v)=\int _{0}^{L}q(x)v(x)\mathrm {d} x.$

Ke stejné slabé formulaci bychom dospěli minimalizací funkcionálu

$J(v)={\frac {1}{2}}\int _{0}^{L}E(x)I(x)(v(x)'')^{2}\mathrm {d} x-\int _{0}^{L}q(x)v(x)\mathrm {d} x,$

kde fyzikální význam prvního členu je potenciální energie vnitřních sil (energie napjatosti) a druhý člen představuje potenciální energii vnějších sil. Vzhledem k tomu, že vyšetřovaná rovnice je čtvrtého řádu, je na testovací funkce kladena podmínka spojitosti prvních derivací v celém intervalu. Při rozdělení oblasti na$N\,\!$intervalů lze jako testovací funkce použítkubické splinové funkceurčené předpisem

${\begin{array}{ll}v^{2i-1}(x_{j})=\delta _{ij},&(v^{2i-1})'(x_{j})=0\\v^{2i}(x_{j})=0,&(v^{2i})'(x_{j})=\delta _{ij}\\\end{array}}\quad \forall i,j=1,\ldots,N-1$

Označíme-li délku intervalu$<x_{i-1},x_{i}>\,\!$jako$h_{i}\,\!$,pak testovací funkce jsou dány vztahy

${\begin{array}{ll}v^{2i-1}(x)=-2(x-x_{i-1})^{2}(x-x_{i}-h_{i}/2)/h_{i}^{3},&x\in <x_{i-1},x_{i}>\\v^{2i-1}(x)=2(x-x_{i+1})^{2}(x-x_{i}-h_{i+1}/2)/h_{i+1}^{3},&x\in <x_{i},x_{i+1}>\\v^{2i}(x)=2(x-x_{i-1})^{2}(x-x_{i})/h_{i}^{2},&x\in <x_{i-1},x_{i}>\\v^{2i}(x)=2(x-x_{i+1})^{2}(x-x_{i})/h_{i+1}^{2},&x\in <x_{i},x_{i+1}>\\v^{2i-1}(x)=v^{2i}(x)=0,&x\notin <x_{i-1},x_{i+1}>\\\end{array}}$

Zajímavou vlastností diskretizovaného řešení je, že je-li nosník homogenní a průřez nosníku konstantní, pak diskretizované řešení nemá v uzlových bodech$x_{i}\,\!$žádnou diskretizační chybu.

Stacionární vedení tepla

Stacionárnívedení teplav D-dimenzionální oblasti je popsáno rovnicí

$-\sum _{i,j=1}^{D}{\frac {\partial }{\partial x_{i}}}\left(k_{ij}(x){\frac {\partial T(x)}{\partial x_{j}}}\right)=f(x).$

Je-li prostředí homogenní a isotropní (tj.$k_{ij}\,\!$je jednotková matice), přechází rovnice na tzv.Poissonovou rovnici

$-\Delta T(x)=q(x),$

která je významná i v teorii potenciálu. Nejčastějšími okrajovými podmínkami jsou Dirichletova homogenní podmínka$T=0\,\!$,jejíž fyzikálním významem je zadaná teplota na hranici oblasti, nebo homogenní Neumannova podmínka na normálovou derivaci${\frac {\partial T}{\partial \mathbf {n} }}=0$,resp.$\sum _{ij}a_{ij}{\frac {\partial T}{\partial x_{j}}}n_{i}=0$pro neisotropní prostředí, jejíž fyzikálním významem je nulový tepelný tok přes hranici oblasti (tj. tepelně izolovaná hranice). Přenásobením rovnice vedení tepla libovolnou testovací funkcí a použitímGreenovy formule(zobecněná integraceper partesve více dimenzích)

$\int _{\Omega }{\frac {\partial v}{\partial x_{j}}}w\mathrm {d} \Omega +\int _{\Omega }v{\frac {\partial w}{\partial x_{j}}}\mathrm {d} \Omega =\int _{\partial \Omega }vwn_{j}\mathrm {d} S$

dostaneme variační formulaci

$\int _{\Omega }\sum _{ij}a_{ij}{\frac {\partial T}{\partial x_{j}}}{\frac {\partial v}{\partial x_{i}}}\mathrm {d} \Omega -\int _{\partial \Omega }\sum _{i,j}a_{ij}{\frac {\partial T}{\partial x_{j}}}n_{i}v\mathrm {d} S=\int _{\Omega }qv\mathrm {d} \Omega.$

Okrajové podmínky vyřešíme volbou vektorového prostoru testovacích funkcí: pro homogenní Dirichletovu podmínku zvolme

$V=\left\{v\in L^{2}(\Omega ),{\frac {\partial v}{\partial x_{j}}}\in L^{2}(\Omega ),v=0|\partial \Omega \right\},$

kde$L^{2}(\Omega )\,\!$značí vektorový prostor funkcí, pro něž je integrál$\int _{\Omega }f(x)^{2}\mathrm {d} \Omega \,\!$konečný, a integrál přes hranici oblasti ve slabé formulaci vymizí díky$v=0|\partial \Omega \,\!$.V případě homogenní Neumannovy podmínky stačí volit vektorový prostor testovacích funkcí

$V=\left\{v\in L^{2}(\Omega ),{\frac {\partial v}{\partial x_{j}}}\in L^{2}(\Omega )\right\}$

a integrál přes hranici oblasti vymizí díky podmínce na nulový tepelný tok přes hranici. Díky tomu je podmínka na (normálovou) derivaci označována za přirozenou.

Slabé řešení stacionární rovnice vedení tepla je tedy

$\int _{\Omega }\sum _{ij}a_{ij}{\frac {\partial T}{\partial x_{j}}}{\frac {\partial v}{\partial x_{i}}}\mathrm {d} \Omega =\int _{\Omega }qv\mathrm {d} \Omega \quad \forall v\in V,$

přičemž vektorový prostor$V\,\!$je určen předepsanými okrajovými podmínkami.

Bezsíťová Galerkinova metoda

Obtíže při konstrukci výpočetních sítí vedly k rozvoji celé třídy tzv. bezsíťových metod. Tyto metody lze s výhodou uplatnit pro řešení problémů, kdy se zkoumaná oblast deformuje, např. úlohy s pohyblivou hranicí, šíření trhlin nebo simulace tavení. Typickým zástupcem bezsíťových metod je bezsíťová Galerkinova metoda,při níž je konečně-prvková síť nahrazena uzlovými body, se kterými jsou asociovány váhové funkce s omezeným nosičem. Diskretizované řešení se hledá ve tvaru

$\phi ^{h}=\sum _{i=1}^{m}p_{i}(x)a_{i}(x),$

kde$p_{i}(x)\,\!$jsou bázové funkce a$a_{i}(x)\,\!$jsou neznámé koeficienty závislé na poloze. V jednodimenzionálním případě s lineární bází je$m=2\,\!$a bázové funkce jsou$p_{1}=1\,\!$a$p_{2}=x\,\!$.Koeficienty$a(x)\,\!$se získají minimalizací funkce

$J=\sum _{i=0}^{N}w(x-x_{i})(\phi _{i}^{h}(x)-\phi _{i}^{h}(x_{i}))^{2},$

kde$w\,\!$jsou váhové funkce asociované s uzlovými body$x_{i}\,\!$,jejichž počet je$N\,\!$.

Historie

Základy metody položil německý matematikWalter Ritzv práci zabývající se výpočtem vlastních kmitů pružné desky.Pro výpočet polohy uzlových bodů, tzv.Chladniho obrazců,použil variační metodu. Ritzův přístup záhy získal velký ohlas u ruských vědců, kteří metodu zobecnili. Ruský inženýr a konstruktér ponorekIvan Grigorjevič Bubnovrozpoznal, že slabé řešení lze definovat i pro problémy, které nemají funkcionál energie.Metodu dále zobecnilBoris Grigorjevič Galjorkin,když ukázal, že podmínka ortogonality bázových funkcí není nutná.

Původní Ritzovu myšlenku obohatilRichard Courant,když navrhl hledat přibližné řešení variačního problému ve tvaru spojité lineární funkce na triangulované oblasti.S rozvojem výpočetní techniky pak nastal bouřlivý rozvoj metody konečných prvků, přičemž poprvé byl termínmetoda konečných prvkůpoužit v roce 1960.

Přestože k numerickému řešení diferenciálních rovnic se metoda konečných prvků (MKP) používala zejména v leteckém průmyslu již od padesátých let,teoretické studium MKP začalo až v polovině šedesátých let, kdy brněnský matematikMiloš Zlámaljako první dokázal konvergenci MKPa stal se tak světově uznávaným odborníkem.

Odkazy

Literatura

Česky

• I. Babuška, M. Práger, E. Vitásek: Numerické řešení diferenciálních rovnic, SNTL Praha, 1964.
• Z. Bittnar, P. Řeřicha. Metoda konečných prvků v dynamice konstrukcí, SNTL Praha, 1981.
• J. Haslinger. Metoda konečných prvků pro řešení eliptických rovnic a nerovnic. Skripta MFF UK, SPN Praha, 1980.
• V. Kolář, J. Kratochvíl, F. Leitner, A. Ženíšek. Výpočet plošných a prostorových konstrukcí metodou konečných prvků. SNTL, Praha 1979.
• V. Kolář, I. Němec, V. Kanický. FEM – principy a praxe metody konečných prvků. Computer Press, Praha, 1997.
• K. Rektorys.Variační metody v inženýrských problémech a v problémech matematické fyziky, Academia, Praha, 1999.
• E. Vitásek. Numerické metody, SNTL, Praha, 1987.

Anglicky

• I. Babuška, T. Strouboulis: The finite element method and its reliability, Oxford University Press, New York, 2001.
• S. C. Brenner, L. Ridgway Scott. The mathematical theory of finite element methods, New York, Springer 1994.ISBN0-8493-1668-5
• K. K. Gupta, J. L. Meek. A Brief History of the Beginning of the Finite Element Method, Int. J. for Num. Methods in Engineering, 39, 3761-3774, 1996.dostupné online^{[nedostupný zdroj]}
• K. H. Huebner, D. L. Dewhirst, D. E. Smith, T. G. Byrom. The Finite Element Method For Engineers, John Wiley, 2001.ISBN0-471-37078-9
• P. Šolín. Partial Differential Equations and the Finite Element Method, J. Wiley and Sons, 2005.ISBN0-4717-2070-4
• R L. Taylor. Ritz and Galerkin: the road to the Finite Element Method. Bulletin for the international association for computational Mechanics, 12:2–5, 2002.dostupné onlineArchivováno4. 7. 2011 naWayback Machine.
• L. T. Tenek, J. H. Argyris. Finite element analysis for composite structures. Springer 1998.ISBN978-0-7923-4899-3
• O. C. Zienkiewicz. The Finite Element Method in Engineering Science. McGraw Hill, London, 1971.

Autoritní data	NKC:ph548979 GND:4155831-5 LCCN:sh85052782 NLI:987007555547405171

Portály:Matematika