Spojité zobrazení

Spojité zobrazeníje pojem ztopologieamatematické analýzy. Je to takovézobrazení,které zobrazuje dostatečně blízkébodyblízko sebe. Tato vlastnost zobrazení se nazýváspojitost.Spojité zobrazení je zobecněním pojmuspojitá funkcenamnožinách čísel.

Neformální úvod

Spojitostje přirozená a očekávatelná vlastnost zobrazení. Pro reálnéfunkce spojitost znamená,žegraf funkceneobsahuje ostré skoky a vypadá jakosouvislá křivka.Pojem lze definovat nametrických prostorech,tedy na množinách, na kterých je možné měřit "vzdálenosti". Jedná se tedy například o množinybodůvrovině,anebo také nějakou množinu funkcí. V metrických prostorech spojitost znamená, že pokud se nějaký bod blíží jinému bodu, blíží se k sobě i obrazy.

Metrickoudefinicilze zobecnit natopologické prostory,tj. na ještě širší skupinu množin, než jsou metrické prostory. V topologii je spojitost definována tak, že množiny zachovávají některé své topologické vlastnosti. Spojité zobrazení například převádísouvislé množinyna souvislé,kompaktnína kompaktní a vzorotevřené množinyje otevřená množina. Tyto různé definice spojitosti jsou vzájemně kompatibilní.

Formální definice

V topologických prostorech

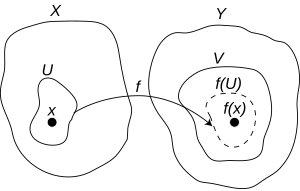
Zobrazení $f$ mezi topologickými prostory $X$ a $Y$ nazvemespojité,pokudvzorkaždé otevřené množiny v $Y$ jeotevřená množinav $X$ .

Ekvivalentní definice říká, že zobrazení $f$ jespojité v bodě $x\in X$ ,jestliže pro každéokolí $V$ bodu $f(x)$ existuje okolí $U$ bodu $x$ takové, že $f(U)\subseteq V$ .Zobrazení $f$ jespojité,pokud je $f$ spojité v každém $x\in X$ .

V metrických prostorech

Zobrazení $f$ zmetrického prostoruprostoru $(X,\rho )\,\!$ do $(Y,\sigma )\,\!$ je spojité, právě když pro každé $x_{0}\in X\,\!$ a kladné reálné číslo $\epsilon \,\!$ existuje kladné reálné $\delta \,\!$ takové, že pro každý bod $x\in X\,\!$ splňující $\rho (x,x_{0})<\delta \,\!$ platí $\sigma (f(x_{0}),f(x))<\epsilon \,\!$ .Jinými slovy, vzdálenost obrazů dvou bodů může být libovolně blízká, pokud zvolíme vzdálenost vzorů dostatečně blízko.

Ekvivalentně, zobrazení $f:\,X\to Y$ je spojité v bodě $x\in X\,\!$ ,jestliže platíimplikace

x_{n}\to x\Rightarrow f(x_{n})\to f(x)\,

.

Spojitá zobrazení na množinách čísel

Zobrazením mezi množinami čísel se častěji říkáfunkce.Funkcefje spojitá v boděx,pokud pro každé $\epsilon >0$ existuje $\delta >0\,\!$ takové, že $|x-y|<\delta \,\!$ implikuje $|f(x)-f(y)|<\epsilon \,\!$ .

Množinareálnýchakomplexníchčísel je však takétopologický prostor,generován otevřenýmiintervaly.Podobněmetrický prostoranormovaný lineární prostorjsou topologické prostory a různé definice spojitosti zobrazení mezi těmito prostory jsou ekvivalentní.

Vlastnosti spojitých zobrazení

Složeníspojitých zobrazení je opět spojité zobrazení.
Spojité zobrazení zachovávákompaktní množiny.Proto i složení $f\circ g:X\rightarrow Z$ spojitého zobrazení $f:Y\rightarrow Z$ s kompaktním zobrazením $g:X\rightarrow Y$ jezobrazení kompaktní.

Příklady spojitých a nespojitých zobrazení

Sčítání,odčítání,násobeníaděleníčísel jsou spojitá zobrazení (z "dvojic" čísel do čísel).
Mapazobrazující část krajiny se dá chápat jako spojité zobrazení. Tento koncept je formalizován v definicivariety.Varieta je zadána pomocíatlasu,který pozůstává ze spojitých map.
Projekcetopologickéhovektorového prostoruna nějaký podprostor je spojité zobrazení.
Lineární transformacekonečně rozměrného vektorového prostoru je spojitá.
Polynomiální funkceje spojité zobrazení. Podobně zobrazení z $\mathbb {R} ^{n}$ do $\mathbb {R} ^{m}$ ,kterého každá složka je polynomiální funkce.
Křivkaje spojité zobrazení z úsečky do nějakého topologického prostoru.
Skalární součinje spojité zobrazení z dvojic vektorů do čísel.
Funkce $f:\mathbb {R} \to \{0,1\}$ ,kteráracionálním číslůmpřiřadí nulu airacionálnímjednotku, je nespojitá.
Evoluční operátorvkvantové fyzice(popisuje vývoj fyzikálního systému v čase) je spojité zobrazení.
Násobení vLieově grupěje spojité.
Každé zobrazení zdiskrétního prostorudo libovolného metrického prostoru je spojité^{[pozn 1]}.
Mějme X prostor spojitých reálných funkcí na intervalu $\scriptstyle \left\langle 0,\,1\right\rangle$ spolu se supremovou normou (||f||:=sup |f(x)|) a nechťK(x,t)je spojitá funkce. Definujme $\scriptstyle A:\,X\to X,\ (Ax)(t)=\int _{0}^{1}K(t,\,s)x(s)ds$ .Pak $\scriptstyle A\,$ je spojité zobrazení v $\scriptstyle \ C\left(\left\langle 0,\,1\right\rangle \right)$ .
Příkladem spojitého zobrazení na topologickém prostoru, který není metrizovatelný, jefunkce $\aleph$ ,která ordinálnímu číslu $\ Alpha$ přiřadí $\ Alpha$ -tou nejmenší nekonečnoumohutnost.Jedná se o zobrazení navlastní třídě,ovšem pro každéordinální číslo $\beta$ (které je zároveň množinou ordinálních čísel) jerestrikcetéto funkce na $\beta$ spojitým^{[pozn 2]}zobrazením z $\beta$ doobrazu $\aleph [\beta ]$ .
Lineární zobrazení nekonečně rozměrného vektorového prostoru může, ale také nemusí být spojité. Nechť $X=C^{\infty }(\langle 0,1\rangle )$ je prostor hladkých funkcí spolu s maximovou normou||f||=sup |f(x)|.Pak derivace $D:X\to X$ je lineární nespojité zobrazení.^{[pozn 3]}.

Odkazy

Poznámky

↑Stačí si uvědomit, že pro diskrétní prostor platí $\scriptstyle \forall x,\,y\in X,x\neq y:\rho (x,y)=1.$
↑Pokud konverguje $\{\ Alpha _{n}\}\subseteq \beta \,\!$ k nějakému $\ Alpha \in \beta \,\!$ ,pak posloupnost $\{\aleph _{\ Alpha _{n}}\}$ konverguje k $\aleph _{\ Alpha }\ \,\!$ .Příkladem je posloupnost $\aleph _{0},\aleph _{1},\aleph _{2},\ldots,\!$ konvergující k $\aleph _{\ Omega },\!$ ,zvolíme-li $\beta =\ Omega +1$ a $\ Alpha _{n}=n\,\!$ pro každé přirozené číslon.
↑Vezměme $\scriptstyle f_{n}(t)=t^{n}/n,n\in \mathbb {N}$ ,pak $\scriptstyle ||f_{n}||=1/n\to 0$ ,ale velikosti obrazů jsou $||(f_{n})'||=||t^{n-1}||=1$

Související články

Externí odkazy

Obrázky, zvuky či videa k tématuspojitá funkcenaWikimedia Commons
TémaSpojitostve Wikicitátech

[1] Stačí si uvědomit, že pro diskrétní prostor platí $\scriptstyle \forall x,\,y\in X,x\neq y:\rho (x,y)=1.$

[2] Pokud konverguje $\{\ Alpha _{n}\}\subseteq \beta \,\!$ k nějakému $\ Alpha \in \beta \,\!$ ,pak posloupnost $\{\aleph _{\ Alpha _{n}}\}$ konverguje k $\aleph _{\ Alpha }\ \,\!$ .Příkladem je posloupnost $\aleph _{0},\aleph _{1},\aleph _{2},\ldots,\!$ konvergující k $\aleph _{\ Omega },\!$ ,zvolíme-li $\beta =\ Omega +1$ a $\ Alpha _{n}=n\,\!$ pro každé přirozené číslon.

[3] Vezměme $\scriptstyle f_{n}(t)=t^{n}/n,n\in \mathbb {N}$ ,pak $\scriptstyle ||f_{n}||=1/n\to 0$ ,ale velikosti obrazů jsou $||(f_{n})'||=||t^{n-1}||=1$

[pozn 1]

[pozn 2]

[pozn 3]