Logarithmus

AlsLogarithmus(Plural:Logarithmen;vonaltgriechischλόγοςlógos,„Verständnis, Lehre, Verhältnis “, undἀριθμός,arithmós,„Zahl “) einer Zahl bezeichnet man denExponenten,mit dem eine vorher festgelegte Zahl, dieBasis,potenziert werden muss, um die gegebene Zahl, denNumerus,zu erhalten. Logarithmen sind zunächst nur für positive reelle Zahlen definiert, auch die Basis muss positiv – und von 1 verschieden – sein.

Logarithmische Skaleneinteilung einesRechenschiebers(Detail)

Graph der Logarithmusfunktion zur Basis 2 (grün),e(rot) und 1/2 (blau)

Inhalblogarithmischer Auftragung(in Bezug auf diex-Achse) wird der Graph der Logarithmusfunktion zu einer Geraden. Hier beispielhaft dargestellt für denLogarithmus zur Basis 10.

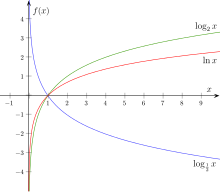
Der Logarithmus einer positiven reellen Zahl$x$zur Basis$b$ist also der Wert des Exponenten, wenn$x$alsPotenzzur Basis$b$dargestellt wird, also diejenige Zahl$y$,welche die Gleichung$b^{y}=x$löst. Man schreibt$y=\log _{b}(x)$;weitere Notationen sieheBezeichnungen.DasLogarithmieren,d. h. der Übergang von$x$zu$\log _{b}(x)$,ist damit eineUmkehroperationdesPotenzierens.Die Funktion, die bei gegebener fester Basis$b$jeder positiven Zahl ihren Logarithmus zuordnet, nennt manLogarithmusfunktionzur Basis$b$.

Mit Logarithmen lassen sich sehr stark wachsende Zahlenreihen übersichtlich darstellen, da der Logarithmus für große Zahlen viel langsamer steigt als die Zahlen selbst. Wie die Gleichung$\log _{b}(x\cdot y)=\log _{b}(x)+\log _{b}(y)$zeigt, kann man durch Logarithmieren eine Multiplikation durch die viel weniger rechenintensive Addition ersetzen. Auch beschreiben Logarithmen auf mathematisch elegante Weise viele technische Prozesse sowie Phänomene der Natur wie etwa das Verhalten einer Halbleiter-Diode,die Spirale einesSchneckenhausesoder dieWahrnehmung unterschiedlicher Lautstärkendurch das menschlicheOhr.

Entsprechende mathematische Berechnungen sind bereits aus der Zeit vor Christi Geburt ausIndienüberliefert. Der BegriffLogarithmuswurde vonJohn Napierim frühen 17. Jahrhundert geprägt. Napier zu Ehren wird derNatürliche Logarithmus(s. u.) manchmal auchNapierscher LogarithmusoderNeperscher Logarithmusgenannt.

Überblick

Die Verwendung des Logarithmus lässt sich bis in dieindische Antikezurückverfolgen. Mit dem aufstrebenden Bankwesen und dem Fortschritt derAstronomieim Europa des 17. Jahrhunderts erlangte der Logarithmus immer mehr Bedeutung. Seine Funktionswerte wurden in Tabellenwerken, denLogarithmentafeln,erfasst, um sie nachschlagen zu können und nicht immer neu berechnen zu müssen. Diese Tabellen wurden schließlich durchRechenschieberund später durchTaschenrechnerverdrängt. Der Wechsel von den Tabellen zum Rechenschieber erfolgte in deutschen Schulen in den 1960er Jahren, der Wechsel zu Taschenrechnern ab den 1970er Jahren.

Zentrale Aspekte des Lebens lassen sich mit Hilfe von Logarithmen beschreiben. So nimmt zum Beispiel die Stärke eines Sinneseindrucks in Abhängigkeit von einer physikalischen Größe wie Helligkeit oder Lautstärke entsprechend dem Verlauf einer Logarithmusfunktion zu. Gleiches gilt für die wahrgenommeneTonhöhein Abhängigkeit von derFrequenzeines Tones.

Logarithmen erlangten ihre historische Bedeutung durch den Zusammenhang

$\log(xy)=\log x+\log y,$

der es erlaubt, eine Multiplikation durch eineAdditionauszudrücken.

Formal sind Logarithmen alleLösungen$x$der Gleichung

$a=b^{x}$

zu vorgegebenen Größen$a$und$b$.

Je nachdem, über welchem Zahlenbereich und für welche Größen dieseGleichungbetrachtet wird, hat sie keine, mehrere oder genau eine Lösung. Ist die Lösung eindeutig, dann wird sie alsder Logarithmus von$a$zur Basis$b$bezeichnet und man schreibt

$x=\log _{b}a$

Beispielsweise ist der Logarithmus von 8 zur Basis 2 gleich 3, geschrieben$\log _{2}8=3$,denn es ist$2^{3}=8$.

Falls die obige Gleichung nach$b$aufzulösen ist anstatt nach$x$,so ist die Lösung gegeben durch die$x$-teWurzelaus$a$.

Am bekanntesten und am weitesten verbreitet ist der Logarithmus über den positivenreellen Zahlen,der im Folgenden vornehmlich dargestellt wird.

Geschichte

Titelblatt zu Jost Bürgis Logarithmentafel von 1620

Indische Mathematikerim 2. Jahrhundert v. Chr. haben als Erste Logarithmen erwähnt. Schon in derAntikenutzten sie Logarithmen zur Basis 2 für ihre Berechnungen. Im 8. Jahrhundert beschrieb der indische MathematikerVirasenaLogarithmen zur Basis 3 und 4. Ab dem 13. Jahrhundert wurden von arabischen Mathematikern ganze logarithmische Tabellenwerke erstellt.

Nicolas Chuquetarbeitete klar die Rechengesetze für Potenzen$a^{n}\cdot a^{m}=a^{n+m}$und$(a^{n})^{m}=a^{n\cdot m}$heraus durch eine gegenüberstellende Anordnung einer arithmetischen und einer geometrischen Reihe.

Der deutsche MathematikerMichael Stifelformulierte ähnlich im Jahr 1544 die Beziehungen$q^{m}\cdot q^{n}=q^{m+n}$und${\tfrac {q^{m}}{q^{n}}}=q^{m-n}$neben anderen Autoren des 16. Jahrhunderts. Die Reduktion von Multiplikation auf Addition steht neben trigonometrischen Additionsformeln am Beginn der Entwicklung der Logarithmen.Stifel ließ nur ganzzahlige Exponenten zu.John Napiers(1550–1617) Idee war dagegen, einenstetigenWertebereich für die Exponenten zuzulassen.

Im 17. Jahrhundert entwickelte der Schweizer UhrmacherJost Bürgi(1552–1632) ein neues System zur Berechnung von Logarithmen, das er 1620 nach langer Arbeit veröffentlichte. Aber schon vorher, im Jahre 1614, veröffentlichte der schottische DenkerJohn Napierein Buch über Logarithmen,das ihn als „Erfinder der Logarithmen “berühmt machte. Ihre Arbeiten und Erkenntnisse über Logarithmen entwickelten Bürgi und Napier jedoch unabhängig voneinander.

Das griechische Wort „Logarithmus “bedeutet auf Deutsch „Verhältniszahl “und stammt von Napier. Es gilt nämlich: Genau dann steht$a$zu$b$im selben Verhältnis wie$c$zu$d$(alsFormel:$a:b=c:d$), wenn die Unterschiede ihrer Logarithmen übereinstimmen (als Formel:$\log(a)-\log(b)=\log(c)-\log(d)$). Erstmals veröffentlicht wurden Logarithmen von diesem unter dem TitelMirifici logarithmorum canonis descriptio,was mitBeschreibung des wunderbaren Kanons der Logarithmenübersetzt werden kann.

Nachdem der Oxforder ProfessorHenry Briggs(1561–1630) sich intensiv mit dieser Schrift beschäftigt hatte, nahm er mit ihrem Autor Kontakt auf und schlug vor, für die Logarithmen die Basis 10 zu verwenden (abgekürzt lg). Diese verbreiteten sich schnell und wurden besonders in der Astronomie geschätzt, was auchPierre-Simon Laplace,im Vergleich zu den vorher benutzten trigonometrischen Tafeln, feststellte:

„L’invention des logarithmes, en réduisant le temps passé aux calculs de quelques mois à quelques jours, double pour ainsi dire la vie des astronomes. “

„Dadurch, dass die für Rechnungen benötigte Zeit von einigen Monaten auf einige Tage reduziert wurde, hat die Erfindung der Logarithmen sozusagen die Lebenszeit eines Astronomen verdoppelt. “

Wird dieEulersche Zahl$\mathrm {e}$– die im Jahre 1728 vonLeonhard Euler(1707–1783) bestimmt und erstmals 1742 veröffentlicht wurde – als Basis des Logarithmus verwendet, so nennt man ihn dennatürlichen Logarithmus.Der natürliche Logarithmus wird dabei durch „ln “abgekürzt.

Mit den Logarithmen war die mathematische Grundlage für die Weiterentwicklung des mechanischenRechenschiebersgelegt; denn die Funktionsweise des Rechenschiebers basiert auf dem Prinzip der Addition und Subtraktion von Logarithmen.

Logarithmus in Anwendung und Natur

Das Gehäuse einesNautiluszeigt einelogarithmische Spirale

Eine logarithmische Spirale

Ein Rechenschieber

Anwendungen des Logarithmus finden sich vielfach in derWissenschaft,wenn der Wertebereich vieleGrößenordnungenumfasst. Daten werden entweder mit einerlogarithmischen Skaladargestellt, oder es werdenlogarithmisch definierte Größenverwendet, wie zum Beispiel beimpH-Wertoder bei der Empfindlichkeit derSinnesorgane.

In der belebten Natur

In der belebten Natur finden sich zahlreiche Beispielelogarithmischer Spiralen,so z. B. das Wachstum von Schneckenhäusern oder die Anordnung der Kerne auf derSonnenblume.

Schalldruckpegel

DerSchalldruckpegelwird als logarithmisches Maß zur Beschreibung der Stärke eines Schallereignisses verwendet. Dazu wird dieHilfsmaßeinheitDezibel(dB) verwendet.

Helligkeitsempfindung

Auch für die Sinnesempfindung derHelligkeithat sich eine logarithmische Bewertung bewährt (Weber-Fechner-Gesetz), da das menschliche Auge zwischen Dämmerung und hellem Sonnenschein bis zu 10,5 Zehnerpotenzen an physikalischer Leuchtdichte überbrücken kann.

pH-Wert

DerpH-Wertist das Maß für den sauren oder basischen Charakter einer wässrigen Lösung. Anmerkung: In der Chemie werden logarithmische Skalen im Allgemeinen durch ein vorangestelltes p (für Potenz) gekennzeichnet, zum Beispiel beimpK_S- oderpK_B-Wert.

Richterskala

DieRichterskala,die zur Beschreibung von Erdbebenstärken genutzt wird, basiert auf einer deka-logarithmischen Einteilung. Die Erdbebenstärke steigt daher von Stufe zu Stufe exponentiell.

Sternhelligkeiten

Sternhelligkeiten werden in astronomischenGrößenklassenangegeben, die ein logarithmisches Maß der tatsächlichen Strahlungsstärke darstellt.

Rechenschieber

Bevor elektronische Rechenmaschinen zur Verfügung standen, nutzte man dieLogarithmengesetzeaus, umMultiplikationenzuAdditionenundDivisionenzuSubtraktionenzu vereinfachen. Die Berechnung derQuadratwurzelvereinfacht sich auf der Ebene des Logarithmus zu einer Division durch Zwei. Weil der Logarithmus selbst nicht so leicht zu berechnen ist, warenRechenschiebermit ihren logarithmischen Skaleneinteilungen und Logarithmische Rechentafeln (Logarithmentafeln) weit verbreitete Hilfsmittel.

Wachstums- und Zerfallsprozesse

Typische Aufgabenstellungen bei Wachstums- und Zerfallsprozessen lassen sich durch die Umkehrfunktion des Logarithmus – die Exponentialfunktion – modellieren. SieheExponentieller Vorgang,Absorption.

Anzahl der Ziffern einer Zahl

Berechnung der Anzahl der Ziffern, die zur Darstellung einer natürlichen Zahl in einemStellenwertsystembenötigt werden. Um eine natürliche Zahl$n$zur Basis$b$darzustellen, werden$1+\lfloor \log _{b}n\rfloor$Stellen benötigt. DieKlammernbedeuten dabei Abrunden auf die nächste ganze Zahl, die kleiner oder gleich ist.

Zum Beispiel ist$\log _{2}100\approx 6{,}64$.Die obige Formel liefert den Wert 7. Man braucht also 7 Ziffern, um 100 imDualsystemdarzustellen, nämlich$100=1100100_{2}$.Stellt man hingegen 100 imHexadezimalsystemdar, dann benötigt man dazu zwei Stellen, denn$\log _{16}100\approx 1{,}66$.Es ist$100=64_{16}$.

Benfordsches Gesetz

Die Verteilung der Ziffern von Zahlen in empirischen Datensätzen, zum Beispiel ihrer ersten Ziffern, folgt einer logarithmischen Verteilung, demBenfordschen Gesetz.

Informationseinheit

Messung derInformationsmenge;dieInformationstheoriesagt, dass, wenn etwas mitWahrscheinlichkeit$p$auftritt, das Wissen über das tatsächliche Auftreten davon eine Informationsmenge von$\log _{2}{\tfrac {1}{p}}$bit ergibt. Zum Beispiel erhält man beim Ergebnis „Kopf “eines fairenMünzwurfs($p=0{,}5$) die Informationsmenge$\log _{2}2=1$bit, und es genügt einBit,um diese Information zucodieren.

Kryptographie

Derdiskrete Logarithmusist inendlichen Körpernund darauf definiertenelliptischen Kurvenerheblich aufwändiger zu berechnen als seine Umkehrfunktion, diediskrete Exponentialfunktion.Letztere kann daher als sogenannteEinwegfunktionin derKryptografiezurVerschlüsselungangewandt werden.

LogarithmischeZeitskalen

Logarithmische Zeitskalen finden sich in der Geschichte derTechnikebenso wie in dergeologischen Zeitskala.

Intervalle der Musiktheorie

Intervalle haben einen exponentiellen Frequenzverlauf. Das Gehör jedoch empfindet diese als linear. Die Größen von Intervallen werden daher als multiplikative Faktoren auf Frequenzen aufgefasst und als rationale Zahlen oder als Logarithmen angegeben. In diesem Fall wird die Oktave in 1200Centunterteilt. Beispiel:

Intervall	Frequenzverhältnis	Größe
1 Oktave	2	1200 Cent
2 Oktaven	4	2400 Cent
3 Oktaven	8	3600 Cent
…
reine große Terz	5:4	$1200\cdot \log _{2}{\big (}{\tfrac {5}{4}}{\big )}\,{\text{Cent}}\approx 386{,}314\,{\text{Cent}}$
reine Quinte	3:2	$1200\cdot \log _{2}{\big (}{\tfrac {3}{2}}{\big )}\,{\text{Cent}}\approx 701{,}955\,{\text{Cent}}$

Graphische Darstellung von Funktionen

Zur graphischen Darstellung von Funktionen werden speziellemathematische Papiereverwendet, wie beispielsweiseeinfachlogarithmisches Papieroderdoppeltlogarithmisches Papier.

Bezeichnungen

Man schreibt für den Logarithmus von$a$zur Basis$b$

$x=\log _{b}a$

und sagt:„$x$ist der Logarithmus von$a$zur Basis$b$“.$a$heißtNumerusoder veraltet auchLogarithmand. Das Ergebnis$x$des Logarithmierens gibt also an, mit welchem Exponenten man die Basis$b$potenzieren muss, um den Numerus$a$zu erhalten.

Für die Vorkommastellen des Logarithmus wird meist der BegriffCharakteristik(manchmal auchKennzahl) verwendet, seine Nachkommastellen werdenMantissegenannt.

Bedienelemente an einem Taschenrechner. Die TasteLOGsteht herstellerübergreifend für den Logarithmus zur Basis 10,LNberechnet den natürlichen Logarithmus zur Basise.Darüber hinaus ist als zweite Belegung der jeweiligen Tasten die entsprechendeUmkehrfunktionvorgesehen (gelbe Beschriftung jeweils oberhalb), dieExponentialfunktionzur Basis 10 oder e.

Die Schreibweise

$\operatorname {log} _{b}a$

ist das allgemeine mathematische Zeichen für den Logarithmus gemäßDIN 1302.Seltener findet man auch davon abweichende Schreibweisen, wie zum Beispiel${}_{b}\,\!\log a$.

Das Zeichen$\log$ohne eine angegebene Basis wird verwendet, wenn die verwendete Basis keine Rolle spielt, wenn diese getrennt vereinbart wird, aus dem Zusammenhang ersichtlich ist oder aufgrund einer Konvention festgelegt ist. In technischen Anwendungen (so z. B. auf den meisten Taschenrechnern) steht$\log$oft für dendekadischen Logarithmus.In theoretischen Abhandlungen, insbesondere zuzahlentheoretischen Themen,steht$\log$oft für dennatürlichen Logarithmus.

Darüber hinaus sind für den Logarithmus in DIN 1302 je nach Anwendung spezielle Schreibweisen festgelegt:

• $\operatorname {ln} a$–Natürlicher Logarithmus(lateinischlogarithmus naturalis),der Logarithmus zur Basis$\mathrm {e}$,derEulerschen Zahl2,7182818… Er wird im Zusammenhang mitExponentialfunktionenverwendet.
• $\operatorname {lg} a$–Dekadischer Logarithmus,auch alsZehnerlogarithmusoderBriggsscher Logarithmusbezeichnet, der Logarithmus zur Basis 10. Er wird bei numerischen Rechnungen im Dezimalsystem verwendet.
• $\operatorname {lb} a$–Binärer Logarithmus,auch alsZweierlogarithmusbezeichnet, der Logarithmus zur Basis 2. Er wird in der Informatik bei Rechnungen imBinärsystemverwendet. Außerhalb der Norm wird mit gleicher Bedeutung auch$\operatorname {ld} a$–logarithmus dualis– verwendet.

Ein ähnlich aussehendes Funktionszeichen ist$\operatorname {li} a$für denIntegrallogarithmus.Bei dieser Funktion handelt es sich abernichtum eine Logarithmusfunktion.

Definition

Der Logarithmus kann mathematisch stets als eine Schar von Funktionen (deren Parameter mit$b$bezeichnet sei)

$\log _{b}:\mathbb {R} ^{+}\to \mathbb {R}$

aufgefasst werden. Ihre einzelnen Logarithmusfunktionen sind dabei nur unterschiedliche (reelle, aber ungleich null) Vielfache voneinander.

Über den positiven reellen Zahlen kann er auf verschiedene Arten eingeführt werden. Je nach Hintergrund und Intention wird man den einen oder anderen didaktischen Zugang wählen. Die verschiedenen Definitionen des reellen Logarithmus sind dabei untereinanderäquivalentund erfolgen hier mit besonderem Fokus auf den natürlichen Logarithmus, der aus Sicht des Mathematikers aufnatürlicheWeise auftritt, wie bei dem Zugang über dieStammfunktionvon${\tfrac {1}{t}}$erkennbar ist.

Als Umkehrfunktion der Exponentialfunktion

Der Logarithmus zur Basis$b$ist die Umkehrfunktion der allgemeinenExponentialfunktionzur positiven Basis$b\neq 1$:

$x\mapsto b^{x}.$

Die Funktionen$b^{x}$und$\log _{b}x$sind alsoUmkehrfunktionenvoneinander, d. h. Logarithmieren macht Exponenzieren rückgängig und umgekehrt:

$b^{\log _{b}x}=x\quad {\text{und}}\quad \log _{b}(b^{x})=x.$

Der natürliche Logarithmus ergibt sich mit der Basis$b=\mathrm {e}$,wobei

$\mathrm {e} =2{,}718281828459\ldots$

dieEulersche Zahlist.

Als Lösung einer Funktionalgleichung

Die Logarithmusfunktionen sind die nicht-trivialen, stetigen Lösungen$L$derFunktionalgleichung

$L(x\cdot y)=L(x)+L(y).$

Ihre Lösungen erfüllen stets$L(1)=0$und erweisen sich sogar als differenzierbar. Den natürlichen Logarithmus erhält man dann zusammen mit der Zusatzbedingung

$L'(1)=1.$

Die Zusatzbedingung ist einer der Gründe dafür, den so erhaltenen Logarithmus alsnatürlichzu bezeichnen. Wollte man den Logarithmus zu einer anderen Basis$b$über die Zusatzbedingung erhalten, dann müsste man

$L'(1)={\frac {1}{\ln b}}$

fordern und würde wieder den natürlichen Logarithmus benötigen.

Die triviale Lösung obiger Funktionalgleichung ist dieNullfunktion$L(x)=0$,die nicht als Logarithmusfunktion angesehen wird, und die einzige Lösung der Funktionalgleichung, für die auch$L(0)$definiert ist.

Der Logarithmus vermittelt aufgrund obiger Funktionalgleichung daher insbesondere einestrukturerhaltende Abbildungvon den positiven reellen Zahlen mit ihrer multiplikativen Struktur auf die gesamten reellen Zahlen mit deren additiver Struktur. Dies kann man auch explizit als Bedingung fordern und gelangt damit zur Herleitung.

Als Isomorphismus

Die reellwertigen Logarithmen sind genau die stetigenIsomorphismen

$L\colon (\mathbb {R} ^{+}\!,\,\cdot \,)\longrightarrow (\mathbb {R},+)$.

Diese Definition legt die Funktion$L$bis auf eine multiplikative Konstante eindeutig fest.

Der algebraische Zugang betont ebenso wie der Zugang über die Funktionalgleichung die historische Bedeutung des Logarithmus als Rechenhilfe: Er ermöglicht es, eine Multiplikation in eine Addition „umzuwandeln “.

Als Stammfunktion vonfmitf(x)=1/x

Der natürliche Logarithmus als Fläche unter dem Graphen von 1/x

Die Funktion

$L\colon t\mapsto \int _{1}^{t}{\frac {1}{x}}\,\mathrm {d} x$

mit$t>0$ist gerade der natürliche Logarithmus: Es ist$L=\ln$.Zum Logarithmus mit der Basis$b$gelangt man durch Division der Funktion$L$durch die Konstante$L(b)=\ln b$.Als uneigentliches Integral von$f$,oder beliebiger willkürlicher (positiver) unterer Integrationsgrenze, betrachtet, würde man nur noch eine zusätzliche, additive Konstante erhalten, aber immer nur den Logarithmus zur Basis$\mathrm {e}$bekommen.

Als Potenzreihe

Der natürliche Logarithmus kann alsPotenzreihegemäß

$\ln(1+x)=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {x^{k}}{k}}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dotsb$

eingeführt werden. Diese Reihe konvergiert für$|x|<1$und für$x=1$.

Für eine numerische Berechnung des Werts$\ln(1+x)$für$x>1$ist die Beziehung$\ln(1+x)=-\ln {\Bigl (}1-{\frac {x}{1+x}}{\Bigr )}$nützlich.

Anmerkung

Diese Definitionen können auch herangezogen werden, um Logarithmen auf anderen mathematischen Strukturen zu erhalten, wie z. B. auf den komplexen Zahlen. Das setzt voraus, dass in der betreffenden Struktur die zur Definition verwendeten Konzepte existieren.

Um etwa dendiskreten Logarithmusauf einerGruppezu definieren, können Konzepte wie Differentiation/Integration nicht herangezogen werden, weil sie dort gar nicht existieren. (Die Definition geschieht dort als Umkehrung der Potenzierung mit ganzen Exponenten, die wiederum aus mehrfachem Anwenden dereinenVerknüpfung der Gruppe definiert ist.)

Rechenregeln und grundlegende Eigenschaften

Logarithmengesetze

Im Folgenden wird stets vorausgesetzt, dass die Variablen$x,y,x_{i},r,a,b$von Null verschieden sind; im Falle des reellen Logarithmus werden die Zahlen sogar als positiv vorausgesetzt. Die Basen$a,b$des Logarithmus dürfen ferner nicht 1 sein.

Produkte

Für das Rechnen mit Logarithmen von Produkten steht die hilfreiche Rechenregel

$\log _{b}(x\cdot y)=\log _{b}x+\log _{b}y$

zur Verfügung; oder allgemeiner:

$\log _{b}(x_{1}x_{2}\dotsm x_{n})=\log _{b}x_{1}+\log _{b}x_{2}+\dotsb +\log _{b}x_{n}$

bzw.

$\log _{b}\prod _{i=1}^{n}x_{i}=\sum _{i=1}^{n}\log _{b}x_{i}.$

Der Logarithmus eines Produkts ist die Summe der Logarithmen der Faktoren.

Quotienten

Die Quotienten leiten sich direkt aus den Logarithmen von Produkten ab. Hier sei nur der einfache Fall

$\log _{b}{\frac {x}{y}}=\log _{b}x-\log _{b}y$

angegeben. Der Logarithmus eines Quotienten ist der Logarithmus des Zählers$x$minus den Logarithmus des Nenners$y$.

Insbesondere ergibt sich daraus (da$\log 1=0$):

$\log _{b}{\frac {1}{x}}=-\log _{b}x$

Allgemeiner ergibt sich direkt aus der obigen Quotientenregel dasReziprozitätsgesetz:

$\log _{b}{\frac {x}{y}}=-\log _{b}{\frac {y}{x}}$

Summen und Differenzen

Aus der Formel für Produkte kann eine Formel für Logarithmen von Summen (und Differenzen) wie$x+y$hergeleitet werden, indem$x$ausgeklammert wird:

$x+y=x\left(1+{\frac {y}{x}}\right).$

Damit ergibt sich die „Regel “

$\log _{b}(x+y)=\log _{b}x+\log _{b}\left(1+{\frac {y}{x}}\right).$

Potenzen

Für Potenzen mit reellem Exponent$r$gilt die Regel

$\log _{b}\left(x^{r}\right)=r\log _{b}x.$

Der Logarithmus einer Potenz ist also das Produkt aus dem Exponenten mit dem Logarithmus der Basis.

Auch daraus lässt sich für$r=-1$

$\log _{b}{\frac {1}{x}}=-\log _{b}x$

ermitteln.

Der Logarithmus einesStammbruchs${\tfrac {1}{x}}$ist der negative Logarithmus des Nenners$x$.

Diese Rechenregeln lassen sich von denPotenzgesetzenableiten.

Wurzeln

Dieses Dreieck zeigt die Beziehungen zwischen der Potenz, der Wurzel und dem Logarithmus. Geht man von den Ecken in die Richtung der Pfeile, wird man zu einem Ergebnis geleitet

Da Wurzeln nichts anderes als Potenzen mit gebrochenem Exponenten sind, ergibt sich nach der oben angegebenen Potenzregel des Logarithmus die Rechenregel

$\log _{b}{\sqrt[{n}]{x}}=\log _{b}\left(x^{\frac {1}{n}}\right)={\frac {1}{n}}\log _{b}x.$

Basisumrechnung

Um Logarithmen zur Basis$b\neq 1$mithilfe von Logarithmen einer beliebigen Basis$a\neq 1$zu berechnen, verwendet man den Zusammenhang

$\;\;\;\log _{b}x={\frac {\log _{a}x}{\log _{a}b}}$,

denn mit$\;\;y=\log _{b}x\;\;$gelten die Umformungen

${\begin{aligned}b^{y}&=x\\\log _{a}b^{y}&=\log _{a}x\\y\log _{a}b&=\log _{a}x\\y&={\frac {\log _{a}x}{\log _{a}b}}\end{aligned}}$

Damit sieht man, dass sich Logarithmen zu verschiedenen Basen nur um einen konstanten Faktor voneinander unterscheiden. Die meisten Tabellenwerke stellen Logarithmen nur zur Basis 10 zur Verfügung, Taschenrechner auch zur Basis$\mathrm {e}$(den natürlichen Logarithmus). Mit der obigen Formel lassen sich daraus Logarithmen zu einer beliebigen Basis berechnen.

Ein prominenter Spezialfall, der sich für$\;a\neq 1\land b\neq 1\;$aus obiger Formel ergibt, ist

$\log _{a}b={\frac {1}{\log _{b}a}}\quad$oder$\quad \log _{a}b\cdot \log _{b}a=1$.

Beispiel

$\log _{10}8={\frac {\log _{2}8}{\log _{2}10}}={\frac {\ln 8}{\ln 10}}$

für beliebige positive Zahlen$x$ist${\frac {\ln x}{\log _{10}x}}=\ln 10\approx 2{,}302585$

Beispiel für den Kehrwert der Basis

$\log _{a^{-1}}x=-\log _{a}x$.

Nichtpositive Zahlen

In denreellen Zahlenist der Logarithmus für nichtpositive Zahlen, alsoNullundnegative Zahlen,nicht definiert. Allerdings erfüllt$\log _{b}|x|$obige Funktionalgleichung für$L(\cdot )$,solange nur$x,y\not =0$ist, da diese dort eine Unstetigkeitsstelle hat. Ansonsten würde für$x=0$ja für alle$y$stets$0=L(y)$folgen, wenn man ihre Gültigkeit auf ganz$\mathbb {R}$,also auch bei$x=0$,verlangen würde.

• $x=\log _{b}0$müsste dann$0=b^{x}$bedeuten. Ist$b$ungleich Null, ist dies jedoch für kein reelles$x$lösbar.
• (als Beispiel die negative Zahl −1)$x=\log _{b}(-1)$müsste dann$-1=b^{x}$bedeuten. Dies ist ebenfalls für keine reelle Zahl$x$möglich, wenn$b$größer Null ist.

In derFunktionentheorie,in der Funktionen vonkomplexen Zahlenbetrachtet werden, kann man den Logarithmus auch für negative Zahlen definieren (sieheKomplexer Logarithmus), allerdings gelten dann einige der Rechenregeln nicht mehr. Auch in diesem Zusammenhang ist 0 keineisolierte Singularität,sondern einVerzweigungspunkt.

Ableitung und Integral

Die natürliche Logarithmusfunktion ist dieUmkehrfunktionderExponentialfunktion.Daher erhält man dieAbleitungdes natürlichen Logarithmus einfach durch Anwendung derUmkehrregel(sieheBeispiel dort). Es ergibt sich

${\frac {\mathrm {d} }{\mathrm {d} x}}\ln(x)={\frac {1}{x}}$

fürpositives$x$.Fürnegatives$x$folgt daraus (wegen$-x>0$und unter Anwendung derKettenregel)

${\frac {\mathrm {d} }{\mathrm {d} x}}\ln(-x)={\frac {1}{-x}}\cdot (-1)={\frac {1}{x}}$

und wegen$|x|={\begin{cases}x,&{\text{für }}x>0\\-x,&{\text{für }}x<0\end{cases}}$lässt sich beides zu

$\forall \ x\neq 0\colon {\frac {\mathrm {d} }{\mathrm {d} x}}\ln |x|={\frac {1}{x}}$

zusammenfassen. Für allgemeine Logarithmen gilt:

${\frac {\mathrm {d} }{\mathrm {d} x}}\log _{b}|x|={\frac {1}{x\ln b}}.$

Für alle reellen$x\neq 0$ist

$\int _{-1}^{x}{{\frac {1}{t}}\,\mathrm {d} t}=\ln |x|,$

wobei für positives$x$(wenn also über den Pol bei$t=0$integriert wird) derHauptwertdes Integrals zu nehmen ist.

DieStammfunktion(auch bekannt alsunbestimmtes Integral) des natürlichen Logarithmus lässt sich durchpartielle Integrationgewinnen:

${\begin{aligned}\int {\ln |x|\,\mathrm {d} x}&=\int 1\cdot \ln |x|\,\mathrm {d} x\\&=\int {\frac {\mathrm {d} }{\mathrm {d} x}}x\cdot \ln |x|\,\mathrm {d} x\\&=x\ln |x|-\int x{\frac {1}{x}}\,\mathrm {d} x\\&=x\ln |x|\;-x+C.\end{aligned}}$

Ist bei einem bestimmten Integral des natürlichen Logarithmus eine der Grenzen Null, so kann dieRegel von de L’Hospitalangewendet werden.

Beispiel

$\int _{0}^{1}{\ln x\,\mathrm {d} x}=[x\ln {x}-x]_{0}^{1}=-1,$

da

${\begin{aligned}\lim _{x\to 0^{+}}x\ln x&=\lim _{x\to 0^{+}}{\frac {\ln x}{1/x}}\\&=\lim _{x\to 0^{+}}{\frac {1/x}{-1/x^{2}}}\\&=\lim _{x\to 0^{+}}-x\\&=0.\end{aligned}}$

Kurvendiskussion

• Definitionsmenge:$\mathbb {R} ^{+}={\mathopen {]}}0,\infty {\mathclose {[}}$
• Wertemenge:$\mathbb {R}$
• Nullstellenmengebzw. Kurvenschnittpunkte mit denKoordinatenachsen:{1} bzw. (1|0)
• AsymptotischesVerhalten:

$\lim _{x\to 0^{+}}\log _{b}x={\begin{cases}-\infty,&{\text{wenn }}b>1\\+\infty,&{\text{wenn }}b<1\end{cases}}$

$\lim _{x\to \infty }\log _{b}x={\begin{cases}+\infty,&{\text{wenn }}b>1\\-\infty,&{\text{wenn }}b<1\end{cases}}$

• ErsteAbleitung:

$(\log _{b}|x|)'={\frac {1}{x\ln b}}$

• Extrempunkte:keine
• Wendepunkte:keine
• Monotonie:streng monoton steigend/wachsend (wenn$b>1$) bzw. fallend (wenn$b<1$)
• Flächeninhaltder Fläche zwischen Kurve, y-Achse und x-Achse bis x ≤ 1:${\frac {1}{|\ln b|}}$
• Krümmungsextremum bei$x_{k}={\frac {1}{{\sqrt {2}}|\ln b|}}$mit$\kappa (x_{k})=-{\frac {2\ln b}{3{\sqrt {3}}}}$

Natürlicher Logarithmus

Der Logarithmus zur Basis$\mathrm {e}$(derEulerschen Zahl) wird auch alsnatürlicher Logarithmusbezeichnet und mit „ln “oder oft auch „log “(ohneTiefstellung) abgekürzt:

Wenn$y=\mathrm {e} ^{x}$,dann ist$x=\log _{\mathrm {e} }y=\ln y$

– oder einfacher formuliert:$\ln(\mathrm {e} ^{x})=x$

Die Zahl$\mathrm {e}$ist z. B. dadurch ausgezeichnet (und könnte auch so definiert werden), dass dieExponentialfunktion$\mathrm {e} ^{x}$sich bei Ableitung nach$x$wieder selbst reproduziert, als Formel:

${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {e} ^{x}=\mathrm {e} ^{x}.$

Der Begriffnatürlicher Logarithmuswurde gewählt, weil sowohl die Exponentialfunktion als auch der Logarithmus zur Basis$\mathrm {e}$in vielen Zusammenhängen (Integralrechnung,Differentialrechnung,Komplexe Zahlen,Trigonometrie) auf natürliche Weise ohne Vorfaktoren auftreten. Insbesondere lässt sich der natürliche Logarithmus sehr einfach integrieren und differenzieren.

Der natürliche Logarithmus$\ln$ist eine Stammfunktion$F$der Kehrwertfunktion$f$mit$f(x)=x^{-1}={\tfrac {1}{x}}$,nämlich genau die mit$F(1)=0$.

Berechnung des Logarithmus

Die Berechnung eines Logarithmus ist prinzipiell kompliziert. Sie lässt sich „mit Papier und Bleistift “nur durch die vielfache Wiederholung bestimmter Rechenvorgänge erreichen, wobei das Ergebnis des gerade ausgeführten Schrittes als Ausgangsbasis für den nächsten Rechenschritt verwendet wird (Iterative Vorgehensweise). Meist kann man sich dem Wert nur annähern(Approximation). Dazu gibt es verschiedene mögliche Vorgehensweisen, von denen einige im Folgenden dargestellt sind. Anfangs ist das Ergebnis dieser Teilschritte jeweils relativ weit entfernt von dem korrekten Ergebnis, wird aber bei jedem weiteren Rechenschritt genauer: eskonvergiertzu dem korrekten Ergebnis. Solche iterativen Rechenoperationen sind sehr gut geeignet, um sie automatisch von einemTaschenrechneroderComputerausführen zu lassen, wo lediglich eine Taste gedrückt werden muss (falls auf dem Gerät vorgesehen), um den Logarithmus der eingegebenen Zahl zu einer festgelegten Basis (meist derEulerschen Zahle= 2,718… oder der Zahl 10) zu berechnen. Die folgenden Rechenbeispiele sind jeweils nur zur Berechnung des Logarithmus einer beliebigen Zahl zur Basise (natürlicher Logarithmus)oder 2 geeignet.

Potenzreihe

Illustration der ersten Teilsummen der vonNicolaus Mercatorentdeckten Reihendarstellung des natürlichen Logarithmus; die Reihe konvergiert nur im nicht-schraffierten Bereich

Reihe über den Logarithmus Naturalis

Die Potenzreihenentwicklung des natürlichen Logarithmus um den Entwicklungspunkt 1 ergibt sich für$-1<x\leq 1$als

${\begin{aligned}\ln(1+x)&=-\sum _{k=0}^{\infty }{\frac {(-x)^{k+1}}{k+1}}\\&=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}\pm \dotsb \\&\qquad \dotsb +(-1)^{n+1}{\frac {x^{n}}{n}}\;+\;R_{n+1}(x)\,.\end{aligned}}$

Sie konvergiert nicht sonderlich schnell an den Rändern des Konvergenzintervalls, das Restglied der$n$-ten Partialsumme hat die Größe

$|R_{n+1}(x)|\leq {\frac {|x|^{n+1}}{(n+1)(1-|x|)}}.$

Mit Hilfe der Formel$\ln(x)=m\ln(2)+\ln(2^{-m}x)$kann man die Berechnung des Logarithmus für beliebige$x$auf die für Werte im Intervall${\big [}{\tfrac {2}{3}},{\tfrac {4}{3}}{\big ]}$reduzieren, d. h., man findet immer$m$und$y$mit$2^{-m}x=1+y$und$|y|\leq {\tfrac {1}{3}}$

Illustration der Konvergenz der nebenstehenden artanh-Entwicklung für unterschiedliche Anzahl von Summanden

Reihe über den Areatangens Hyperbolicus

Mehr Flexibilität in der Reduktion auf Zahlen nahe 1 und eine Halbierung des Berechnungsaufwandes bietet folgendeReihendarstellung,die auf der Potenzreihenentwicklung desAreatangens hyperbolicus $\operatorname {artanh}$  beruht,

${\begin{aligned}\ln x&=2\operatorname {artanh} {\frac {x-1}{x+1}}\\&=\sum _{k=0}^{\infty }{\frac {2}{2k+1}}\cdot \left({\frac {x-1}{x+1}}\right)^{2k+1}\\&=\sum _{k=0}^{n}{\frac {2}{2k+1}}\cdot \left({\frac {x-1}{x+1}}\right)^{2k+1}\!\!+\,\,R_{n+1}(x)\end{aligned}}$

mit der Restgliedabschätzung

$|R_{n+1}(x)|\leq {\frac {(x-1)^{2}}{2(2n+3)\,|x|}}\left|{\frac {x-1}{x+1}}\right|^{2n+1}.$

Die Reihe konvergiert für$x>0$,zeigt für$x$und${\tfrac {1}{x}}$ähnliches Konvergenzverhalten und konvergiert umso besser, je näher$x$bei 1 liegt. Um dies zu erreichen, verwendet man wieder

$\ln x=2m\ln({\sqrt {2}})+\ln(2^{-m}x).$

Durch Wahl einer geeigneten ganzen Zahl$m$kann man immer erreichen, dass gilt ${\tfrac {1}{\sqrt {2}}}\leq 2^{-m}x\leq {\sqrt {2}}$ und erhöht damit die Konvergenzgeschwindigkeit der Reihe, die man jetzt für$2^{-m}x$berechnet. Allerdings muss man zusätzlich noch eine Näherung für$\ln {\sqrt {2}}={\tfrac {1}{2}}\ln 2$berechnen, was über die gleiche Reihe erfolgt. Eine solche Transformation auf ein Intervall${\big [}{\tfrac {1}{b}},b{\big ]}$durch Skalierung von$x$mit$b^{2m}$ist auch für andere Werte von$b$möglich, durch die besonders einfache Handhabung der2in binär dargestellten Zahlen wird selten ein anderer Faktor verwendet.

Kettenbruch

Die oben angegebene Potenzreihe von$\ln(1+x)$lässt sich auch alsKettenbruchdarstellen:

$\ln(1+x)={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+\ddots }}}}}}}}$

Additive Zerlegung

Der natürliche Logarithmus  $\ln$  steht, wie im obigen Abschnitt erwähnt, mit demAreatangens hyperbolicus $\operatorname {artanh}$  per

$\ln x=2\operatorname {artanh} {\frac {x-1}{x+1}}\qquad \,(0<x)$

in Beziehung, was nach der anderen Seite aufgelöst

$\operatorname {artanh} u={\frac {1}{2}}\ln {\frac {1+u}{1-u}}\qquad (-1<u<1)$

ergibt.

Die Logarithmen der positiv-ganzzahligen Numeri lassen sich damit in aufsteigenden Einerstufen der Form

${\begin{aligned}\ln(n+1)&=\ln n+\ln {\frac {n+1}{n}}=\ln n+2\operatorname {artanh} {\frac {1}{2n+1}}\\&=2\sum _{\nu =1}^{n}\operatorname {artanh} {\frac {1}{2\nu +1}}\end{aligned}}$

darstellen und ausrechnen. Dabei verbessert sich das Konvergenzverhalten derTaylorreihe

$\operatorname {artanh} u=\sum _{k=0}^{\infty }{\frac {u^{2k+1}}{2k+1}}=u+{\frac {1}{3}}u^{3}+{\frac {1}{5}}u^{5}+{\frac {1}{7}}u^{7}+\ldots$

geringfügig mit wachsendem$n.$

Mithilfe desAdditionstheorems

$\operatorname {artanh} u+\operatorname {artanh} v=\operatorname {artanh} {\frac {u+v}{1+uv}}$

lässt sich  $\operatorname {artanh}$  und damit auch  $\ln$  additiv zerlegen. So ergeben sich beispielsweise die folgenden Identitäten für die natürlichen Logarithmen der ersten Primzahlen. Dabei werde der Übersichtlichkeit halber das Additionstheorem alsGruppengesetz$\oplus$

$u\oplus v:=\tanh(\operatorname {artanh} u+\operatorname {artanh} v)={\frac {u+v}{1+uv}},$

sowie seine$n$-facheVervielfältigung als

$n\!\odot \!u:=\underbrace {u\oplus u\oplus \dotsb \oplus u} _{n{\text{-mal}}}=\bigoplus _{\nu =1}^{n}u$

formuliert.

$\tanh \left({\tfrac {1}{2}}\ln 2\right)$	$={\tfrac {1}{3}}$	$=2\!\odot \!{\tfrac {1}{7}}\;\oplus \;{\tfrac {1}{17}}$	$=\;\,7\!\odot \!{\tfrac {1}{19}}\;\ominus \;\;\,2\!\odot \!{\tfrac {1}{49}}\;\oplus \;3\!\odot \!{\tfrac {1}{161}},$
$\tanh \left({\tfrac {1}{2}}\ln 3\right)$	$={\tfrac {1}{2}}$	$=3\!\odot \!{\tfrac {1}{7}}\;\oplus \;2\!\odot \!{\tfrac {1}{17}}$	$=11\!\odot \!{\tfrac {1}{31}}\;\oplus \;\;\,8\!\odot \!{\tfrac {1}{49}}\;\oplus \;5\!\odot \!{\tfrac {1}{161}},$
$\tanh \left({\tfrac {1}{2}}\ln 5\right)$	$={\tfrac {2}{3}}$	$=4\!\odot \!{\tfrac {1}{5}}\;\ominus \;{\tfrac {1}{161}}$	$=16\!\odot \!{\tfrac {1}{31}}\;\oplus \;12\!\odot \!{\tfrac {1}{49}}\;\oplus \;7\!\odot \!{\tfrac {1}{161}},$
$\tanh \left({\tfrac {1}{2}}\ln 7\right)$	$={\tfrac {3}{4}}$	$=3\!\odot \!{\tfrac {1}{3}}\;\ominus \;{\tfrac {1}{15}}$	$=14\!\odot \!{\tfrac {1}{15}}\;\oplus \;\;\,6\!\odot \!{\tfrac {1}{97}}\;\ominus \;3\!\odot \!{\tfrac {1}{127}}$sowie
$\tanh \left({\tfrac {1}{2}}\ln 11\right)$	$={\tfrac {5}{6}}$	$=2\!\odot \!{\tfrac {1}{2}}\;\oplus \;{\tfrac {1}{10}}$	$=24\!\odot \!{\tfrac {1}{23}}\;\oplus \;11\!\odot \!{\tfrac {1}{65}}\;\ominus \;7\!\odot \!{\tfrac {1}{485}}.$

Für die praktische Rechnung sind Zerlegungen bevorzugt, deren Summanden eine Eins im Zähler haben. Wie beimArkustangensbleiben bei der Verdoppelung

${\tfrac {1}{n}}=2\!\odot \!{\tfrac {1}{2n}}\;\oplus \;{\tfrac {1}{4n^{3}-3n}}$

die Einsen im Zähler erhalten.

Grenzwerte nach Hurwitz

Für den natürlichen Logarithmus gelten die Grenzwerte

$\ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)$

sowie gleichbedeutend damit

$\ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}=\lim _{h\to 0}\int _{1}^{x}{\frac {1}{t^{1-h}}}\,\mathrm {d} t$

die man leicht mit derRegel von de L’Hospitalbestätigt.

Hierauf basieren die vonAdolf Hurwitzfür den natürlichen Logarithmus angegebenen Grenzwerte der Folgen$a_{n}$bzw.$b_{n}$,die über

${\begin{aligned}a_{n}&=2^{n}(x_{n}-1)\\b_{n}&=2^{n}\left(1-{\frac {1}{x_{n}}}\right),\end{aligned}}$

wobei

$x_{n+1}={\sqrt {x_{n}}}\quad {\text{mit}}\quad x_{0}=x$

definiert sind. Wegen$1-{\tfrac {1}{x}}\leq b_{n}\leq a_{n}<x-1$und weil$a_{n}$monoton fallend und$b_{n}$monoton wachsend ist, folgt die Konvergenz dieser beiden Folgen. Aufgrund von$a_{n}=b_{n}x_{n}$und$x_{n}\rightarrow 1$ergibt sich die Gleichheit der beiden Grenzwerte:

$\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }b_{n}=\ln x.$

Für eine praktische Berechnung von ln$x$sind diese Grenzwerte wegen der auftretendenAuslöschungjedoch nicht gut geeignet.

Berechnung einzelner Binärziffern

Eine weitere Möglichkeit zur Berechnung des Logarithmus besteht darin, nacheinander die Ziffern der Binärdarstellung des Logarithmus zur Basis 2 zu bestimmen. Dieses Verfahren ist besonders einfach auf Rechenwerken zu implementieren, da es aufwändige Divisionen vermeidet und auch leicht inFestkomma-Arithmetikumsetzbar ist.

Zunächst werden die Vorkommastellen des Zweierlogarithmus (immer imDualsystem) durch Abzählen der Vorkommastellen der Zahl$x$bestimmt und$x$durchSchiebenauf Werte zwischen 1 und 2 normiert.

Der Logarithmus von$x$hat danach die Darstellung

${\begin{aligned}\log _{2}(x)&=0,b_{1}b_{2}b_{3}\cdots =\sum _{k>0}b_{k}2^{-k}{\text{ mit }}b_{k}\in \{0,1\}\\\log _{2}(x^{2})&=b_{1},b_{2}b_{3}\cdots \qquad {\text{ wegen }}\quad \log(x^{2})=2\log x.\end{aligned}}$

Quadrieren von$x$schiebt den Logarithmus also um eine Binärstelle nach links, wodurch die Vorkommastelle möglicherweise Eins wird. Dies ist dann der Fall, wenn$x^{2}\geq 2$ist. In diesem Falle wird$x$durch Division durch 2 wieder normiert, was keinen Einfluss auf die verbleibenden Nachkommastellen hat. Damit ergibt sich die folgende Skizze des Verfahrens:

INPUT 1 ≤ x < 2
OUTPUT Nachkommastellen bider Binärdarstellung von log2(x)

i ← 0
LOOP
i ← i + 1
x ← x2
IF x ≥ 2 THEN
x ← x / 2
bi← 1
ELSE
bi← 0
END IF
END LOOP

Analogrechner

VereinfachtesSchaltbildeines Logarithmierers

Zur Berechnung des Logarithmus mithilfe einesAnalogrechners– also etwa der Erzeugung einer elektrischenAusgangsspannung$U_{\text{a}}$,die den Logarithmus des Nennwerts der Eingangsspannung$U_{\text{e}}$annimmt – kann man sich den exponentiellen Verlauf derStrom-Spannungs-KennlinieeinerDiodezunutze machen. Die nebenstehende Skizze zeigt den prinzipiellen Aufbau eines Logarithmierers mit einemOperationsverstärker,einer Diode$D$und einemWiderstand$R$.

Komplexer Logarithmus

Riemannsche Flächeder komplexen Logarithmus-Funktion: Die Blätter spiegeln die Mehrdeutigkeit des Logarithmus wider, die aus der Periodizität seiner Umkehrfunktion, der Exponentialfunktion, folgt.

Hauptwert$\ln z$des Logarithmus

Analog zur reellen Definition heißt jede komplexe Zahl$w$,welche die Gleichung

$\mathrm {e} ^{w}=z$

erfüllt, einnatürlicher Logarithmusvon$z$.Für jedes$z\in \mathbb {C} \setminus \{0\}$existiert ein solches$w$,das jedoch im Unterschied zum reellen Logarithmus wegen

$\mathrm {e} ^{2k\pi \mathrm {i} }=1,\quad k\in \mathbb {Z}$,

nicht eindeutig bestimmt ist. Hat man also einen Logarithmus$w$von$z$gefunden, so ist damit auch

$w'=\,\!w+2k\pi \mathrm {i}$

mit jeder ganzen Zahl$k$ein Logarithmus von$z$,denn es gilt

$\mathrm {e} ^{w'}=\mathrm {e} ^{w+2k\pi \mathrm {i} }=\mathrm {e} ^{w}\cdot \mathrm {e} ^{2k\pi \mathrm {i} }=\mathrm {e} ^{w}\cdot 1=\mathrm {e} ^{w}=z$.

Um Eindeutigkeit zu erreichen, wählt man aus den möglichen Werten für$w$solche Werte aus, die in einem geeigneten Streifen der komplexen Zahlenebene liegen. Man kann z. B. den Streifen

$\left\{w\in \mathbb {C}:-\pi <\operatorname {Im} \,w\leq \pi \right\}$

verwenden. Ein Wert$w$aus diesem Streifen heißtHauptwert(englischprincipal value) des Logarithmus, und man schreibt$w=\ln z$. Stellt man$z=|z|\cdot \mathrm {e} ^{\mathrm {i} \arg z}$inPolarformdar, so erhält man eine einfache Darstellung desk-ten Zweigesder Logarithmusfunktion:

$w=\ln |z|+\mathrm {i} \left(\arg z+2k\pi \right),\quad k\in \mathbb {Z}$

mit derArgument-Funktion$\arg$.Im Summanden$\ln |z|$wird der bereits oben definierte reelle Logarithmus$\ln$verwendet. Für$k=0$erhält man denHauptzweigdes komplexen Logarithmus zurück:

$\ln z=\ln |z|+\mathrm {i} \arg z$.

$\ln$ist nicht stetig auf$\mathbb {C} \setminus \{0\}$.Entfernt man jedoch die negative reelle Achse, so ist$\ln$auf dem Gebiet

$\mathbb {C} \setminus \{x\in \mathbb {R}:x\leq 0\}$

stetig und sogarholomorph.

Zur Beachtung

Für den Hauptzweig des komplexen Logarithmus$\ln$gelten nicht alle der weiter oben angeführtenRechenregeln für die reelle Logarithmusfunktion.Sie gelten nur${\text{mod }}2\pi \mathrm {i}$. Diese Mehrdeutigkeit ist eine direkte Folge aus der Periodizität seiner Umkehrfunktion, der komplexen Exponentialfunktion. Der Vergleich von

$\ln(-1+\mathrm {i} )+\ln(-1+\mathrm {i} )={\bigl (}\ln {\sqrt {2}}+{\frac {3\pi }{4}}\mathrm {i} {\bigr )}+{\bigl (}\ln {\sqrt {2}}+{\frac {3\pi }{4}}\mathrm {i} {\bigr )}=\ln 2+{\frac {3\pi }{2}}\mathrm {i}$

mit

$\ln {\bigl (}(-1+\mathrm {i} )(-1+\mathrm {i} ){\bigr )}=\ln(-2\mathrm {i} )=\ln 2-{\frac {\pi }{2}}\mathrm {i}$

zeigt, dass

$\ln x+\ln y=\ln(x\cdot y)$

nicht für alle von$0$verschiedenen komplexen Zahlen$x$und$y$richtig ist. Auch die Gleichung

$y\cdot \ln x=\ln {x^{y}}$

ist nicht immer erfüllt, wie das Gegenbeispiel

$2\pi \mathrm {i} \ln \mathrm {e} =2\pi \mathrm {i} \;\neq \;0=\ln 1=\ln(\mathrm {e} ^{2\pi \mathrm {i} })$

beweist.

• Grafische Darstellung des komplexen Logarithmus
• 
  Betrag von$\ln z$
• 
  Realteil von$\ln z$
• 
  Imaginärteil von$\ln z$

Mit dem oben definierten Hauptzweig des komplexen Logarithmus kann man den Logarithmus von negativen reellen Zahlen erklären:

$\ln(-x)=\ln \left\vert -x\right\vert +\mathrm {i} \arg(-x)=\ln x+\mathrm {i} \pi,\quad x\in \mathbb {R} ^{+}\.$

Das setzt voraus, dass dieArgument-Funktion$\arg$negativen reellen Zahlen den Wert$\pi$zuweist.

Diese Betrachtungen zeigen, dass die Mehrdeutigkeit des komplexen Logarithmus letztlich auf die Mehrdeutigkeit derArgument-Funktionzurückzuführen ist.

Diskrete Logarithmen

→Hauptartikel:Diskreter Logarithmus

Diskrete Logarithmen sind Lösungen von Gleichungen der Form

$a^{n}=\underbrace {a\circ a\circ \dotsb \circ a} _{n{\text{-mal}}}=b$

über einer endlichenzyklischen Gruppe$(G,\circ )=\langle a\rangle$. Der diskrete Logarithmus$x$von$b$zur Basis$a$istmoduloderGruppenordnungvon$G$eindeutig bestimmt und existiert – da$a$ein Erzeuger der Gruppe ist – für alle Elemente der Gruppe.

Diskrete Logarithmen sind im Sinne derKomplexitätstheoriefür viele Gruppen aufwändig zu berechnen und finden Anwendung in derKryptographie,etwa in aufelliptischen Kurven basierenden Kryptosystemen.

Beispiel:

$2^{x}{\bmod {1}}1=5$

hat als Lösung den Wert 4, denn es gilt 2⁴= 16, und 16 lässt den Rest 5 beiDivision mit Restdurch 11. Die Lösung ist eindeutig modulo 10, also modulo der Gruppenordnung von$(\mathbb {Z} \,/\,11\,\mathbb {Z} )^{\times }$.Dementsprechend ist mit$x$auch$x\pm 10$eine Lösung der Kongruenz.

Siehe auch

• Exponentialfunktion
• Eulersche Zahl
• Iterierter Logarithmus
• Logarithmische Spirale
• Kettenlogarithmus
• Logarithmenpapier
• Matrixlogarithmus
• Verallgemeinerter Logarithmus

Literatur

• Charles Naux:Histoire des Logarithmes de Neper a Euler.Tome I, II. Blanchard, Paris 1966, 1971.
• Wolfgang Walter:Analysis I. Grundwissen Mathematik.Band 3. Springer, Berlin 1985,ISBN 3-540-12780-1.
• Klaus Jänich:Funktionentheorie. Eine Einführung.Springer, Berlin 2004,ISBN 3-540-20392-3.
• I. N. Bronstein,K. A. Semendjajew,G. Musiol, H. Mühlig (Hrsg.):Taschenbuch der Mathematik.10., überarbeitete Auflage. Europa-Lehrmittel, Haan-Gruiten 2016,ISBN 978-3-8085-5790-7.
• Ernst Hairer,Gerhard Wanner:Analysis in historischer Entwicklung.Springer-Verlag, Berlin / Heidelberg 2011,ISBN 978-3-642-13766-2.

Weblinks

Wikibooks:${\color {BlueViolet}{\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$Mathematik für die Schule– Logarithmus

Wikibooks: Logarithmengesetze– Lern- und Lehrmaterialien

Wiktionary: Logarithmus– Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Eric W. Weisstein:Logarithm.In:MathWorld(englisch).
• Logarithmen
• Logarithmen und Logarithmusgesetze.(Onlinekurs, Übungen, Applets und Links)