Differentialrechnung
DieDifferential-oderDifferenzialrechnungist ein wesentlicher Bestandteil derAnalysisund damit ein Gebiet derMathematik.Zentrales Thema der Differentialrechnung ist die Berechnung lokaler Veränderungen vonFunktionen.Während einestetige Funktionihren Eingabewerten kontinuierlich gewisse Ausgangswerte zuordnet, wird durch die Differentialrechnung ermittelt, wie stark sich die Ausgabewerte nach sehr kleinen Veränderungen der Eingabewerte ändern. Sie ist eng verwandt mit derIntegralrechnung,mit der sie gemeinsam unter der BezeichnungInfinitesimalrechnungzusammengefasst wird.
DieAbleitungeiner Funktion dient der Darstellung lokaler Veränderungen einer Funktion und ist gleichzeitig Grundbegriff der Differentialrechnung. Anstatt von der Ableitung spricht man auch vomDifferentialquotienten,dessen geometrische Entsprechung dieTangentensteigungist. Die Ableitung ist nach der Vorstellung vonLeibnizderProportionalitätsfaktorzwischeninfinitesimalenÄnderungen des Eingabewertes und den daraus resultierenden, ebenfallsinfinitesimalenÄnderungen des Funktionswertes. Eine Funktion wird alsdifferenzierbarbezeichnet, wenn ein solcher Proportionalitätsfaktor existiert.Äquivalentwird die Ableitung in einem Punkt als die Steigung derjenigenlinearen Funktiondefiniert, die unter allen linearen Funktionen die Änderung der Funktion am betrachteten Punkt lokal am bestenapproximiert.Entsprechend wird mit der Ableitung in dem Punkt eine lineare Näherung der Funktion gewonnen. DieLinearisierungeiner möglicherweise komplizierten Funktion hat den Vorteil, dass eine einfacher behandelbare Funktion entsteht als die ursprüngliche Funktion oder überhaupt erst eine Handhabbarkeit.
In vielen Fällen ist die Differentialrechnung ein unverzichtbares Hilfsmittel zur Bildungmathematischer Modelle,die die Wirklichkeit möglichst genau abbilden sollen, sowie zu deren nachfolgender Analyse.
- Das Verhalten von Bauelementen mit nicht-linearerKennliniewird bei kleinen Signaländerungen in der Umgebung eines Bezugspunktes durch ihrKleinsignalverhaltenbeschrieben; dieses basiert auf dem Verlauf der Tangente an die Kennlinie im Bezugspunkt.
- Die Ableitung nach der Zeit ist im untersuchten Sachverhalt diemomentane Änderungsrate.So ist beispielsweise die Ableitung der Orts- beziehungsweise Weg-Zeit-Funktion eines Teilchens nach der Zeit seine Momentangeschwindigkeit, und die Ableitung der Momentangeschwindigkeit nach der Zeit liefert die momentane Beschleunigung.
- In den Wirtschaftswissenschaften spricht man auch häufig von Grenzraten anstelle der Ableitung, zum BeispielGrenzkostenoder Grenzproduktivität eines Produktionsfaktors.
In der Sprache derGeometrieist die Ableitung eine verallgemeinerte Steigung. Der geometrische Begriff Steigung ist ursprünglich nur fürlineare Funktionendefiniert, derenFunktionsgrapheine Gerade ist. Die Ableitung einer beliebigen Funktion an einer Stellekann man als die Steigung derTangenteim PunktdesGraphenvondefinieren.
In der Sprache derArithmetikschreibt manfür die Ableitung einer Funktionan der Stelle.Sie gibt an, um welchen Faktor vonsichungefähr ändert, wenn sichum einen „kleinen “Betragändert. Für die exakte Formulierung dieses Sachverhalts wird der BegriffGrenzwertoderLimesverwendet.
Einführung
[Bearbeiten|Quelltext bearbeiten]Heranführung anhand eines Beispiels
[Bearbeiten|Quelltext bearbeiten]Fährt ein Auto auf einer Straße, so kann anhand dieses Sachverhalts eine Tabelle erstellt werden, in der zu jedem Zeitpunkt die Strecke, die seit dem Beginn der Aufzeichnung zurückgelegt wurde, eingetragen wird. In der Praxis ist es zweckmäßig, eine solche Tabelle nicht zu engmaschig zu führen, d. h. zum Beispiel in einem Zeitraum von 1 Minute nur alle 3 Sekunden einen neuen Eintrag zu machen, was lediglich 20 Messungen erfordern würde. Jedoch kann eine solche Tabelle theoretisch beliebig engmaschig gestaltet werden, wenn jeder Zeitpunkt berücksichtigt werden soll. Dabei gehen die vormals diskreten, also mit einem Abstand behafteten Daten, in ein Kontinuum über. DieGegenwartwird dann als Zeitpunkt,d. h. als ein unendlich kurzer Zeitabschnitt, interpretiert. Gleichzeitig hat das Auto aber zu jedem Zeitpunkt eine theoretisch bekannte Strecke zurückgelegt, und wenn es nicht bis zum Stillstand abbremst oder gar zurück fährt, wird die Strecke kontinuierlich ansteigen, also zu keinem Zeitpunkt dieselbe sein wie zu einem anderen.
-
Exemplarische Darstellung einer Tabelle, alle 3 Sekunden wird eine neue Messung eingetragen. Unter solchen Voraussetzungen können lediglich durchschnittliche Geschwindigkeiten in den Zeiträumen 0 bis 3, 3 bis 6 usw. Sekunden berechnet werden. Da die zurückgelegte Strecke stets zunimmt, scheint der Wagen nur vorwärts zu fahren. -
Übergang zu einer beliebig engmaschigen Tabelle, die nach Eintragung aller Punkte die Gestalt einer Kurve annimmt.JedemZeitpunkt zwischen 0 und 60 Sekunden wird ein Punkt auf der Kurve zugeordnet. Regionen, innerhalb derer die Kurve steiler nach oben verläuft, entsprechen Zeitabschnitten, in denen eine größere Strecke pro Zeitspanne zurückgelegt wird. In Regionen mit nahezu gleich bleibender Strecke, zum Beispiel im Bereich 15–20 Sekunden, fährt das Auto langsam und die Kurve verläuft flach.
Die Motivation hinter dem Begriff derAbleitungeiner Weg-Zeit-Kurve oder -Funktion ist, dass nun angegeben werden kann,wie schnellsich das Auto zu einem momentanen Zeitpunkt bewegt. Aus einem Weg-Zeit-Verlauf soll also der passende Geschwindigkeit-Zeit-Verlaufabgeleitetwerden. Hintergrund ist, dass die Geschwindigkeit ein Maß dafür ist,wie starksich die zurückgelegte Strecke im Laufe der Zeitändert.Bei einer hohen Geschwindigkeit ist ein starker Anstieg in der Kurve zu sehen, während eine niedrige Geschwindigkeit zu wenig Veränderung führt. DajedemMesspunkt auch eine Strecke zugeordnet wurde, sollte eine solche Analyse grundsätzlich möglich sein, denn mit dem Wissen über die zurückgelegte Streckeinnerhalb einem Zeitintervallgilt für die Geschwindigkeit
Sind alsoundzwei unterschiedliche Zeitpunkte, so lautet „die Geschwindigkeit “des Autos im Zeitintervall zwischen diesen
Die Differenzen in Zähler und Nenner müssen gebildet werden, da man sich nur für die innerhalb eines bestimmten Zeitintervallszurückgelegte Streckeinteressiert. Dennoch liefert dieser Ansatz kein vollständiges Bild, da zunächst nur Geschwindigkeiten für Zeitintervalle mit auseinander liegendem Anfangs- und Endpunkt gemessen wurden. EinemomentaneGeschwindigkeit, vergleichbar mit einemBlitzerfoto,hingegen bezöge sich auf einunendlich kurzes Zeitintervall.Dementsprechend ist der oben stehende Begriff „Geschwindigkeit “durch „durchschnittliche Geschwindigkeit “zu präzisieren. Auch wenn mit echten Zeitintervallen, also diskreten Daten, gearbeitet wird, vereinfacht sich das Modell insofern, als für ein Auto innerhalb der betrachteten Intervalle keine schlagartige Ortsänderung und keine schlagartige Geschwindigkeitsänderung möglich ist. (Auch eine Vollbremsung benötigt Zeit, und zwar länger als die Zeit, in der die Reifen quietschen.) Damit ist auch in der Zeichnung der stillschweigenddurchgehendeingetragene Kurvenzug ohne Sprung und ohne Knick gerechtfertigt.

Soll hingegen zu einem „perfekt passenden “Geschwindigkeit-Zeit-Verlauf übergegangen werden, so muss der Terminus „durchschnittliche Geschwindigkeit in einem Zeitintervall “durch „Geschwindigkeit zu einem Zeitpunkt “ersetzt werden. Dazu muss zunächst ein Zeitpunktgewählt werden. Die Idee ist nun, „ausgedehnte Zeitintervalle “in einemGrenzwertprozessgegen ein unendlich kurzes Zeitintervall laufen zu lassen und zu studieren, was mit den betroffenen durchschnittlichen Geschwindigkeiten passiert. Obwohl der Nennerdabei gegen 0 strebt, ist dies anschaulich kein Problem, da sich das Auto in kürzer werdenden Zeitabschnitten beistetigemVerlauf immer weniger weit bewegen kann, womit sich Zähler und Nenner gleichzeitig verkleinern, und im Grenzprozess ein unbestimmter Term „“entsteht. Dieser kann unter Umständen als Grenzwert Sinn ergeben, beispielsweise drücken
exaktdieselbenGeschwindigkeiten aus. Nun gibt es zwei Möglichkeiten beim Studium der Geschwindigkeiten. Entweder, sie lassen in dem betrachteten GrenzwertprozesskeineTendenz erkennen, sich einem bestimmten endlichen Wert anzunähern. In diesem Fall kann der Bewegung des Autoskeine zum Zeitpunktgültige Geschwindigkeitzugeordnet werden, d. h., der Term „“hat hier keinen eindeutigen Sinn. Gibt es hingegen eine zunehmende Stabilisierung in Richtung auf einen festen Wert, soexistiertderGrenzwert
und drückt die exakt im Zeitpunktbestehende Geschwindigkeit aus. Der unbestimmte Term „“nimmt in diesem Fall einen eindeutigen Wert an. Die dabei entstehende Momentangeschwindigkeit wird auch als Ableitung vonan der Stellebezeichnet; für diese wird häufig das Symbolbenutzt. Mit dem Grenzwert wird die Momentangeschwindigkeit zu einem beliebigen Zeitpunkt definiert als
Prinzip der Differentialrechnung
[Bearbeiten|Quelltext bearbeiten]
Das Beispiel des letzten Abschnitts ist dann besonders einfach, wenn die Zunahme der zurückgelegten Strecke mit der Zeitgleichförmig,also linear verläuft. Dann liegt speziell eineProportionalitätzwischen derVeränderungder Strecke und derVeränderungder Zeit vor. Dierelative Veränderungder Strecke, also ihre Zunahme im Verhältnis zur Zunahme der Zeit, ist bei dieser Bewegung immer gleichbleibend. DiemittlereGeschwindigkeit ist zu jedem Zeitpunkt auch diemomentaneGeschwindigkeit. Beispielsweise legt das Auto zwischen 0 und 1 Sekunden eine gleich lange Strecke zurück wie zwischen 9 und 10 Sekunden und die zehnfache Strecke zwischen 0 und 10 Sekunden. Als Proportionalitätsfaktor über den ganzen Weg gilt die konstante Geschwindigkeit,wobei sie im nebenstehenden Bildbeträgt. Die zwischen beliebig weit auseinanderliegenden Zeitpunktenundzurückgelegte Strecke beträgt
- .
Allgemein bewegt sich das Auto in der Zeitspanneum die Streckevorwärts. Speziell beiergibt sich ein Wegstück.
Falls der Startwert beinichtsondernbeträgt, ändert dies nichts, da sich in der Beziehungdie Konstantedurch dieDifferenzbildungausstets heraussubtrahiert. Auch anschaulich ist dies bekannt: Die Startposition des Autos ist unerheblich für seine Geschwindigkeit.
Werden statt derVariablenundallgemein die Variablenundbetrachtet, so lässt sich also festhalten:
- Lineare Funktionen:BeiLinearitäthat die betrachtete Funktion die Gestalt.(Für eine lineare Funktion ist nicht notwendig eineUrsprungsgeradeerforderlich!) Als Ableitung gilt hieran dierelative Veränderung,mit einem anderen Wort derDifferenzenquotient.Sie hat in jedem Punkt denselben Wert.Die Ableitung lässt sich aus dem Ausdruckdirekt ablesen. Insbesondere hat jedekonstante Funktiondie Ableitung,da sich mit einer Änderung des Eingabewertes nichts am Ausgabewert ändert.
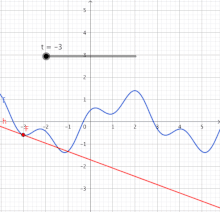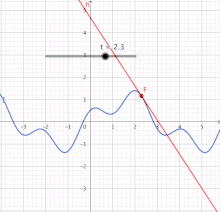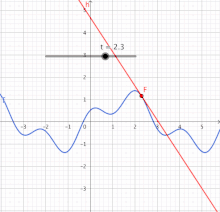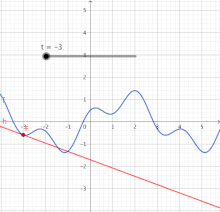
Schwieriger wird es, wenn eine Bewegungnicht gleichförmigverläuft. Dann ist das Diagramm der Zeit-Strecken-Funktion nicht geradlinig. Für derartige Verläufe muss der Ableitungsbegriff erweitert werden. Denn es gibt keinen Proportionalitätsfaktor, derüberalldie lokale relative Veränderung ausdrückt. Als einzig mögliche Strategie ist die Gewinnung einerlinearen Näherungfür die nicht-lineare Funktion gefunden worden, zumindest an einer interessierenden Stelle. (Im nächsten Bild ist das die Stelle.) Damit wird das Problem auf eine wenigstens an dieser Stelle lineare Funktion zurückgeführt. Die Methode derLinearisierungist die Grundlage für den eigentlichenKalkülder Differentialrechnung. Sie ist in derAnalysisvon sehr großer Bedeutung, da sie dabei hilft, komplizierte Vorgänge lokal auf leichter verständliche Vorgänge, nämlich lineare Vorgänge, zu reduzieren.[1]
| 0,5 | 0,9 | 0,99 | 0,999 | 1 | 1,001 | 1,01 | 1,1 | 1,5 | 2 | |
| 0,25 | 0,81 | 0,9801 | 0,998001 | 1 | 1,002001 | 1,0201 | 1,21 | 2,25 | 4 | |
| 0 | 0,8 | 0,98 | 0,998 | 1 | 1,002 | 1,02 | 1,2 | 2 | 3 | |
| −0,25 | −0,01 | −0,0001 | −0,000001 | 0 | −0,000001 | −0,0001 | −0,01 | −0,25 | −1 | |
| 50 % | 10 % | 1 % | 0,1 % | 0,1 % | 1 % | 10 % | 50 % | 100 % |
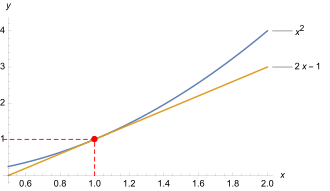
Die Strategie soll exemplarisch an der nicht-linearen Funktionerläutert werden.[2]Die Tabelle zeigt Werte für diese Funktion und für ihre Näherungsfunktion an der Stelle,das ist.Darunter enthält die Tabelle die Abweichung der Näherung von der ursprünglichen Funktion. (Die Werte sind negativ, weil in diesem Fall die Gerade immerunterder Kurve liegt – außer im Berührpunkt.) In der letzten Zeile steht der Betrag derrelativen Abweichung,das ist die Abweichung bezogen auf die Entfernung der Stellevom Berührpunkt bei.Diese kann am Berührpunkt nicht berechnet werden. Aber die Werte in der Umgebung zeigen, wie sich die relative Abweichung einem Grenzwert nähert, hier dem Wert null. Diese Null bedeutet: Selbst wenn sichein wenig (infinitesimal) vom Berührpunkt entfernt, entsteht noch kein Unterschied zwischenund.
Die lineare Funktionahmt das Verhalten vonnahe der Stellegut nach (besser als jede andere lineare Funktion). Die relative Veränderunghat überall den Wert.Die nicht so einfach zu ermittelnde relative Veränderungstimmt aber im Berührpunkt mit dem Wertüberein.
Es lässt sich also festhalten:
- Nicht-lineare Funktionen:Soll die relative Veränderung einer nicht-linearen Funktion in einem bestimmten Punkt ermittelt werden, so wird sie (wenn möglich) dort linear genähert. Die Steigung der linearen Näherungsfunktion ist die an dieser Stelle vorliegende Steigung der betrachteten nicht-linearen Funktion, und es gilt dieselbe Anschauung wie bei Ableitungen linearer Funktionen. Dabei ist nur zu beachten, dass sich die relative Veränderung einer nicht-linearen Funktion von Punkt zu Punkt ändert.
- Während im Beispiel oben (Fahrzeugbewegung) für die durchschnittliche Geschwindigkeit die Zeitspanneangemessen willkürlich gewählt werden kann, ist die momentane Geschwindigkeit, wenn sie veränderlich ist, nur fürkleineangebbar. Wie kleingewählt werden muss, hängt ab von der Anforderung an die Qualität der Näherung. In mathematischer Perfektion wird sie infinitesimal. Bei dieser wird für die relative Veränderung (wie schon oben angegeben) anstelle des DifferenzenquotientenderDifferenzialquotientgeschrieben (in vereinfachter Schreibweiseoder).
Die Gewinnung der linearen Näherung einer nicht-linearen Funktion an einer bestimmten Stelle ist zentrale Aufgabe des Kalküls der Differentialrechnung. Bei einer mathematisch angebbaren Funktion (im Beispiel war das) sollte sich die Ableitungausrechnenlassen. Im Idealfall ist diese Berechnung sogar so allgemein, dass sie auf alle Punkte des Definitionsbereichs angewendet werden kann. Im Falle vonbesitzt jede Stelleals beste lineare Näherung die Steigung.Mit der Zusatzinformation, dass die lineare Funktion mit der Kurve im Punktübereinstimmen muss, kann dann die vollständige Funktionsgleichung der linearen Näherungsfunktion aufgestellt werden.
Der Ansatz zur Bestimmung des Differentialquotienten liegt in der Berechnung des Grenzwerts (wie oben bei der momentanen Geschwindigkeit):
- oder in anderer Schreibweise
Bei einigen elementaren Funktionen wiePotenzfunktion,Exponentialfunktion,LogarithmusfunktionoderSinusfunktionist jeweils der Grenzwertprozess durchgeführt worden. Dabei ergibt sich jeweils eineAbleitungsfunktion.Darauf aufbauend sindAbleitungsregelnfür die elementaren und auch für weitere Funktionen wieSummen,ProdukteoderVerkettungen elementarer Funktionenaufgestellt worden.
Damit werden die Grenzübergänge nicht in jeder Anwendung neu vollzogen, sondern für die Rechenpraxis werden Ableitungsregeln angewendet. Die „Kunst “der Differentialrechnung besteht „nur “darin, kompliziertere Funktionen zu strukturieren und auf die Strukturelemente die jeweils zutreffende Ableitungsregel anzuwenden. Ein Beispiel folgtweiter hinten.
Berechnung von Grenzwerten
[Bearbeiten|Quelltext bearbeiten]Jeder Differenzialquotient an einer vorgesehenen Stelle erscheint als unbestimmter Ausdruck vom Typ „“.Zu seiner Berechnung wird vomDifferenzenquotientausgegangen, und dessen Verhalten in der Umgebung der vorgesehenen Stelle wird untersucht, ob er die Tendenz hat, einen bestimmten Wert anzunehmen. Einige Grenzwerte, die für Ableitungsregeln benötigt werden, werden nachfolgend hergeleitet. Selbstverständlich dürfen dazu keine Regeln der Differenzialrechnung verwendet werden, da diese erst nach der Kenntnis der Grenzwerte aufgestellt werden können.
- Ein einfacher Fall 1
Ausgangspunkt ist der Differenzenquotient für die vorgesehene Funktion.
Wird diebinomische Formeleingesetzt, so kürzt sich ein Summand heraus.
Fürist dieser Bruch unbestimmt. Aber für(dann und nur dann!) können Zähler und Nenner durchdividiert werden.
Für jedesist dieser Ausdruck bestimmt, auch wenn man dem Wertnahe kommt. Er strebt im Grenzübergang nach
Im Weiteren werden hier nur Grenzwerte berechnet, und ihre Einsetzung in Differenzenquotienten erfolgt weiter hinten im AbschnittAbleitungsberechnung.

- Fall 2
Fürist dieser Bruch unbestimmt. Zur Berechnung beiwird die Fläche einesKreissektorsmit dem Bogenverglichen mit den Flächen eines innen liegenden und eines außen liegenden Dreiecks gemäß der Zeichnung. Im gezeigten Quadranten gilt offensichtlich[3]
Beikann diese Ungleichung mitmultipliziert werden.
Fürstreben sowohl der linke als auch der rechte Ausdruck gegen eins. Damit muss auch der dazwischen liegende Ausdruck gegen eins streben. Für seinen Kehrwert gilt das ebenfalls. Fürstrebt er im Grenzübergang nach
- Zwischenüberlegung
Der Logarithmus dieses Ausdrucks, das ist,strebt fürgegen „“.Dieser Logarithmus ist dort unbestimmt und damit auch der Ausdruck selber. Es ist aber bewiesen, dass
einen bestimmten endlichen Wert annimmt, der alsEulersche Zahlbezeichnet wird. Dieses wird unter dem verlinkten Stichwort behandelt und hier als bekannt vorausgesetzt.
- Fall 3
Fürist dieser Bruch unbestimmt. Aber fürundist dieSubstitution[4]
- ,
zulässig. Aufgelöst nachunter Verwendung desnatürlichen Logarithmusergibt das
Fürstrebenund der Nenner gegen.Für jedesist dieser Ausdruck bestimmt, auch wenn man dem Wertnahe kommt. Er strebt im Grenzübergang nach
Als Voraussetzung für diese Herleitung musspositiv sein. Fürist dieses erfüllt mit negativem.Nähert man sich beidem Wertvon der Seiteher, so gilt derselbe Grenzübergang.
- Fall 4
Fürist dieser Bruch unbestimmt. Aber fürist die Substitutionzulässig.[5]
Fürstrebt.Für jedesist dieser Ausdruck bestimmt, auch wenn man dem Wertnahe kommt. Er strebt im Grenzübergang nach
Einordnung der Anwendungsmöglichkeiten
[Bearbeiten|Quelltext bearbeiten]Extremwertprobleme
[Bearbeiten|Quelltext bearbeiten]Eine wichtige Anwendung der Differentialrechnung besteht darin, dass mit Hilfe der Ableitung lokale Extremwerte einer Kurve bestimmt werden können. Anstatt also anhand einer Wertetabelle mechanisch nach Hoch- oder Tiefpunkten suchen zu müssen, liefert der Kalkül in einigen Fällen eine direkte Antwort. Liegt ein Hoch- oder Tiefpunkt vor, so besitzt die Kurve an dieser Stelle keinen „echten “Anstieg, weshalb die optimale Linearisierung eine Steigung von 0 besitzt. Für die genaue Klassifizierung eines Extremwertes sind jedoch weitere lokale Daten der Kurve notwendig, denn eine Steigung von 0 ist nicht hinreichend für die Existenz eines Extremwertes (geschweige denn eines Hoch- oder Tiefpunktes).
In der Praxis treten Extremwertprobleme typischerweise dann auf, wenn Prozesse, zum Beispiel in der Wirtschaft, optimiert werden sollen. Oft liegen an den Randwerten jeweils ungünstige Ergebnisse, in Richtung „Mitte “kommt es aber zu einer stetigen Steigerung, die dann irgendwo maximal werden muss. Zum Beispiel die optimale Wahl eines Verkaufspreises: Bei einem zu geringen Preis ist die Nachfrage nach einem Produkt zwar sehr groß, aber die Produktion kann nicht finanziert werden. Ist er andererseits zu hoch, so wird es im Extremfall gar nicht mehr gekauft. Daher liegt ein Optimum irgendwo „in der Mitte “. Voraussetzung dabei ist, dass der Zusammenhang in Form einer (stetig) differenzierbaren Funktion wiedergegeben werden kann.
Die Untersuchung einer Funktion auf Extremstellen ist Teil einerKurvendiskussion.Die mathematischen Hintergründe sind im AbschnittAnwendung höherer Ableitungenbereitgestellt.
Mathematische Modellierung
[Bearbeiten|Quelltext bearbeiten]In dermathematischen Modellierungsollen komplexe Probleme in mathematischer Sprache erfasst und analysiert werden. Je nach Fragestellung sind das Untersuchen vonKorrelationenoderKausalitätenoder auch das Geben vonPrognosenim Rahmen dieses Modells zielführend.
Besonders im Umfeld sog.Differentialgleichungenist die Differentialrechnung zentrales Werkzeug bei der Modellierung. Diese Gleichungen treten zum Beispiel auf, wenn es eine kausale Beziehung zwischen demBestandeiner Größe und derenzeitlicher Veränderunggibt. Ein alltägliches Beispiel könnte sein:
- Je mehr Einwohner eine Stadt besitzt, desto mehr Leute wollen dort hinziehen.
Etwas konkreterkönntedies zum Beispiel heißen, dass beijetzigen Einwohnern durchschnittlichPersonen in den kommenden 10 Jahren zuziehen werden, beiEinwohnern durchschnittlichPersonen in den kommenden 10 Jahren usw. – um nicht alle Zahlen einzeln ausführen zu müssen: LebenPersonen in der Stadt, so wollen so viele Menschen hinzuziehen, dass nach 10 Jahren weiterehinzukommen würden. Besteht eine derartige Kausalität zwischen Bestand und zeitlicher Veränderung, so kann gefragt werden, ob aus diesen Daten eine Prognose für die Einwohnerzahl nach 10 Jahren abgeleitet werden kann, wenn die Stadt im Jahr 2020 zum BeispielEinwohner hatte. Es wäre dabei falsch zu glauben, dass diessein werden, da sich mit steigender Einwohnerzahl auch die Nachfrage nach Wohnraum wiederum zunehmend steigern wird. Der Knackpunkt zum Verständnis des Zusammenhangs ist demnach erneut dessenLokalität:Besitzt die StadtEinwohner, so wollenzu diesem ZeitpunktMenschen pro 10 Jahre hinzuziehen. Aber einen kurzen Augenblick später, wenn weitere Menschen hinzugezogensind,sieht die Lage wieder anders aus. Wird dieses Phänomen zeitlich beliebig engmaschig gedacht, ergibt sich ein „differentieller “Zusammenhang. Allerdings eignet sich die kontinuierliche Herangehensweise in vielen Fällen auch bei diskreten Problemstellungen.[6]
Mit Hilfe der Differentialrechnung kann aus so einem kausalen Zusammenhang zwischen Bestand und Veränderung in vielen Fällen ein Modell hergeleitet werden, was den komplexen Zusammenhangauflöst,und zwar in dem Sinne, dass zum Schluss eine Bestandsfunktionexplizit angegeben werden kann.Setzt man in diese Funktion dann zum Beispiel den Wert 10 Jahre ein, so ergibt sich eine Prognose für die Stadtbewohneranzahl im Jahr 2030. Im Falle oberen Modells wird eine Bestandsfunktiongesucht mit,in 10 Jahren, und.Die Lösung ist dann
mit dernatürlichen Exponentialfunktion(natürlichbedeutet, dass der Proportionalitätsfaktor zwischen Bestand und Veränderung einfach gleich 1 ist) und für das Jahr 2030 lautet die geschätzte PrognoseMio. Einwohner. Die Proportionalität zwischen Bestand und Veränderungsrate führt also zuexponentiellem Wachstumund ist klassisches Beispiel einesselbstverstärkenden Effektes.Analoge Modelle funktionieren beimPopulationswachstum(Je mehr Individuen, desto mehr Geburten) oder der Verbreitung einer ansteckenden Krankheit (Je mehr Erkrankte, desto mehr Ansteckungen). In vielen Fällen stoßen diese Modelle jedoch an eine Grenze, wenn sich der Prozess aufgrund natürlicher Beschränkungen (wie eine Obergrenze der Gesamtbevölkerung) nicht beliebig fortsetzen lässt. In diesen Fällen sind ähnliche Modelle, wie daslogistische Wachstum,geeigneter.[7]
Numerische Verfahren
[Bearbeiten|Quelltext bearbeiten]Die Eigenschaft einer Funktion, differenzierbar zu sein, ist bei vielen Anwendungen von Vorteil, da dies der Funktion mehr Struktur verleiht. Ein Beispiel ist das Lösen von Gleichungen. Bei einigen mathematischen Anwendungen ist es notwendig, den Wert einer (oder mehrerer) Unbekanntenzu finden, die Nullstelle einer Funktionist. Es ist dann.Je nach Beschaffenheit vonkönnen Strategien entwickelt werden, eine Nullstelle zumindest näherungsweise anzugeben, was in der Praxis meist vollkommen ausreicht. Istin jedem Punkt differenzierbar mit Ableitung,so kann in vielen Fällen dasNewton-Verfahrenhelfen. Bei diesem spielt die Differentialrechnung insofern eine direkte Rolle, als beim schrittweisen Vorgehen immer wieder eine Ableitung explizit berechnet werden muss.[8]
Ein weiterer Vorteil der Differentialrechnung ist, dass in vielen Fällen komplizierte Funktionen, wie Wurzeln oder auch Sinus und Kosinus, anhand einfacher Rechenregeln wie Addition und Multiplikation gut angenähert werden können. Ist die Funktion an einem benachbarten Wert leicht auszuwerten, ist dies von großem Nutzen. Wird zum Beispiel nach einem Näherungswert für die Zahlgesucht, so liefert die Differentialrechnung fürdie Linearisierung
denn es gilt nachweislich.Sowohl Funktion als auch erste Ableitung konnten an der Stellegut berechnet werden, weil es sich dabei um eineQuadratzahlhandelt. Einsetzen vonergibt,was mit dem exakten Ergebnisbis auf einen Fehler kleiner alsübereinstimmt.[9]Unter EinbezughöhererAbleitungen kann die Genauigkeit solcher Approximationen zusätzlich gesteigert werden, da dann nicht nur linear, sondernquadratisch, kubischusw. angenähert wird, siehe auchTaylor-Reihe.
Reine Mathematik
[Bearbeiten|Quelltext bearbeiten]
Auch in derreinen Mathematikspielt die Differentialrechnung als ein Kern der Analysis eine bedeutende Rolle. Ein Beispiel ist dieDifferentialgeometrie,die sich mit Figuren beschäftigt, die eine differenzierbare Oberfläche (ohne Knicke usw.) haben. Zum Beispiel kann auf eineKugeloberflächein jedem Punkt tangential eineEbeneplatziert werden. Anschaulich: Steht man an einem Erdpunkt, so hat man das Gefühl, die Erde sei flach, wenn man seinen Blick in derTangentialebeneschweifen lässt. In Wahrheit ist die Erde jedoch nurlokal flach:Die angelegte Ebene dient der (durchLinearisierung) vereinfachten Darstellung der komplizierteren Krümmung.Globalhat sie als Kugeloberfläche eine völlig andere Gestalt.
Die Methoden der Differentialgeometrie sind äußerst bedeutend für dietheoretische Physik.So können Phänomene wieKrümmungoderRaumzeitüber Methoden der Differentialrechnung beschrieben werden. Auch die Frage, was der kürzeste Abstand zwischen zwei Punkten auf einer gekrümmten Fläche (zum Beispiel der Erdoberfläche) ist, kann mit diesen Techniken formuliert und oft auch beantwortet werden.
Auch bei der Erforschung von Zahlen als solchen, also im Rahmen derZahlentheorie,hat sich die Differentialrechnung in deranalytischen Zahlentheoriebewährt. Die grundlegende Idee der analytischen Zahlentheorie ist die Umwandlung von bestimmten Zahlen, über die man etwas lernen möchte,in Funktionen.Haben diese Funktionen „gute Eigenschaften “wie etwa Differenzierbarkeit, so hofft man, über die damit einhergehenden Strukturen Rückschlüsse auf die ursprünglichen Zahlen ziehen zu können. Es hat sich dabei häufig bewährt, zur Perfektionierung der Analysis von den reellen zu den komplexen Zahlen überzugehen (siehe auchkomplexe Analysis), also die Funktionen über einem größeren Zahlenbereich zu studieren. Ein Beispiel ist die Analyse derFibonacci-Zahlen,deren Bildungsgesetz vorschreibt, dass eine neue Zahl stets aus der Summe der beiden vorangehenden entstehen soll. Ansatz der analytischen Zahlentheorie ist die Bildung dererzeugenden Funktion
also eines „unendlich langen “Polynoms(einer sog.Potenzreihe), dessenKoeffizientengenau die Fibonacci-Zahlen sind. Für hinreichend kleine Zahlenist dieser Ausdruck sinnvoll, weil die Potenzendann viel schneller gegen 0 gehen als die Fibonacci-Zahlen gegen Unendlich, womit sich langfristig alles bei einem endlichen Wert einpendelt. Es ist für diese Werte möglich, die Funktionexplizit zu berechnen durch
Das Nennerpolynom„spiegelt “dabei genau das Verhaltender Fibonacci-Zahlen„wider “– es ergibt sich in der Tatdurch termweises Verrechnen. Mit Hilfe der Differentialrechnung lässt sich andererseits zeigen, dass die Funktionausreicht, um die Fibonacci-Zahlen (ihre Koeffizienten) eindeutig zu charakterisieren. Da es sich aber um eine schlichterationale Funktionhandelt, lässt sich dadurch die für jede Fibonacci-Zahlgültigeexakte Formel
mit demgoldenen Schnittherleiten, wennundgesetzt wird. Die exakte Formel vermag eine Fibonacci-Zahl zu berechnen, ohne die vorherigen zu kennen. Der Schluss wird über einen sog.Koeffizientenvergleichgezogen und nutzt aus, dass das Polynomals Nullstellenundbesitzt.[10]
Der höherdimensionale Fall
[Bearbeiten|Quelltext bearbeiten]Die Differentialrechnung kann auf den Fall „höherdimensionaler Funktionen “verallgemeinert werden. Damit ist gemeint, dass sowohl Eingabe- als auch Ausgabewerte der Funktion nicht bloß Teil des eindimensionalen reellenZahlenstrahls,sondern auch Punkte eines höherdimensionalen Raums sind. Ein Beispiel ist die Vorschrift
zwischen jeweils zweidimensionalen Räumen. Das Funktionsverständnis als Tabelle bleibt hier identisch, nur dass diese mit „vier Spalten “„deutlich mehr “Einträge besitzt. Auch mehrdimensionale Abbildungen können in manchen Fällen an einem Punkt linearisiert werden. Allerdings ist dabei nun angemessen zu beachten, dass es sowohl mehrere Eingabedimensionen als auch mehrere Ausgabedimensionen geben kann: Der korrekte Verallgemeinerungsweg liegt darin, dass die Linearisierung injeder Komponenteder Ausgabejede Variableauflineare Weiseberücksichtigt. Das zieht für obere Beispielfunktion eine Approximation der Form
nach sich. Diese ahmt dann die gesamte Funktion in der Nähe der Eingabesehr gut nach.[11]InjederKomponente wird demnach für jede Variable eine „Steigung “angegeben – diese wird dann das lokale Verhalten der Komponentenfunktion bei kleiner Änderung in dieser Variablen messen. Diese Steigung wird auch alspartielle Ableitungbezeichnet.[12]Die korrekten konstanten Abschnitteberechnen sich exemplarisch durchbzw..Wie auch im eindimensionalen Fall hängen die Steigungen (hier) stark von der Wahl des Punktes (hier) ab, an dem abgeleitet wird. Die Ableitung ist demnach keine Zahl mehr, sondern ein Verband aus mehreren Zahlen – in diesem Beispiel sind es vier – und diese Zahlen sind im Regelfall bei allen Eingaben unterschiedlich. Es wird allgemein für die Ableitung auch
geschrieben, womit alle „Steigungen “in einer sog.Matrixversammelt sind. Man bezeichnet diesen Term auch alsJacobi-MatrixoderFunktionalmatrix.[13]
Beispiel:Wird obengesetzt, so kann man zeigen, dass folgende lineare Approximation bei sehr kleinen Änderungen vonundsehr gut ist:
Zum Beispiel gilt
und
Hat man im ganz allgemeinen FallVariablen undAusgabekomponenten, so gibt es kombinatorisch gesehen insgesamt„Steigungen “, also partielle Ableitungen. Im klassischen Fallgibt es wegeneine Steigungund im oberen Beispielsind es„Steigungen “.[14]
Geschichte
[Bearbeiten|Quelltext bearbeiten]

Die Aufgabenstellung der Differentialrechnung bildete sich alsTangentenproblemab dem 17. Jahrhundert heraus. Hierunter versteht man die Aufgabe, bei einer beliebigen Kurve in einem beliebigen Punkt die Tangente zu bestimmen.[15]Ein naheliegender Lösungsansatz bestand darin, die Tangente an eine Kurve durch ihreSekanteüber einem endlichen (endlichheißt hier: größer als null), aber beliebig kleinenIntervallzu approximieren. Dabei war die technische Schwierigkeit zu überwinden, mit einer solcheninfinitesimalkleinen Intervallbreite zu rechnen. Die ersten Anfänge der Differentialrechnung gehen aufPierre de Fermatzurück. Er entwickelte um 1628 eine Methode, Extremstellen algebraischer Terme zu bestimmen und Tangenten an Kegelschnitte und andere Kurven zu berechnen. Seine „Methode “war rein algebraisch. Fermat betrachtete keine Grenzübergänge und schon gar keine Ableitungen. Gleichwohl lässt sich seine „Methode “mit modernen Mitteln der Analysis interpretieren und rechtfertigen, und sie hat Mathematiker wie Newton und Leibniz nachweislich inspiriert. Einige Jahre später wählteRené Descarteseinen anderen algebraischen Zugang, indem er an eine Kurve einen Kreis anlegte. Dieser schneidet die Kurve in zwei nahe beieinanderliegenden Punkten; es sei denn, er berührt die Kurve. Dieser Ansatz ermöglichte es ihm, für spezielle Kurven die Steigung der Tangente zu bestimmen.[16]
Ende des 17. Jahrhunderts gelang esIsaac NewtonundGottfried Wilhelm Leibnizmit unterschiedlichen Ansätzen unabhängig voneinander, widerspruchsfrei funktionierende Kalküle zu entwickeln. Während Newton das Problem physikalisch über das Momentangeschwindigkeitsproblem anging,[17]löste es Leibniz geometrisch über das Tangentenproblem. Ihre Arbeiten erlaubten das Abstrahieren von rein geometrischer Vorstellung und werden deshalb als Beginn der Analysis betrachtet. Bekannt wurden sie vor allem durch das BuchAnalyse des Infiniment Petits pour l’Intelligence des Lignes Courbes[18]des AdligenGuillaume François Antoine, Marquis de L’Hospital,der beiJohann I BernoulliPrivatunterricht nahm und dessen Forschung zur Analysis so publizierte. Darin heißt es:
„Die Reichweite dieses Kalküls ist unermesslich: Er lässt sich sowohl auf mechanische als auch geometrische Kurven anwenden; Wurzelzeichen bereiten ihm keine Schwierigkeiten und sind oftmals sogar angenehm im Umgang; er lässt sich auf so viele Variablen erweitern, wie man sich nur wünschen kann; der Vergleich unendlich kleiner Größen aller Art gelingt mühelos. Und er erlaubt eine unendliche Zahl an überraschenden Entdeckungen über gekrümmte wie geradlinige Tangenten, FragenDe maximis & minimis,Wendepunkte und Spitzen von Kurven, Evoluten, Spiegelungs- und Brechungskaustiken, &c. wie wir in diesem Buch sehen werden. “[19]
Die heute bekannten Ableitungsregeln basieren vor allem auf den Werken vonLeonhard Euler,der den Funktionsbegriff prägte.
Newton und Leibniz arbeiteten mit beliebig kleinen positiven Zahlen.[20]Dies wurde bereits von Zeitgenossen als unlogisch kritisiert, beispielsweise vonGeorge Berkeleyin der polemischen SchriftThe analyst; or, a discourse addressed to an infidel mathematician.[21]Erst in den 1960ern konnteAbraham Robinsondiese Verwendung infinitesimaler Größen mit der Entwicklung derNichtstandardanalysisauf ein mathematisch-axiomatisch sicheres Fundament stellen. Trotz der herrschenden Unsicherheit wurde die Differentialrechnung aber konsequent weiterentwickelt, in erster Linie wegen ihrer zahlreichen Anwendungen in der Physik und in anderen Gebieten der Mathematik. Symptomatisch für die damalige Zeit war das von derPreußischen Akademie der Wissenschaften1784 veröffentlichte Preisausschreiben:
„… Die höhere Geometrie benutzt häufig unendlich große und unendlich kleine Größen; jedoch haben die alten Gelehrten das Unendliche sorgfältig vermieden, und einige berühmte Analysten unserer Zeit bekennen, dass die Wörter unendliche Größe widerspruchsvoll sind. Die Akademie verlangt also, dass man erkläre, wie aus einer widersprechenden Annahme so viele richtige Sätze entstanden sind, und dass man einen sicheren und klaren Grundbegriff angebe, welcher das Unendliche ersetzen dürfte, ohne die Rechnung zu schwierig oder zu lang zu machen… “[22]
Erst zum Anfang des 19. Jahrhunderts gelang esAugustin-Louis Cauchy,der Differentialrechnung die heute übliche logische Strenge zu geben, indem er von den infinitesimalen Größen abging und die Ableitung alsGrenzwertvonSekantensteigungen(Differenzenquotienten) definierte.[23]Die heute benutzte Definition des Grenzwerts wurde schließlich vonKarl Weierstraßim Jahr 1861 formuliert.[24]
Definition
[Bearbeiten|Quelltext bearbeiten]Sekanten- und Tangentensteigung
[Bearbeiten|Quelltext bearbeiten]Ausgangspunkt für die Definition der Ableitung ist die Näherung der Tangentensteigung durch eine Sekantensteigung (manchmal auch Sehnensteigung genannt). Gesucht sei die Steigung einer Funktionin einem Punkt.Man berechnet zunächst die Steigung derSekanteanüber einem endlichenIntervallder Länge:
- Sekantensteigung =.
Die Sekantensteigung ist also der Quotient zweier Differenzen; sie wird deshalb auchDifferenzenquotientgenannt. Mit der Kurznotationfürkann man die Sekantensteigung abgekürzt alsschreiben. Der Ausdruckverdeutlicht also die beliebig klein werdendeDifferenzzwischen der Stelle, an der abgeleitet werden soll, und einem benachbarten Punkt. In der Literatur wird jedoch, wie auch im Folgenden, in vielen Fällen aus Gründen der Einfachheit das Symbolstattverwendet.
Um eine Tangentensteigung zu berechnen, muss man die beiden Punkte, durch die die Sekante gezogen wird, immer weiter aneinander rücken. Dabei gehen sowohlals auchgegen Null. Der Quotientbleibt aber in vielen Fällen endlich. Auf diesemGrenzübergangberuht die folgende Definition.
Differenzierbarkeit
[Bearbeiten|Quelltext bearbeiten]

Eine Funktion,die einoffenes Intervallin die reellen Zahlen abbildet, heißtdifferenzierbaran der Stelle,falls derGrenzwert
- (mit)
existiert. Dieser Grenzwert heißt Differentialquotient oder Ableitung vonnachan der Stelleund wird als
- oderoderoder
notiert.[25][26]Gesprochen werden diese Notationen als „f Strich von x null “, „d f von x nach d x an der Stelle x gleich x null “, „d f nach d x von x null “respektive „d nach d x von f von x null “. Im später folgenden AbschnittNotationenwerden noch weitere Varianten angeführt, um die Ableitung einer Funktion zu notieren.
Im Laufe der Zeit wurde folgende gleichwertige Definition gefunden, die sich im allgemeineren Kontext komplexer oder mehrdimensionaler Funktionen als leistungsfähiger erwiesen hat: Eine Funktion heißt an einer Stelledifferenzierbar, falls eine Konstanteexistiert, sodass
Der Zuwachs der Funktion,wenn man sich vonnur wenig entfernt, etwa um den Wert,lässt sich also durchsehr gut approximieren. Man nennt deshalb dielineareFunktion,für die alsofür allegilt, auch dieLinearisierungvonan der Stelle.[27]
Eine weitere Definition ist: Es gibt eine an der Stellestetige Funktionmitund eine Konstante,sodass für allegilt
- .
Die Bedingungenund dassan der Stellestetig ist, bedeuten gerade, dass das „Restglied “fürgegengegenkonvergiert.[27]
In beiden Fällen ist die Konstanteeindeutig bestimmt und es gilt.Der Vorteil dieser Formulierung ist, dass Beweise einfacher zu führen sind, da kein Quotient betrachtet werden muss. Diese Darstellung der besten linearen Approximation wurde schon vonKarl Weierstraß,Henri CartanundJean Dieudonnékonsequent angewandt und wird auchWeierstraßsche Zerlegungsformelgenannt.
Bezeichnet man eine Funktion als differenzierbar, ohne sich auf eine bestimmte Stelle zu beziehen, dann bedeutet dies die Differenzierbarkeit an jeder Stelle des Definitionsbereiches, also die Existenz einer eindeutigen Tangente für jeden Punkt des Graphen.
Jede differenzierbare Funktion iststetig,die Umkehrung gilt jedoch nicht.[27]Noch Anfang des 19. Jahrhunderts war man überzeugt, dass eine stetige Funktion höchstens an wenigen Stellen nicht differenzierbar sein könne (wie die Betragsfunktion).Bernard Bolzanokonstruierte dann als erster Mathematiker tatsächlich eine Funktion, die späterBolzanofunktiongenannt wurde, die überall stetig, aber nirgends differenzierbar ist, was in der Fachwelt allerdings nicht bekannt wurde. Karl Weierstraß fand dann in den 1860er Jahren ebenfalls eine derartige Funktion (sieheWeierstraß-Funktion), was diesmal unter Mathematikern Wellen schlug. Ein bekanntes mehrdimensionales Beispiel für eine stetige, nicht differenzierbare Funktion ist die vonHelge von Koch1904 vorgestellteKoch-Kurve.[28]
Ableitungsfunktion
[Bearbeiten|Quelltext bearbeiten]
Die Ableitung der Funktionan der Stelle,bezeichnet mit,beschreibt lokal das Verhalten der Funktion in der Umgebung der betrachteten Stelle.In einigen Fällen ist es möglich, anjedemPunkt desFunktionsgrapheneine Linearisierung vorzunehmen. Dies erlaubt die Definition einerAbleitungsfunktion(oder kurzAbleitung),die jedem Element des Definitionsbereichsder Ausgangsfunktiondie Steigung der dortigen Linearisierung zuordnet. Man sagt in diesem Falle, „ist indifferenzierbar “.[29]
Beispielsweise hat die Quadratfunktionmitan einer beliebigen Stelledie Ableitungdie Quadratfunktion ist also auf der Menge der reellen Zahlen differenzierbar. Die zugehörige Ableitungsfunktionist gegeben durchmit.
Die Ableitungsfunktion ist im Normalfall eine andere Funktion als die ursprünglich betrachtete. Einzige Ausnahme sind die Vielfachender natürlichenExponentialfunktionmit beliebigem– unter denen, wie die Wahlzeigt, auch alle Funktionenmit beliebigementhalten sind (deren Graph aus dem der Exponentialfunktiondurch „seitliche “Verschiebungumentsteht und zu diesem daher kongruent ist).
Ist die Ableitung stetig, dann heißtstetig differenzierbar. In Anlehnung an die Bezeichnungfür die Gesamtheit (denRaum) der stetigen Funktionen mit Definitionsmengewird der Raum der aufstetig differenzierbaren Funktionen mitabgekürzt.[30]
Notationen
[Bearbeiten|Quelltext bearbeiten]Geschichtlich bedingt gibt es unterschiedliche Notationen, um die Ableitung einer Funktion darzustellen.
Lagrange-Notation
[Bearbeiten|Quelltext bearbeiten]In diesem Artikel wurde bisher hauptsächlich die Notationfür die Ableitung vonverwendet. Diese Notation geht auf den MathematikerJoseph-Louis Lagrangezurück, der sie 1797 einführte.[31]Bei dieser Notation wird diezweite Ableitungvonmitund die-te Ableitung mittelsbezeichnet.
Newton-Notation
[Bearbeiten|Quelltext bearbeiten]Isaac Newton– neben Leibniz der Begründer der Differentialrechnung – notierte die erste Ableitung vonmit,entsprechend notierte er diezweite Ableitungdurch.[32]Heutzutage wird diese Schreibweise häufig in der Physik, insbesondere in derMechanik,für dieAbleitung nach der Zeitverwendet.[33]
Leibniz-Notation
[Bearbeiten|Quelltext bearbeiten]Gottfried Wilhelm Leibnizführte für die erste Ableitung von(nach der Variablen) die Notationein.[34]Gelesen wird dieser Ausdruck als „d f von x nach d x “. Für diezweite Ableitungnotierte Leibnizund die-te Ableitung wird mittelsbezeichnet.[35]Bei der Schreibweise von Leibniz handelt es sich nicht um einen Bruch. Die Symboleundwerden „Differentiale“genannt, haben aber in der modernen Differentialrechnung (abgesehen von der Theorie derDifferentialformen) lediglich eine symbolische Bedeutung und sind nur in dieser Schreibweise als formaler Differentialquotient erlaubt. In manchen Anwendungen (Kettenregel,Integration mancherDifferentialgleichungen,Integration durch Substitution) rechnet man mit ihnen aber so, als wären sie gewöhnliche Terme.
Euler-Notation
[Bearbeiten|Quelltext bearbeiten]Die Notationoderfür die erste Ableitung vongeht aufLeonhard Eulerzurück. Dabei wird die Ableitung alsOperator– also als eine besondere Funktion, die selbst auf Funktionen arbeitet, aufgefasst. Diese Idee geht auf den MathematikerLouis François Antoine Arbogastzurück. Diezweite Ableitungwird in dieser Notation mittelsoderund die-te Ableitung durchoderdargestellt.[36]
Ableitungsberechnung
[Bearbeiten|Quelltext bearbeiten]Das Berechnen der Ableitung einer Funktion wirdDifferentiationoderDifferenziationgenannt; sprich, mandifferenziertdiese Funktion.
Um die Ableitungelementarer Funktionen(z. B.,,…) zu berechnen, hält man sich eng an die oben angegebene Definition, berechnet explizit einen Differenzenquotienten und lässt danngegen Null gehen. Dieses Verfahren ist jedoch meistens umständlich. Bei der Lehre der Differentialrechnung wird diese Art der Rechnung daher nur wenige Male vollzogen. Später greift man auf bereits bekannte Ableitungsfunktionen zurück oder schlägt Ableitungen nicht ganz so geläufiger Funktionen in einem Tabellenwerk nach (z. B. imBronstein-Semendjajew,siehe auchTabelle von Ableitungs- und Stammfunktionen) und berechnet die Ableitung zusammengesetzter Funktionen mit Hilfe derAbleitungsregeln.
Ableitungen elementarer Funktionen
[Bearbeiten|Quelltext bearbeiten]Für die Berechnung der Ableitungsfunktion einer elementaren Funktion an einer vorgesehenen Stellewird der zugehörige Differenzenquotient gebildet, der in der Umgebungmitgültig ist, und dann wird der Grenzübergangvollzogen.
Natürliche Potenzen
[Bearbeiten|Quelltext bearbeiten]Der Fallist bereits weiterobenbehandelt worden. Der zugehörige Differenzenquotient ergibt sich zu
Wennist, lässt sichkürzen,
und die Annäherungführt auf
Allgemein für eine natürliche Zahlmitwird derbinomische Lehrsatzherangezogen:
Wennfür alle endlichen Werte vonendlich ist, ist auchendlich. Der in der letzten Gleichung vorstehende Faktorführt auf.Damit entsteht
Zwei Ergänzungen:
- Ein konstanter Summandinkürzt sich inheraus, noch bevor der Grenzübergang vollzogen wird.
- Ein konstanter Faktorinkann inausgeklammert und vor den Bruch gezogen werden.
Exponentialfunktion
[Bearbeiten|Quelltext bearbeiten]
Mit derExponentialfunktionergibt sich der Differenzenquotient
Für jedesgilt
Damit kann im Zählerausgeklammert werden.
Mit demobenhergeleiteten Grenzübergang
entsteht
Darin istdernatürliche Logarithmusvon.Speziell für dieEulersche Zahlist.Damit entsteht die auszeichnende Zusatzeigenschaft
Logarithmus
[Bearbeiten|Quelltext bearbeiten]Mit derLogarithmusfunktionzur Basisergibt sich der Differenzenquotient

Für jedesgilt
Mit demobenhergeleiteten Grenzübergang
und mit derBasisumrechnungentsteht
Dieses existiert nur für.Fürexistiert die Funktion.[37]Mit der Substitutionund derKettenregelergibt ihre Ableitung
Beide Ableitungen können zusammengefasst werden fürzu
Speziell für den natürlichen Logarithmus gilt
Sinus und Kosinus
[Bearbeiten|Quelltext bearbeiten]Mit derSinusfunktionergibt sich der Differenzenquotient
Mit demAdditionstheorem
gilt
Mit demobenhergeleiteten Grenzübergang
und mitentsteht
Für dieKosinusfunktionführt eine entsprechende Rechnung mit
auf
Weitere elementare Funktionen
[Bearbeiten|Quelltext bearbeiten]Mit den vorstehenden Ableitungen können Ableitungsfunktionen für weitere Funktionen aufgestellt werden. Dazu werden zusätzlich die Ableitungsregeln für die Grundrechenarten, dieKettenregelund dieUmkehrregelbenötigt.
Allgemeine Potenzen
[Bearbeiten|Quelltext bearbeiten]Die Funktionist bisher nur fürals natürliche Zahl abgeleitet worden. Die Anwendbarkeit der zugehörigen Ableitungsregel lässt sich beiauf reelle Exponenten erweitern. Mit der Substitution[38]
ist
Wird dieses mit der Kettenregel differenziert, so entsteht das bekannte Ergebnis:
Eine Anwendung ist die Ableitung derWurzelfunktion. Fürgilt mit
Der Fallbetrifft dieQuadratwurzel:
Fürgilt
Tangens und Kotangens
[Bearbeiten|Quelltext bearbeiten]Mit Hilfe derQuotientenregelund den Ableitungsfunktionen für Sinus und Kosinus können auch die Ableitungsfunktionen fürTangens und Kotangensaufgestellt werden. Es gilt
Dabei wurde die als „Trigonometrischer Pythagoras“bezeichnete Formelverwendet. Ebenso wird gewonnen
Arkussinus und Arkuskosinus
[Bearbeiten|Quelltext bearbeiten]Arkussinus und Arkuskosinussind als Umkehrfunktionen vonSinus und Kosinusdefiniert. Die Ableitungen werden mittels der Umkehrregel berechnet. Setzt man,so folgt im Bereich
Für den Arkuskosinus ergibt sich mitebenso
Arkustangens und Arkuskotangens
[Bearbeiten|Quelltext bearbeiten]Arkustangens und Arkuskotangenssind als Umkehrfunktionen vonTangens und Kotangensdefiniert. Setzt man,so folgt mittels der Umkehrregel
Für den Arkuskotangens ergibt sich mitebenso
Zusammengesetzte Funktion
[Bearbeiten|Quelltext bearbeiten]Zusammengesetzte Funktionen lassen sich so weit strukturieren, bis sich zu jedem Strukturelement die jeweils zutreffende elementare Ableitungsregel finden lässt. Dazu gibt es dieSummenregel,dieProduktregel,dieQuotientenregelund dieKettenregel.Da diese in eigenen Artikeln erläutert werden, wird hier nur ein Beispiel vorgestellt.
mit ist ableitbar nachals Potenz mit ist ableitbar nachals Summe mit einer Konstanten mit ist ableitbar nachals trigonometrische Funktion ist ableitbar nachals Potenz mit konstantem Faktor
Nach der Kettenregel ergibt sich
Zusammenfassung
[Bearbeiten|Quelltext bearbeiten]Hier werden die Ableitungsregeln elementarer und zusammengesetzter Funktionen zusammengefasst. Eine ausführliche Liste findet sich unterTabelle von Ableitungs- und Stammfunktionen.
| Anmerkung | ||
|---|---|---|
| Elementares | ||
| konstanter Faktor bleibt erhalten | ||
| konstanter Summand verschwindet | ||
| Potenzfunktion | ||
| Exponentialfunktion | ||
| Logarithmusfunktion | ||
| Trigonometrische Funktionen | ||
| Hyperbelfunktionen | ||
| Summenregel | ||
| Produktregel | ||
| Quotientenregel | ||
oder |
Kettenregel mit | |
oder |
Umkehrregel mitoder nachaufgelöst |
Höhere Ableitungen
[Bearbeiten|Quelltext bearbeiten]Ist die Ableitungeiner Funktionwiederum differenzierbar, so lässt sich die zweite Ableitung vonals Ableitung der ersten definieren. Auf dieselbe Weise können dann auch dritte, vierte etc. Ableitungen definiert werden. Eine Funktion kann dementsprechend einmal differenzierbar, zweimal differenzierbar etc. sein.
Ist die erste Ableitung einesWegesnach der Zeit eineGeschwindigkeit,so kann die zweite Ableitung alsBeschleunigungund die dritte Ableitung alsRuckinterpretiert werden.
Wenn Politiker sich über den „Rückgang des Anstiegs der Arbeitslosenzahl “äußern, dann sprechen sie von der zweiten Ableitung (Änderung des Anstiegs), um die Aussage der ersten Ableitung (Anstieg der Arbeitslosenzahl) zu relativieren.
Höhere Ableitungen können auf verschiedene Weisen geschrieben werden:
oder im physikalischen Fall (bei einer Ableitung nach der Zeit)
Für die formale Bezeichnung beliebiger Ableitungenlegt man außerdemundfest.
Höhere Differentialoperatoren
[Bearbeiten|Quelltext bearbeiten]Isteine natürliche Zahl undoffen, so wird der Raum der in-mal stetig differenzierbaren Funktionen mitbezeichnet. DerDifferentialoperatorinduziert damit eine Kette vonlinearen Abbildungen
und damit allgemein für:
Dabei bezeichnetden Raum der instetigen Funktionen.Exemplarisch: Wird eindurch Anwenden voneinmal abgeleitet, kann das Ergebnisim Allgemeinen nur noch-mal abgeleitet werden usw. Jeder Raumist eine-Algebra,da nach der Summen- bzw. der Produktregel Summen und auch Produkte von-mal stetig differenzierbaren Funktionen wieder-mal stetig differenzierbar sind. Es gilt zudem die aufsteigende Kette von echtenInklusionen
denn offenbar ist jede mindestens-mal stetig differenzierbare Funktion auch-mal stetig differenzierbar usw., jedoch zeigen die Funktionen
exemplarisch Beispiele für Funktionen aus,wenn – wasohne Beschränkung der Allgemeinheitmöglich ist –angenommen wird.[39]
Höhere Ableitungsregeln
[Bearbeiten|Quelltext bearbeiten]Die Ableitung-ter Ordnung für ein Produkt aus zwei-mal differenzierbaren Funktionenundergibt sich aus
- .
Die hier auftretenden Ausdrücke der FormsindBinomialkoeffizienten.Die Formel ist eine Verallgemeinerung der Produktregel.
Diese Formel ermöglicht die geschlossene Darstellung der-ten Ableitung der Komposition zweier-mal differenzierbarer Funktionen. Sie verallgemeinert die Kettenregel auf höhere Ableitungen.
Taylorformeln mit Restglied
[Bearbeiten|Quelltext bearbeiten]Isteine in einem Intervall-mal stetig differenzierbare Funktion, dann gilt für alleundausdie sogenannte Taylorformel:
mit dem-tenTaylorpolynoman der Entwicklungsstelle
und dem-tenRestglied
mit einem.[40]Eine beliebig oft differenzierbare Funktion wirdglatte Funktiongenannt. Da sie alle Ableitungen besitzt, kann die oben angegebene Taylorformel zurTaylorreihevonmit Entwicklungspunkterweitert werden:
Es ist jedoch nicht jede glatte Funktion durch ihre Taylorreihe darstellbar, siehe unten.
Glatte Funktionen
[Bearbeiten|Quelltext bearbeiten]Funktionen, die an jeder Stelle ihres Definitionsbereichsbeliebig oftdifferenzierbar sind, bezeichnet man auch alsglatte Funktionen.Die Menge aller in einer offenen Mengeglatten Funktionenwird meist mitbezeichnet. Sie trägt die Struktur einer-Algebra(skalare Vielfache, Summen und Produkte glatter Funktionen sind wieder glatt) und ist gegeben durch
wobeialle in-mal stetig differenzierbaren Funktionen bezeichnet.[30]Häufig findet man in mathematischen Betrachtungen den Begriffhinreichend glatt.Damit ist gemeint, dass die Funktion mindestens so oft differenzierbar ist, wie es nötig ist, um den aktuellen Gedankengang durchzuführen.
Analytische Funktionen
[Bearbeiten|Quelltext bearbeiten]Der obere Begriff der Glattheit kann weiter verschärft werden. Eine Funktionheißt reell analytisch, wenn sie sich in jedem Punkt lokal in eine Taylorreihe entwickeln lässt, also
für alleund alle hinreichend kleinen Werte von.Analytische Funktionen haben starke Eigenschaften und finden besondere Aufmerksamkeit in der komplexen Analysis. Dort werden dementsprechend keine reell, sondern komplex analytischen Funktionen studiert. Ihre Menge wird meist mitbezeichnet und es gilt.Insbesondere ist jede analytische Funktion glatt, abernicht umgekehrt.Die Existenz aller Ableitungen ist alsonicht hinreichenddafür, dass die Taylorreihe die Funktiondarstellt,wie das folgende Gegenbeispiel
einer nicht analytischen glatten Funktion zeigt.[41]Alle reellen Ableitungen dieser Funktion verschwinden in 0, aber es handelt sich nicht um die Nullfunktion. Daher wird sie an der Stelle 0 nicht durch ihre Taylorreihe dargestellt.
Anwendungen
[Bearbeiten|Quelltext bearbeiten]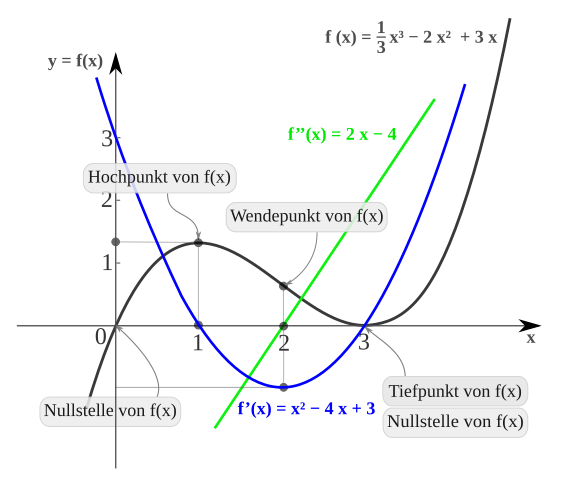
Eine wichtige Anwendung der Differentialrechnung in einer Variablen ist die Bestimmung vonExtremwerten,meist zurOptimierungvon Prozessen, wie etwa im Kontext von Kosten, Material oder Energieaufwand.[42]Die Differentialrechnung stellt eine Methode bereit, Extremstellen zu finden, ohne dabei unter Aufwand numerisch suchen zu müssen. Man macht sich zu Nutze, dass an einer lokalen Extremstellenotwendigerweise die erste Ableitung der Funktiongleich 0 sein muss. Es muss alsogelten, wenneine lokale Extremstelle ist. Allerdings bedeutet andersherumnoch nicht, dass es sich beium ein Maximum oder Minimum handelt. In diesem Fall werden mehr Informationen benötigt, um eine eindeutige Entscheidung treffen zu können, was meist durch Betrachten höherer Ableitungen beimöglich ist.
Eine Funktion kann einen Maximal- oder Minimalwert haben, ohne dass die Ableitung an dieser Stelle existiert, jedoch kann in diesem Falle die Differentialrechnung nicht verwendet werden. Im Folgenden werden daher nur zumindest lokal differenzierbare Funktionen betrachtet. Als Beispiel nehmen wir diePolynomfunktionmit dem Funktionsterm
Die Abbildung zeigt den Verlauf der Graphen von,und.
Horizontale Tangenten
[Bearbeiten|Quelltext bearbeiten]Besitzt eine Funktionmitan einer Stelleihren größten Wert, gilt also für alledieses Intervalls,und istan der Stelledifferenzierbar, so kann die Ableitung dort nur gleich Null sein:.Eine entsprechende Aussage gilt, fallsinden kleinsten Wert annimmt.
Geometrische Deutung diesesSatzes von Fermatist, dass der Graph der Funktion in lokalen Extrempunkten eine parallel zur-Achse verlaufende Tangente, auch waagerechte Tangente genannt, besitzt.
Es ist somit für differenzierbare Funktionen einenotwendige Bedingungfür das Vorliegen einer Extremstelle, dass die Ableitung an der betreffenden Stelle den Wert 0 annimmt:
Umgekehrt kann aber daraus, dass die Ableitung an einer Stelle den Wert Null hat, noch nicht auf eine Extremstelle geschlossen werden, es könnte auch beispielsweise einSattelpunktvorliegen. Eine Liste verschiedener hinreichender Kriterien, deren Erfüllung sicher auf eine Extremstelle schließen lässt, findet sich im ArtikelExtremwert.Diese Kriterien benutzen meist die zweite oder noch höhere Ableitungen.
Bedingung im Beispiel
[Bearbeiten|Quelltext bearbeiten]Im Beispiel ist
Daraus folgt, dassgenau fürundgilt. Die Funktionswerte an diesen Stellen sindund,d. h., die Kurve hat in den Punktenundwaagerechte Tangenten, und nur in diesen.
Da die Folge
abwechselnd aus kleinen und großen Werten besteht, muss in diesem Bereich ein Hoch- und ein Tiefpunkt liegen. Nach dem Satz von Fermat hat die Kurve in diesen Punkten eine waagerechte Tangente, es kommen also nur die oben ermittelten Punkte in Frage: Also istein Hochpunkt undein Tiefpunkt.
Kurvendiskussion
[Bearbeiten|Quelltext bearbeiten]Mit Hilfe der Ableitungen lassen sich noch weitere Eigenschaften der Funktion analysieren, wie die Existenz vonWende-undSattelpunkten,dieKonvexitätoder die oben schon angesprocheneMonotonie.Die Durchführung dieser Untersuchungen ist Gegenstand der Kurvendiskussion.
Termumformungen
[Bearbeiten|Quelltext bearbeiten]Neben der Bestimmung der Steigung von Funktionen ist die Differentialrechnung durch ihrenKalkülein wesentliches Hilfsmittel bei derTermumformung.Hierbei löst man sich von jeglichem Zusammenhang mit der ursprünglichen Bedeutung der Ableitung als Anstieg. Hat man zweiTermeals gleich erkannt, lassen sich durch Differentiation daraus weitere (gesuchte) Identitäten gewinnen. Ein Beispiel mag dies verdeutlichen:
Aus der bekannten Partialsumme
dergeometrischen Reihesoll die Summe
berechnet werden. Dies gelingt durch Differentiation mit Hilfe derQuotientenregel:
Alternativ ergibt sich die Identität auch durch Ausmultiplizieren und anschließendes dreifachesTeleskopieren,was aber nicht so einfach zu durchschauen ist.
Zentrale Aussagen der Differentialrechnung einer Variablen
[Bearbeiten|Quelltext bearbeiten]Fundamentalsatz der Analysis
[Bearbeiten|Quelltext bearbeiten]Die wesentliche Leistung Leibniz’ war die Erkenntnis, dassIntegrationund Differentiation zusammenhängen. Diese formulierte er im Hauptsatz der Differential- und Integralrechnung, auchFundamentalsatz der Analysisgenannt, der besagt:
Istein Intervall,eine stetige Funktion undeine beliebige Zahl aus,so ist die Funktion
stetig differenzierbar, und ihre Ableitungist gleich.
Hiermit ist also eine Anleitung zum Integrieren gegeben: Gesucht ist eine Funktion,deren Ableitungder Integrandist. Dann gilt:[43]
Mittelwertsatz der Differentialrechnung
[Bearbeiten|Quelltext bearbeiten]Ein weiterer zentraler Satz der Differentialrechnung ist derMittelwertsatz,der 1821 vonCauchybewiesen wurde.[44]
Es seieine Funktion, die auf dem abgeschlossenen Intervall(mit) definiert und stetig ist. Außerdem sei die Funktionim offenen Intervalldifferenzierbar. Unter diesen Voraussetzungen gibt es mindestens ein,sodass
gilt – geometrisch-anschaulich: Zwischen zwei Schnittpunkten einerSekantegibt es auf der Kurve einen Punkt mit zur Sekante parallelerTangente.[45]
Monotonie und Differenzierbarkeit
[Bearbeiten|Quelltext bearbeiten]Istundeine differenzierbare Funktion mitfür alle,so gelten folgende Aussagen:[46]
- Die Funktionist striktmonoton.
- Es istmit irgendwelchen.
- Die Umkehrfunktionexistiert, ist differenzierbar und erfüllt.
Daraus lässt sich herleiten, dass eine stetig differenzierbare Funktion,deren Ableitung nirgends verschwindet, bereits einenDiffeomorphismuszwischen den Intervallenunddefiniert. In mehreren Variablen ist die analoge Aussage falsch. So verschwindet die Ableitung derkomplexen Exponentialfunktion,nämlich sie selbst, in keinem Punkt, aber es handelt sich um keine (global)injektive Abbildung.Man beachte, dass diese als höherdimensionale reelle Funktionaufgefasst werden kann, daein zweidimensionaler-Vektorraumist.
Allerdings liefert derSatz von Hadamardein Kriterium, mit dem in manchen Fällen gezeigt werden kann, dass eine stetig differenzierbare FunktioneinHomöomorphismusist.
Die Regel von de L’Hospital
[Bearbeiten|Quelltext bearbeiten]Als eine Anwendung desMittelwertsatzeslässt sich eine Beziehung herleiten, die es in manchen Fällen erlaubt, unbestimmte Terme der Gestaltoderzu berechnen.[47]
Seiendifferenzierbar undhabe keine Nullstelle. Ferner gelte entweder
oder
- .
Dann gilt
unter der Bedingung, dass der letzteGrenzwertinexistiert.
Differentialrechnung bei Funktionenfolgen und Integralen
[Bearbeiten|Quelltext bearbeiten]In vielen analytischen Anwendungen hat man es nicht miteinerFunktion,sondern mit einer Folgezu tun. Dabei muss geklärt werden, inwieweit sich der Ableitungsoperator mit Prozessen wie Grenzwerten, Summen oder Integralen verträgt.
Grenzfunktionen
[Bearbeiten|Quelltext bearbeiten]Bei einer konvergenten, differenzierbaren Funktionenfolgeist es im Allgemeinen nicht möglich, Rückschlüsse auf den Grenzwert der Folgezu ziehen, selbst dann nicht, wenngleichmäßig konvergiert.Die analoge Aussage in der Integralrechnung ist hingegen richtig: Bei gleichmäßiger Konvergenz können Limes und Integral vertauscht werden, zumindest dann, wenn die Grenzfunktion „gutartig “ist.
Aus dieser Tatsache kann zumindest Folgendes geschlossen werden: Seieine Folge stetig differenzierbarer Funktionen, sodass die Folge der Ableitungengleichmäßiggegen eine Funktionkonvergiert. Es gelte außerdem, dass die Folgefürmindestens einenPunktkonvergiert. Dann konvergiertbereits gleichmäßig gegen eine differenzierbare Funktionund es gilt.[48]
Vertauschen mit unendlichen Reihen
[Bearbeiten|Quelltext bearbeiten]Seieine Folge stetig differenzierbarer Funktionen, sodass die Reihekonvergiert, wobeidieSupremumsnormbezeichnet. Konvergiert außerdem die Reihefür ein,dann konvergiert die Funktionenreihegleichmäßig gegen eine differenzierbare Funktion, und es gilt[49]
Das Resultat geht aufKarl Weierstraßzurück.[50]
Vertauschen mit Integration
[Bearbeiten|Quelltext bearbeiten]Es seieine stetige Funktion, sodass diepartielle Ableitung
existiert und stetig ist. Dann ist auch
differenzierbar, und es gilt
Diese Regel wird auch alsLeibnizsche Regelbezeichnet.[51]
Differentialrechnung über den komplexen Zahlen
[Bearbeiten|Quelltext bearbeiten]Bisher wurde nur vonreellenFunktionen gesprochen. Alle behandelten Regeln lassen sich jedoch auf Funktionen mitkomplexenEingaben und Werten übertragen. Dies hat den Hintergrund, dass die komplexen Zahlengenau wie die reellen Zahlen einenKörperbilden, dort also Addition, Multiplikation und Division erklärt ist. Diese zusätzliche Struktur bildet den entscheidenden Unterschied zu einer Herangehensweise mehrdimensionaler reeller Ableitungen, wennbloß als zweidimensionaler-Vektorraumaufgefasst wird. Ferner lassen sich die euklidischen Abstandsbegriffe der reellen Zahlen (siehe auchEuklidischer Raum) auf natürliche Weise auf komplexe Zahlen übertragen. Dies erlaubt eine analoge Definition und Behandlung der für die Differentialrechnung wichtigen Begriffe wieFolgeundGrenzwert.[52]
Ist alsooffen,eine komplexwertige Funktion, so heißtan der Stellekomplex differenzierbar,wenn der Grenzwert
existiert.[53]Dieser wird mitbezeichnet und(komplexe) Ableitung vonan der Stellegenannt. Es ist demnach möglich, den Begriff der Linearisierung ins Komplexe weiterzutragen: Die Ableitungist die „Steigung “der linearen Funktion, diebeioptimal approximiert. Allerdings ist darauf zu achten, dass der Wertim Grenzwert nicht nur reelle, sondern auch komplexe Zahlen (nahe bei 0) annehmen kann. Dies hat zur Folge, dass der Terminus der komplexen Differenzierbarkeit wesentlich restriktiver ist als jener der reellen Differenzierbarkeit. Während im Reellen nur zwei Richtungen im Differenzenquotienten betrachtet werden mussten, sind es im Komplexen unendlich viele Richtungen, da diese keine Gerade, sondern eine Ebene aufspannen. So ist beispielsweise die Betragsfunktionnirgends komplex differenzierbar. Eine komplexe Funktion ist genau dann komplex differenzierbar in einem Punkt, wenn sie dort dieCauchy-Riemannschen Differentialgleichungenerfüllt undtotal differenzierbarist.[54]
Trotz (bzw. gerade wegen) des viel einschränkenderen Begriffs der komplexen Differenzierbarkeit übertragen sich alle üblichen Rechenregeln der reellen Differentialrechnung in die komplexe Differentialrechnung. Dazu gehören die Ableitungsregeln, also zum Beispiel Summen-, Produkt- und Kettenregel, wie auch die Umkehrregel für inverse Funktionen. Viele Funktionen, wie Potenzen, die Exponentialfunktion oder der Logarithmus, haben natürliche Fortsetzungen in die komplexen Zahlen und besitzen weiterhin ihre charakteristischen Eigenschaften. Von diesem Gesichtspunkt her ist die komplexe Differentialrechnung mit ihrem reellen Analogon identisch.
Wenn eine Funktionin ganzkomplex differenzierbar ist, nennt man sie auch eineinholomorphe Funktion.[55]Holomorphe Funktionen haben bedeutende Eigenschaften. So ist zum Beispiel jede holomorphe Funktion bereits (in jedem Punkt) beliebig oft differenzierbar. Die daraus aufkommende Klassifizierungfrage holomorpher Funktionen ist Gegenstand derFunktionentheorie.Es stellt sich heraus, dass im komplex-eindimensionalen Fall der Begriff holomorph äquivalent zum Begriffanalytischist. Demnach ist jede holomorphe Funktion analytisch, und umgekehrt. Ist eine Funktion sogar in ganzholomorph, so nennt man sieganz.Beispiele für ganze Funktionen sind die Potenzfunktionenmit natürlichen Zahlensowie,und.
Differentialrechnung mehrdimensionaler Funktionen
[Bearbeiten|Quelltext bearbeiten]Alle vorherigen Ausführungen legten eine Funktion ineinerVariablen (also mit einer reellen oder komplexen Zahl als Argument) zugrunde. Funktionen, dieVektorenauf Vektoren oder Vektoren auf Zahlen abbilden, können ebenfalls eine Ableitung haben. Allerdings ist eine Tangente an den Funktionsgraph in diesen Fällen nicht mehr eindeutig bestimmt, da es viele verschiedene Richtungen gibt. Hier ist also eine Erweiterung des bisherigen Ableitungsbegriffs notwendig.
Mehrdimensionale Differenzierbarkeit und die Jacobi-Matrix
[Bearbeiten|Quelltext bearbeiten]Richtungsableitung
[Bearbeiten|Quelltext bearbeiten]Es seioffen,eine Funktion,undein (Richtungs-)Vektor. Aufgrund der Offenheit vongibt es einmitfür alle,weshalb die Funktionmitwohldefiniert ist. Ist diese Funktion indifferenzierbar, so heißt ihre AbleitungRichtungsableitungvonan der Stellein der Richtungund wird meistens mitbezeichnet.[56]Es gilt:
Es besteht ein Zusammenhang zwischen der Richtungsableitung und der Jacobi-Matrix. Istdifferenzierbar, dann existiertund es gilt in einer Umgebung von:
wobei die Schreibweisedas entsprechendeLandau-Symbolbezeichnet.[57]
Es werde als Beispiel eine Funktionbetrachtet, also einSkalarfeld.Diese könnte eineTemperaturfunktionsein: In Abhängigkeit vom Ort wird die Temperatur im Zimmer gemessen, um zu beurteilen, wie effektiv die Heizung ist. Wird dasThermometerin eine bestimmte Raumrichtung bewegt, ist eine Veränderung der Temperatur festzustellen. Dies entspricht genau der entsprechenden Richtungsableitung.
Partielle Ableitungen
[Bearbeiten|Quelltext bearbeiten]Die Richtungsableitungen in spezielle Richtungen,nämlich in die der Koordinatenachsen mit der Länge,nennt man diepartiellen Ableitungen.
Insgesamt lassen sich für eine Funktion inVariablenpartielle Ableitungen errechnen:[58]
Die einzelnen partiellen Ableitungen einer Funktion lassen sich auch gebündelt alsGradientoderNablavektoranschreiben:[59]
Meist wird der Gradient alsZeilenvektor(also „liegend “) geschrieben. In manchen Anwendungen, besonders in der Physik, ist jedoch auch die Schreibweise alsSpaltenvektor(also „stehend “) üblich. Partielle Ableitungen können selbst differenzierbar sein und ihre partiellen Ableitungen lassen sich dann in der sogenanntenHesse-Matrixanordnen.
Totale Differenzierbarkeit
[Bearbeiten|Quelltext bearbeiten]Eine Funktionmit,wobeieineoffene Mengeist, heißt in einem Punkttotal differenzierbar(oder auch nurdifferenzierbar,manchmal auchFréchet-differenzierbar[56]), falls einelineare Abbildungexistiert, sodass
gilt.[60]Für den eindimensionalen Fall stimmt diese Definition mit der oben angegebenen überein. Die lineare Abbildungist bei Existenz eindeutig bestimmt, ist also insbesondere unabhängig von der Wahläquivalenter Normen.Die Tangente wird daher durch die lokale Linearisierung der Funktion abstrahiert. Die Matrixdarstellung der ersten Ableitung vonnennt manJacobi-Matrix.Es handelt sich um eine-Matrix. Fürerhält man denweiter obenbeschriebenen Gradienten.
Zwischen den partiellen Ableitungen und der totalen Ableitung besteht folgender Zusammenhang: Existiert in einem Punkt die totale Ableitung, so existieren dort auch alle partiellen Ableitungen. In diesem Fall stimmen die partiellen Ableitungen mit den Koeffizienten der Jacobi-Matrix überein:
Umgekehrt folgt aus der Existenz der partiellen Ableitungen in einem Punktnicht zwingend die totale Differenzierbarkeit, ja nicht einmal die Stetigkeit. Sind die partiellen Ableitungen jedoch zusätzlich in einer Umgebung vonstetig,dann ist die Funktion inauch total differenzierbar.[61]
Rechenregeln der mehrdimensionalen Differentialrechnung
[Bearbeiten|Quelltext bearbeiten]Kettenregel
[Bearbeiten|Quelltext bearbeiten]Es seienundoffen sowieundinbzw.differenzierbar, wobei.Dann istmitindifferenzierbar mit Jacobi-Matrix
Mit anderen Worten, die Jacobi-Matrix der Kompositionist das Produkt der Jacobi-Matrizen vonund.[62]Es ist zu beachten, dass die Reihenfolge der Faktoren im Gegensatz zum klassischen eindimensionalen Fall eine Rolle spielt.
Produktregel
[Bearbeiten|Quelltext bearbeiten]Mit Hilfe der Kettenregel kann die Produktregel aufreellwertigeFunktionen mit höherdimensionalem Definitionsbereich verallgemeinert werden.[63]Istoffen und sindbeide indifferenzierbar, so folgt
oder in der Gradientenschreibweise
Funktionenfolgen
[Bearbeiten|Quelltext bearbeiten]Seioffen. Es bezeichneeine Folge stetig differenzierbarer Funktionen,sodass es Funktionenundgibt (dabei istder Raum der linearen Abbildungen vonnach), sodass Folgendes gilt:
- konvergiert punktweise gegen,
- konvergiert lokal gleichmäßig gegen.
Dann iststetig differenzierbar aufund es gilt.[64]
Implizite Differentiation
[Bearbeiten|Quelltext bearbeiten]Ist eine Funktiondurch eine implizite Gleichunggegeben, so folgt aus dermehrdimensionalen Kettenregel,die für Funktionen mehrerer Variablen gilt,
Für die Ableitung der Funktionergibt sich daher
mitund
Zentrale Sätze der Differentialrechnung mehrerer Veränderlicher
[Bearbeiten|Quelltext bearbeiten]Satz von Schwarz
[Bearbeiten|Quelltext bearbeiten]Die Differentiationsreihenfolge ist bei der Berechnung partieller Ableitungen höherer Ordnung unerheblich, wenn alle partiellen Ableitungen bis zu dieser Ordnung (einschließlich) stetig sind. Dies bedeutet konkret: Istoffen und die Funktionzweimal stetig differenzierbar (d. h., alle zweifachen partiellen Ableitungen existieren und sind stetig), so gilt für alleund:
Der Satz wird falsch, wenn die Stetigkeit der zweifachen partiellen Ableitungen weggelassen wird.[65]
Satz von der impliziten Funktion
[Bearbeiten|Quelltext bearbeiten]Der Satz von der impliziten Funktion besagt, dass Funktionsgleichungen auflösbar sind, falls dieJacobi-Matrixbezüglich bestimmter Variablen lokal invertierbar ist.[66]
Mittelwertsatz
[Bearbeiten|Quelltext bearbeiten]Über den höherdimensionalen Mittelwertsatz gelingt es, eine Funktion entlang einer Verbindungsstrecke abzuschätzen, wenn die dortigen Ableitungen bekannt sind. Seienoffen unddifferenzierbar. Gegeben seien zudem zwei Punkte,sodass die Verbindungsstreckeeine Teilmenge vonist. Dann postuliert der Mittelwertsatz die Ungleichung:[67]
Eine präzisere Aussage ist indes für den FallreellwertigerFunktionen in mehreren Veränderlichen möglich, siehe auchMittelwertsatz für reellwertige Funktionen mehrerer Variablen.
Höhere Ableitungen im Mehrdimensionalen
[Bearbeiten|Quelltext bearbeiten]Auch im Fall höherdimensionaler Funktionen können höhere Ableitungen betrachtet werden. Die Konzepte haben jedoch einige starke Unterschiede zum klassischen Fall, die besonders im Falle mehrerer Veränderlicher in Erscheinung treten. Bereits die Jacobi-Matrix lässt erkennen, dass die Ableitung einer höherdimensionalen Funktion an einer Stelle nicht mehr die gleiche Gestalt wie der dortige Funktionswert haben muss. Wird nun die erste Ableitungerneut abgeleitet, so ist die erneute „Jacobi-Matrix “im Allgemeinen ein noch umfangreicheres Objekt. Für dessen Beschreibung ist das Konzept dermultilinearen Abbildungenbzw. desTensorserforderlich. Ist,so ordnetjedem Punkt eine-Matrix (lineare Abbildung vonnach) zu. Induktiv definiert man für die höheren Ableitungen
wobeider Raum der-multilinearen Abbildungen vonnachbezeichnet. Analog wie im eindimensionalen Fall definiert man die Räume der-mal stetig differenzierbaren Funktionen aufdurch,und die glatten Funktion via[68]
Auch die Konzepte der Taylor-Formeln und der Taylorreihe lassen sich auf den höherdimensionalen Fall verallgemeinern, siehe auchTaylor-Formel im Mehrdimensionalenbzw.mehrdimensionale Taylorreihe.
Anwendungen
[Bearbeiten|Quelltext bearbeiten]Fehlerrechnung
[Bearbeiten|Quelltext bearbeiten]Ein Anwendungsbeispiel der Differentialrechnung mehrerer Veränderlicher betrifft dieFehlerrechnung,zum Beispiel im Kontext derExperimentalphysik.Während man im einfachsten Falle die zu bestimmende Größe direkt messen kann, wird es meistens der Fall sein, dass sie sich durch einen funktionalen Zusammenhang aus einfacher zu messenden Größen ergibt. Typischerweise hat jede Messung eine gewisse Unsicherheit, die man durch Angabe desMessfehlerszu quantifizieren versucht.[69]
Bezeichnet zum Beispielmitdas Volumen einesQuaders,so könnte das Ergebnisexperimentell ermittelt werden, indem man Länge,Breiteund Höheeinzeln misst. Treten bei diesen die Fehler,undauf, so gilt für den Fehler in der Volumenberechnung:
Allgemein gilt, dass wenn eine zu messende Größe funktional von einzeln gemessenen Größendurchabhängt und bei deren Messungen jeweils die Fehlerentstehen, der Fehler der daraus errechneten Größe ungefähr bei
liegen wird. Dabei bezeichnet der Vektordie exakten Terme der einzelnen Messungen.[69]
Lösungsnäherung von Gleichungssystemen
[Bearbeiten|Quelltext bearbeiten]Viele höhere Gleichungssysteme lassen sich nicht algebraisch geschlossen lösen. In manchen Fällen kann man aber zumindest eine ungefähre Lösung ermitteln. Ist das System durchgegeben, mit einer stetig differenzierbaren Funktion,so konvergiert die Iterationsvorschrift
unter gewissen Voraussetzungen gegen eine Nullstelle. Dabei bezeichnetdasInverseder Jacobi-Matrix zu.Der Prozess stellt eine Verallgemeinerung des klassischen eindimensionalenNewton-Verfahrensdar. Aufwendig ist allerdings die Berechnung dieser Inversen in jedem Schritt. Unter Verschlechterung der Konvergenzrate kann in manchen Fällen die Modifikationstattvorgenommen werden, womit nur eine Matrix invertiert werden muss.[70]
Extremwertaufgaben
[Bearbeiten|Quelltext bearbeiten]Auch für die Kurvendiskussion von Funktionenist die Auffindung von Minima bzw. Maxima, zusammengefasstExtrema,ein wesentliches Anliegen. Die mehrdimensionale Differentialrechnung liefert Möglichkeiten, diese zu bestimmen, sofern die betrachtete Funktion zweimal stetig differenzierbar ist. Analog zum Eindimensionalen besagt die notwendige Bedingung für die Existenz für Extrema, dass im besagten Punktalle partiellen Ableitungen 0 sein müssen, also
für alle.Dieses Kriterium ist nicht hinreichend, dient aber dazu, diesekritischen Punkteals mögliche Kandidaten für Extrema zu ermitteln. Unter Bestimmung der Hesse-Matrix, der zweiten Ableitung, kann anschließend in manchen Fällen entschieden werden, um welche Art Extremstelle es sich handelt.[71]Im Gegensatz zum Eindimensionalen ist die Formenvielfalt kritischer Punkte größer. Mittels einerHauptachsentransformation,also einer detaillierten Untersuchung der Eigenwerte, der durch eine mehrdimensionale Taylor-Entwicklung im betrachteten Punkt gegebenenquadratischen Formlassen sich die verschiedenen Fälle klassifizieren.[72]
Optimierung unter Nebenbedingungen
[Bearbeiten|Quelltext bearbeiten]Häufig ist bei Optimierungsproblemen die Zielfunktionlediglich auf einerTeilmengezu minimieren, wobeidurch sog.Nebenbedingungenbzw.Restriktionenbestimmt ist. Ein Verfahren, das zur Lösung solcher Probleme herangezogen werden kann, ist dieLagrangesche Multiplikatorregel.[73]Diese nutzt die mehrdimensionale Differentialrechnung und lässt sich sogar auf Ungleichungsnebenbedingungen ausweiten.[74]
Beispiel aus der Mikroökonomie
[Bearbeiten|Quelltext bearbeiten]
In derMikroökonomiewerden beispielsweise verschiedene Arten vonProduktionsfunktionenanalysiert, um daraus Erkenntnisse fürmakroökonomischeZusammenhänge zu gewinnen. Hier ist vor allem das typische Verhalten einer Produktionsfunktion von Interesse: Wie reagiert die abhängige VariableOutput(z. B. Output einer Volkswirtschaft), wenn dieInputfaktoren(hier:ArbeitundKapital) um eine infinitesimal kleine Einheit erhöht werden?
Ein Grundtyp einer Produktionsfunktion ist etwa dieneoklassische Produktionsfunktion.Sie zeichnet sich unter anderem dadurch aus, dass der Output bei jedem zusätzlichen Input steigt, dass aber die Zuwächse abnehmend sind. Es sei beispielsweise für eine Volkswirtschaft dieCobb-Douglas-Funktion
- mit
maßgebend. Zu jedem Zeitpunkt wird in der Volkswirtschaft unter dem Einsatz der Produktionsfaktoren Arbeitund Kapitalmithilfe eines gegebenen TechnologielevelsOutput produziert. Die erste Ableitung dieser Funktion nach den Produktionsfaktoren ergibt:
- .
Da die partiellen Ableitungen aufgrund der Beschränkungnur positiv werden können, sieht man, dass der Output bei einer Erhöhung der jeweiligen Inputfaktoren steigt. Die partiellen Ableitungen 2. Ordnung ergeben:
- .
Sie werden für alle Inputs negativ sein, also fallen die Zuwachsraten. Man könnte also sagen, dass bei steigendem Input der Output unterproportionalsteigt. Dierelative Änderungdes Outputs im Verhältnis zu einer relativen Änderung des Inputs ist hier durch dieElastizitätgegeben. Vorliegend bezeichnetdie Produktionselastizität des Kapitals, die bei dieser Produktionsfunktion dem Exponentenentspricht, der wiederum die Kapitaleinkommensquote repräsentiert. Folglich steigt der Output bei einer infinitesimal kleinen Erhöhung des Kapitals um die Kapitaleinkommensquote.
Weiterführende Theorien
[Bearbeiten|Quelltext bearbeiten]Differentialgleichungen
[Bearbeiten|Quelltext bearbeiten]Eine wichtige Anwendung der Differentialrechnung besteht in dermathematischen Modellierungphysikalischer Vorgänge. Wachstum, Bewegung oder Kräfte haben alle mit Ableitungen zu tun, ihre formelhafte Beschreibung muss also Differentiale enthalten. Typischerweise führt dies auf Gleichungen, in denen Ableitungen einer unbekannten Funktion auftauchen, sogenannteDifferentialgleichungen.
Beispielsweise verknüpft dasnewtonsche Bewegungsgesetz
die Beschleunigungeines Körpers mit seiner Masseund der auf ihn einwirkenden Kraft.Das Grundproblem der Mechanik lautet deshalb, aus einer gegebenen Beschleunigung dieOrtsfunktioneines Körpers herzuleiten. Diese Aufgabe, eine Umkehrung der zweifachen Differentiation, hat die mathematische Gestalt einer Differentialgleichung zweiter Ordnung. Die mathematische Schwierigkeit dieses Problems rührt daher, dass Ort, Geschwindigkeit und BeschleunigungVektorensind, die im Allgemeinen nicht in die gleiche Richtung zeigen, und dass die Kraft von der Zeitund vom Ortabhängen kann.
Da viele Modelle mehrdimensional sind, sind bei der Formulierung häufig die weiter oben erklärten partiellen Ableitungen sehr wichtig, mit denen sichpartielle Differentialgleichungenformulieren lassen. Mathematisch kompakt werden diese mittelsDifferentialoperatorenbeschrieben und analysiert.
Differentialgeometrie
[Bearbeiten|Quelltext bearbeiten]Zentrales Thema der Differentialgeometrie ist die Ausdehnung der klassischen Analysis auf höhere geometrische Objekte. Diese sehen lokal so aus wie zum Beispiel der euklidische Raum,können aber global eine andere Gestalt haben. Der Begriff hinter diesem Phänomen ist dieMannigfaltigkeit.Mit Hilfe der Differentialgeometrie werden Fragestellungen über die Natur solcher Objekte studiert – zentrales Werkzeug ist weiterhin die Differentialrechnung. Gegenstand der Untersuchung sind oftmals die Abstände zwischen Punkten oder die Volumina von Figuren. Beispielsweise kann mit ihrer Hilfe der kürzestmögliche Weg zwischen zwei Punkten auf einer gekrümmten Fläche bestimmt und gemessen werden, die sogenannteGeodätische.Für die Messung von Volumina wird der Begriff derDifferentialformbenötigt. Differentialformen erlauben unter anderem eine koordinatenunabhängigeIntegration.
Sowohl die theoretischen Ergebnisse als auch Methoden der Differentialgeometrie haben bedeutende Anwendungen in derPhysik.So beschriebAlbert EinsteinseineRelativitätstheoriemit differentialgeometrischen Begriffen.
Verallgemeinerungen
[Bearbeiten|Quelltext bearbeiten]In vielen Anwendungen ist es wünschenswert, Ableitungen auch für stetige oder sogar unstetige Funktionen bilden zu können. So kann beispielsweise eine sich am Strand brechende Welle durch eine partielle Differentialgleichung modelliert werden, die Funktion der Höhe der Welle ist aber noch nicht einmal stetig. Zu diesem Zweck verallgemeinerte man Mitte des 20. Jahrhunderts den Ableitungsbegriff auf den Raum derDistributionenund definierte dort eineschwache Ableitung.Eng verbunden damit ist der Begriff desSobolew-Raums.
Der Begriff der Ableitung als Linearisierung lässt sich analog auf Funktionenzwischen zweinormierbarentopologischen Vektorräumenundübertragen (s. HauptartikelFréchet-Ableitung,Gâteaux-Differential,Lorch-Ableitung):heißt inFréchet-differenzierbar,wenn ein stetigerlinearer Operatorexistiert, sodass
- .
Eine Übertragung des Begriffes der Ableitung auf andere Ringe alsund(und Algebren darüber) führt zurDerivation.
Siehe auch
[Bearbeiten|Quelltext bearbeiten]Literatur
[Bearbeiten|Quelltext bearbeiten]Differentialrechnung ist ein zentraler Unterrichtsgegenstand in derSekundarstufe IIund wird somit in allen Mathematik-Lehrbüchern dieser Stufe behandelt.
Lehrbücher für Mathematik-Studierende
[Bearbeiten|Quelltext bearbeiten]- Henri Cartan:Differentialrechnung.Bibliographisches Institut, Mannheim 1974,ISBN 3-411-01442-3.
- Henri Cartan:Differentialformen.Bibliographisches Institut, Mannheim 1974,ISBN 3-411-01443-1.
- Henri Cartan:Elementare Theorien der analytischen Funktionen einer und mehrerer komplexen Veränderlichen.Bibliographisches Institut, Mannheim 1966, 1981,ISBN 3-411-00112-7.
- Richard Courant:Vorlesungen über Differential- und Integralrechnung.2 Bände. Springer 1928, 4. Auflage 1971,ISBN 3-540-02956-7.
- Jean Dieudonné:Grundzüge der modernen Analysis.Band 1. Vieweg, Braunschweig 1972,ISBN 3-528-18290-3.
- Gregor M. Fichtenholz:Differential- und Integralrechnung I–III.Verlag Harri Deutsch, Frankfurt am Main 1990–2004,ISBN 978-3-8171-1418-4(kompletter Satz).
- Otto Forster:Analysis 1. Differential- und Integralrechnung einer Veränderlichen.7. Auflage. Vieweg, Braunschweig 2004,ISBN 3-528-67224-2.
- Otto Forster:Analysis 2. Differentialrechnung im.Gewöhnliche Differentialgleichungen.6. Auflage. Vieweg, Braunschweig 2005,ISBN 3-528-47231-6.
- Konrad Königsberger:Analysis.2 Bände. Springer, Berlin 2004,ISBN 3-540-41282-4.
- Wladimir I. Smirnow:Lehrgang der höheren Mathematik(Teil 1–5).Verlag Harri Deutsch, Frankfurt am Main, 1995–2004,ISBN 978-3-8171-1419-1(kompletter Satz).
- Steffen Timmann:Repetitorium der Analysis.2 Bände. Binomi, Springe 1993,ISBN 3-923923-50-3,ISBN 3-923923-52-X.
- Serge Lang:A First Course in Calculus.Fifth Edition, Springer,ISBN 0-387-96201-8.
Lehrbücher für das Grundlagenfach Mathematik
[Bearbeiten|Quelltext bearbeiten]- Rainer Ansorge,Hans Joachim Oberle:Mathematik für Ingenieure.Band 1. Akademie-Verlag, Berlin 1994, 3. Auflage 2000,ISBN 3-527-40309-4.
- Günter Bärwolff(unter Mitarbeit von G. Seifert):Höhere Mathematik für Naturwissenschaftler und Ingenieure.Elsevier Spektrum Akademischer Verlag, München 2006,ISBN 3-8274-1688-4.
- Lothar Papula:Mathematik für Naturwissenschaftler und Ingenieure.Band 1. Vieweg, Wiesbaden 2004,ISBN 3-528-44355-3.
- Klaus Weltner:Mathematik für Physiker 1.Springer, Berlin 2011,ISBN 978-3-642-15527-7.
- Peter Dörsam:Mathematik anschaulich dargestellt für Studierende der Wirtschaftswissenschaften.15. Auflage. PD-Verlag, Heidenau 2010,ISBN 978-3-86707-015-7.
Weblinks
[Bearbeiten|Quelltext bearbeiten]- Tool zur Bestimmung von Ableitungen beliebiger Funktionen mit einer oder mehreren Variablen mit Rechenweg (deutsch; benötigt JavaScript)
- Online-Rechner zum Ableiten von Funktionen mit Rechenweg und Erklärungen (deutsch)
- Anschauliche Erklärung von Ableitungen
- Beispiele zu jeder Ableitungsregel
Einzelnachweise
[Bearbeiten|Quelltext bearbeiten]- ↑Herbert Amann,Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 316.
- ↑Serge Lang:A First Course in Calculus.Fifth Edition. Springer, S. 59–61.
- ↑Fritz Wicke:Einführung in die Höhere Mathematik: unter besonderer Berücksichtigung der Bedürfnisse des Ingenieurs.Band 1. Springer, 1927, Seite 103.
- ↑Carl Spitz:Erster Cursus der Differential- und Integralrechnung.C. F. Winter’sche Verlagshandlung, 1871, Seite 15
- ↑Carl Spitz:Erster Cursus der Differential- und Integralrechnung.C. F. Winter’sche Verlagshandlung, 1871, Seite 16
- ↑T. Arens et al.:Mathematik.Spektrum, S. 422.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 170.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 292.
- ↑Serge Lang:A First Course in Calculus.Fifth Edition. Springer, S. 463–464.
- ↑John Stillwell:Mathematics and Its History,Third Edition, Springer, S. 192–194.
- ↑Serge Lang:Calculus of Several Variables,Third Edition, Springer, S. 439.
- ↑Serge Lang:Calculus of Several Variables,Third Edition, Springer, S. 434.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 161.
- ↑Serge Lang:Calculus of Several Variables,Third Edition, Springer, S. 435–436.
- ↑Hans Wußing,Heinz-Wilhelm Alten,Heiko Wesemüller-Kock,Eberhard Zeidler:6000 Jahre Mathematik: Von den Anfängen bis Newton und Leibniz.Springer, 2008, S. 429.
- ↑Thomas Sonar:3000 Jahre Analysis,Springer, S. 247–248.
- ↑Thomas Sonar:3000 Jahre Analysis,Springer, S. 378.
- ↑Marquis de L’Hospital:Analyse des Infiniment Petits pour l’Intelligence des Lignes Courbes.Preface, S. ix–x: « L’Étendue de ce calcul est immense:… »;archive.org.
- ↑Ernst Hairer,Gerhard Wanner:Analysis in historischer Entwicklung.Springer, S. 87.
- ↑John Stillwell:Mathematics and its history,Third Edition, Springer, S. 157.
- ↑Thomas Sonar:3000 Jahre Analysis,Springer, S. 424–425.
- ↑Hans Wußing, Heinz-Wilhelm Alten, Heiko Wesemüller-Kock, Eberhard Zeidler:6000 Jahre Mathematik: Von Euler bis zur Gegenwart.Springer, 2008, S. 233.
- ↑Thomas Sonar:3000 Jahre Analysis,Springer, S. 506–514.
- ↑Ernst Hairer, Gerhard Wanner:Analysis in historischer Entwicklung,Springer, S. 91.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 284.
- ↑Bronsteinet al.:Taschenbuch der Mathematik,Verlag Harri Deutsch, S. 394.
- ↑abcHerbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 318.
- ↑Jeremy Gray:The Real and the Complex: A History of Analysis in the 19th Century,Springer, S. 271–272.
- ↑Herbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 323.
- ↑abHerbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 324.
- ↑Differentialrechnung.In: Guido Walz (Hrsg.):Lexikon der Mathematik.1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000,ISBN 3-8274-0439-8.
- ↑Ernst Hairer, Gerhard Wanner:Analysis in historischer Entwicklung,Springer, S. 90.
- ↑Harro Heuser:Lehrbuch der Analysis.Teubner, Wiesbaden 2003,ISBN 3-519-62233-5,S. 269.
- ↑Thomas Sonar:3000 Jahre Analysis,Springer, S. 408.
- ↑Lokenath Debnath:The Legacy of Leonhard Euler – A Tricentennial Tribute,Imperial College Press, S. 26.
- ↑Ali Mason:Advanced Differential Equations.EDTECH, 1019,ISBN 1-83947-389-4,S.67.
- ↑Karl Bosch:Mathematik für Wirtschaftswissenschaftler.14. Auflage, Oldenbourg, 2003, S. 77
- ↑Klaus Hefft:Mathematischer Vorkurs zum Studium der Physik.2. Auflage. Springer, 2018, S. 97.
- ↑Herbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 329.
- ↑Herbert Amann, Joachim Escher:Analysis 1.3. Auflage. S. 358.
- ↑Herbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 330–331.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 304.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 32–33.
- ↑Ernst Hairer, Gerhard Wanner:Analysis in historischer Entwicklung,Springer, S. 248.
- ↑Herbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 335.
- ↑Herbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 336.
- ↑Herbert Amann, Joachim Escher:Analysis 1.3. Auflage. Birkhäuser, S. 346.
- ↑Terence Tao:Analysis II,Third Edition, Hindustan Book Agency, S. 64.
- ↑Terence Tao:Analysis II,Third Edition, Hindustan Book Agency, S. 65.
- ↑Jeremy Gray:The Real and the Complex: A History of Analysis in the 19th Century,Springer, S. 201.
- ↑Eberhard Freitag,Rolf Busam:Funktionentheorie 1,4. Auflage, Springer, S. 89.
- ↑Eberhard Freitag, Rolf Busam:Funktionentheorie 1,4. Auflage, Springer, S. 16 ff.
- ↑Eberhard Freitag, Rolf Busam:Funktionentheorie 1,4. Auflage, Springer, S. 35.
- ↑Eberhard Freitag, Rolf Busam:Funktionentheorie 1,4. Auflage, Springer, S. 42–43.
- ↑Eberhard Freitag, Rolf Busam:Funktionentheorie 1,4. Auflage, Springer, S. 45.
- ↑abHerbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 157.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 158.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 159.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 165.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 154–157.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 158–163.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 173.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 175.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 177.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 192.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 230–232.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 176.
- ↑Herbert Amann, Joachim Escher:Analysis 2.2. Auflage. Birkhäuser, S. 188.
- ↑abT. Arens et al.:Mathematik.Spektrum, S. 794.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 803.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 811.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 812.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 1193–1195.
- ↑T. Arens et al.:Mathematik.Spektrum, S. 1196.







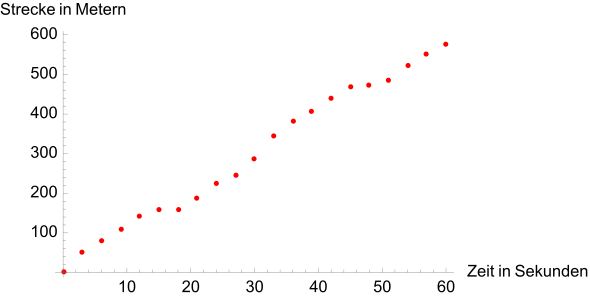
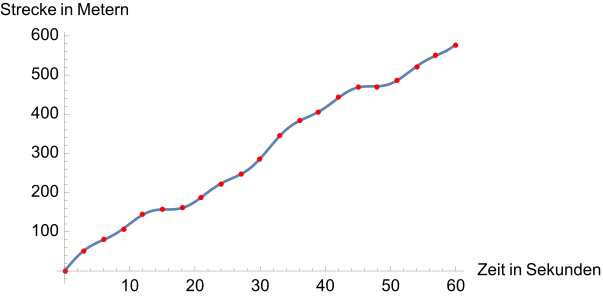

















































































































































![{\displaystyle [x_{0},x_{0}+\Delta x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c9fca7d2a7b17975192095def858d129b413b9)



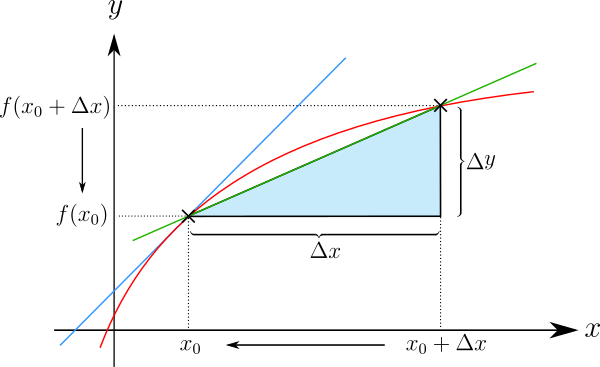










































































































![{\displaystyle f(x)={\sqrt[{m}]{x}}=x^{\frac {1}{m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6cb473bb3eb4fc3708532fd9ecc490e04a2f264)

![{\displaystyle f'(x)={\frac {1}{m}}{\frac {f}{x}}={\frac {1}{m}}\;{\frac {\sqrt[{m}]{x}}{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17d3630d048bade9d78586f3079b59cdea97b1ea)














































































![{\displaystyle u[v(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecd0b3af2d9804a34ab0fd2dad5a66481163343d)






































































![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
























![{\displaystyle f_{n}\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b32ac944f464748dfb697057d3788497bfabb6fe)
![{\displaystyle f_{n}'\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa20a73b34f9d8b5ab0dd50731c0f34dcabbb59f)
![{\displaystyle g\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/38132af5ea7cd916293fe93f29187bd461a5e270)

![{\displaystyle x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145)


![{\displaystyle ||f_{n}'||_{\infty }:=\sup _{x\in [a,b]}|f_{n}'(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c15371c13ae76eca92cdd6495b526d331581d44c)



![{\displaystyle f\colon [a,b]\times [c,d]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d985fd7a6c6afcc39f2bfa732015f9c55ebf223)


























































































































