Eulersche Zahl

DieEulersche Zahl,mit dem Symbol$e$bezeichnet, ist eineKonstante,die in der gesamtenAnalysisund allen damit verbundenenTeilgebieten der Mathematik,besonders in derDifferential-undIntegralrechnung,aber auch in derStochastik(Kombinatorik,Normalverteilung) eine zentrale Rolle spielt. Ihr numerischer Wert beträgt

$e=2{,}71828\,18284\,59045\,23536\,02874\,71352\,66249\,77572\,47093\,69995\,\dots$

$e$ist einetranszendenteund somit auchirrationalereelle Zahl.Sie ist dieBasisdes natürlichenLogarithmusund der (natürlichen)Exponentialfunktion.In derangewandten Mathematikspielt die Exponentialfunktion und somit$e$eine bedeutende Rolle bei der Beschreibung von Vorgängen wie demradioaktiven Zerfallund demnatürlichen Wachstum.

Es gibt zahlreiche äquivalente Definitionen von$e$,die bekannteste lautet:

$e=1+{\frac {1}{1}}+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}+{\frac {1}{1\cdot 2\cdot 3\cdot 4}}+\dotsb =\sum _{k=0}^{\infty }{\frac {1}{k!}}$

Die Zahl wurde nach dem SchweizerMathematikerLeonhard Eulerbenannt,der zahlreiche Eigenschaften von$e$beschrieb. Gelegentlich wird sie auch nach dem schottischen MathematikerJohn NapieralsNapiers Konstante(oderNepersche Konstante) bezeichnet. Sie gehört zu den wichtigsten Konstanten der Mathematik.

Es gibt einen internationalen Tag der eulerschen Zahl$e$.In Ländern, in denen wie in Deutschland beim Datum der Tag vor dem Monat (27.1.) geschrieben wird, ist er am 27. Januar,in Ländern, in denen wie in den USA der Monat vor dem Tag geschrieben wird (2/7), am 7. Februar.

Definition

Die Zahl$e$wurde von Leonhard Euler durch die folgendeReihedefiniert:

${\begin{aligned}e&=1+{\frac {1}{1}}+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}+{\frac {1}{1\cdot 2\cdot 3\cdot 4}}+\dotsb \\&={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+\dotsb \\&=\sum _{k=0}^{\infty }{\frac {1}{k!}}\\\end{aligned}}$

Für$k\in \mathbb {N} _{0}$ist dabei$k!$dieFakultätvon$k$,also im Falle$k>0$das Produkt$k!=1\cdot 2\cdot \ldots \cdot k$dernatürlichen Zahlenvon$1$bis$k$,während$0!:=1$definiert ist.

Wie schon Euler bewies, erhält man die Eulersche Zahl$e$auch alsfunktionalen Grenzwert.

Die Zahl$e$kann auch alsGrenzwertderFolge$(a_{n})_{n\in \mathbb {N} }$mit$a_{n}:=\left(1+{\frac {1}{n}}\right)^{n}$geschrieben werden:

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

Dem liegt zugrunde, dass

$e=\exp(1)=e^{1}$

gilt,$e$also derFunktionswertder Exponentialfunktion (oder auch „$e$-Funktion “) an der Stelle$1$ist. Die obige Reihendarstellung von$e$ergibt sich in diesem Zusammenhang dadurch, dass man dieTaylorreihe der Exponentialfunktionum die Entwicklungsstelle$0$an der Stelle$1$auswertet.

Ein alternativer Zugang zur Definition der Eulerschen Zahl ist derjenige überIntervallschachtelungen,etwa in der Weise, wie es inTheorie und Anwendung der unendlichen ReihenvonKonrad Knoppdargestellt wird. Danach gilt für alle$n\in \mathbb {N}$:

$\left(1+{\frac {1}{n}}\right)^{n}<e<\left(1+{\frac {1}{n}}\right)^{n+1}$

Grafische Hinführung zur Eulerschen Zahl$e$

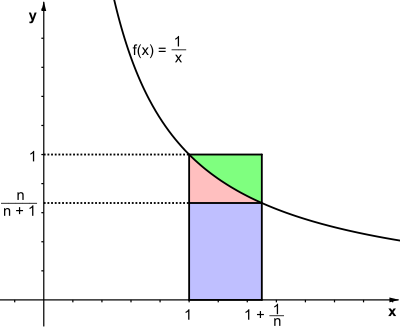
Die Entstehung der Zahl$e$lässt sich auch grafisch veranschaulichen. Aus der Abbildung ergibt sich folgender Zusammenhang:

${\frac {1}{n}}\cdot {\frac {n}{n+1}}\leq \int _{1}^{1+{\frac {1}{n}}}{\frac {1}{x}}\,\mathrm {d} x\leq {\frac {1}{n}}\cdot 1$

$\Leftrightarrow {\frac {1}{n}}\cdot {\frac {n}{n+1}}\leq \ln \left(1+{\frac {1}{n}}\right)\leq {\frac {1}{n}}\cdot 1$(Lösung des Integrals)

$\Leftrightarrow {\frac {n}{n+1}}\leq n\cdot \ln \left(1+{\frac {1}{n}}\right)\leq 1$(Multiplikation mit n)

$\Leftrightarrow {\frac {n}{n+1}}\leq \ln \left(1+{\frac {1}{n}}\right)^{n}\leq 1$(Anwendung eines Logarithmengesetzes)

$\Leftrightarrow \lim _{n\to \infty }{\frac {n}{n+1}}\leq \lim _{n\to \infty }\left(\ln \left(1+{\frac {1}{n}}\right)^{n}\right)\leq 1$(Grenzwertbildung)

$\Leftrightarrow \ln \left(\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right)=1$(Stetigkeit der Logarithmus-Funktion)

$\Leftrightarrow e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$(Umkehrfunktion der Exponentialfunktion)

Die Vorgeschichte vor Euler

Die Geschichte der Eulerschen Zahl$e$beginnt bereits im 16. Jahrhundert mit drei Problembereichen, in denen eine Zahl auftaucht, der sich damals die Mathematiker näherten und die später$e$genannt wurde:

• Als Basis von Logarithmen in denLogarithmentafelnvonJohn NapierundJost Bürgi.Beide hatten ihre Tafeln unabhängig voneinander entwickelt, wobei sie eine Idee vonMichael Stifelaufnahmen und Ergebnisse von Stifel und anderen Mathematikern des 16. Jahrhunderts benutzten. Bürgi veröffentlichte 1620 seine „Arithmetische und geometrische Progreß-Tabulen “. Als Basis seines Logarithmensystems verwendet Bürgi offenbar instinktiv eine Zahl, die nahe bei$e$liegt. Napier veröffentlichte 1614 seine „Mirifici logarithmorum canonis descriptio “und benutzt dabei eine zu$1/e$proportionale Basis.Napier und Bürgi wollten mit Hilfe der Logarithmentafeln Multiplikationen auf Additionen zurückführen, um so umfangreiche Rechnungen einfacher und weniger zeitaufwändig zu gestalten.
• Als Grenzwert einer Folge in der Zinseszinsrechnung. 1669 stellteJacob Bernoullidie Aufgabe: „Eine Summe Geldes sei auf Zinsen angelegt, dass in den einzelnen Augenblicken ein proportionaler Teil der Jahreszinsen zum Kapital geschlagen wird. “Diesen proportionalen Zinszuschlag nennen wir heute „stetige Verzinsung “.Bernoulli fragt, ob durch Verträge, bei denen die einzelnen Augenblicke immer kürzer werden, beliebig große Vielfache der Ausgangssumme erzielt werden können, und erreicht als Lösung eine Zahl, die wir heute als Eulersche Zahl$e$kennen.
• Als unendliche Reihe (Fläche der Hyperbel desApollonios von Perge). Es ging (in heutiger Sprache) umdie Frage,wie weit sich eine Fläche unter der Hyperbel$xy=1$von$x=1$nach rechts erstreckt, die genauso groß wie die Fläche des Einheitsquadrats ist. Der flämische MathematikerGrégoire de Saint-Vincent(latinisiert Gregorius a Sancto Vincentino) entwickelte zur Lösung eine Funktion, die wir heutenatürlichen Logarithmusnennen und mit$\ln$bezeichnen. Er entdeckte interessante Eigenschaften, darunter eine Gleichung, die wir heuteFunktionalgleichungdes Logarithmus nennen, die auch Napier und Bürgi zur Konstruktion und bei der Benutzung ihrer Logarithmentafeln benutzten.Es ist nicht gesichert, ob ihm bewusst war, dass die Basis dieses Logarithmus die Zahl ist, die später$e$genannt wurde. Aufgefallen ist dies erst nach Erscheinen seines Werkes.Spätestens sein Schüler und Co-AutorAlphonse Antonio de Sarasastellte den Zusammenhang durch eine Logarithmusfunktion dar. In einem Aufsatz, der die Verbreitung der Ideen von Saint-Vincent durch de Sarasa behandelt, heißt es, dass „die Beziehung zwischen Logarithmen und der Hyperbel in allen Eigenschaften durch Saint-Vincent gefunden wurde, nur nicht im Namen “.Durch Arbeiten vonNewtonundEulerwurde dann klar, dass$e$die Basis ist.Leibniz war offensichtlich der Erste, der einen Buchstaben für diese Zahl benutzte. In seiner Korrespondenz mitChristiaan Huygensvon 1690/1 benutzte er den Buchstaben b als Basis einer Potenz.

Herkunft des Symbolse

Als frühestes Dokument, das die Verwendung des Buchstabens$e$für diese Zahl durch Leonhard Euler aufweist, gilt ein Brief Eulers anChristian Goldbachvom 25. November 1731.Noch früher, 1727 oder 1728, begann Euler, den Buchstaben$e$zu benutzen, und zwar im Artikel „Meditatio in experimenta explosione tormentorum nuper instituta “über Explosivkräfte in Kanonen, der allerdings erst 1862 veröffentlicht wurde.Als nächste gesicherte Quelle für die Verwendung dieses Buchstabens gilt Eulers WerkMechanica sive motus scientia analytice exposita, IIaus dem Jahre 1736.In der im Jahre 1748 erschienenenIntroductio in analysin infinitorumgreift Euler diese Bezeichnung wieder auf.

Es gibt keine Hinweise darauf, dass diese Wahl des Buchstabens$e$in Anlehnung an seinen Namen geschah. Unklar ist auch, ob er dies in Anlehnung an die Exponentialfunktion oder aus praktischen Erwägungen der Abgrenzung zu den viel benutzten Buchstabena, b, coderdmachte. Obwohl auch andere Bezeichnungen in Gebrauch waren, etwacind’AlembertsHistoire de l’Académie,hat sich$e$durchgesetzt.

Im Formelsatz wird$e$nachDIN 1338und ISO 80000-2 nicht kursiv gesetzt, um die Zahl von einer Variablen zu unterscheiden.Allerdings ist auch die kursive Schreibweise verbreitet.

Eigenschaften

Die Eulersche Zahl$e$ist einetranszendente(BeweisnachCharles Hermite,1873) und damitirrationaleZahl (Beweis mit Kettenbrüchen für$e^{2}$und somit$e$bereits 1737 von Euler,Beweis imBeweisarchivbzw.Artikel). Sie lässt sich also (wie auch dieKreiszahl$\pi$nachFerdinand von Lindemann1882) nicht als Bruch zweiernatürlicher Zahlen(sogar nicht einmal als Lösung eineralgebraischen Gleichung) darstellen und besitzt folglich eine unendlichenichtperiodischeDezimalbruchentwicklung.DasIrrationalitätsmaßvon$e$ist 2 und somit so klein wie möglich für eine irrationale Zahl, insbesondere ist$e$nichtliouvillesch.Es ist nicht bekannt, ob$e$zu irgendeiner Basisnormalist.

In derEulerschen Identität

$e^{\mathrm {i} \cdot \pi }=-1$

werden fundamentale mathematische Konstanten in Zusammenhang gesetzt: dieganze Zahl1, die Eulersche Zahl$e$,dieimaginäre Einheit$\mathrm {i}$derkomplexen Zahlenund dieKreiszahl$\pi$.

Die Eulersche Zahl tritt auch in derasymptotischen Abschätzungder Fakultät auf (sieheStirlingformel):

${\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\leq n!\leq {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\cdot e^{\frac {1}{12n}}$

DieCauchy-Produktformelfür die beiden (jeweils absolut konvergenten) Reihen und derbinomische Lehrsatzergeben

$\sum _{k=0}^{\infty }{\frac {1}{k!}}\cdot \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}=\sum _{k=0}^{\infty }\sum _{j=0}^{k}{\frac {1}{j!}}{\frac {(-1)^{k-j}}{(k-j)!}}=\sum _{k=0}^{\infty }{\frac {1}{k!}}\sum _{j=0}^{k}{\binom {k}{j}}1^{j}(-1)^{k-j}=\sum _{k=0}^{\infty }(1+(-1))^{k}=\sum _{k=0}^{\infty }0^{k}=1=e\cdot e^{-1}$

und daraus folgt sofort:

$e^{-1}={\frac {1}{e}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}$

Geometrische Interpretation

Eine geometrische Interpretation der Eulerschen Zahl liefert dieIntegralrechnung.Danach ist$e$diejenige eindeutig bestimmte Zahl$b>1$,für die derInhalt der Flächeunterhalb desFunktionsgraphender reellenKehrwertfunktion$y={\tfrac {1}{x}}$imIntervall$[1,b]$exakt gleich$1$ist:

$\int _{1}^{e}{\frac {1}{x}}\,\mathrm {d} x=1$

Weitere Darstellungen für die Eulersche Zahl

Die Eulersche Zahl lässt sich auch durch

$e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}$

oder durch den Grenzwert des Quotienten ausFakultätundSubfakultätbeschreiben:

$e=\lim _{n\to \infty }{\frac {n!}{!n}}.$

Eine Verbindung zur Verteilung derPrimzahlenwird über die Formeln

$e=\lim _{n\to \infty }({\sqrt[{n}]{n}})^{\pi (n)}$

$e=\lim _{n\to \infty }{\sqrt[{n}]{n\#}}$

deutlich, wobei$\pi (n)$diePrimzahlfunktionund das Symbol$n\#$dasPrimorialder Zahl$n$bedeutet.

Auch eher von exotischem Reiz als von praktischer Bedeutung ist diecatalansche Darstellung

$e={\sqrt[{1}]{\frac {2}{1}}}\cdot {\sqrt[{2}]{\frac {4}{3}}}\cdot {\sqrt[{4}]{\frac {6\cdot 8}{5\cdot 7}}}\cdot {\sqrt[{8}]{\frac {10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}}\cdots$

Kettenbruchentwicklungen

Im Zusammenhang mit der Zahl$e$gibt es spätestens seit dem Erscheinen vonLeonhard EulersIntroductio in Analysin Infinitorumim Jahre 1748 eine große AnzahlKettenbruchentwicklungenfür$e$und aus$e$ableitbare Größen.

So hat Euler die folgende klassischeIdentitätfür$e$gefunden:

$(1){\begin{aligned}e&=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,\dotsc ]\\&=2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{4+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{6+\dotsb }}}}}}}}}}}}}}}}\end{aligned}}$(FolgeA003417inOEIS)

Die Identität (1) weist offenbar ein regelmäßiges Muster auf, das sich bis ins Unendliche fortsetzt. Sie gibt einenregulären Kettenbruchwieder, der von Euler aus dem folgenden abgeleitet wurde:

$(2){\begin{aligned}{\frac {e+1}{e-1}}&=[2;6,10,14,\dotsc ]\\&={2+{\cfrac {1}{6+{\cfrac {1}{10+{\cfrac {1}{14+{\cfrac {1}{\;\,\ddots }}}}}}}}}\\&\approx 2{,}1639534137386\end{aligned}}$(FolgeA016825inOEIS)

Dieser Kettenbruch ist seinerseits ein Spezialfall des folgenden mit$k=2$:

$(3){\begin{aligned}{\coth {\frac {1}{k}}}&={\frac {e^{\frac {2}{k}}+1}{e^{\frac {2}{k}}-1}}\\&=[k;3k,5k,7k,\dots ]\\&={k+{\cfrac {1}{3k+{\cfrac {1}{5k+{\cfrac {1}{7k+{\cfrac {1}{\;\,\ddots }}}}}}}}}\\\end{aligned}}$$(k=1,2,3,\dots )$

Eine andere klassische Kettenbruchentwicklung, die jedochnicht regelmäßigist, stammt ebenfalls von Euler:

$(4){\begin{aligned}{\frac {1}{e-1}}&={0+{\cfrac {1}{1+{\cfrac {2}{2+{\cfrac {3}{3+{\cfrac {4}{\;\,\ddots }}}}}}}}}\approx 0{,}58197670686932\end{aligned}}$(FolgeA073333inOEIS)

Auf Euler undErnesto Cesàrogeht eine weitere Kettenbruchentwicklung derEulerschen Zahlzurück, die von anderem Muster als in (1) ist:

$(5){\begin{aligned}e&=2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {2}{3+{\cfrac {3}{4+{\cfrac {4}{5+{\cfrac {5}{6+{\cfrac {6}{7+{\cfrac {7}{8+\dotsb }}}}}}}}}}}}}}}}\end{aligned}}$

Im Zusammenhang mit derEulerschen Zahlexistiert darüber hinaus eine große Anzahl von allgemeinen kettenbruchtheoretischenFunktionalgleichungen.So nenntOskar Perronals eine von mehreren die folgende allgemeingültige Darstellung der$e$-Funktion:

$(6){\begin{aligned}{e^{z}}&=1+{\cfrac {z}{1-{\cfrac {1z}{2+z-{\cfrac {2z}{3+z-{\cfrac {3z}{4+z-{\cfrac {4z}{5+z-{\cfrac {5z}{6+z-{\cfrac {6z}{7+z-{\cfrac {7z}{8+z-\dotsb }}}}}}}}}}}}}}}}\end{aligned}}$$(z\in \mathbb {C} )$

Ein weiteres Beispiel hierfür ist die vonJohann Heinrich Lambertstammende Entwicklung desTangens hyperbolicus,die zu denlambertschen Kettenbrüchengerechnet wird:

$(7){\begin{aligned}{\tanh z}&={\frac {e^{z}-e^{-z}}{e^{z}+e^{-z}}}\\&={\frac {e^{2z}-1}{e^{2z}+1}}\\&=0+{\cfrac {z}{1+{\cfrac {z^{2}}{3+{\cfrac {z^{2}}{5+{\cfrac {z^{2}}{7+{\cfrac {z^{2}}{9+{\cfrac {z^{2}}{11+{\cfrac {z^{2}}{13+{\cfrac {z^{2}}{15+\dotsb }}}}}}}}}}}}}}}}\end{aligned}}$$\left(z\in \mathbb {C} \setminus \left\{{\frac {\mathrm {i} \pi }{2}}+k\pi \colon k=0,1,2,3,\dotsc \right\}\right)$

Erst 2019 wurde mit Hilfe eines Computerprogrammes, das nachSrinivasa RamanujanalsRamanujan-Maschinebenannt wurde, letztlich basierend auf einerTrial-and-error-Methode,durch ein Team um Gal Raayoni amTechnioneine weitere und bisher unbekannte Kettenbruchentwicklung für die Eulersche Zahl gefunden. Gegenüber allen bisher bekannten Kettenbruchentwicklungen, die alle von einer beliebigen ganzzahligen Zahl, die kleiner als die Eulersche Zahl ist, aufsteigen, handelt es sich hier erstmals um eine, die von der ganzen Zahl3,einer ganzen Zahl, die größer ist als die Eulersche Zahl, absteigt.Allein die Auffindung eines (einzigen) solchen absteigenden Kettenbruchs von einer ganzen Zahl größer als die Eulersche Zahl$(3>e)$legt die Vermutung nahe, dass es unendlich viele solcher absteigenden Kettenbrüche von ganzen Zahlen$n$mit$n>e$gibt, die ebenfalls auf die Eulersche Zahl führen.

$(8){\begin{aligned}e&=3+{\cfrac {-1}{4+{\cfrac {-2}{5+{\cfrac {-3}{6+{\cfrac {-4}{7+{\cfrac {-5}{8+\dotsb }}}}}}}}}}\end{aligned}}$

Anschauliche Interpretationen der Eulerschen Zahl

Zinseszinsrechnung

Das folgende Beispiel macht die Berechnung der Eulerschen Zahl nicht nur anschaulicher, sondern es beschreibt auch die Geschichte der Entdeckung der Eulerschen Zahl: Ihre ersten Stellen wurden vonJakob I Bernoullibei der Untersuchung der Zinseszinsrechnung gefunden.

Den Grenzwert der ersten Formel kann man folgendermaßen deuten: Jemand zahlt am 1. Januar einenEuroauf der Bank ein. DieBankgarantiert ihm eine momentaneVerzinsungzu einemZinssatz$z=100\,\%$pro Jahr. Wie groß ist sein Guthaben am 1. Januar des nächsten Jahres, wenn er die Zinsen zu gleichen Bedingungen anlegt?

Nach derZinseszinsformelwird aus dem Startkapital$K_{0}$nach$n$Verzinsungen mit Zinssatz$z$das Kapital

$K_{n}=K_{0}(1+z)^{n}.$

In diesem Beispiel sind$K_{0}=1$und$z=100\,\%=1$,wenn der Zinszuschlag jährlich erfolgt, oder$z=1/n$,wenn der Zinszuschlag$n$-mal im Jahr erfolgt, also beiunterjähriger Verzinsung.

Bei jährlichem Zuschlag wäre

$K_{1}=1\cdot (1+1)^{1}=2{,}00.$

Bei halbjährlichem Zuschlag hat man$z={\frac {1}{2}}$,

$K_{2}=1\cdot \left(1+{\frac {1}{2}}\right)^{2}=2{,}25$

also schon etwas mehr. Bei täglicher Verzinsung$(z=1/365)$erhält man

$K_{365}=1\cdot \left(1+{\frac {1}{365}}\right)^{365}=2{,}714567.$

Wenn die Verzinsung kontinuierlich in jedem Augenblick erfolgt, wird$n$unendlich groß, und man bekommt die oben angegebene erste Formel für$e$.

Wahrscheinlichkeitsrechnung

$e$ist auch häufig in derWahrscheinlichkeitstheorieanzutreffen: Beispielsweise sei angenommen, dass ein Bäcker für jedes Brötchen eine Rosine in den Teig gibt und diesen gut durchknetet. Danach enthält statistisch gesehen jedes$e$-te Brötchen keine Rosine. DieWahrscheinlichkeit$p$,dass bei$n$Brötchen keine der$n$Rosinen in einem fest gewählten ist, ergibt im Grenzwert für$n\to \infty$(37-%-Regel):

$p=\lim _{n\to \infty }\left({\frac {n-1}{n}}\right)^{n}=\lim _{n\to \infty }\left(1-{\frac {1}{n}}\right)^{n}={\frac {1}{e}}.$

Es werden Briefe und die zugehörigen Briefumschläge mit den Adressen unabhängig voneinander geschrieben. Dann werden ohne hinzusehen, also rein zufällig, die Briefe in die Briefumschläge gesteckt. Wie groß ist die Wahrscheinlichkeit, dass kein Brief im richtigen Umschlag steckt? Euler löste diese Aufgabe und veröffentlichte sie 1751 im Aufsatz „Calcul de la probabilité dans le jeu de rencontre “. Bemerkenswert ist, dass sich ab einer Anzahl von sieben Briefen die Wahrscheinlichkeit fast nicht mehr ändert. Sie wird sehr gut durch$1/e=0{,}367879\dots \approx 36{,}7879\,\%$angenähert, denGrenzwertder Wahrscheinlichkeiten, wenn die Anzahl an Briefen immer größer wird.

Einem Jäger steht nur ein Schuss zur Verfügung. Er soll aus einer Schar Tauben, deren Anzahl$n$er kennt, die in zufälliger Reihenfolge an ihm vorbeifliegen, die größte schießen. Mit welcher Strategie sind seine Chancen maximal, die größte Taube zu treffen? Dieses Taubenproblem wurde vom amerikanischen MathematikerHerbert Robbinsformuliert. Dasselbe Entscheidungsproblem besteht auch bei der Anstellung des besten Mitarbeiters bei$n$Bewerbern (Sekretärinnenproblem) und ähnlichen Einkleidungen. Lösung: Die optimale Strategie besteht darin, erst$k$Tauben$(k<n)$vorbeifliegen zu lassen und dann auf die nächste Taube zu schießen, die größer als alle bisher vorbeigeflogenen ist, oder auf die allerletzte, wenn bis dahin keine größere vorbeigeflogen ist. Die Wahrscheinlichkeit, die größte Taube zu erwischen, beträgt bei dieser optimalen Strategie ungefähr$1/e$unabhängig von$n$,das jedoch nicht zu klein sein sollte. Wenn wir$k/n$als Schätzwert für$1/e$wählen, dann folgt$k\approx 1/e\cdot n$.Also sollte man bei 27 Tauben erst 10 vorbeifliegen lassen. Bemerkenswert ist, dass man bei rund$2/3$aller Fälle nicht die gewünschte optimale Lösung erhält.

Bei derPoisson-,derExponential-und derNormalverteilungwird$e$neben anderen Größen zur Beschreibung der Verteilung benutzt.

Bedeutung in der Mathematik

Die Eulersche Zahl taucht an verschiedenen wichtigen Stellen in der Mathematik auf:

• Sie dient zurDefinition$f(x\mid \mu,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\operatorname {exp} \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$derNormalverteilung,einerWahrscheinlichkeitsverteilung.
• Sie dient zurDefinition$P_{\lambda }(k)={\frac {\lambda ^{k}}{k!}}\,e^{-\lambda }$derPoisson-Verteilung,einerWahrscheinlichkeitsverteilung.
• Sie ist in derStirling-Formel$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}$für dieFakultätenthalten.
• Sie ist in derDefinition$\Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}\mathrm {d} t$derGammafunktionenthalten.
• Sie ist in der Formel${!}n=\left\lfloor {\frac {n!+1}{e}}\right\rfloor$für dieSubfakultätenthalten.

DieExponentialfunktionzur Basis der Eulerschen Zahl lautet:

$f(x)=e^{x}$

DieAbleitungsfunktionlautet:

$f'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}$

Daraus folgt, dass diese Exponentialfunktion mit ihrer Ableitungsfunktion identisch ist:

$f(x)=f'(x)$

Dies bedeutet anschaulich, dass die Steigung dieser Exponentialfunktion an jeder Stelle genauso groß ist wie der Funktionswert.

Auch in derDifferentialrechnungkommt die Eulersche Zahl vor. An der Stelle$e$liegt das Maximum der Funktion$f(x)=x^{\tfrac {1}{x}}=e^{\tfrac {\ln(x)}{x}}$.Außerdem befindet sich an der Stelle$e^{-1}$das Minimum der Funktion$f(x)=x^{x}=e^{x\cdot \ln(x)}$.Das kann jeweils mithilfe derAbleitungsfunktiongezeigt werden.

Charakterisierung der Eulerschen Zahl nach Steiner

Im vierzigsten Band vonCrelles Journalaus dem Jahre 1850 gibt der Schweizer MathematikerJakob Steinereine Charakterisierung derEulerschen Zahl$e$,wonach$e$als Lösung einerExtremwertaufgabeverstanden werden kann. Steiner zeigte nämlich, dass die Zahl$e$charakterisierbar ist als diejenige eindeutig bestimmtepositivereelle Zahl,die beimWurzelziehenmit sich selbst die größte Wurzel liefert. Wörtlich schreibt Steiner: „Wird jede Zahl durch sich selbst radicirt, so gewährt die Zahl e die allergrößte Wurzel. “

Steiner behandelt hier die Frage, ob für dieFunktion

$f\colon (0,\infty )\to (0,\infty ),\;x\mapsto f(x)={\sqrt[{x}]{x}}=x^{\frac {1}{x}}$

dasglobale Maximumexistiert und wie es zu bestimmen ist. Seine Aussage ist, dass es existiert und dass es angenommen wird in und nur in$x_{\mathrm {max} }=e$.

In seinem BuchTriumph der MathematikgibtHeinrich Dörrieeine elementare Lösung dieser Extremwertaufgabe. Sein Ansatz geht von der folgenden wahren Aussage über die reelleExponentialfunktionaus:

$\forall y\in \mathbb {R} \setminus \{0\}\colon e^{y}>1+y$

Nach der Substitution$y={\frac {x-e}{e}}$folgt für alle reellen Zahlen$x\neq e$

$e^{\frac {x-e}{e}}>1+{\frac {x-e}{e}},$

mittels einfacherUmformungenweiter

$e^{\frac {x}{e}}>x$

und schließlich für alle positiven$x\neq e$durch Radizieren

${\sqrt[{e}]{e}}>{\sqrt[{x}]{x}}.$

Bruchnäherungen

Für die Zahl$e$und daraus abgeleiteteGrößengibt es verschiedene näherungsweise Darstellungen mittelsBrüchen.So fandCharles Hermitedie folgenden Bruchnäherungen:

$e\approx {\frac {58291}{21444}}\approx 2{,}718289498$

$e^{2}\approx {\frac {158452}{21444}}\approx 7{,}38910651$

Hier weicht der erstgenannte Bruch um weniger als 0,0003 Prozent von$e$ab.

Die optimale Bruchnäherung im dreistelligen Zahlenbereich, also die optimale Bruchnäherung$e\approx {\frac {Z_{0}}{N_{0}}}$mit$N_{0},Z_{0}<1000$,ist

$e\approx {\frac {878}{323}}\approx 2{,}718266254$.

Diese Näherung ist jedoch nicht die beste Bruchnäherung im Sinne der Forderung, dass der Nenner höchstens dreistellig sein soll. Die in diesem Sinnebeste Bruchnäherungergibt sich als 9.Näherungsbruch der Kettenbruchentwicklungder Eulerschen Zahl:

$e\approx {\frac {1457}{536}}\approx 2{,}71828358\dots$

Aus den Näherungsbrüchen der zu$e$gehörenden Kettenbruchentwicklungen (s. o.) ergeben sich Bruchnäherungen beliebiger Genauigkeit für$e$und daraus abgeleitete Größen. Mit diesen findet man sehr effizientbeste Bruchnäherungender Eulerschen Zahl in beliebigen Zahlenbereichen. So erhält etwa im fünfstelligen Zahlenbereich die beste Bruchnäherung

$e\approx {\frac {49171}{18089}}\approx 2{,}718281828735\dots$,

die zeigt, dass die von Charles Hermite für die Eulersche Zahl im fünfstelligen Zahlenbereich gefundene Bruchnäherung noch nicht optimal war.

In gleicher Weise hat etwaC. D. Oldsgezeigt, dass durch die Näherung

${\frac {e-1}{2}}\approx {\frac {342762}{398959}}$

für die Eulersche Zahl eine weitere Verbesserung, nämlich

$e\approx {\frac {1084483}{398959}}\approx 2{,}7182818284585\dots$,

zu erzielen ist.

Insgesamt beginnt die Folge der besten Näherungsbrüche der Eulerschen Zahl, die sich aus ihrer regelmäßigen Kettenbruchdarstellung ergeben, folgendermaßen:

${\frac {p_{0}}{q_{0}}}=[2]={\frac {2}{1}}$

${\frac {p_{1}}{q_{1}}}=[2;1]={\frac {3}{1}}$

${\frac {p_{2}}{q_{2}}}=[2;1,2]={\frac {8}{3}}$

${\frac {p_{3}}{q_{3}}}=[2;1,2,1]={\frac {11}{4}}$

${\frac {p_{4}}{q_{4}}}=[2;1,2,1,1]={\frac {19}{7}}$

${\frac {p_{5}}{q_{5}}}=[2;1,2,1,1,4]={\frac {87}{32}}$

${\frac {p_{6}}{q_{6}}}=[2;1,2,1,1,4,1]={\frac {106}{39}}$

${\frac {p_{7}}{q_{7}}}=[2;1,2,1,1,4,1,1]={\frac {193}{71}}$

${\frac {p_{8}}{q_{8}}}=[2;1,2,1,1,4,1,1,6]={\frac {1264}{465}}$

${\frac {p_{9}}{q_{9}}}=[2;1,2,1,1,4,1,1,6,1]={\frac {1457}{536}}$

${\frac {p_{10}}{q_{10}}}=[2;1,2,1,1,4,1,1,6,1,1]={\frac {2721}{1001}}$

${\frac {p_{11}}{q_{11}}}=[2;1,2,1,1,4,1,1,6,1,1,8]={\frac {23225}{8544}}$

$\dots$

${\frac {p_{20}}{q_{20}}}=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,14]={\frac {410105312}{150869313}}$

$\dots$

Berechnung der Nachkommastellen

Zur Berechnung der Nachkommastellen wird meist die Reihendarstellung

$e=\sum _{k=0}^{\infty }{\frac {1}{k!}}={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+\dotsb =1+1+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+\dotsb$

ausgewertet, die schnell konvergiert. Wichtig bei der Implementierung ist dabeiLangzahlarithmetik,damit dieRundungsfehlernicht das Ergebnis verfälschen. Ein Verfahren, das ebenfalls auf dieser Formel beruht, aber ohne aufwendige Implementierung auskommt, ist derTröpfelalgorithmuszur Berechnung der Nachkommastellen von$e$,den A. H. J. Sale fand.

Entwicklung der Anzahl der bekannten Nachkommastellen von$e$

Datum	Anzahl	Mathematiker
1748	23	Leonhard Euler
1853	137	William Shanks
1871	205	William Shanks
1884	346	J. Marcus Boorman
1946	808	?
1949	2.010	John von Neumann(berechnet auf demENIAC)
1961	100.265	Daniel ShanksundJohn Wrench
1981	116.000	Steve Wozniak(berechnet mithilfe einesApple II)
1994	10.000.000	Robert Nemiroff und Jerry Bonnell
Mai 1997	18.199.978	Patrick Demichel
August 1997	20.000.000	Birger Seifert
September 1997	50.000.817	Patrick Demichel
Februar 1999	200.000.579	Sebastian Wedeniwski
Oktober 1999	869.894.101	Sebastian Wedeniwski
21. November 1999	1.250.000.000	Xavier Gourdon
10. Juli 2000	2.147.483.648	Shigeru Kondo und Xavier Gourdon
16. Juli 2000	3.221.225.472	Colin Martin und Xavier Gourdon
2. August 2000	6.442.450.944	Shigeru Kondo und Xavier Gourdon
16. August 2000	12.884.901.000	Shigeru Kondo und Xavier Gourdon
21. August 2003	25.100.000.000	Shigeru Kondo und Xavier Gourdon
18. September 2003	50.100.000.000	Shigeru Kondo und Xavier Gourdon
27. April 2007	100.000.000.000	Shigeru Kondo und Steve Pagliarulo
6. Mai 2009	200.000.000.000	Shigeru Kondo und Steve Pagliarulo
20. Februar 2010	500.000.000.000	Alexander Yee
5. Juli 2010	1.000.000.000.000	Shigeru Kondo
24. Juni 2015	1.400.000.000.000	Ellie Hebert
14. Februar 2016	1.500.000.000.000	Ron Watkins
29. Mai 2016	2.500.000.000.000	„yoyo “– unverifizierte Kalkulation
29. August 2016	5.000.000.000.000	Ron Watkins
3. Januar 2019	8.000.000.000.000	Gerald Hofmann
11. Juli 2020	12.000.000.000.000	David Christle
22. November 2020	31.415.926.535.897	David Christle

Die Eulersche Zahl in den Medien

In der FernsehserieDie Simpsonsund ihrer NachfolgeserieFuturamakommen viele mathematische Bezüge vor, einige haben auch mit der eulerschen Zahl$e$und Euler zu tun.

1995 gewährte in der FernsehserieAkte X – Die unheimlichen Fälle des FBIdie Zahlenreihe 2-7-1-8-2-8 zwei FBI-Agenten den Zutritt zu einem geheimen Archiv. Dort war nicht von der Eulerschen Zahl, sondern von Napiers Konstante die Rede.

Literatur

• Brian J. McCartin:e: The Master of All.Mathematical Intelligencer, Band 28, 2006, Nr. 2, S. 10–21. Der Artikel erhielt denChauvenet-Preis.mathdl.maa.org
• Heinrich Dörrie:Triumph der Mathematik. Hundert berühmte Probleme aus zwei Jahrtausenden mathematischer Kultur.5. Auflage. Physica-Verlag, Würzburg 1958.
• Leonhard Euler:Einleitung in die Analysis des Unendlichen.Erster Teil derIntroductio in Analysin Infinitorum.Springer Verlag, Berlin / Heidelberg / New York 1983,ISBN 3-540-12218-4(MR0715928– Reprint der Ausgabe Berlin 1885).
• Ernst Hairer,Gerhard Wanner:Analysis in historischer Entwicklung.Springer-Verlag, Berlin, Heidelberg 2011,ISBN 978-3-642-13766-2.
• Konrad Knopp:Theorie und Anwendung der unendlichen Reihen(=Die Grundlehren der Mathematischen Wissenschaften.Band2). 5., berichtigte Auflage. Springer Verlag, Berlin / Göttingen / Heidelberg / New York 1964,ISBN 3-540-03138-3(MR0183997).
• Eli Maor:e: the Story of a Number.Princeton University Press, Princeton 1994,ISBN 978-0-691-14134-3.
• Eli Maor:Die Zahl e: Geschichte und Geschichten.Birkhäuser Verlag, Basel (u. a.) 1996,ISBN 3-7643-5093-8.
• C. D. Olds:The simple continued fraction expansion of e.In:American Mathematical Monthly.Band77,1971,S.968–974.
• Oskar Perron:Irrationalzahlen.Nachdruck der 2., durchgesehenen Auflage (Berlin, 1939). 4. durchgesehene und ergänzte. Walter de Gruyter Verlag, Berlin 2011,ISBN 978-3-11-083604-2,doi:10.1515/9783110836042.fm.
• Oskar Perron:Die Lehre von den Kettenbrüchen – Band II: Analytisch-funktionentheoretische Kettenbrüche.Reprografischer Nachdruck der dritten, verbesserten und durchgesehenen Auflage, Stuttgart 1957. 4. durchgesehene und ergänzte. Teubner Verlag, Stuttgart 1977,ISBN 3-519-02022-X.
• J. Steiner:Über das größte Product der Theile oder Summanden jeder Zahl.In:Journal für die reine und angewandte Mathematik.Band40,1850,S.208(gdz.sub.uni-goettingen.de).
• David Wells:Das Lexikon der Zahlen. Aus dem Englischen von Dr. Klaus Volkert.Originaltitel: The Penguin Dictionary of Curious and Interesting Numbers. Fischer Taschenbuch Verlag, Frankfurt/Main 1990,ISBN 3-596-10135-2.

Weblinks

Commons:Eulersche Zahl– Sammlung von Bildern, Videos und Audiodateien

Wiktionary: eulersche Zahl– Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Eric W. Weisstein:e.In:MathWorld(englisch).
• Matheguru, Die Zahl e,Verständliche Erklärung und Herleitung der Eulerschen Zahl
• eauf eine Million Stellenbei Project Gutenberg (englisch)
• Xavier Gourdon, Pascal Sebah, The constant e and its computation,Ausführliche Informationen und Angaben zu relevanter Literatur (englisch)
• The number e, MacTutor History of Mathematics