Fourier-Transformation

DieFourier-Transformation(genauer diekontinuierliche Fourier-Transformation;Aussprache:[fuʁie]) ist eine mathematische Methode aus dem Bereich derFourier-Analyse,mit deraperiodischeSignale in ein kontinuierlichesSpektrumzerlegt werden. Die Funktion, die dieses Spektrum beschreibt, nennt man auchFourier-TransformierteoderSpektralfunktion.Es handelt sich dabei um eineIntegraltransformation,die nach dem MathematikerJean Baptiste Joseph Fourierbenannt ist. Fourier führte im Jahr 1822 dieFourier-Reiheein, die jedoch nur für periodische Signale definiert ist und zu einem diskreten Frequenzspektrum führt.

Es gibt einige Anwendungsfälle, in denen die Fourier-Transformation mittels eines Computers berechnet werden soll. Dafür wurde dieDiskrete Fourier-Transformationbeziehungsweise dieSchnelle Fourier-Transformationeingeführt.

Definition

Sei$f\in L^{1}(\mathbb {R} ^{n})$eine integrierbare Funktion, wobei$L^{1}$denLebesgue-Raumbezeichnet. Die (kontinuierliche) Fourier-Transformierte${\mathcal {F}}f$von$f$ist definiert durch

$({\mathcal {F}}f)(y)={\frac {1}{{\sqrt {2\pi }}^{\ n}}}\int _{\mathbb {R} ^{n}}f(x)\,\mathrm {e} ^{-\mathrm {i} y\cdot x}\,\mathrm {d} x$

und die zugehörige inverse Transformation lautet:

$f(x)={\frac {1}{{\sqrt {2\pi }}^{\ n}}}\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{\mathrm {i} y\cdot x}\,\mathrm {d} y\;.$

Dabei gilt:$\mathrm {d} x$und$\mathrm {d} y$sind$n$-dimensionaleVolumenelemente,$\mathrm {i}$dieimaginäre Einheitund$y\cdot x$dasStandardskalarproduktder Vektoren$y$und$x$.

Die Normierungskonstante ist in der Literatur nicht einheitlich. In der Theorie der Pseudodifferentialoperatoren und in der Signalverarbeitung ist es üblich, den Faktor$1/(2\pi )^{n/2}$in der Transformation wegzulassen, sodass stattdessen die Rücktransformation den Vorfaktor$1/(2\pi )^{n}$erhält. Die Transformation lautet dann:

$({\mathcal {F}}f)(y)=\int _{\mathbb {R} ^{n}}f(x)\,\mathrm {e} ^{-\mathrm {i} y\cdot x}\,\mathrm {d} x\;,$

$f(x)={\frac {1}{(2\pi )^{n}}}\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{\mathrm {i} y\cdot x}\,\mathrm {d} y\;.$

Hier taucht ein Vorfaktor auf, so dass die Anwendung desSatzes von Plancherelnicht direkt möglich ist, weil die Fouriertransformation dann keineunitäre Abbildungmehr auf$L^{1}(\mathbb {R} ^{n})\cap L^{2}(\mathbb {R} ^{n})$ist und so dieSignalleistungändert. Dies kann jedoch (wie bei allen Orthogonaltransformationen) einfach durch eine Substitution (Reskalierung der Abszisse) ausgeglichen werden und stellt damit kein grundlegendes Problem dar. Genau dies wird in der Literatur zu Signalverarbeitung und Systemtheorie vorgeschlagen, indem von der natürlichen Frequenz auf die Kreisfrequenz$\omega =2\pi y$(die den Faktor beinhaltet) übergegangen wird:

$({\mathcal {F}}f)(y)=\int _{\mathbb {R} ^{n}}f(x)\,\mathrm {e} ^{-2\pi \mathrm {i} y\cdot x}\,\mathrm {d} x\;=\int _{\mathbb {R} ^{n}}f(x)\,\mathrm {e} ^{-\mathrm {i} \omega \cdot x}\,\mathrm {d} x\;$

$f(x)=\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{2\pi \mathrm {i} y\cdot x}\,\mathrm {d} y\;=\int _{\mathbb {R} ^{n}}({\mathcal {F}}f)(y)\,\mathrm {e} ^{\mathrm {i} \omega \cdot x}\,\mathrm {d} y\;.$

Die reelle Form der Fourier-Transformation wird alsHartley-Transformationbezeichnet. Für reelle Funktionen$f$kann die Fourier-Transformation durch dieSinus- und Kosinus-Transformationsubstituiert werden.

Anwendungsfälle

Kompressionsverfahren für die digitale Kommunikation

Die Kompression von digitalen Daten auf Basis der Fourier-Transformation ist eine zentrale Technologie für Kommunikation, Datenaustausch undStreamingvon Medien im (mobilen) Internet.

Beispielsweise wird zur Kompression von Audio-Daten (etwa um eineMP3Datei zu erzeugen) das Audio-Signal in den Frequenz-Raum transformiert. Die Transformation erfolgt über das Verfahren der(modifizierten) diskreten Kosinustransformation,welches derschnellen Fourier-Transformationähnelt. Im Frequenzraum werden dann alle Frequenzen, die Menschen nicht hören können oder die nur wenig zum subjektiven Empfinden des Klangs beitragen, entfernt. Das Ergebnis wird im letzten Schritt aus dem Frequenz-Raumrücktransformiert– daraus erhält man, auf Grund des verringerten Frequenzumfangs, eine deutlich kleinere (komprimierte) Audio-Datei.

In vergleichbaren Verfahren können Bilder (JPEGKompression) oder Filme (MPEG-4) komprimiert werden.

Signalanalyse

In derSignalanalysewerden mittels Fourier-TransformationFrequenzanalysenvon Signalen durchgeführt. Hierzu wird das Verfahren derdiskreten Fourier-Transformationbzw. derschnellen Fourier-Transformationgenutzt. Ein Beispiel für dieVielzahl von technischen Anwendungenist die Nutzung der Signalanalyse bei der Erstellung von Bildern mittelsMagnetresonanztomographie.

Beispiel Signalanalyse in der Akustik

Der reineKammerton${\bar {a}}$ist eine Sinuswelle mit der Frequenz 440 Hz, also 440 Schwingungen pro Sekunde. Eine ideale Stimmgabel gibt genau dieses Sinussignal ab. Der gleiche Ton gespielt mit einem anderen Musikinstrument (nicht-ideale Stimmgabel), ist eine Zusammensetzung/Überlagerung aus Wellen verschiedener Wellenlängen. Diese sind bezüglich ihrer Frequenz normalerweise ganzzahlige Vielfache der Frequenz des Grundtons. Die Zusammensetzung und jeweilige Amplitude dieser Wellen ist bestimmend für dieKlangfarbejedes Musikinstruments. Nur die Welle mit der größten Wellenlänge, derGrundtondes Signals, hat dabei die Frequenz 440 Hz. Die anderen Wellen, dieObertöne,haben höhere Frequenzen.

An der Fourier-Transformierten des Tonsignals kann man direkt die verschiedenen Frequenzen/Wellenlängen der Wellenzusammensetzung ablesen. Diese Eigenschaft kann man beispielsweise für die automatische Erkennung von Tonhöhen und Musikinstrumenten in einem Tonsignal ausnutzen.

Beispiele

Bildliche Darstellung einer Funktion und ihrer Fourier-Transformierten

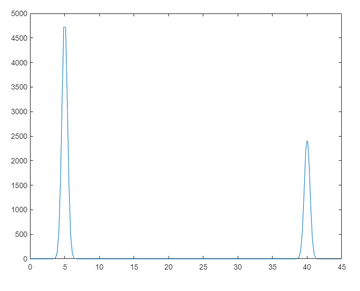
Zur Veranschaulichung sei ein Puls-Signal mit zwei überlagerten Frequenzen gegeben. Die Funktion, die dieses Signal darstellt, besteht beispielhaft aus der Summe zweier Cosinus-Funktionen, multipliziert mit einer Gauß-Kurve zur Darstellung des An- und Abklingens:

$f(t)=(10\cdot \cos(2\pi (5\cdot t))+(5\cdot \cos(2\pi (40\cdot t))))\cdot \mathrm {e} ^{-\pi t^{2}}$

Interpretiert man die Einheit der Zeitachsetals Sekunden, dann haben die beiden Frequenzen einen Wert von 5 Hz bzw. 40 Hz bei einer Amplitude von 10 bzw. 5.

Durch die Fourier-Transformation transformiert man die Funktion in den Frequenz-Raum – d. h., die X-Achse im Diagramm der Fourier-Transformierten stellt eine Frequenz dar. Die Fourier-Transformierte der Beispiel-Funktion zeigt die beiden Frequenz-Anteile als Spitze beim jeweiligen Frequenzwert (5 bzw. 40). Der Wert der Fourier-Transformierten an der Stelle der jeweiligen Frequenz ist ein Maß für die Amplitude der überlagerten Frequenzen in der Beispiel-Funktion. Hier dargestellt ist der absolute Betrag der Fourier-Transformierten bei normierter X-Achse (zur Vereinfachung ist nur der positive Teil der Transformierten gezeigt):

• 
  Funktion des Puls-Signalsf(t)
• 
  Positiver Teil des absoluten Betrags der Fourier-Transformierten

Dies illustriert die Anwendung der Fourier-Transformation zur Analyse der Frequenzanteile von Signalen – hieraus leitet sich auch das SynonymSpektralfunktionfür die Fourier-Transformierte ab.

Beispielhafte Berechnung einer Fourier-Transformierten

Es soll das Frequenzspektrum einer gedämpften Schwingung mit ausreichend schwacher Dämpfung untersucht werden. Diese kann durch folgende Funktion beschrieben werden:

$f(t)=x_{0}\cdot \mathrm {e} ^{-{\frac {t}{\tau }}}\cdot \cos(\omega _{\rm {s}}t)\Theta (t)$

oder in komplexer Schreibweise:

$f(t)=x_{0}\cdot \mathrm {e} ^{-{\frac {t}{\tau }}}\cdot {\tfrac {1}{2}}(\mathrm {e} ^{\mathrm {i} \omega _{\rm {s}}t}+\mathrm {e} ^{-\mathrm {i} \omega _{\rm {s}}t})\Theta (t)\;.$

Hier ist$x_{0}$dieAmplitudeund$\omega _{\rm {s}}$dieKreisfrequenzder Schwingung,$\tau$die Zeit, in der die Amplitude um den Faktor$1/e$abfällt, und$\Theta (t)$dieHeaviside-Funktion. Das heißt, die Funktion ist nur für positive Zeiten nicht null.

Man erhält

${\begin{aligned}F(\omega )=({\mathcal {F}}f)(\omega )&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(t)\mathrm {e} ^{-\mathrm {i} \omega t}\,\mathrm {d} t\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }x_{0}\cdot \mathrm {e} ^{-t/\tau }\cdot {\tfrac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} \omega _{\rm {s}}t}+\mathrm {e} ^{-\mathrm {i} \omega _{\rm {s}}t}\right)\Theta (t)\cdot \mathrm {e} ^{-\mathrm {i} \omega t}\,\mathrm {d} t\\&={\frac {x_{0}}{\sqrt {2\pi }}}\int _{0}^{\infty }\mathrm {e} ^{-t/\tau }\cdot {\tfrac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} \omega _{\rm {s}}t}+\mathrm {e} ^{-\mathrm {i} \omega _{\rm {s}}t}\right)\cdot \mathrm {e} ^{-\mathrm {i} \omega t}\,\mathrm {d} t\\&={\frac {x_{0}}{2{\sqrt {2\pi }}}}\int _{0}^{\infty }\left(\mathrm {e} ^{-t\left(1/\tau -\mathrm {i} (\omega _{\rm {s}}-\omega )\right)}+\mathrm {e} ^{-t\left(1/\tau +\mathrm {i} (\omega _{\rm {s}}+\omega )\right)}\right)\,\mathrm {d} t\\&={\frac {x_{0}}{2{\sqrt {2\pi }}}}\left[-{\frac {1}{1/\tau -\mathrm {i} (\omega _{\rm {s}}-\omega )}}\mathrm {e} ^{-t\left(1/\tau -\mathrm {i} (\omega _{\rm {s}}-\omega )\right)}-{\frac {1}{1/\tau +\mathrm {i} (\omega _{\rm {s}}+\omega )}}\mathrm {e} ^{-t\left(1/\tau +\mathrm {i} (\omega _{\rm {s}}+\omega )\right)}\right]_{0}^{\infty }\\&={\frac {x_{0}}{2{\sqrt {2\pi }}}}\left({\frac {1}{1/\tau -\mathrm {i} (\omega _{\rm {s}}-\omega )}}+{\frac {1}{1/\tau +\mathrm {i} (\omega _{\rm {s}}+\omega )}}\right)\\&={\frac {x_{0}}{\sqrt {2\pi }}}{\frac {1/\tau +\mathrm {i} \omega }{(1/\tau +\mathrm {i} \omega )^{2}+\omega _{\rm {s}}^{2}}}\,.\end{aligned}}$

Eigenschaften

Linearität

Die Fourier-Transformation${\mathcal {F}}$ist einlinearer Operator.Das heißt, es gilt ${\mathcal {F}}(a\cdot f+b\cdot g)=a\cdot {\mathcal {F}}(f)+b\cdot {\mathcal {F}}(g)$.

Stetigkeit

Die Fourier-Transformation ist ein stetiger Operator vomRaum der integrierbaren Funktionen$L^{1}(\mathbb {R} ^{n})$in denRaum der Funktionen$C_{0}(\mathbb {R} ^{n})$,die im Unendlichen verschwinden.Mit$C_{0}(\mathbb {R} ^{n})$ist die Menge der stetigen Funktionen bezeichnet, welche für$|x|\to \infty$verschwinden. Die Tatsache, dass die Fourier-Transformierten im Unendlichen verschwinden, ist auch alsLemma von Riemann-Lebesguebekannt. Außerdem gilt die Ungleichung

$\|{\mathcal {F}}f\|_{L^{\infty }(\mathbb {R} ^{n})}\leq {\frac {1}{({\sqrt {2\pi }})^{n}}}\|f\|_{L^{1}(\mathbb {R} ^{n})}$.

Differentiationsregeln

Sei$f\in S(\mathbb {R} ^{n})\subset L^{1}(\mathbb {R} ^{n})$eineSchwartz-Funktionund$\alpha \in \mathbb {N} _{0}^{n}$einMultiindex.Dann gilt

• ${\mathcal {F}}f\in S(\mathbb {R} ^{n})$und$D^{\alpha }({\mathcal {F}}f)=(-{\rm {i}})^{|\alpha |}{\mathcal {F}}(x^{\alpha }f)$.
• $({\mathcal {F}}(D^{\alpha }f))(\xi )={\rm {i}}^{|\alpha |}\xi ^{\alpha }({\mathcal {F}}f)(\xi )$.

Fixpunkt

Die Dichtefunktion

$\varphi (x)={\frac {1}{(2\pi )^{n/2}}}\cdot \mathrm {e} ^{-{\frac {1}{2}}\|x\|^{2}}$

mit$x\in \mathbb {R} ^{n}$der ($n$-dimensionalen) Gauß’schenNormalverteilungist einFixpunktder Fourier-Transformation. Das heißt, es gilt für alle$x\in \mathbb {R} ^{n}$die Gleichung

$({\mathcal {F}}\varphi )(x)=\varphi (x)$.

Insbesondere ist also$\varphi$eineEigenfunktionder Fourier-Transformation zumEigenwert$1$.Mit Hilfe desResiduensatzesoder mit Hilfepartieller Integrationund Lösen einer gewöhnlichen Differentialgleichung kann in diesem Fall das Fourier-Integral$\textstyle {\tfrac {1}{(2\pi )^{n}}}\int _{\mathbb {R} ^{n}}\mathrm {e} ^{{\rm {i}}x\cdot \xi }\mathrm {e} ^{-{\frac {1}{2}}x^{2}}\mathrm {d} x$bestimmt werden.

Spiegelsymmetrie

Für$f\in S(\mathbb {R} ^{n})$gilt für alle$x\in \mathbb {R} ^{n}$die Gleichung

$({\mathcal {F}}^{2}f)(x)=({\mathcal {F}}({\mathcal {F}}f))(x)=f(-x)$.

Äquivalent lässt sich dies auf dem Schwartzraum$S(\mathbb {R} ^{n})$als Operatorgleichung

${\mathcal {F}}^{2}={\mathcal {P}}$

schreiben, wobei

${\mathcal {P}}:f\mapsto (x\mapsto f(-x))$

den Paritätsoperator bezeichnet.

Rücktransformationsformel

Sei$f\in L^{1}(\mathbb {R} ^{n})$eine integrierbare Funktion derart, dass auch${\mathcal {F}}(f)\in L^{1}(\mathbb {R} ^{n})$gilt. Dann gilt die Rücktransformation

${\mathcal {F}}^{-1}({\mathcal {F}}(f))(x)=f(x)={\frac {1}{(2\pi )^{\frac {n}{2}}}}\int _{\mathbb {R} ^{n}}\mathrm {e} ^{\mathrm {i} tx}{\mathcal {F}}(f)(t)\,\mathrm {d} t.$

Diese wird auchFouriersynthesegenannt. Auf demSchwartz-Raum$S(\mathbb {R} ^{n})$ist die Fouriertransformation einAutomorphismus.

Faltungstheorem

DasFaltungstheoremfür die Fourier-Transformation besagt, dass dieFaltungzweier Funktionen durch die Fourier-Transformation in ihrem Bildraum in eine Multiplikation reeller Zahlen überführt wird. Für$f,g\in L^{1}(\mathbb {R} ^{n})$gilt also

${\mathcal {F}}(f*g)=(2\pi )^{\tfrac {n}{2}}\,{\mathcal {F}}(f)\cdot {\mathcal {F}}(g)$.

Die Umkehrung des Faltungssatzes besagt

${\mathcal {F}}(f)*{\mathcal {F}}(g)=(2\pi )^{\tfrac {n}{2}}{\mathcal {F}}(f\cdot g)$.

Fourier-Transformation von L²-Funktionen

Definition

Für eine Funktion$f\in L^{2}(\mathbb {R} ^{n})$ist die Fouriertransformation mittels eines Dichtheitsargumentes definiert durch

${\mathcal {F}}(f)(\xi )=\lim _{r\to \infty }{\frac {1}{\left(2\pi \right)^{\frac {n}{2}}}}\int _{B_{r}(0)}f(x)\mathrm {e} ^{-\mathrm {i} x\xi }\mathrm {d} x$.

Die Konvergenz ist im Sinne von$L^{2}$zu verstehen und$B_{r}(0)=\{x\in \mathbb {R} ^{n}:|x|\leq r\}$ist die Kugel um den Ursprung mit Radius$r$.Für Funktionen$f\in L^{2}(\mathbb {R} ^{n})\cap L^{1}(\mathbb {R} ^{n})$stimmt diese Definition mit der aus dem ersten Abschnitt überein. Da die Fouriertransformation bezüglich des$L^{2}$-Skalarproduktes unitär ist (s. u.) und $L^{2}(\mathbb {R} ^{n})\cap L^{1}(\mathbb {R} ^{n})$in$L^{2}(\mathbb {R} ^{n})$dicht liegt, folgt, dass die Fouriertransformation ein isometrischer Automorphismus des$L^{2}(\mathbb {R} ^{n})$ist. Dies ist die Aussage desSatzes von Plancherel.

Hausdorff-Young-Ungleichung

Seien$1\leq p\leq 2$und${\tfrac {1}{p}}+{\tfrac {1}{q}}=1$.Für$f\in L^{p}(\mathbb {R} ^{n})$ist${\mathcal {F}}(f)\in L^{q}(\mathbb {R} ^{n})$und es gilt

$\|{\mathcal {F}}(f)\|_{L^{q}(\mathbb {R} ^{n})}\leq {\frac {1}{(2\pi )^{n\left({\frac {1}{p}}-{\frac {1}{2}}\right)}}}\|f\|p(\mathbb {R} ^{n})$.

Die Fourier-Transformation${\mathcal {F}}:L^{2}(\mathbb {R} ^{n})\to L^{2}(\mathbb {R} ^{n})$hat also eineFortsetzungzu einem stetigen Operator${\mathcal {F}}:L^{p}(\mathbb {R} ^{n})\to L^{q}(\mathbb {R} ^{n})$,der durch

${\mathcal {F}}(f)(\xi )=\lim _{r\to \infty }{\frac {1}{(2\pi )^{\frac {n}{2}}}}\int _{B_{r}(0)}f(x)\mathrm {e} ^{-\mathrm {i} x\xi }\mathrm {d} x$

beschrieben wird. Der Grenzwert ist hier im Sinne von$L^{q}$zu verstehen.

Differentiationsregel

Falls die Funktion$f$schwach differenzierbar ist, gibt es eine Differentiationsregel analog zu denen für Schwartzfunktionen. Sei also$f\in W^{k,2}(\mathbb {R} ^{n})=H^{k}(\mathbb {R} ^{n})$einek-mal schwach differenzierbare L²-Funktionund$\alpha$einMultiindexmit$|\alpha |\leq k$.Dann gilt

${\mathcal {F}}(D^{\alpha }f)(\xi )=\mathrm {i} ^{|\alpha |}\xi ^{\alpha }{\mathcal {F}}(f)(\xi )$.

Unitäre Abbildung

Die Fourier-Transformation ist bezüglich des komplexen$L^{2}$-Skalarproduktes einunitärer Operator,das heißt, es gilt

$\langle {\mathcal {F}}(f),g\rangle _{L^{2}}=\int _{\mathbb {R} ^{n}}{\overline {{\mathcal {F}}(f)}}(x)g(x)\mathrm {d} x=\int _{\mathbb {R} ^{n}}{\overline {f}}(x){\mathcal {F}}^{-1}(g)(x)\mathrm {d} x=\langle f,{\mathcal {F}}^{-1}(g)\rangle _{L^{2}}.$

Damit liegt dasSpektrumder Fourier-Transformation auf derEinheitskreislinie.Im eindimensionalen Fall ($n=1$) bilden ferner dieHermite-Funktionen$\left(h_{n}\right)_{n\in \mathbb {N} _{0}}$imRaum$L^{2}\left(\mathbb {R} \right)$einvollständiges OrthonormalsystemvonEigenfunktionenzu den Eigenwerten$\left(-\mathrm {i} \right)^{n}$.

Fourier-Transformation im Raum der temperierten Distributionen

→Hauptartikel:Temperierte Distribution

Sei$u\in S'(\mathbb {R} ^{n})$eine temperierte Distribution, die Fourier-Transformierte${\mathcal {F}}(u)$ist für alle$\phi \in S(\mathbb {R} ^{n})$definiert durch

${\mathcal {F}}(u)(\phi ):=u({\mathcal {F}}(\phi ))$.

Stattet man den Raum$S'(\mathbb {R} ^{n})$mit derSchwach-*-Topologieaus, dann ist die Fourier-Transformation eine stetige, bijektive Abbildung auf$S'(\mathbb {R} ^{n})$.Ihre Umkehrabbildung lautet

$u(\phi )(-x)={\frac {1}{(2\pi )^{n}}}{\mathcal {F}}({\mathcal {F}}(u))(\phi )(x)$.

Fourier-Transformation von Maßen

Die Fourier-Transformation wird allgemein für endlicheBorel-Maßeauf$\mathbb {R} ^{n}$definiert:

${\check {\mu }}(x)=\int \mathrm {e} ^{\mathrm {i} xy}\mu (\mathrm {d} y)$

heißtinverse Fourier-Transformiertedes Maßes. Diecharakteristische Funktionist dann die inverse Fourier-Transformierte einerWahrscheinlichkeitsverteilung.

Partielle Differentialgleichungen

In derTheorie der partiellen Differentialgleichungenspielt die Fourier-Transformation eine wichtige Rolle. Mit ihrer Hilfe kann man Lösungen bestimmter Differentialgleichungen finden. DieDifferentiationsregelund dasFaltungstheoremsind dabei von essentieller Bedeutung. Am Beispiel derWärmeleitungsgleichungwird nun gezeigt, wie man mit der Fourier-Transformation eine partielle Differentialgleichung löst. Das Anfangswertproblem der Wärmegleichung lautet

$\left\{{\begin{array}{rcll}{\frac {\partial u}{\partial t}}(x,t)&=&\Delta _{x}u(x,t)&{\text{in }}\mathbb {R} ^{n}\times ]0,\infty [\\u(x,t)&=&g(x,t)&{\text{auf }}\mathbb {R} ^{n}\times \{t=0\}\,.\end{array}}\right.$

Hierbei bezeichnet$\Delta _{x}$denLaplace-Operator,der nur auf die$x$-Variablen wirkt. Anwenden der Fourier-Transformation auf beide Gleichungen bezüglich der$x$-Variablen und Anwenden der Differentiationsregel ergibt

$\left\{{\begin{array}{rcll}{\mathcal {F}}\left({\frac {\partial u}{\partial t}}\right)(\xi,t)&=&-|\xi |^{2}{\mathcal {F}}(u)(\xi,t)&{\text{in }}\mathbb {R} ^{n}\times ]0,\infty [\\{\mathcal {F}}(u)(\xi,t)&=&{\mathcal {F}}(g)(\xi,t)&{\text{auf }}\mathbb {R} ^{n}\times \{t=0\}\,.\end{array}}\right.$

Hierbei handelt es sich nun um einegewöhnliche Differentialgleichung,die die Lösung

${\mathcal {F}}(u)(\xi,t)=\mathrm {e} ^{-t|\xi |^{2}}{\mathcal {F}}(g)(\xi,t)$

hat. Daraus folgt$\textstyle u(x,t)={\mathcal {F}}^{-1}\left(\exp(-t|\xi |^{2}){\mathcal {F}}(g)\right)(x,t)$und aufgrund des Faltungstheorems gilt

$u(x,t)={\frac {g(x,t)*F(x,t)}{(2\pi )^{\frac {n}{2}}}}$

mit${\mathcal {F}}(F)(\xi,t)=\exp(-t|\xi |^{2}).$Daraus folgt

$F(x,t)={\frac {1}{(2\pi )^{\frac {n}{2}}}}\int _{\mathbb {R} ^{n}}\mathrm {e} ^{\mathrm {i} x\cdot y-t|y|^{2}}\mathrm {d} y={\frac {1}{(2t)^{\frac {n}{2}}}}\mathrm {e} ^{\frac {-|x|^{2}}{4t}}\,.$

Das ist dieFundamentallösungder Wärmegleichung. Die Lösung des hier betrachteten Anfangswertproblems hat daher die Darstellung

$u(x,t)={\frac {g(x,t)*F(x,t)}{(2\pi )^{\frac {n}{2}}}}={\frac {1}{(4\pi t)^{\frac {n}{2}}}}\int _{\mathbb {R} ^{n}}\mathrm {e} ^{-{\frac {|x-\xi |^{2}}{4t}}}g(\xi )\mathrm {d} \xi \,.$

Tabelle wichtiger Fourier-Transformations-Paare

In diesem Kapitel folgt eine Zusammenstellung wichtiger Fourier-Transformations-Paare.

Signal	Fouriertransformierte Kreisfrequenz	Fouriertransformierte Frequenz	Hinweise
$g(t)$	$G(\omega )={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }g(t)\mathrm {e} ^{-\mathrm {i} \omega t}\mathrm {d} t$	$G(f)=\int _{-\infty }^{\infty }g(t)\mathrm {e} ^{-\mathrm {i} 2\pi ft}\mathrm {d} t$
$g(t-a)$	$\mathrm {e} ^{-\mathrm {i} a\omega }G(\omega )$	$\mathrm {e} ^{-\mathrm {i} 2\pi af}G(f)$	Zeitverschiebung
$\mathrm {e} ^{\mathrm {i} at}g(t)$	$G(\omega -a)$	$G\left(f-{\frac {a}{2\pi }}\right)$	Frequenzverschiebung
$g(at)$	${\frac {1}{|a|}}G\left({\frac {\omega }{a}}\right)$	${\frac {1}{|a|}}G\left({\frac {f}{a}}\right)$	Frequenzskalierung
$g^{(n)}(t)$	$(\mathrm {i} \omega )^{n}G(\omega )$	$(\mathrm {i} 2\pi f)^{n}G(f)$	Hier ist$n$einenatürliche Zahlund g eineSchwartz-Funktion.$g^{(n)}$bezeichnet die$n$-te Ableitung von g.

Quadratisch integrierbare Funktionen

Signal	Fouriertransformierte Kreisfrequenz	Fouriertransformierte Frequenz	Hinweise
$g(t)$	$G(\omega )={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }g(t)\mathrm {e} ^{-\mathrm {i} \omega t}\mathrm {d} t$	$G(f)=\int _{-\infty }^{\infty }g(t)\mathrm {e} ^{-\mathrm {i} 2\pi ft}\mathrm {d} t$
$\exp \left(-{\frac {at^{2}}{2}}\right)$	${\frac {1}{\sqrt {a}}}\cdot \exp \left(-{\frac {\omega ^{2}}{2a}}\right)$	${\sqrt {\frac {2\pi }{a}}}\exp \left(-{\frac {2\pi }{a}}\cdot \pi f^{2}\right)$	Die Gaußsche Funktion$\exp(-t^{2}/2)$ergibt fouriertransformiert wieder dieselbe Funktion. Für die Integrierbarkeit muss$\mathrm {Re} (a)>0$sein.
$\operatorname {rect} (at)$	${\frac {1}{{\sqrt {2\pi }}|a|}}\cdot \operatorname {sinc} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{|a|}}\cdot \operatorname {sinc} \left({\frac {f}{a}}\right)$	DieRechteckfunktionund diesinc-Funktion($\operatorname {sinc} (x)=\sin(\pi x)/(\pi x)$).
$\operatorname {sinc} (at)$	${\frac {1}{{\sqrt {2\pi }}|a|}}\cdot \operatorname {rect} \left({\frac {\omega }{2\pi a}}\right)$	${\frac {1}{|a|}}\cdot \operatorname {rect} \left({\frac {f}{a}}\right)$	Die Rechteckfunktion ist ein idealisierter Tiefpassfilter, und die sinc-Funktion ist die akausale Stoßantwort eines solchen Filters ($\operatorname {sinc} (x)=\sin(\pi x)/(\pi x)$).
$\exp \left(-a|t|\right)$	${\sqrt {\frac {2}{\pi }}}{\frac {a}{\omega ^{2}+a^{2}}}$	${\frac {2a}{(2\pi f)^{2}+a^{2}}}$	$a>0.$Die FT der um den Ursprungexponentiellabfallenden Funktion ist eineLorentzkurve.
${\frac {1}{t^{2}+a^{2}}}$	${\sqrt {\frac {\pi }{2}}}{\frac {1}{a}}\exp \left(-a|\omega |\right)$	${\frac {\pi }{a}}\exp \left(-2\pi a|f|\right)$

Distributionen

Signal	Fouriertransformierte Kreisfrequenz	Fouriertransformierte Frequenz	Hinweise
$g(t)$	$G(\omega )={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }g(t)\mathrm {e} ^{-\mathrm {i} \omega t}\mathrm {d} t$	$G(f)=\int _{-\infty }^{\infty }g(t)\mathrm {e} ^{-\mathrm {i} 2\pi ft}\mathrm {d} t$
$\mathrm {e} ^{\mathrm {i} at}$	${\sqrt {2\pi }}\cdot \delta (\omega -a)$	$\delta \left(f-{\frac {a}{2\pi }}\right)$
$\cos(at)$	${\sqrt {2\pi }}{\frac {\delta (\omega -a)+\delta (\omega +a)}{2}}$	${\frac {\delta (f-{\frac {a}{2\pi }})+\delta (f+{\frac {a}{2\pi }})}{2}}$
$\sin(at)$	${\sqrt {2\pi }}{\frac {\delta (\omega -a)-\delta (\omega +a)}{2\mathrm {i} }}$	${\frac {\delta (f-{\frac {a}{2\pi }})-\delta (f+{\frac {a}{2\pi }})}{2\mathrm {i} }}$
$t^{n}$	$\mathrm {i} ^{n}{\sqrt {2\pi }}\delta ^{(n)}(\omega )$	$\left({\frac {\mathrm {i} }{2\pi }}\right)^{n}\delta ^{(n)}(f)$	Hier ist$n$einenatürliche Zahlund$\delta ^{(n)}$die$n$-te Ableitung derDelta-Distribution.
${\frac {1}{t^{n}}}$	$-\mathrm {i} {\sqrt {\frac {\pi }{2}}}\cdot {\frac {(-\mathrm {i} \omega )^{n-1}}{(n-1)!}}\operatorname {sgn}(\omega )$	$-\mathrm {i} \pi {\frac {(-\mathrm {i} 2\pi f)^{n-1}}{(n-1)!}}\operatorname {sgn}(f)$
$\operatorname {sgn}(t)$	${\sqrt {\frac {2}{\pi }}}\cdot {\frac {1}{\mathrm {i} \ \omega }}$	${\frac {1}{\mathrm {i} \pi f}}$
$\Theta (t)$	${\sqrt {\frac {\pi }{2}}}\left({\frac {1}{\mathrm {i} \pi \omega }}+\delta (\omega )\right)$	${\frac {1}{2}}\left({\frac {1}{\mathrm {i} \pi f}}+\delta (f)\right)$	$\Theta (t)$ist der Einheitssprung (Heaviside-Funktion).
$\sum _{n=-\infty }^{\infty }\delta (t-nT)$	${\frac {2\pi }{T}}\sum _{k=-\infty }^{\infty }\delta \left(\omega -k{\frac {2\pi }{T}}\right)$	${\frac {1}{T}}\sum _{k=-\infty }^{\infty }\delta \left(f-{\frac {k}{T}}\right)$	Das Signal heißtDirac-Kamm.

Siehe auch

• Diskrete Fourier-Transformation
• Kurzzeit-Fourier-Transformation
• Fouriertransformation für zeitdiskrete Signale
• Schnelle Fourier-Transformation
• Inverse schnelle Fourier-Transformation

Literatur

• Rolf Brigola:Fourier-Analysis und Distributionen.edition swk, Hamburg 2013,ISBN 978-3-8495-2892-8.
• S. Bochner,K. Chandrasekharan:Fourier Transforms.Princeton University Press, Princeton NJ 1949 (Annals of mathematics studies19,ISSN0066-2313).
• Otto Föllinger:Laplace-, Fourier- und z-Transformation.Bearbeitet von Mathias Kluwe. 8. überarbeitete Auflage. Hüthig, Heidelberg 2003,ISBN 3-7785-2911-0(Studium).
• Lars Hörmander:The Analysis of Linear Partial Differential Operators I.Second Edition. Springer-Verlag,ISBN 3-540-52345-6.
• Burkhard Lenze:Einführung in die Fourier-Analysis.3. durchgesehene Auflage. Logos Verlag, Berlin 2010,ISBN 3-931216-46-2.
• M. J. Lighthill:Introduction to Fourier Analysis and Generalised Functions.Cambridge University Press, Cambridge 2003,ISBN 0-521-09128-4(Cambridge Monographs on Mechanics and Applied Mathematics).
• P. I. Lizorkin:Fourier Transform.In:Michiel Hazewinkel(Hrsg.):Encyclopedia of Mathematics.Springer-Verlag undEMSPress, Berlin 2002,ISBN 1-55608-010-7(englisch,encyclopediaofmath.org).
• Athanasios Papoulis:The Fourier Integral and Its Applications.Reissued. McGraw-Hill, New York NY u. a. 1987,ISBN 0-07-048447-3(McGraw-Hill Classic Textbook Reissue Series).
• Lothar Papula:Mathematische Formelsammlung.11. Auflage. Springer Verlag. Wiesbaden 2014,ISBN 978-3-8348-2311-3.
• Herbert Sager:Fourier-Transformation.1. Auflage. vdf Hochschulverlag AG an der ETH Zürich, Zürich 2012,ISBN 978-3-7281-3393-9.
• Elias M. Stein,Rami Shakarchi:Princeton Lectures in Analysis.Band 1:Fourier Analysis. An Introduction.Princeton University Press, Princeton NJ 2003,ISBN 0-691-11384-X.
• Dirk Werner:Funktionalanalysis.Springer-Verlag, 6. Auflage,ISBN 978-3-540-72533-6.
• Jörg Lange,Tatjana Lange:Fourier-Transformation zur Signal- und Systembeschreibung. Kompakt, visuell, intuitiv verständlich.Springer Vieweg, 2019,ISBN 978-3-658-24849-9.

Weblinks

Commons:Fourier transformation– Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein:Fourier Transform.In:MathWorld(englisch).
• Was ist eine Fourier-Transformation? Eine visuelle EinführungaufYouTube,abgerufen am 15. April 2023.