Hidden Markov Model

DasHidden Markov Model,kurzHMM(deutschverdecktes Markowmodell,oderverborgenes Markowmodell) ist einstochastischesModell,in dem ein System durch eineMarkowkette– benannt nach dem russischen MathematikerA. A. Markow– mit unbeobachteten Zuständen modelliert wird. Ein HMM kann dadurch als einfachster Spezialfall einesdynamischen bayesschen Netzesangesehen werden.

Die Modellierung als Markowkette bedeutet, dass das System auf zufällige Weise von einem Zustand in einen anderen übergeht, wobei dieÜbergangswahrscheinlichkeitennur jeweils vom aktuellen Zustand abhängen, aber nicht von den davor eingenommenen Zuständen. Außerdem wird angenommen, dass die Übergangswahrscheinlichkeiten über die Zeit konstant sind. Bei einem HMM werden jedoch nicht die Zustände selbst von außen beobachtet; sie sindverborgen(engl.hidden,siehe auchLatentes Variablenmodell). Stattdessen sind jedem dieser inneren Zustände beobachtbare Ausgabesymbole (sogenannteEmissionen) zugeordnet, die je nach Zustand mit gewissen Wahrscheinlichkeiten auftreten. Die Aufgabe besteht meist darin, aus der beobachteten Sequenz der Emissionen zuwahrscheinlichkeitstheoretischenAussagen über die verborgenen Zustände zu kommen.

Da die Markowmodelle eng verwandt mit den in der Regelungstechnik verwendeten Zustandsraummodellen sind, ist darauf zu achten, dass der Begriff „beobachten “nicht mit dem regelungstechnischen Begriff der „Beobachtbarkeit“,der vonRudolf Kálmán1960 eingeführt wurde und eine eigenständige Systemeigenschaft beschreibt, verwechselt wird. „Beobachten “im Sinn der Markowmodelle wird in der Regelungstechnik mit „messen “bezeichnet. Die im Sinn der Markowtheorie „unbeobachteten “oder „hidden “Zustände können sehr wohl im Sinne der Regelungstechnik beobachtbar sein, müssen es aber nicht.

Wichtige Anwendungsgebiete sindSprach-undSchrifterkennung,ComputerlinguistikundBioinformatik,Spamfilter,Gestenerkennungin derMensch-Maschine-Kommunikation,physikalische ChemieundPsychologie.

Markowansatz

Gegeben seien zweizeitdiskrete Zufallsprozesse$\{X_{t}\}_{t\in \mathbb {N} }$und$\{Y_{t}\}_{t\in \mathbb {N} }$,von denen nur der letzte beobachtbar sei. Durch ihn sollen Rückschlüsse auf den Verlauf des ersten Prozesses gezogen werden; hierfür wird ein mathematisches Modell benötigt, das die beiden Prozesse miteinander in Beziehung setzt.

Der hier beschriebene Ansatz zeichnet sich durch die folgenden beiden Annahmen aus:

1. Markoweigenschaft

Der aktuelle Wert des ersten Prozesses hängt ausschließlich von seinem letzten Wert ab:

$\forall t\in \mathbb {N} \colon P(X_{t}=x_{t}|X_{1}=x_{1};\ldots;X_{t-1}=x_{t-1};Y_{1}=y_{1};\ldots;Y_{t-1}=y_{t-1})=P(X_{t}=x_{t}|X_{t-1}=x_{t-1})$.

2. Markoweigenschaft

Der aktuelle Wert des zweiten Prozesses hängt ausschließlich vom aktuellen Wert des ersten ab:

$\forall t\in \mathbb {N} \colon P(Y_{t}=y_{t}|X_{1}=x_{1};\ldots;X_{t}=x_{t};Y_{1}=y_{1};\ldots;Y_{t-1}=y_{t-1})=P(Y_{t}=y_{t}|X_{t}=x_{t})$.

Haben die beiden Prozesse nun noch jeweils einenendlichenWertevorrat, so lässt sich das so gewonnene Modell alsprobabilistischerAutomatauffassen, genauer alsMarkow-Kette. Man sagt auch$\{X_{t}\}$ist einMarkow-Prozess. Angelehnt an den Sprachgebrauch in dertheoretischen Informatik– insbesondere derAutomatentheorieund derTheorie formaler Sprachen– heißen die Werte des ersten ProzessesZuständeund die des zweitenEmissionenbzw.Ausgaben.

Definition

Parameter eines Hidden Markov Model (Beispiel)
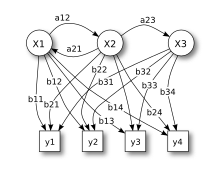
x– (verborgene) Zustände
y– mögliche Beobachtungen (Emissionen)
a– Übergangswahrscheinlichkeiten
b– Emissionswahrscheinlichkeiten

EinHidden Markov Modelist ein 5-Tupel$\lambda =(S;V;A;B;\pi )$mit:

• $S=\{s_{1};\dotsc;s_{n}\}$der Menge allerZustände,das sind die möglichen Werte derZufallsvariablen$X_{t}$,
• $V=\{v_{1};\dotsc;v_{m}\}$dasAlphabetder möglichen Beobachtungen – dieEmissionender$Y_{t}$,
• $A\in \mathbb {R} ^{n\times n}$dieÜbergangsmatrixzwischen den Zuständen,$a_{ij}=P(X_{t}=s_{j}|X_{t-1}=s_{i})$gibt dabei jeweils dieWahrscheinlichkeitan, dass vom Zustand$s_{i}$in den Zustand$s_{j}$gewechselt wird,
• $B\in \mathbb {R} ^{n\times m}$die Beobachtungsmatrix, die$b_{ij}=P(Y_{t}=v_{j}|X_{t}=s_{i})$geben die Wahrscheinlichkeit an, im Zustand$s_{i}$die Beobachtung$v_{j}$zu machen, sowie
• $\pi \in \mathbb {R} ^{n}$die Anfangsverteilung,$\pi _{i}=P(X_{1}=s_{i})$ist die Wahrscheinlichkeit, dass$s_{i}$der Startzustand ist.

Ein HMM heißestationär(oder auchzeitinvariant), wenn sich die Übergangs- und Emissionswahrscheinlichkeiten nicht mit der Zeit ändern. Diese Annahme ist oft sinnvoll, weil auch die modellierten Naturgesetze konstant sind.

Veranschaulichung

Zeitliche Entwicklung eines HMM

Das Bild zeigt die generelle Architektur eines instanziierten HMMs. Jedes Oval ist die Repräsentation einer zufälligen Variable$x(t)$oder$y(t)$,welche beliebige Werte aus$S$bzw.$V$annehmen kann. Die erste Zufallsvariable ist dabei der versteckte Zustand des HMMs zum Zeitpunkt$t$,die zweite ist die Beobachtung zu diesem Zeitpunkt. Die Pfeile in demTrellis-Diagrammbedeuten einebedingte Abhängigkeit.

Im Diagramm sieht man, dass der Zustand der versteckten Variable$x(t)$nur vom Zustand der Variable$x(t-1)$abhängt, frühere Werte haben keinen weiteren Einfluss. Deshalb ist das Modell ein Markov-Modell 1. Ordnung. Sollten höhere Ordnungen benötigt werden, so können diese durch das Einfügen neuer versteckter Zustände stets auf die 1. Ordnung zurückgeführt werden. Der Wert von$y(t)$hängt weiter ausschließlich von$x(t)$ab.

Beispiel

Gefangener im Verlies

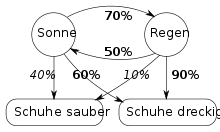
Ein Gefangener im Kerkerverlies möchte das aktuelle Wetter herausfinden. Er weiß, dass auf einen sonnigen Tag zu 70 % ein Regentag folgt und dass auf einen Regentag zu 50 % ein Sonnentag folgt. Weiß er zusätzlich, dass die Schuhe der Wärter bei Regen zu 90 % dreckig, bei sonnigem Wetter aber nur zu 60 % dreckig sind, so kann er durch Beobachtung der Wärterschuhe Rückschlüsse über das Wetter ziehen (das heißt, er kann die Wahrscheinlichkeit für Regenwetter gegenüber sonnigem Wetter abschätzen). Hier bildet das tatsächlich vorhandene, aber nicht sichtbare Wetter den zu ermittelnden versteckten Zustand, die Prozentwerte 70 % und 50 % sind (über längere Zeiten hinweg ermittelte) Trainingsdaten des Modells, und die tatsächlich beobachtbaren Zustände liegen im jeweiligen Aussehen der Schuhe.

Aus den Übergangswahrscheinlichkeiten$a_{ij}$ergibt sich (langfristig, also ohne den Anfangszustand eingehen zu lassen) die Wahrscheinlichkeit für Sonne von$p_{\mathrm {S} }=50\%/(50\%+70\%)\approx 41{,}7\%$und für Regen von$p_{\mathrm {R} }=1-p_{\mathrm {S} }\approx 58{,}3\%$.Damit ergeben sich die Kombinationen von Zuständen mit den Wahrscheinlichkeiten:

	Sonne	Regen
Saubere Schuhe	$0{,}4\cdot p_{\mathrm {S} }\approx 16{,}7\%$	$0{,}1\cdot p_{\mathrm {R} }\approx 5{,}8\%$
Dreckige Schuhe	$0{,}6\cdot p_{\mathrm {S} }\approx 25{,}0\%$	$0{,}9\cdot p_{\mathrm {R} }\approx 52{,}5\%$

Wenn ein Wärter saubere Schuhe hat, ist die Wahrscheinlichkeit von sonnigem Wetter damit$0{,}4\cdot p_{\mathrm {S} }/(0{,}4\cdot p_{\mathrm {S} }+0{,}1\cdot p_{\mathrm {R} })\approx 74{,}1\%$und entsprechend ist bei dreckigen Schuhen die Regenwahrscheinlichkeit etwa 67,9 %. Außerdem müssten die Wärter im Mittel zu$0{,}4\cdot p_{\mathrm {S} }+0{,}1\cdot p_{\mathrm {R} }=22{,}5\%$der Tage saubere Schuhe haben, andernfalls kann sich der Gefangene überlegen, welche Parameter angepasst werden sollten, damit sein Modell stimmt.

So weit kann der Gefangene aus der Beobachtung an einem einzelnen Tag schließen. Dabei berücksichtigt er nicht die konkreten Wahrscheinlichkeiten des Wechsels von sonnigen und verregneten Tagen. Bezieht er diese mit ein, so kommt er mit demViterbi-Algorithmuszu einem etwas genaueren Ergebnis.

DNA-Sequenz: CpG-Inseln aufspüren

Zur Untersuchung von DNA-Sequenzen mit bioinformatischen Methoden kann das HMM verwendet werden. Beispielsweise lassen sich soCpG-Inselnin einer DNA-Sequenz aufspüren. Dies sind Bereiche einesDNS-Einzelstrangs mit einem erhöhten Anteil von aufeinanderfolgendenCytosin- undGuanin-Nukleinbasen.Dabei stellt die DNS-Sequenz die Beobachtung dar, deren Zeichen$V=\{A,C,G,T\}$bilden das Ausgabealphabet. Im einfachsten Fall besitzt das HMM zwei verborgene Zustände, nämlichCpG-Inselundnicht-CpG-Insel.Diese beiden Zustände unterscheiden sich in ihrer Ausgabeverteilung, so dass zum ZustandCpG-Inselmit größerer Wahrscheinlichkeit Zeichen$C$und$G$ausgegeben werden.

Spracherkennung

In der automatischen Spracherkennung mit HMM werden diegesprochenenLauteals versteckte Zustände aufgefasst und die tatsächlichhörbarenTöneals Emission.

Problemstellungen

Im Zusammenhang mit HMMs existieren mehrere grundlegende Problemstellungen.

Bestimmen der Modellgröße

Gegeben sind die beobachtbaren Emissionen$V$. Es ist zu klären, welche Modelleigenschaften – insbesondere welcheorthogonaleDimensionalität – den Schluss auf die nicht direkt beobachtbaren Zustände erlauben und gleichzeitig eine sinnvolleBerechenbarkeitzulassen. Insbesondere ist zu entscheiden, welche Laufzeit für die Modellrechnungen erforderlich werden darf, um die Verwendbarkeit der Schätzungen zu erhalten.

Implementierung

Die Berechnung der Schätzwerte der nicht beobachtbaren Zustände aus den beobachtbaren Ausgabesequenzen muss die erreichbaren numerischen Genauigkeiten beachten. Weiter müssen Kriterien zur Klassifizierung derstatistischen Signifikanzimplementiert werden. Bei Verwendung eines HMM für einen bestimmten Merkmalsvektor bestimmt die Signifikanz die Wahrscheinlichkeit einer zutreffenden oder falschen Modellhypothese sowie derenInformationsgehalt(Entropie,bedingte Entropie) bzw. derenInformationsqualität.

Filtern

Gegeben sei ein HMM$\lambda$sowie eine Beobachtungssequenz${\boldsymbol {o}}\in V^{*}$derLänge$T$. Gesucht ist die Wahrscheinlichkeit$P(X_{T}=s_{i}|{\boldsymbol {o}};\lambda )$,dass der momentane verborgene Zustand zum letzten Zeitpunkt$T$gerade$s_{i}$ist. Ein effizientes Verfahren zur Lösung des Filterungsproblems ist derForward-Algorithmus.

Prädiktion/Vorhersage

Gegeben sei wieder ein HMM$\lambda$und die Beobachtungssequenz${\boldsymbol {o}}$sowie ein$\delta \geq 1$. Gesucht ist Wahrscheinlichkeit$P(X_{T+\delta }=s_{i}|{\boldsymbol {o}};\lambda )$,also die Wahrscheinlichkeit, dass sich das HMM zum Zeitpunkt$T+\delta$im Zustand$s_{i}$befindet, falls die betreffende Ausgabe beobachtet wurde. Prädiktion ist dabei gewissermaßen wiederholtes Filtern ohne neue Beobachtungen und lässt sich auch einfach mit demForward-Algorithmusberechnen.

Glätten

Erneut seien$\lambda$,${\boldsymbol {o}}$und ein$\delta$gegeben. Gesucht ist die Wahrscheinlichkeit$P(X_{T-\delta }=s_{i}|{\boldsymbol {o}};\lambda )$,also die Wahrscheinlichkeit, dass sich das Modell zu einem früheren Zeitpunkt in einem bestimmten Zustand befand, unter der Bedingung, dass${\boldsymbol {o}}$beobachtet wurde. Mithilfe desForward-Backward-Algorithmuskann diese Wahrscheinlichkeit effizient berechnet werden.

Dekodierung

Seien wieder$\lambda$sowie${\boldsymbol {o}}$gegeben. Es soll die wahrscheinlichste Zustandsfolge aus$S^{*}$bestimmt werden, die eine vorgegebene Ausgabesequenz erzeugt haben könnte. Dieses Problem lässt sich effizient mit demViterbi-Algorithmuslösen.

Lernproblem

Gegeben sei nur die Ausgabesequenz${\boldsymbol {o}}$. Es sollen die Parameter eines HMM bestimmt werden, die am wahrscheinlichsten die Ausgabesequenz erzeugen. Dies ist lösbar mit Hilfe desBaum-Welch-Algorithmus.

Interpretationsproblem

Gegeben seien nur die möglichen Ausgaben$V$. Es sollen die Zustände imModellsystemund die korrespondierenden Effekte im realen System identifiziert werden, die die Zustandsmenge$S$des Modells beschreibt. Dazu muss vorweg dieBedeutsamkeitder einzelnen Emissionen bestimmt werden.

Anwendungsgebiete

Anwendung finden HMMs häufig in derMustererkennungbei der Verarbeitung von sequentiellen Daten, beispielsweise bei physikalischenMessreihen,aufgenommenen Sprachsignalen oderProteinsequenzen.Dazu werden die Modelle so konstruiert, dass die verborgenen Zustände semantischen Einheiten entsprechen (z. B.Phonemein derSpracherkennung), die es in den sequentiellen Daten (z. B. Kurzzeit-Spektren des Sprachsignals) zu erkennen gilt. Eine weitere Anwendung besteht darin, für ein gegebenes HMM durch eine Suche in einer Stichprobe von sequentiellen Daten solche Sequenzen zu finden, die sehr wahrscheinlich von diesem HMM erzeugt sein könnten. Beispielsweise kann ein HMM, das mit Vertretern einer Proteinfamilie trainiert wurde, eingesetzt werden, um weitere Vertreter dieser Familie in großen Proteindatenbanken zu finden.

Geschichte

Hidden-Markov-Modelle wurden erstmals vonLeonard E. Baumund anderen Autoren in der zweiten Hälfte der 1960er Jahre publiziert. Eine der ersten Applikationen war ab Mitte der 1970er die Spracherkennung. Seit Mitte der 1980er wurden HMMs für die Analyse vonNukleotid-und Proteinsequenzen eingesetzt und sind seitdem fester Bestandteil derBioinformatik.

Literatur

• R. Merkl, S. Waack:Bioinformatik interaktiv.Wiley-VCH, 2002,ISBN 3-527-30662-5.
• G. A. Fink:Mustererkennung mit Markov-Modellen: Theorie, Praxis, Anwendungsgebiete.Teubner, 2003,ISBN 3-519-00453-4.
• Kai-Fu Lee, Hsiao-Wuen Hon:Speaker-Independent Phone Recognition Using Hidden Markov Models.IEEE Transactions on accoustics, speech and signal processing,Nr.37.IEEE, November 1989,S.1641–1648(englisch, IEEE Nr. 8930533, 0096-3518/89/1100-1641).

Weblinks

• R.v. Handel, 28. Juli 2008:Hidden Markov Models(PDF; 900 kB; 123 Seiten) Lecture Notes Princeton University Juli 2008, abgerufen am 24. Februar 2019.
• E.G. Schukat-Talamazzini, 7. Dezember 2018:Spezielle Musteranalysesysteme(PDF; 1,3 MB; 17 Seiten) Vorlesung im WS 2018 an der Universität Jena. Kap. 5, abgerufen am 24. Februar 2019.
• HMM R-Packagezum Modellieren und Analysieren von Hidden-Markov-Modellen, das unter GPL2 frei verfügbar ist
• HMM Java-Bibliothek, die unter der neuen BSD-Lizenz verfügbar istInternal Server Error
• HMM C-Bibliothek, die unter der LGPL frei verfügbar ist