Kreis

EinKreisist eine ebenegeometrische Figur.Er wird definiert als dieMengealler Punkte einerEbene,die den gleichenAbstandzu einem bestimmten Punkt dieser Ebene (demMittelpunkt) haben.Der Abstand der Kreispunkte zum Mittelpunkt ist derRadiusoderHalbmesserdes Kreises,er ist einepositivereelle Zahl.Der Kreis gehört zu den klassischen undgrundlegenden Objektendereuklidischen Geometrie.

Umgangssprachlich und früher wird mit dem Begriff Kreis häufig auch eine Kreisfläche oder eine rundeScheibebezeichnet.Unter einemKringelversteht man einen kleinen, nicht exakt gezeichneter Kreis bzw. ringförmigen Schnörkel.

Bereits diealten ÄgypterundBabylonierversuchten, denFlächeninhaltdes Kreises näherungsweise zu bestimmen. In der griechischenAntikestieß der Kreis wegen seiner Vollkommenheit auf Interesse.Archimedesversuchte erfolglos, den Kreis mit den WerkzeugenZirkelundLinealin einQuadratmit gleichem Flächeninhalt zu überführen, um so den Flächeninhalt des Kreises bestimmen zu können (sieheQuadratur des Kreises). Erst 1882 konnteFerdinand von Lindemanndurch den Nachweis einer besonderen Eigenschaft derKreiszahl,nämlich derTranszendenz,zeigen, dass diese Aufgabe unlösbar ist.

Worterklärungen

Kreisflächen

Nach der eingangs genannten Definition ist ein Kreis eineKurve,also eineindimensionalesGebilde, und keine zweidimensionaleFläche.Da das Wort „Kreis “aber oft ungenau auch für die eingeschlossene Fläche benutzt wird, verwendet man zur Verdeutlichung häufig die BegriffeKreislinie, KreisrandoderKreisperipherieanstatt Kreis – im Gegensatz zurKreisflächeoderKreisscheibe.Mathematiker unterscheiden dann noch zwischen derabgeschlossenenKreisfläche oder -scheibe und deroffenen(oder demKreisinneren), je nachdem ob die Kreislinie dazugehört oder nicht.

In denElementendesEuklidhingegen wird als Kreis die von der Kurve umschlossene Fläche bezeichnet.

Bogen, Sehne, Sektor, Segment und Ring

Kreisring

Kreisbogen, Kreissektor und Kreissegment

Eine zusammenhängende Teilmenge des Kreises (also der Kreislinie) ist einKreisbogen.EineVerbindungsstreckevon zwei Punkten auf der Kreislinie bezeichnet man alsKreissehne.Zu jeder Sehne gehören zwei Kreisbögen. Die längsten Kreissehnen sind diejenigen, die durch den Mittelpunkt verlaufen, also dieDurchmesser.Die zugehörigen Kreisbögen heißen Halbkreise. Ist die Kreissehne kein Durchmesser, so sind die Kreisbögen unterschiedlich lang.

EinKreissektor(Kreisausschnitt)ist eine Fläche, die von zwei Radien und einem dazwischen liegenden Kreisbogen begrenzt wird. Bilden die zwei Radien einen Durchmesser, wird der Sektor auch als Halbkreis bezeichnet.

Kreissegmente(Kreisabschnitte)werden von einem Kreisbogen und einer Kreissehne eingeschlossen.

EinKreisringentsteht, wenn man aus einem Kreis einen kleineren Kreis mit demselben Mittelpunkt herausschneidet.

Sekante, Tangente und Passante

Für die Lage einerGeradenin Bezug auf einen gegebenen Kreis gibt es drei Möglichkeiten:

Beziehung von Kreis zu Tangente, Passante und Sekante

• Ist der Abstand zwischen Mittelpunkt und Gerade kleiner als der Kreisradius, so haben Kreis und Gerade zwei (verschiedene) Schnittpunkte und man nennt die GeradeSekante(lateinischsecare= schneiden). Manchmal bezeichnet man den Spezialfall einer Sekante, die durch den Mittelpunkt eines Kreises verläuft, alsZentrale.
• Stimmt der Abstand des Mittelpunkts zu der Geraden mit dem Radius überein, so gibt es genau einen gemeinsamen Punkt. Man sagt, dass die Gerade den Kreis berührt, und nennt die Gerade eineTangente(lateinischtangere= berühren). Eine Tangente steht im Berührpunkt senkrecht (orthogonal,normal) zum entsprechenden Radius.
• Wenn der Abstand des Kreismittelpunkts von der Geraden größer ist als der Kreisradius, dann haben Kreis und Gerade keinen Punkt gemeinsam. In diesem Fall bezeichnet man die Gerade alsPassante.Diese Bezeichnung hat keinen unmittelbaren lateinischen Ursprung, sondern wurde wohl nach franz. oder ital.passante= Vorbeigehende gebildet. Die lat. Wurzel istpassus= Schritt.

Formale Definition

Ein Kreis mit Mittelpunkt$M$,Radius$r$und Durchmesser$d$.

In einer Ebene$E$ist ein Kreis$k$mit Mittelpunkt$\mathrm {M} \in E$und Radius$r>0$die Punktmenge

$k=\left\{\mathrm {X} \in E~\vert ~{\overline {\mathrm {MX} }}=r\right\}.$

Dabei ist der Radius$r$eine positive reelle Zahl, und${\overline {\mathrm {MX} }}$bezeichnet die Länge derStrecke$[\mathrm {MX} ]$.

Der doppelte Radius heißtDurchmesserund wird oft mit$d$bezeichnet. Radius$r$und Durchmesser$d$sind durch die Beziehungen$d=2r$oder$r=d/2$miteinander verknüpft.

Manchmal wird auch jedeStrecke,die den Mittelpunkt mit einem Punkt auf der Kreislinie verbindet, alsRadiusbezeichnet, und jede Strecke, die durch den Mittelpunkt geht, und deren beide Endpunkte auf der Kreislinie liegen, alsDurchmesser.Bei dieser Sprechweise ist dieZahl$r$dieLängejedes Radius und die Zahl$d$die Länge jedes Durchmessers.

Die offene Kreisfläche ist formal definiert als die Punktmenge

$\left\{\mathrm {X} \in E~\vert ~{\overline {\mathrm {MX} }}<r\right\},$

die abgeschlossene Kreisscheibe als

$\left\{\mathrm {X} \in E~\vert ~{\overline {\mathrm {MX} }}\leq r\right\}.$

Geschichte

Zeit der Ägypter und Babylonier

Kreis (grün) mit d = 9, Quadrat (gepunktete Linie) umschreibt Kreis, unregelmäßiges Achteck (blau) mit A = 63, Quadrat (rot) mit s = 8/9·d mit A = 64 und Kreis mit A = 63,617...

Annäherung der Kreisfläche im Papyrus Rhind, die obige Figur im Quadrat wird als unregelmäßiges Achteck gedeutet, darunter die Rechenschritte am Beispiel d = 9 (Chet).

Der Kreis gehört neben demPunktund dergeradenLinie zu den ältesten Elementen der vorgriechischen Geometrie.Schon vor viertausend Jahren beschäftigten sich die Ägypter mit ihm in ihren Studien zur Geometrie. Sie konnten den Flächeninhalt$A$eines Kreises näherungsweise bestimmen, indem sie vom Durchmesser d ein Neuntel seiner Länge abzogen und das Ergebnis mit sich selbst multiplizierten. Sie rechneten also

$A\approx \left({\frac {8}{9}}d\right)^{2}={\frac {256}{81}}r^{2}=3{,}16049\dotso \cdot r^{2}$

und bestimmten so näherungsweise (mit einer Abweichung von nur etwa +0,6 %) den Flächeninhalt einer Kreisfläche. Diese Näherung wurde in der altägyptischen AbhandlungPapyrus Rhindgefunden. Sie lässt sich erhalten (siehe nebenstehendes Bild), wenn man den Kreis durch ein unregelmäßiges Achteck annähert.Um die Seite des zum Kreis annähernd flächengleichen Quadrates (rot) rechnerisch zu erhalten, ermittelt man nachKurt Vogelden Flächeninhalt des unregelmäßigen Achtecks und bestimmt aus dessen Wert die nächstliegende Quadratzahl. Die Wurzel daraus ist dann die gesuchte Seitenlänge des flächengleichen Quadrates.

Die Babylonier (1900 bis 1600 vor Christus) benutzten eine ganz andere Methode, um den Flächeninhalt der Kreisscheibe zu berechnen. Im Gegensatz zu den Ägyptern gingen sie vom Kreisumfang$U$aus, den sie als dreimal den Kreisdurchmesser$d$schätzten. Der Flächeninhalt wurde dann auf ein Zwölftel desQuadratesdes Umfanges geschätzt, alsomit einer Abweichung von −4,5 % ein deutlich schlechteres Ergebnis.

In der Technik ermöglicht die kreisrunde Form desRadesdierollendeFortbewegung.

Fragment des Papyrus Rhind

$A\approx {\frac {1}{12}}U^{2}\approx {\frac {9}{12}}d^{2}=3r^{2},$

Die Babylonier beschäftigten sich aber auch schon mit Kreissegmenten. Sie konnten die Länge der Sehne oder die Höhe des Kreissegments (die senkrecht auf der Sehnenmitte stehende Strecke zwischen Sehne und Umfang) berechnen. Damit begründeten sie dieSehnengeometrie,die später vonHipparchweiterentwickelt wurde und dieClaudius Ptolemaiosan den Anfang seines astronomischen LehrbuchesAlmageststellte.

Antike

Titelblatt von Henry Billingsleys englischer Übersetzung derElemente(1570)

Die Griechen werden meist als die Begründer der Wissenschaft von der Natur angesehen. Als der erste bedeutende Philosoph dieser Zeit, der sich mit Mathematik beschäftigte, giltThalesvon Milet (624–546 v. Chr.). Er brachte Wissen über die Geometrie aus Ägypten mit nach Griechenland, wie zum Beispiel die Aussage, dass der Durchmesser den Kreis halbiert. Andere Aussagen zur Geometrie wurden von Thales selbst aufgestellt. Der heutenach Thales benannte Satzbesagt, dassPeripheriewinkelim Halbkreisrechte Winkelsind. Insbesondere war Thales der erste, bei dem der Begriff desWinkelsauftrat.

Die erste bekannte Definition des Kreises geht auf den griechischen PhilosophenPlaton(428/427–348/347 v. Chr.) zurück, die er in seinemDialogParmenidesformulierte:

„Rund ist doch wohl das, dessen äußerste Teile überall vom Mittelpunkt aus gleich weit entfernt sind. “

–Platon:Parmenides

Zirka 300 Jahre vor Christus lebte der griechische MathematikerEuklid von Alexandria.Über ihn selbst ist wenig bekannt, aber sein Werk im Bereich der Geometrie war beachtlich. Sein Name ist heute noch in Zusammenhängen wieeuklidischer Raum,euklidische Geometrieodereuklidische Metrikin Gebrauch. Sein wichtigstes Werk warenDie Elemente,eine dreizehnbändige Abhandlung, in der er dieArithmetikundGeometrieseiner Zeit zusammenfasste und systematisierte. Er folgerte die mathematischen Aussagen ausPostulatenund begründete damit die euklidische Geometrie. Der dritte Band der Elemente beschäftigte sich mit der Lehre über den Kreis.

VonArchimedes,der vermutlich zwischen 287 v. Chr. und 212 v. Chr. auf Sizilien lebte, ist eine ausführliche Abhandlung mit dem TitelDie Kreismessungüberliefert.Er bewies in dieser Arbeit, dass der Flächeninhalt eines Kreises (A_K) gleich dem Flächeninhalt eines rechtwinkligen Dreiecks (A_D) mit dem Kreisradius (r) als der einen und dem Kreisumfang (U_K) als der anderenKatheteist. Der Flächeninhalt des Kreises lässt sich also als½ · Umfang · Radiusangeben (s. Bild).Mit dieser Erkenntnis führte er das Problem derQuadratur des Kreisesauf die Frage der Konstruierbarkeit des Umfangs aus dem vorgegebenen Radius zurück.

Kreisfläche und Kreisumfang nach Archimedes:$A_{D}={\tfrac {1}{2}}U_{K}\cdot r=A_{K}$

„Jeder Kreis ist einem rechtwinkligen Dreiecke inhaltsgleich, insofern der Radius gleich der einen der den rechten Winkel einschließenden Seiten, der Umfang aber gleich der Basis [gemeint ist: der anderen Kathete] ist. “

–Archimedes:Die Kreismessung

In seiner AbhandlungDie Kreismessungkonnte Archimedes zeigen, dass der Umfang eines Kreises größer als3 ¹⁰⁄₇₁und kleiner als3 ¹⁄₇des Durchmessers ist. Für praktische Zwecke wird diese Näherung²²⁄₇(~ 3,143) heute noch verwendet.

Aus diesen beiden Aussagen folgert man, dass sich der Flächeninhalt eines Kreises zum Quadrat seines Durchmessers nahezu wie¹¹⁄₁₄verhält. Euklid war bereits bekannt, dass sich der Flächeninhalt eines Kreises proportional zum Quadrat seines Durchmessers verhält.Archimedes gibt hier eine gute Näherung der Proportionalitätskonstante an.

In einer weiteren ArbeitÜber Spiralenbeschreibt Archimedes die Konstruktion der später nach ihm benanntenarchimedischen Spirale.Mit dieser Konstruktion war es Archimedes möglich, den Umfang eines Kreises auf einer Geraden abzutragen. Auf diese Weise konnte nun der Flächeninhalt eines Kreises exakt bestimmt werden. Jedoch kann diese Spirale nicht mit Zirkel und Lineal konstruiert werden.

Apollonios von Pergelebte zirka 200 Jahre vor Christus. In seiner KegelschnittlehreKonikafasste er unter anderem dieEllipseund den Kreis als Schnitte eines geraden Kreiskegels auf – genauso wie es heute noch in deralgebraischen Geometriedefiniert wird. Seine Erkenntnisse gehen auf seine Vorgänger Euklid undAristaios(um 330 v. Chr.) zurück, deren verfasste Abhandlungen über Kegelschnitte jedoch nicht mehr überliefert sind.

Nach Apollonios ist weiterhin dasapollonische Problembenannt, zu drei gegebenen Kreisen mit den euklidischen Werkzeugen Lineal und Zirkel die Kreise zu konstruieren, die die gegebenen berühren. Jedoch im Vergleich zu Euklids Elementen, die auch im Mittelalter die Grundlage der Geometrie bildeten, fanden die Werke von Apollonios zunächst nur im islamischen Bereich Beachtung. In Westeuropa erlangten seine Bücher erst im 17. Jahrhundert größere Bedeutung, alsJohannes Keplerdie Ellipse als die wahre Bahn eines Planeten um die Sonne erkannte.

Renaissance

In der Wissenschaftsgeschichte nennt man den Zeitraum zwischen 1400 n. Chr. und 1630 n. Chr. üblicherweiseRenaissance,auch wenn der zeitliche Abschnitt nicht mit der Periodisierung etwa der Kunstgeschichte übereinstimmt. In dieser Zeit fanden EuklidsElementewieder mehr Beachtung. Sie gehörten zu den ersten gedruckten Büchern und wurden in den darauffolgenden Jahrhunderten in vielen verschiedenen Ausgaben verlegt.Erhard Ratdoltstellte 1482 in Venedig die erste gedruckte Ausgabe derElementeher. Eine der bedeutendsten Ausgaben von EuklidsElementenwurde von dem JesuitenChristoph Claviusherausgegeben. Er fügte den eigentlichen Texten Euklids neben den spätantiken Büchern XIV und XV noch ein sechzehntes Buch und weitere umfangreiche Ergänzungen hinzu. Beispielsweise ergänzte er eine Konstruktion der gemeinsamen Tangenten zweier Kreise.

19. Jahrhundert

Ferdinand von Lindemann

Nach Vorleistungen vonLeonhard Euler,der dieeulersche Identitätaufstellte,Johann Heinrich LambertundCharles HermitekonnteFerdinand von Lindemann1882 beweisen, dass die Zahl$\pi$transzendent ist. Das heißt, es gibt keinePolynomfunktionmitrationalenKoeffizienten, für die π eine Nullstelle ist. Da jedoch schon im 17. Jahrhundert gezeigt wurde, dass die Kreiszahl$\pi$eine Nullstelle einer solchen Polynomfunktion sein müsse, damit dieQuadratur des Kreisesmit Zirkel und Lineal funktioniere, wurde somit zugleich bewiesen, dass es kein solches Verfahren geben kann.

Gleichungen

In deranalytischen Geometriewerden geometrische Objekte mit Hilfe vonGleichungenbeschrieben. Punkte in der Ebene werden dazu meist durch ihrekartesischen Koordinaten$(x,y)$dargestellt und ein Kreis ist dann die Menge aller Punkte, deren Koordinaten die jeweilige Gleichung erfüllen.

Koordinatengleichung

Dereuklidische Abstandeines Punktes$\mathrm {X} =(x,y)$vom Punkt$\mathrm {M} =(x_{M},y_{M})$berechnet sich als

${\overline {\rm {XM}}}={\sqrt {(x-x_{M})^{2}+(y-y_{M})^{2}}}.$

Durch Quadrieren der definierenden Gleichung${\overline {\rm {XM}}}=r$ergibt sich die Koordinatengleichung

$\left(x-x_{M}\right)^{2}+\left(y-y_{M}\right)^{2}=r^{2}$

für die Punkte$(x,y)$auf dem Kreis mit Mittelpunkt$\mathrm {M} =(x_{M},y_{M})$und Radius$r$. Ausmultipliziert ergibt sich daraus:

$x^{2}+y^{2}+ax+by+c=0$

mit

$a=-2x_{M}$,$b=-2y_{M}$und$c=x_{M}^{2}+y_{M}^{2}-r^{2}$.

Ein wichtiger Spezialfall ist die Koordinatengleichung desEinheitskreises

$x^{2}+y^{2}=1.$

Funktionsgleichung

Da der Kreis keinFunktionsgraphist, lässt er sich auch nicht durch eineFunktionsgleichungdarstellen. Behelfsweise kann einPaarvon Funktionsgleichungen

$y=y_{M}\pm {\sqrt {r^{2}-(x-x_{M})^{2}}}$

verwendet werden. Für den Einheitskreis vereinfacht sich dieses zu

$y=\pm {\sqrt {1-x^{2}}}.$

Parameterdarstellung

Eine andere Möglichkeit, einen Kreis durch Koordinaten zu beschreiben, bietet die Parameterdarstellung (siehe auchPolarkoordinaten):

${\begin{aligned}x&=x_{M}+r\cos \varphi \\y&=y_{M}+r\sin \varphi \end{aligned}}$

Hier werden die Koordinaten$x$und$y$durch denParameter$\varphi$ausgedrückt, der alle Werte mit$0\leq \varphi <2\pi$annehmen kann.

Wendet man auch diese Gleichungen speziell auf den Einheitskreis an, so erhält man:

${\begin{aligned}x&=\cos \varphi \\y&=\sin \varphi \end{aligned}}$

Es ist auch eine Parameterdarstellung ohne den Rückgriff auf trigonometrische Funktion möglich(rationale Parametrisierung),allerdings wird dabei die gesamte Menge der reellen Zahlen als Parameterbereich benötigt und der Punkt$(x_{M}-r,y_{M})$wird nur als Grenzwert für$t\to \pm \infty$erreicht.

${\begin{aligned}x&=x_{M}+r{\frac {1-t^{2}}{1+t^{2}}}\\y&=y_{M}+r{\frac {2t}{1+t^{2}}}\end{aligned}}$

Für den Einheitskreis ergibt sich dann:

${\begin{aligned}x&={\frac {1-t^{2}}{1+t^{2}}}\\y&={\frac {2t}{1+t^{2}}}\end{aligned}}$

Komplexe Darstellung

In derkomplexen Zahlenebenelässt sich der Kreis um$m\in \mathbb {C}$mit Radius$r>0$durch die Gleichung

$|z-m|=r$

darstellen. Mit Hilfe der komplexenExponentialfunktionerhält man die Parameterdarstellung

$z=m+re^{i\varphi },\quad 0\leq \varphi <2\pi.$

Dreipunkteform einer Kreisgleichung

Die Koordinatengleichung des Kreises durch drei vorgegebene Punkte$(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$,die nicht auf einer Gerade liegen, ergibt sich durch Umformung der3-Punkteform(Beseitigung der Nenner und quadratische Ergänzung):

${\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}\;.$

Kreis durch drei Punkte

Aus der Dreipunkteform und der Koordinatengleichung ergibt sich für den Kreis durch drei vorgegebene Punkte$(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$mit

$z_{1}:={x_{1}}^{2}+{y_{1}}^{2},\quad z_{2}:={x_{2}}^{2}+{y_{2}}^{2},\quad z_{3}:={x_{3}}^{2}+{y_{3}}^{2}$

und den Determinanten

$A:=\det {\begin{pmatrix}1&1&1\\y_{1}&y_{2}&y_{3}\\z_{1}&z_{2}&z_{3}\end{pmatrix}},\quad B:=\det {\begin{pmatrix}x_{1}&x_{2}&x_{3}\\1&1&1\\z_{1}&z_{2}&z_{3}\end{pmatrix}},\quad C:=\det {\begin{pmatrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\1&1&1\end{pmatrix}},\quad D:=\det {\begin{pmatrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\z_{1}&z_{2}&z_{3}\end{pmatrix}}\quad$

für den Mittelpunkt$(x_{m},y_{m})$und den Radius$r\colon$

$x_{m}=-{\frac {A}{2C}},\quad y_{m}=-{\frac {B}{2C}};\quad r^{2}={\frac {A^{2}+B^{2}+4CD}{4C^{2}}}$

Liegen die drei gegebenen Punkte auf einer Geraden, so ist$C=0$.

Kreisberechnung

Kreiszahl

→Hauptartikel:Kreiszahl

Das Verhältnis von Kreisumfang zu Kreisdurchmesser ist aus Gründen derÄhnlichkeitfür alle Kreise gleich groß. Der Zahlenwert dieses Verhältnisses wird in der Elementargeometrie als die Kreiszahl

$\pi ={\frac {U}{d}}={\frac {U}{2r}}.$

definiert. Die Zahl$\pi$hat den Wert$\pi =3{,}14159\dots$.Sie ist einetranszendente Zahl,die auch in vielen anderen Bereichen der Mathematik eine herausragende Bedeutung hat.

Umfang

Entsprechend der obigen Definition von$\pi$als das Verhältnis von Kreisumfang$U$zu Kreisdurchmesser$d$gilt

$U=\pi d=2\pi r.$

Dabei ist$r$der Radius des Kreises.

Kreisfläche

Ein Vergleich des Flächeninhalts$A$einer Kreisscheibe mit einem Quadrat über seinem Radius verdeutlicht, dass$A$größer als$2r^{2}$und kleiner als$4r^{2}$ist.

Näherung der Kreisfläche durch ein Rechteck

DerFlächeninhalt$A$(lat.area:Fläche) der Kreisfläche, auch Kreisinhalt genannt, lässt sich durchGrenzwert-Betrachtungen berechnen, die aufArchimedeszurückgehen. Wenn man den Kreis, wie in der nebenstehenden Abbildung veranschaulicht, in Kreissektoren zerlegt, lässt sich seine Fläche in eine annähernd rechteckige Form (rechte Figur) bringen. Der Flächeninhalt bleibt gleich. Je feiner man nun den Kreis in Sektoren unterteilt, um so mehr nähert sich die nur annähernd rechteckige Form (rechte Figur) einem Rechteck an mit der Länge$\pi \,r$(halber Umfang) und der Breite$r$.Im Grenzwert ergibt sich als Flächeninhalt$A$der Kreisfläche somit:

$A=\pi r^{2}={\frac {\pi d^{2}}{4}}\approx 0{,}78540\;d^{2}.$

Ein formaler Beweis dieser Formel lässt sich zum Beispiel überIntegrierenderKreisgleichungführen oder nutzt, wie Archimedes, die unten beschriebeneAnnäherungdurch regelmäßige Vielecke.

Aus Gründen derÄhnlichkeitist der Flächeninhalt$A$der Kreisfläche proportional zum Quadrat desRadius$r$(und damit auch zum Quadrat desDurchmessers$d$) eines Kreises. Die Grenzwert-Betrachtung mittels der Zerlegung des Kreises in Sektoren (siehe Abbildung oben) zeigt, dass der Proportionalitätsfaktor identisch ist mit dem Proportionalitätsfaktor beim Verhältnis von Umfang und Durchmesser eines Kreises, also gleich$\pi$.

Durchmesser

→Hauptartikel:Durchmesser

Der Durchmesser$d$eines Kreises mit Flächeninhalt$A$und mit Radius$r$lässt sich durch

$d=2r=2{\sqrt {\frac {A}{\pi }}}\approx 1{,}12838\;{\sqrt {A}}$

berechnen.

Krümmung

Eine im Vergleich zu den bis jetzt beschriebenen Größen weniger elementare Eigenschaft des Kreises ist dieKrümmung.Zur präzisen Definition der Krümmung werden Begriffe aus derAnalysisbenötigt, sie lässt sich jedoch aufgrund der Symmetrieeigenschaften des Kreises einfach berechnen. Anschaulich gibt die Krümmung in jedem Punkt$\mathrm {P}$an, wie stark der Kreis in der unmittelbaren Umgebung des Punktes$\mathrm {P}$von einer Geraden abweicht. Die Krümmung$\kappa$des Kreises im Punkt$\mathrm {P}$lässt sich durch

$\kappa (\mathrm {P} )={\frac {1}{r}}$

berechnen, wobei$r$wieder der Radius des Kreises ist. Im Gegensatz zu anderen mathematischenKurvenhat der Kreis in jedem Punkt die gleiche Krümmung. Außer dem Kreis hat nur noch die Gerade eine konstante Krümmung, mit$\kappa =0$.Bei allen anderen Kurven ist die Krümmung vom Punkt$\mathrm {P}$abhängig.

Weitere Formeln

In den folgenden Formeln bezeichnet$\alpha$den Sektorwinkel imBogenmaß.Bezeichnet$\alpha '$den Winkel imGradmaß,so gilt die Umrechnung$\alpha ={\tfrac {\pi }{180^{\circ }}}\alpha '$.

Formeln zum Kreis
Fläche einesKreisringes	$A=\pi (r_{a}^{2}-r_{i}^{2})$
Länge eines Kreisbogens	$L_{B}=r\alpha$
FlächeKreissektor	$A_{\mathrm {SK} }={\frac {r^{2}}{2}}\alpha$
Fläche einesKreissegments	$A_{\mathrm {SG} }={\frac {r^{2}}{2}}\cdot \left(\alpha -\sin \alpha \right)$
LängeKreissehne	$l_{\mathrm {KS} }=2r\sin {\frac {\alpha }{2}}$
Höhe (Kreissegment)	$h=r-r\cos {\frac {\alpha }{2}}$

Näherungen für den Flächeninhalt

Da die Kreiszahl$\pi$einetranszendente Zahlist, gibt es kein Konstruktionsverfahren mit Zirkel und Lineal, mit dem man den Flächeninhalt exakt bestimmen kann. Außerdem sind transzendente Zahlen auchirrational,und daher hat$\pi$auch keineendliche Dezimalbruchentwicklung,weshalb der Kreisflächeninhalt beirationalemRadius auch keine endliche Dezimalbruchentwicklung besitzt. Aus diesen Gründen wurden bis heute unterschiedliche Näherungsverfahren für den Flächeninhalt und somit auch den Umfang eines Kreises entwickelt. Manche der Näherungsverfahren, wie beispielsweise das im AbschnittAnnäherung durch Vieleckeerläuterte Verfahren, können durch mehrfache Wiederholung ein beliebig genaues Ergebnis liefern.

Annäherung durch Quadrate

Ein Kreis mit Radius$r$wird mit einem Quadrat der Seitenlänge$2r$umschrieben. Ihm wird weiter ein Quadrat mit der Diagonalen$2r$einbeschrieben. Der Flächeninhalt des äußeren Quadrates ist$4r^{2}$,der des inneren nach derDreiecksflächenformel$2r^{2}$und derMittelwertist somit$3r^{2}$.Mit dieser Näherung$3r^{2}$wird die Kreisfläche mit einemrelativen Fehlervon weniger als 5 % bestimmt.

Auszählen in einem Raster

Die Kreisfläche lässt sich annähernd bestimmen, indem man ihr viele kleine Quadrate unterlegt (z. B. mitMillimeterpapier). Zählt man alle Quadrate, die vollständig innerhalb des Kreises liegen, so erhält man einen etwas zu niedrigen Wert für die Fläche, zählt man auch alle Quadrate mit, die den Kreis lediglich schneiden, so ist der Wert zu groß. Der Mittelwert beider Ergebnisse ergibt eine Näherung für den Flächeninhalt des Kreises, deren Güte mit der Feinheit des Quadratrasters steigt.

Annäherung durch Integration

Man kann die Fläche des Kreises aus im Verhältnis zum Radius sehr schmalen Streifenzusammensetzen.Dazu verwendet man die Gleichungen

$y=\pm {\sqrt {r^{2}-x^{2}}}$und$A_{K}=\pi r^{2}=\int _{-r}^{r}2{\sqrt {r^{2}-x^{2}}}\,\mathrm {d} x$.

Annäherung an den Umkreis über ein Sechseck und ein Zwölfeck

Kreisflächen-Integration

Annäherung durch Vielecke

Bei einer anderen Möglichkeit zur Kreisflächenbestimmung ist in den Kreis ein regelmäßigesSechseckeinzuzeichnen, dessen Ecken auf dem Kreis liegen. Werden nun die Seitenmitten vom Mittelpunkt aus auf den Kreis projiziert und diese neuen Punkte mit den alten Ecken verbunden, so entsteht ein regelmäßigesZwölfeck.Wird dieser Vorgang wiederholt, entstehen nacheinander ein 24-Eck, ein 48-Eck und so fort.

In jedem Sechseck sind die Seiten gleich lang wie der Umkreisradius. Die Seiten der folgenden Vielecke ergeben sich mit Hilfe desSatzes von Pythagorasjeweils aus den Seiten der vorhergehenden. Aus den Seiten lassen sich die Flächen der Vielecke durchDreiecksflächenberechnung exakt bestimmen. Sie sind alle etwas kleiner als die Kreisfläche, der sie sich bei steigender Eckenzahl jedoch annähern.

Entsprechend kann man mit einem Sechseck verfahren, das von außen an den Kreis gezeichnet ist, dessen Seitenmitten also auf ihm liegen. Man erhält eine fallendeFolgevon Flächenmaßen, derenGrenzwertwiederum die Kreisfläche ist.

Geometrische Sätze und Begriffe rund um den Kreis

Symmetrie und Abbildungseigenschaften

Der Kreis ist eine geometrische Figur von sehr hoherSymmetrie.Jede Gerade durch seinen Mittelpunkt ist eineSymmetrieachse.Zudem ist der Kreisrotationssymmetrisch,d. h., jedeDrehungum den Mittelpunkt bildet den Kreis auf sich selbst ab. In derGruppentheoriewerden die genannten Symmetrieeigenschaften des Kreises durch seineSymmetriegruppecharakterisiert. Formal ergibt sich dafür dieorthogonale Gruppe$\mathrm {O} (2)$,das ist dieGruppederorthogonalen$2\times 2$-Matrizen.

Alle Kreise mit dem gleichen Radius sind zueinanderkongruent,lassen sich also durchParallelverschiebungenaufeinander abbilden. Zwei beliebige Kreise sind zueinanderähnlich.Sie lassen sich stets durch einezentrische Streckungund eine Parallelverschiebung aufeinander abbilden.

Kreiswinkel und Winkelsätze

→Hauptartikel:KreiswinkelundSatz von Thales

Kreiswinkel: Der Umfangswinkel$\gamma$hängt nicht von der Lage des Punktes C auf dem Kreisbogen ab. Er ist halb so groß wie der Zentriwinkel$\varphi$und genauso groß wie der Sehnentangentenwinkel$\delta$.

Halbkreis mit rechtwinkligen Dreiecken

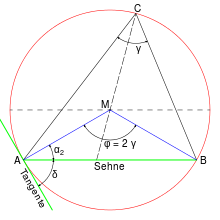
Eine Kreissehne mit Endpunkten A und B teilt einen gegebenen Kreis in zwei Kreisbögen. Ein Winkel$\angle {\rm {ACB}}$mit Scheitel C auf einem der Kreisbögen wirdUmfangswinkeloderPeripheriewinkelgenannt. Der Winkel$\angle {\rm {AMB}}$mit Scheitel im Mittelpunkt M heißtMittelpunktswinkeloderZentriwinkel.

Im Spezialfall, dass die Sehne den Mittelpunkt enthält, also ein Durchmesser des Kreises ist, ist der Mittelpunktswinkel ein gestreckter Winkel mit 180°. In dieser Situation gilt eine grundlegende Aussage der Kreisgeometrie, der Satz von Thales: Er besagt, dass Umfangswinkel über einem Durchmesser stets rechte Winkel sind, also 90° betragen. Der Kreis um dasrechtwinklige Dreieckwird in dieser Situation auchThaleskreisgenannt (Weiteres im AbschnittThaleskreis).

Auch im Fall einer beliebigen Kreissehne sind alle Umfangswinkel, die auf dem gleichen Kreisbogen liegen, gleich groß. Diese Aussage wird auchUmfangswinkelsatzgenannt. Der Kreisbogen, auf dem die Scheitel der Umfangswinkel liegen, heißtFasskreisbogen.Liegen Umfangswinkel und Zentriwinkel auf der gleichen Seite der Sehne, dann ist der Zentriwinkel doppelt so groß wie der Umfangswinkel(Kreiswinkelsatz).Zwei Umfangswinkel, die auf gegenüberliegenden Seiten der Sehne liegen, ergänzen einander zu 180°.

Der Umfangswinkel ist genauso groß wie der spitzeSehnentangentenwinkelzwischen der Sehne und der durch einen ihrer Endpunkte verlaufenden Tangente(Sehnentangentenwinkelsatz).

Sätze über Sehnen, Sekanten und Tangenten

Für Kreise gilt derSehnensatz,der besagt: Schneiden zwei Sehnen [AC] und [BD] einander in einem Punkt S, so gilt

${\overline {\rm {AS}}}\cdot {\overline {\rm {CS}}}={\overline {\rm {BS}}}\cdot {\overline {\rm {DS}}},$

d. h., die Produkte der jeweiligen Sehnenabschnitte sind gleich.

Zwei Sehnen eines Kreises, die einander nicht schneiden, können verlängert werden zu Sekanten, die entweder parallel sind oder einander in einem Punkt S außerhalb des Kreises schneiden. Ist Letzteres der Fall, so gilt analog zum Sehnensatz derSekantensatz

${\overline {\rm {AS}}}\cdot {\overline {\rm {CS}}}={\overline {\rm {BS}}}\cdot {\overline {\rm {DS}}}.$

Im Fall einer Sekante, die den Kreis in den Punkte A und C schneidet, und einer Tangente, die den Kreis im Punkt B berührt, gilt derSekanten-Tangenten-Satz:Ist S der Schnittpunkt von Sekante und Tangente, so folgt

${\overline {\rm {AS}}}\cdot {\overline {\rm {CS}}}={\overline {\rm {BS}}}^{2}.$

Umkreise und Inkreise in Dreiecken

Sind A, B, C drei Punkte, die nicht auf einer Geraden liegen, also ein nicht ausgeartetesDreieckbilden, dann existiert ein eindeutig bestimmter Kreis durch diese Punkte, nämlich derUmkreisdes Dreiecks ABC. Der Mittelpunkt des Umkreises ist der Schnittpunkt der dreiMittelsenkrechtendes Dreiecks. Ebenso kann jedem Dreieck ein eindeutig bestimmter Kreiseinbeschriebenwerden, der die drei Seiten berührt, d. h., die Dreiecksseiten bilden Tangenten des Kreises. Dieser Kreis wirdInkreisdes Dreiecks genannt. Sein Mittelpunkt ist der Schnittpunkt der dreiWinkelhalbierenden.

In der Elementargeometrie werden noch weitereKreise am Dreieckbetrachtet: DieAnkreiseliegen außerhalb des Dreiecks und berühren eine Seite und die Verlängerungen der beiden anderen Seiten. Ein weiterer interessanter Kreis am Dreieck ist derFeuerbachkreis,benannt nachKarl Wilhelm Feuerbach.Auf ihm liegen die drei Seitenmittelpunkte und die dreiFußpunktederHöhen.Da auf ihm außerdem die drei Mittelpunkte der Strecken zwischen dem Höhenschnittpunkt und den Ecken des Dreiecks liegen, wird der Feuerbachkreis auchNeunpunktekreisgenannt. Sein Mittelpunkt liegt wie derSchwerpunkt,der Umkreismittelpunkt und der Höhenschnittpunkt auf dereulerschen Geraden.

Umkreise in unregelmäßigen Vielecken

Im Gegensatz zu Dreiecken besitzen unregelmäßigePolygone(Vielecke) mit mehr als drei Ecken im Allgemeinen keinen Umkreis oder Inkreis. Fürregelmäßige Polygoneexistieren beide, eingezeichnet oder nicht, allerdings stets.

Viereck

EinViereck,das einen Umkreis besitzt, wirdSehnenviereckgenannt. EinkonvexesViereck ist genau dann ein Sehnenviereck, wenn sich gegenüberliegende Winkel zu 180° ergänzen. Ein Viereck, das einen Inkreis besitzt, wirdTangentenviereckgenannt. Ein konvexes Viereck ist genau dann ein Tangentenviereck, wenn die Summe der Seitenlängen zweier gegenüberliegender Seiten gleich der Summe der beiden anderen Seitenlängen ist.

Sechseck

Satz von Ceva für Kreise

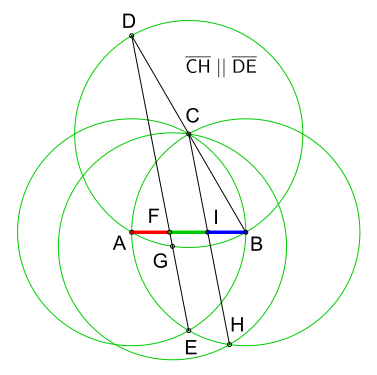
Ein unregelmäßiges Sechseck mit Umkreis (auchSehnensechseckgenannt), dessen Diagonalen sich in einem Punkt schneiden, hat besondere Eigenschaften, die an denSatz von Cevaerinnern. In der Fachliteratur wird der nachfolgende Satz deshalb mitunter auch als „Satz von Ceva für Kreise“bezeichnet:

In einem Kreis schneiden sich die drei Sehnen$AX$,$BY$und$CZ$in einem Punkt$P$(siehe Abbildung). Dann gilt für die Seiten des einbeschriebenen Sechsecks$AZBXCY$dieVerhältnisgleichung

${\frac {d}{e}}={\frac {f}{g}}={\frac {h}{k}}$.

Nach dem Sehnensatz sind folgende Dreiecke ähnlich zueinander:

$AZP$zu$XCP$,$BXP$zu$YAP$,$CYP$zu$ZBP$

Also gilt:

${\frac {d}{g}}={\frac {a}{x}}={\frac {z}{c}}$

${\frac {f}{k}}={\frac {b}{y}}={\frac {x}{a}}$

${\frac {h}{e}}={\frac {c}{z}}={\frac {y}{b}}$

Da die Flächeninhalte ähnlicher Figuren wie die Quadrate der entsprechenden Seitenlängen ansteigen, folgt

${\frac {d}{e}}\cdot {\frac {f}{g}}\cdot {\frac {h}{k}}={\frac {d}{g}}\cdot {\frac {f}{k}}\cdot {\frac {h}{e}}=\left({\frac {az}{cx}}\cdot {\frac {bx}{ay}}\cdot {\frac {cy}{bz}}\right)^{\frac {1}{2}}=1$

und weiter für die Flächeninhalte der Teildreiecke:

${\frac {[AZP]}{[XCP]}}={\frac {d^{2}}{g^{2}}}$

${\frac {[XPB]}{[PYA]}}={\frac {f^{2}}{k^{2}}}$

${\frac {[PCY]}{[ZBP]}}={\frac {h^{2}}{e^{2}}}$

Somit gilt:

${\frac {[AZP]\cdot [XPB]\cdot [PCY]}{[XCP]\cdot [PYA]\cdot [ZBP]}}=\left({\frac {d}{e}}\cdot {\frac {f}{g}}\cdot {\frac {h}{k}}\right)^{2}=1$

Daraus folgt

${\frac {d}{e}}={\frac {f}{g}}={\frac {h}{k}}$

und gleichzeitig, dass das Produkt der Flächen der grünen Dreiecke gleich dem Produkt der Flächen der gelben Dreiecke ist.

Damit ist die Aussage des Satzes bewiesen.

Einem Kreis einbeschriebene Kreise

→Hauptartikel:Dreipass,VierpassundVielpass

Beziehungen im Dreipass

Gegeben sei einDreipassmit drei sich paarweise berührendenkongruentenKreisen mit Radius$r$,die einem Kreis$k$mit Radius$R$einbeschrieben sind. Dann gilt

$r=R\cdot \left(2{\sqrt {3}}-3\right)$.

Beweis:

Figur 1

Der Umkreis einesgleichseitigen Dreiecksmit der Seitenlänge$s$hat den Radius

$R={\frac {s}{3}}{\sqrt {3}}$,

was gleichbedeutend ist mit

$s=R{\sqrt {3}}$.

Hieraus folgt nach dem Strahlensatz im gelben Dreieck vonFigur 1

$(R-r):R=(2r):\left(R{\sqrt {3}}\right)$

und weiter nach elementaren algebraischen Termumformungen

$r=R\cdot \left(2{\sqrt {3}}-3\right)$.

Beziehungen im Vierpass

Figur 2

Gegeben sei einVierpassaus Dreiviertelkreisbögen von vier kongruenten Kreisen mit Radius$r$,die einem Kreis$k$mit Radius$R$einbeschrieben sind. Dann gilt

$r=R\cdot \left({\sqrt {2}}-1\right)$.

Beweis:

Nach dem Satz des Pythagoras gilt im gelben Dreieck vonFigur 2

$(2r)^{2}=2\cdot \left(R-r\right)^{2}$.

Hieraus folgt nach elementaren algebraischen Termumformungen

$r=R\cdot \left({\sqrt {2}}-1\right)$.

Figur 3

Beziehungen im Sechspass

Gegeben sei einSechspassaus Zweidrittelkreisbögen von sechs kongruenten Kreisen mit Radius$r$,die einem Kreis mit Radius$R$einbeschrieben sind. Dann gilt

$r={\frac {R}{3}}$.

Der Beweis ergibt sich unmittelbar ausFigur 3aufgrund der Eigenschaften der eingezeichneten gleichseitigen Dreiecke.

Bogendreieck

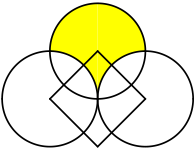
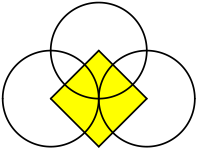
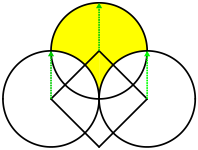
DreiEckpunkteeines Quadrats seien Mittelpunkte dreier Kreise, die durch den Diagonalenschnittpunkt des Quadrates verlaufen. Dann ist das Quadrat flächengleich zu dem von den drei Kreisen begrenzten gelben Bereich, dem sogenannten Bogendreieck(Figuren 4 und 5).

Der Beweis ergibt sich durch geometrische Verschiebungen und Drehungen aus denFiguren 6, 7 und 8.

Eine andere Beweisvariante verwendet eineParkettierungder Ebene mit den gelben Kreisteilen bzw. den rot umrandeten Quadraten. Die Flächengleichheit resultiert aus der Tatsache, dass einerseits die gelben Kreisteile und andererseits die rot umrandeten Quadrate jeweils die gesamte Ebene parkettieren(Figur 9).

Im Gegensatz zum Kreis ist es möglich, vom durch drei Kreisen begrenzten Bogendreieck ein flächengleiches Quadrat zu konstruieren.

• 
  Figur 4
• 
  Figur 5
• 
  Figur 6
• 
  Figur 7
• 
  Figur 8
• 
  Figur 9

Kreisspiegelungen und Möbiustransformationen

→Hauptartikel:KreisspiegelungundMöbiustransformation

Die Kreisspiegelung, auch Inversion genannt, ist eine spezielle Abbildung der ebenen Geometrie, die eine „Spiegelung “der euklidischen Ebene an einem gegebenen Kreis$k$mit Mittelpunkt${\rm {M}}$und Radius$r$beschreibt. Ist${\rm {P\neq M}}$ein gegebener Punkt, dann ist sein Bildpunkt${\rm {P'}}$dadurch bestimmt, dass er auf derHalbgeraden${\rm {MP}}$liegt und sein Abstand von${\rm {M}}$die Gleichung

${\overline {\rm {MP}}}\cdot {\overline {\rm {MP'}}}=r^{2}$

erfüllt. Die Kreisspiegelung bildet das Innere des gegebenen Kreises$k$auf sein Äußeres ab und umgekehrt. Alle Kreispunkte von$k$werden auf sich selbst abgebildet. Kreisspiegelungen sindwinkeltreu,orientierungsumkehrendundkreistreu.Letzteres bedeutet, dass verallgemeinerte Kreise – das sind Kreise und Geraden – wieder auf verallgemeinerte Kreise abgebildet werden.

Die Hintereinanderausführung zweier Kreisspiegelungen ergibt eine Möbiustransformation. Möbiustransformationen – eine weitere wichtige Klasse von Abbildungen der Ebene – sind daher ebenfalls winkeltreu und kreistreu, allerdings orientierungserhaltend.

Kreisspiegelungen und Möbiustransformationen lassen sich besonders übersichtlich mit Hilfe komplexer Zahlen darstellen: Bei einer Kreisspiegelung eines Punktes$z\in \mathbb {C} \setminus \{z_{0}\}$an dem Kreis$\{x\in \mathbb {C}:|x-z_{0}|=r\}$lautet die Formel für den Bildpunkt$w\in \mathbb {C} \setminus \{z_{0}\}$

$w=z_{0}+{\frac {r^{2}}{{\bar {z}}-{\bar {z}}_{0}}}.$

Für die Spiegelung am Einheitskreis gilt einfach$w=1/{\bar {z}}$.

Möbiustransformationen der komplexen Ebene werden durchgebrochen lineare Funktionender Gestalt

$w={\frac {az+b}{cz+d}}$

mit$a,b,c,d\in \mathbb {C}$und$ad\neq bc$dargestellt.

Siehe auch:Potenz (Geometrie)

Konstruktionen mit Zirkel und Lineal

In der Geometrie schlägt man Kreise mittels eines Zirkels.

Ein klassisches Problem derGeometrieist dieKonstruktion geometrischer Objekte mit Zirkel und Linealin endlich vielen Konstruktionsschritten aus einer gegebenen Punktemenge. In jedem Schritt dürfen dabei Geraden durch gegebene oder bereits konstruierte Punkte gezogen werden sowie Kreise um solche Punkte mit gegebenem oder bereits konstruiertem Radius gezogen werden. Die dadurch konstruierten Punkte ergeben sich als Schnittpunkte zweier Geraden, zweier Kreise oder einer Geraden mit einem Kreis. Naturgemäß spielen daher bei allen Konstruktionen mit Zirkel und Lineal Kreise eine wichtige Rolle.

Im Folgenden sollen exemplarisch einige Konstruktionen angesprochen werden, die im Zusammenhang mit der Geometrie von Kreisen von Bedeutung sind.

Thaleskreis

→Hauptartikel:Satz des Thales

Für die Konstruktion des Thaleskreises über einer gegebenen Strecke${\overline {\rm {AB}}}$wird zunächst der Mittelpunkt$\mathrm {M}$dieser Strecke konstruiert, der auch der Mittelpunkt des Thaleskreises ist. Dazu werden um$\mathrm {A}$und$\mathrm {B}$jeweils zwei kurze Kreisbögen mit dem gleichen Radius$r$geschlagen, wobei$r$so groß gewählt werden muss, dass die vier Kreisbögen sich in zwei Punkten$C$und$D$schneiden. Das ist z. B. für$r={\overline {\rm {AB}}}$der Fall. Die Strecke${\overline {\rm {CD}}}$schneidet dann${\overline {\rm {AB}}}$im Mittelpunkt$\mathrm {M}$.Der gesuchte Thaleskreis ist nun der Kreis mit Mittelpunkt$\mathrm {M}$und Radius${\overline {\rm {AM}}}={\overline {\rm {MB}}}$.(Figur 1)

• 
  Figur 1:Der Thaleskreis über einer gegebenen Strecke${\overline {\rm {AB}}}.$
  Tangenten mit Hilfe des Thaleskreises durchPunkt$\mathrm {P}$an den Kreis$k.$

Konstruktion von Tangenten

→Hauptartikel:Tangente

Gegeben sei ein Punkt$\mathrm {P}$außerhalb eines Kreises$k$mit Mittelpunkt$\mathrm {M}$und es sollen die beiden Tangenten an den Kreis konstruiert werden, die durch den Punkt$\mathrm {P}$laufen. Diese elementare Konstruktionsaufgabe lässt sich einfach mit Hilfe des Satzes von Thales lösen: Man konstruiert den Thaleskreis mit der Strecke${\overline {\rm {PM}}}$als Durchmesser. Die Schnittpunkte dieses Kreises mit$k$sind dann die Berührpunkte der gesuchten Tangenten. (Figur 1)

Kreis durch drei gegebene Punkte

Kreis (rot) verläuft durch die drei gegebenen Punkte$A,B$und$C$

Gegeben sind die Punkte$A,B$und$C$,gesucht ist jener Kreis der durch diese Punkte verläuft.

Es beginnt mit dem Ziehen dreier Kreise mit gleicher Zirkelöffnung mit dem Radius gleich dem zweitgrößten Abstand$|{\overline {AB}}|$um die Punkte$A,B$und$C$.Als Schnittpunkte ergeben sich$D,E,F$und$G$.Nun werden die beiden Mittelsenkrechten$ms_{1}$bzw.$ms_{2}$der Abstände$|{\overline {BC}}|$und$|{\overline {AB}}|$mithilfe der Verbindungen der Punkte$D$mit$E$und$F$mit$G$generiert. Schnittpunkt der beiden Mittelsenkrechten ist der Mittelpunkt$M$des gesuchten Kreises, der abschließend durch die drei Punkte$A,B$und$C$gezogen wird.

Streckendrittelung

Für jede der folgenden alternativen Figuren bedarf es nur einer Zirkelöffnung, sprich die Kreise haben stets denRadiusgleich der gegebenen Strecke${\overline {AB}}$.Die alphabetisch bezeichneten Punkte zeigen jeweils die Reihenfolge der Konstruktionsschritte für die Drittelung derStrecke${\overline {AB}}$an.

InFigur 2,Figur 4und inFigur 5erzeugt jeweils der Schnittpunkt$F$die Streckendrittelung.

InFigur 2ist die Strecke${\overline {AF}}$halb so lang wie die Strecke${\overline {FB}}$.

InFigur 3liefert der Teilungspunkt$T$die Drittelung der Strecke${\overline {AB}}$.

Konstruktion derSchnittpunkteinFigur 4bzw. inFigur 5:

• $F$ist der Schnittpunkt der Strecke${\overline {AB}}$und der Strecke${\overline {DE}}$.
• $G$ist der Schnittpunkt des Kreises mit dem Mittelpunkt$C$und der Strecke${\overline {DE}}$.
• $H$ist der Schnittpunkt des Kreises mit dem Mittelpunkt$B$und dem Kreis mit dem Mittelpunkt$G$.
• $I$ist der Schnittpunkt der Strecke${\overline {AB}}$und der Strecke${\overline {CH}}$und liefert somit das letzte Drittel der Strecke${\overline {AB}}$.

DieFigur 4mit den Kreismittelpunkten$A,B$und$C$undFigur 5mit den Kreismittelpunkten$A,B,C$und$G$sind elementare Vereinfachungen der Konstruktionen „Zwei Mal halbieren “bzw. „Drei Mal halbieren “von Hans Walser aus dem Jahr 2007.

• 
  Figur 2:Drittelung der Strecke${\overline {AB}}$
• 
  Figur 3:Drittelung der Strecke${\overline {AB}}$
  ${\overline {AT}}={\tfrac {1}{3}}{\overline {AB}}$
• 
  Figur 4:Streckendrittelung
  ${\overline {AF}}={\tfrac {1}{3}}{\overline {AB}}$
• 
  Figur 5:Strecke${\overline {AB}}$gedrittelt
  ${\overline {AF}}={\overline {FI}}={\overline {IB}}$

Flächenverdoppelung

Figur 6:Die Fläche des roten Kreises ist doppelt so groß wie die Fläche des kleinen, blauen Kreises.

Die Fläche eines Kreises lässt sich geometrisch verdoppeln, indem ein Quadrat gezeichnet wird, dessen eine Ecke im Kreismittelpunkt liegt, wobei zwei weitere Ecken auf dem Kreisbogen liegen. Durch die vierte Ecke wird ein Kreis um den alten Mittelpunkt gezogen. Dieses Verfahren wurde im 13. Jahrhundert im Bauhüttenbuch desVillard de Honnecourtdargestellt. Dieses Verfahren funktioniert, da (nach demSatz des Pythagoras)

$R^{2}=r^{2}+r^{2}=2r^{2}$

und damit der Flächeninhalt des großen Kreises

$\pi R^{2}=2\pi r^{2}$

genau doppelt so groß ist wie der des kleinen Kreises. (Figur 6)

Kreisteilung

→Hauptartikel:Kreisteilung

Ein weiteres bereits in der Antike untersuchtes Konstruktionsproblem ist die Kreisteilung. Hierbei soll zu einer gegebenennatürlichen Zahl$n$einem gegebenen Kreis ein regelmäßiges$n$-Eckeinbeschrieben werden. Die auf dem Kreis gelegenen Eckpunkte teilen diesen dann in$n$gleich lange Kreisbögen. Diese Konstruktion ist nicht für alle$n$möglich: Mit Hilfe deralgebraischenTheorie derKörpererweiterungenlässt sich zeigen, dass sie genau dann durchführbar ist, wenn$n$einePrimfaktorzerlegungder Form

$n=2^{k}\cdot p_{1}\dotsm p_{m}$

hat mit$k\in \mathbb {N} _{0}$und paarweise verschiedenenfermatschen Primzahlen$p_{1},\dots,p_{m}$,also Primzahlen der Form$2^{2^{r}}+1$. Damit ist die Konstruktion also beispielsweise für$n=3,4,5,6,8,10,12,15,16,17$möglich, jedoch nicht für z. B.$n=7,9,11,13,14$.Carl Friedrich Gaußwies im Jahre 1796 nach, dass die Konstruktion des regelmäßigenSiebzehnecksunter alleiniger Verwendung vonZirkel und Linealmöglich ist.

Konstruktionen nur mit dem Zirkel

→Hauptartikel:Satz von Mohr-Mascheroni

Bei gewissen geometrischen Konstruktionen kann auf ein Lineal verzichtet werden. DerfranzösischeKaiserNapoleon Bonaparte,der sich unter anderem auch mitgeometrischenFragestellungen befasste, lieferte zwei Beispiele für solcheKonstruktionsaufgaben,die in der Fachliteratur auch alsNapoleonische Problemebezeichnet werden.

Erstes Napoleonisches Problem

Sind ein Kreis$k$mit demMittelpunkt$M$und dem Radius$r$sowie ein Punkt$P$auf der Kreislinie gegeben, so sind die Eckpunkte eines einbeschriebenenQuadratsausschließlich mit demZirkelkonstruierbar.

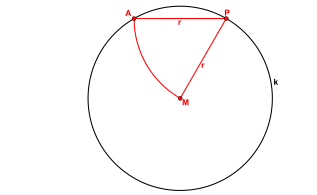
1. Konstruktionsschritt:

Zeichne einen Kreis um$P$mit dem Radius$r$.Der eineSchnittpunktdieses Kreises mit$k$sei$A$(von$P$aus gegen denUhrzeigersinn).

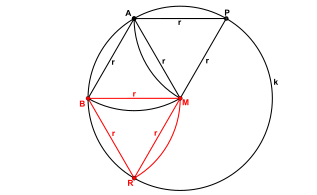
2. Konstruktionsschritt:

Zeichne einen Kreis um$A$mit dem Radius$r$.Der eine Schnittpunkt dieses Kreises mit$k$sei$B$(von$A$aus gegen den Uhrzeigersinn).

3. Konstruktionsschritt:

Zeichne einen Kreis um$B$mit dem Radius$r$.Der eine Schnittpunkt dieses Kreises mit$k$sei$R$(von$B$aus gegen den Uhrzeigersinn).

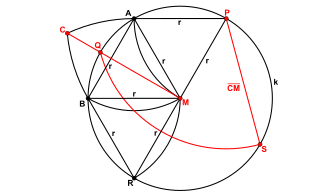
4. Konstruktionsschritt:

Zeichne einen Kreis um$P$durch$B$und einen Kreis um$R$durch$A$.Der eine Schnittpunkt dieser beiden Kreise sei$C$($C$liege außerhalb von$k$).

5. Konstruktionsschritt:

Zeichne einen Kreis um$P$mit dem Radius${\overline {CM}}$.Die Schnittpunkte dieses Kreises mit$k$seien$Q$und$S$.

Hierbei resultiert die Wahl des Radius${\overline {CM}}$aus folgendem Sachverhalt:

Das Dreieck$CMP$hat den rechten Winkel$\angle PMC$.Dieser setzt sich zusammen aus dem 60°-Winkel$\angle PMA$des gleichseitigen Dreiecks$AMP$und dem 30°-Winkel$\angle AMC$des durch$CM$symmetrischgeteilten gleichseitigen Dreiecks$ABM$.

Deshalb gilt nach demSatz des Pythagoras:

${\overline {MC}}^{2}+{\overline {MP}}^{2}={\overline {PC}}^{2}$

$PB$– und damit auch$PC$– ist doppelt so lang wie die Höhe${\frac {r}{2}}\cdot {\sqrt {3}}$des gleichseitigen Dreiecks$AMP$,bzw.$ABM$.

${\overline {MC}}^{2}={\overline {PC}}^{2}-{\overline {MP}}^{2}=3r^{2}-r^{2}=2r^{2}$

${\overline {MC}}=r\cdot {\sqrt {2}}$

Dies ist dieDiagonalenlängedes einbeschriebenen Quadrats$PQRS$.

Damit sind die Eckpunkte des einbeschriebenen Quadrats$PQRS$ausschließlich mit dem Zirkel konstruiert.

Grafische Darstellung der Konstruktionsschritte (Die hinzugekommenen Schritte sind jeweils rot markiert.):

• 
  Schritt 1
• 
  Schritt 2
• 
  Schritt 3
• 
  Schritt 4
• 
  Schritt 5
• 
  Fertige Konstruktion

Zweites Napoleonisches Problem

Sind ein Kreis$k$mit dem Radius$r$sowie ein Punkt$P$auf der Kreislinie gegeben, so ist der Mittelpunkt von$k$ausschließlich mit dem Zirkel konstruierbar.

1. Konstruktionsschritt:

Zeichne einen Kreis$h$um$P$mit einem Radius zwischen$r$und$2r$.Die Schnittpunkte von$h$und$k$seien$A$und$B$.

2. Konstruktionsschritt:

Zeichne einen Kreis um$A$mit dem Radius${\overline {AP}}$und einen Kreis um$B$mit dem Radius${\overline {BP}}$.Der zweite Schnittpunkt dieser beiden Kreise sei$C$.

3. Konstruktionsschritt:

Zeichne einen Kreis$c$um$C$mit dem Radius${\overline {CP}}$.Die Schnittpunkte von$c$und$h$seien$D$und$E$.

4. Konstruktionsschritt:

Zeichne einen Kreis um$D$mit dem Radius${\overline {DP}}$und einen Kreis um$E$mit dem Radius${\overline {EP}}$.Der zweite Schnittpunkt dieser beiden Kreise ist der Mittelpunkt$M$von$k$.

Grafische Darstellung der Konstruktionsschritte (Die hinzugekommenen Schritte sind jeweils rot markiert.):

• 
  Schritt 1
• 
  Schritt 2
• 
  Schritt 3
• 
  Fertige Konstruktion

Kreisberechnung in der Analysis

In der modernenAnalysiswerden dietrigonometrischen Funktionenund die Kreiszahl$\pi$üblicherweise zunächst ohne Rückgriff auf die elementargeometrische Anschauung und auf spezielle Eigenschaften des Kreises definiert. So lassen sich etwaSinus und Kosinusüber ihre Darstellung alsPotenzreihedefinieren. Eine gängige Definition für den Wert von$\pi$ist dann das Doppelte der kleinsten positiven Nullstelle des Kosinus.

Der Kreis als Kurve

In derDifferentialgeometrie,einem Teilgebiet der Analysis, das geometrische Formen mit Hilfe derDifferential-undIntegralrechnunguntersucht, werden Kreise als spezielleKurvenangesehen. Diese Kurven lassen sich mit Hilfe der oben genanntenParameterdarstellungalsWegbeschreiben. Legt man den Koordinatenursprung in den Mittelpunkt eines Kreises mit Radius$r$,dann ist durch die Funktion$f\colon [0,2\pi ]\to \mathbb {R} ^{2}$mit

$f(t)={\begin{pmatrix}r\cos t\\r\sin t\end{pmatrix}}$

eine solche Parametrisierung gegeben. Mit Hilfe dertrigonometrischen Formel$\sin ^{2}t+\cos ^{2}t=1$folgt für dieeuklidische Normder parametrisierten Punkte$|f(t)|=r$,das heißt, sie liegen tatsächlich auf einem Kreis mit Radius$r$. Da Sinus und Kosinus$2\pi$-periodischeFunktionen sind, entspricht das Definitionsintervall$[0,2\pi ]$von$f$genau einem Kreisumlauf.

Kreisumfang

Der Umfang des Kreises ergibt sich alsLängedes Weges$f$durchIntegrationzu

$U=L(f)=\int _{0}^{2\pi }|f'(t)|\,dt=\int _{0}^{2\pi }\left|{\begin{pmatrix}-r\sin t\\r\cos t\end{pmatrix}}\right|\,dt=\int _{0}^{2\pi }{\sqrt {r^{2}\sin ^{2}t+r^{2}\cos ^{2}t}}\,dt=r\int _{0}^{2\pi }1\,dt=2\pi r.$

Analog gilt für die Länge$s(t)$des durch$f|_{[0,t]}$gegebenen Teilkreisbogens$s(t)=rt$.Dadurch erhält man als Parametrisierung des Kreises nach der Bogenlänge

${\hat {f}}(s)={\begin{pmatrix}r\cos(s/r)\\r\sin(s/r)\end{pmatrix}}$

mit$s\in [0,2\pi r]$.

Flächeninhalt

Der Flächeninhalt$A$der Kreisscheibe$K=\{(x,y)\in \mathbb {R} ^{2}:x^{2}+y^{2}\leq r^{2}\}$,also dasMaßder Menge$K$,kann als (zweidimensionales) Integral

$A=\int _{K}1\,d(x,y)$

dargestellt werden. Um die etwas mühsame Berechnung dieses Integrals in kartesischen Koordinaten zu umgehen, ist es günstig, eineTransformation$x=\rho \cos \varphi$,$y=\rho \sin \varphi$aufPolarkoordinatendurchzuführen. Damit ergibt sich

$A=\int _{0}^{2\pi }\int _{0}^{r}\rho \,d\rho \,d\varphi =\int _{0}^{r}\rho \,d\rho \cdot \int _{0}^{2\pi }d\varphi ={\frac {1}{2}}r^{2}\cdot 2\pi =\pi r^{2}.$

Eine andere Möglichkeit zur Berechnung der Kreisfläche besteht darin, dieSektorformel von Leibnizauf die Parameterdarstellung des Kreisrandes anzuwenden. Mit$x(t)=r\cos t$,$y(t)=r\sin t$erhält man damit ebenfalls

$A={\frac {1}{2}}\int _{0}^{2\pi }x(t)y'(t)-x'(t)y(t)\,dt={\frac {1}{2}}\int _{0}^{2\pi }r^{2}\cos ^{2}t+r^{2}\sin ^{2}t\,dt={\frac {1}{2}}r^{2}\int _{0}^{2\pi }dt=\pi r^{2}.$

Krümmung

Für die oben hergeleitete Parametrisierung${\hat {f}}(s)$des Kreises nach seiner Bogenlänge ergibt sich

${\hat {f}}'(s)={\begin{pmatrix}-\sin {\frac {s}{r}}\\\cos {\frac {s}{r}}\end{pmatrix}}\quad {\text{und}}\quad {\hat {f}}''(s)={\begin{pmatrix}-{\frac {1}{r}}\cos {\frac {s}{r}}\\-{\frac {1}{r}}\sin {\frac {s}{r}}\end{pmatrix}}.$

Für dieKrümmungdes Kreises erhält man daher

$\kappa =|{\hat {f}}''(s)|={\sqrt {{\frac {1}{r^{2}}}\cos ^{2}{\frac {s}{r}}+{\frac {1}{r^{2}}}\sin ^{2}{\frac {s}{r}}}}={\frac {1}{r}}.$

Die Krümmung des Kreises ist also konstant und der Krümmungsradius${\tfrac {1}{\kappa }}=r$ist gerade sein Radius.

In der Differentialgeometrie wird gezeigt, dass eine ebene Kurve bis auf Kongruenz durch ihre Krümmung eindeutig bestimmt ist. Die einzigen ebenen Kurven mit konstanter positiver Krümmung sind daher Kreisbögen. Im Grenzfall, dass die Krümmung konstant gleich 0 ist, ergeben sich Geradenstücke.

Isoperimetrisches Problem

→Hauptartikel:Isoperimetrisches Problem

Unter allen Flächen der euklidischen Ebene mit gegebenem Umfang besitzt die Kreisfläche den größten Flächeninhalt. Umgekehrt hat die Kreisfläche bei gegebenem Flächeninhalt den kleinsten Umfang. In der Ebene ist der Kreis daher die eindeutig bestimmte Lösung des sog. isoperimetrischen Problems. Obwohl diese anschaulich einleuchtende Tatsache schon den Mathematikern im antiken Griechenland bekannt war, wurden formale Beweise erst im 19. Jahrhundert erbracht. Da eine Kurve gesucht ist, die einFunktionalmaximiert, nämlich den umschlossenen Flächeninhalt, handelt es sich dabei aus moderner Sicht um ein Problem derVariationsrechnung.Ein gängiger Beweis für stückweise stetige Kurven verwendet die Theorie derFourierreihen.

Verallgemeinerungen und verwandte Themen

Sphäre

→Hauptartikel:Sphäre (Mathematik)

Es ist möglich, den Kreis als Objekt der Ebene in den dreidimensionalen Raum zu verallgemeinern. Dann erhält man die Hülle einerKugel.Dieses Objekt wird in der Mathematik Sphäre oder genauer 2-Sphäre genannt. Analog lässt sich die 2-Sphäre auf$n$Dimensionen zur$n$-Sphäreverallgemeinern. In diesem Kontext nennt man den Kreis auch 1-Sphäre.

Kegelschnitte

→Hauptartikel:Kegelschnitt

Der Kreis als Kegelschnitt

In derebenen Geometriekann der Kreis als spezielleEllipseaufgefasst werden, bei der die beidenBrennpunktemit dem Kreismittelpunkt zusammenfallen. BeideHalbachsensind dabei gleich dem Kreisradius. Der Kreis ist daher ein spezieller Kegelschnitt: Er entsteht als Schnitt eines geraden Kreiskegelsmit einer Ebene senkrecht zu Kegelachse. Er ist damit ein Spezialfall einer zweidimensionalenQuadrik.

Hierbei ergibt sich eine weitere, äquivalente Definition für Kreise (Kreis des Apollonios): Ein Kreis ist die Menge aller Punkte in der Ebene, für die der Quotient$q$ihrer Abstände von zwei gegebenen Punkten konstant ist. Die beiden Punkte liegen auf einem von$M$ausgehendenStrahlim Abstand$r/q$bzw.$r\cdot q$und wechselseitig auf derPolarendes jeweils anderen Punktes als Pol. Ähnliche Definitionen gibt es auch für die Ellipse (konstante Summe),Hyperbel(konstante Differenz) und dieCassinische Kurve(konstantes Produkt der Abstände).

Kreise in der synthetischen Geometrie

In dersynthetischen Geometriekönnen Kreise in bestimmtenaffinen Ebenen(zum Beispielpräeuklidischen Ebenen) ohne einen Abstandsbegriff allein durch eineOrthogonalitätsrelationdefiniert werden, indem der Satz vomUmkreis(Mittellotensatz) zur Definition des Kreises verwendet wird. Dadurch kann dann ein schwächerer Begriff der „Abstands- “oder „Längengleichheit “vonPunktepaaren$(A,B)$in solchen Ebenen eingeführt werden. → Siehe dazuPräeuklidische Ebene.

Zeichnung im digitalen Raster

Für das Zeichnen von angenäherten Kreisen in einem Punktraster wurden mehrereAlgorithmenentwickelt, siehe dazuRasterung von Kreisen.Diese Verfahren sind insbesondere für dieComputergrafikvon Belang. Für die zweifarbige Rasterung von Kreisen reichen dieGrundrechenartenaus.

Siehe auch

• Einheitskreis
• Großkreis
• Halbkreis
• Kleinkreis
• Kreisbogen
• Kreisgruppe
• Kreisring
• Kreissegment
• Kreissektor
• Kreiswinkel
• Malfatti-Kreis
• Sehne (Geometrie)
• Zindlerkurve

Literatur

• Günter Aumann:Kreisgeometrie. Eine elementare Einführung.Springer, Berlin 2015,ISBN 3-662-45305-3.
• Ilka Agricola,Thomas Friedrich:Elementargeometrie.3. Auflage. Vieweg+Teubner, Wiesbaden 2011,ISBN 978-3-8348-1385-5.
• Christian Bär:Elementare Differentialgeometrie.2. Auflage. Walter de Gruyter, Berlin 2010,ISBN 978-3-11-022458-0.
• Hartmut Wellstein, Peter Kirsche:Elementargeometrie. Eine aufgabenorientierte Einführung.Vieweg+Teubner, Wiesbaden 2009,ISBN 978-3-8348-0856-1.
• Gyula Strommer:Konstruktionen allein mit dem Zirkel in der hyperbolischen Ebene.Journal für die reine und angewandte Mathematik (Crelles Journal), vol. 1964, no. 214–215, 1964, pp. 192–200
• Ludwig Bieberbach:Theorie der geometrischen Konstruktionen,Springer Basel 1952,ISBN 978-3-0348-6911-9

Weblinks

Commons:Kreis– Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Beweis der Transzendenz von e und π– im Beweisarchiv

Wiktionary: Kreis– Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Kreis.In: „Mathematische Basteleien “
• Eric W. Weisstein:Circle.In:MathWorld(englisch).

Wiktionary: Quadratur– Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen