Logistische Gleichung

Dielogistische Gleichungwurde ursprünglich 1837 vonPierre François Verhulstalsdemographischesmathematisches Modelleingeführt. Die Gleichung ist ein Beispiel dafür, wie komplexes,chaotischesVerhalten aus einfachen nichtlinearen Gleichungen entstehen kann. Infolge einer richtungsweisenden Arbeit destheoretischen BiologenRobert Mayaus dem Jahr 1976fand sie weite Verbreitung. Bereits 1825 stellteBenjamin Gompertzin einem verwandten Zusammenhang eine ähnliche Gleichung vor.

Die zugehörige Dynamik kann anhand eines sogenanntenFeigenbaumdiagramms(siehe unten) veranschaulicht werden. Eine wichtige Rolle spielt dabei die schon 1975 vonMitchell FeigenbaumgefundeneFeigenbaum-Konstante.

Das demographische Modell

Für den stetigen Fall siehelogistische Funktion.

Es werden mathematische Gesetzmäßigkeiten gesucht, die die Entwicklung einerPopulationmodellhaft darstellen. Aus der Größe$X_{n}$der Population zu einem gewissen Zeitpunkt$n$soll auf die Größe$X_{n+1}$nach einer Fortpflanzungsperiode (z. B. nach einem Jahr) geschlossen werden.

Das logistische Modell berücksichtigt zwei Einflüsse:

1. DurchFortpflanzungvermehrt sich die Populationgeometrisch.Die Individuenzahl ist im Folgejahr um einenWachstumsfaktor$q_{\mathrm {f} }$größer als die aktuelle Population.
2. DurchVerhungernverringert sich die Population. Die Individuenzahl vermindert sich in Abhängigkeit von derDifferenzzwischen ihrer aktuellen Größe und einer theoretischen Maximalgröße$G$mit derProportionalitätskonstante$q_{\mathrm {v} }$.Der Faktor, um den sich die Population vermindert, hat also die Gestalt$q_{\mathrm {h} }=(G-X_{n})\,q_{\mathrm {v} }$.

Um bei der Berechnung der Population im Folgejahr beide Prozesse zu berücksichtigen, multipliziert man die aktuelle Population$X_{n}$sowohl mit dem Vermehrungsfaktor$q_{\mathrm {f} }$als auch mit dem Hungerfaktor$q_{\mathrm {h} }$.Man erhält damit die logistische Gleichung

$X_{n+1}=q_{\mathrm {f} }\,q_{\mathrm {v} }\,X_{n}\,(G-X_{n})$.

Um die folgenden mathematischen Untersuchungen zu vereinfachen, wird die Populationsgröße$X_{n}$oft als Bruchteil$x_{n}$der Maximalgröße$G$angegeben:

$x_{n}={\frac {X_{n}}{G}}$.

Außerdem werden$G$,$q_{\mathrm {f} }$und$q_{\mathrm {v} }$zusammengefasst zum Parameter$r$:

$r=G\,q_{\mathrm {f} }\,q_{\mathrm {v} }$.

Damit ergibt sich die folgende Schreibweise für die logistische Gleichung:

$x_{n+1}=r\,x_{n}\,(1-x_{n}/K)$.

Hierbei ist$K$die Kapazität des Biotops. Das heißt, es ist die Population, die bei geeigneter Wahl von$r$dem Fixpunkt der Dynamik entspricht.

Das mathematische Modell

Man kann ohne Beschränkung der Allgemeinheit$K=1$setzen. Dann ergibt sich

$x_{n+1}=r\cdot x_{n}\cdot (1-x_{n})$.

$x_{n}$ist dabei eine Zahl zwischen$0$und$1$.Sie repräsentiert die relative Größe der Population im Jahr$n$.Die Zahl$x_{0}$steht also für die Startpopulation (im Jahr 0). Der Parameter$r$ist immer positiv, er gibt die kombinierte Auswirkung von Vermehrung und Verhungern wieder.

Verhalten in Abhängigkeit vonr

Die Animation unten zeigt Zeitreihenentwicklungen der Logistischen Gleichung im Zeit- und Frequenzbereich (Fourier-Analysis), die sich für wachsende Parameter$2<r<4$ergeben. Startwert ist jedes Mal$x_{0}={\tfrac {1}{2}}$.

Gut sichtbar sind die Zonen derIntermittenzinnerhalb desdeterministischen Chaos.

Bei verschiedenen$r$können die folgenden Verhaltensweisen für große$n$beobachtet werden. Dabei hängt dieses Verhalten nicht vom Anfangswert ab, sondern nur von$r$:

• Mit$r$von 0 bis 1 stirbt die Population in jedem Fall aus.
• Mit$r$zwischen 1 und 2 nähert sich die Population monoton demGrenzwert${\tfrac {r-1}{r}}$an.
• Mit$r$zwischen 2 und 3 nähert sich die Population dem Grenzwert${\tfrac {r-1}{r}}$alternierend, d. h. die Werte liegen ab einem bestimmten$n$abwechselnd über und unter dem Grenzwert.
• Mit$r$zwischen 3 und$1+{\sqrt {6}}$(etwa 3,45) wechselt die Folge bei fast allen Startwerten (ausgenommen 0, 1 und$1-{\tfrac {1}{r}}$) zwischen den beiden Umgebungen zweierHäufungspunkte.
• Mit$r$zwischen$1+{\sqrt {6}}$und ungefähr 3,54 wechselt die Folge bei fast allen Startwerten zwischen den Umgebungen von vier Häufungspunkten.
• Wird$r$größer als 3,54, stellen sich erst 8, dann 16, 32 usw. Häufungspunkte ein. Die Intervalle mit gleicher Anzahl von Häufungspunkten (Bifurkationsintervalle) werden immer kleiner; das Längenverhältnis zweier aufeinanderfolgender Bifurkationsintervalle nähert sich derFeigenbaumkonstanten.Diese Konstante ist auch in anderen mathematischen Zusammenhängen von Bedeutung. (Zahlenwert: δ ≈ 4,6692016091029906718532038204662016172581…).
• Bei$r$annähernd 3,57 beginnt dasChaos:Die Folge springt zunächst periodisch zwischen den Umgebungen der nun instabilen Häufungspunkte umher. Mit weiter wachsendem$r$verschmelzen diese Intervalle so, dass sich deren Anzahl im Rhythmus der Feigenbaumkonstante halbiert, bis es nur noch ein Intervall gibt, in dem die Folge chaotisch ist. Perioden sind dann nicht mehr erkennbar. Winzige Änderungen des Anfangswertes resultieren in unterschiedlichsten Folgewerten – eine Eigenschaft des Chaos.
• Bei vielen Koeffizienten zwischen 3,57 und 4 kommt es zu chaotischem Verhalten, obwohl für bestimmte$r$wieder Häufungspunkte (d. h. stabile periodische Orbits, gegen die fast jeder Anfangswert konvergiert) vorhanden sind. Beispielsweise existieren in der Nähe von$r=3{,}82$bei steigendem$r$erst 3, dann 6, 12 usw. Häufungspunkte. Ebenso gibt esr-Werte mit 5 oder mehr Häufungspunkten – alle Periodendauern tauchen auf.
• Drei tiefliegende mathematische Sätze besagen folgendes: (1) jedes noch so kleine Intervall von Koeffizienten enthält Parameter, für die es stabile periodische Orbits gibt (so dass die Dynamik eben nicht chaotisch ist): also nicht-chaotische Parameter sind "dicht" im Intervall der Koeffizienten. Chaotische Parameter enthalten also keine Intervalle. Aber (2) die chaotischen Parameter haben positives Maß: also mit echt positiver Wahrscheinlichkeit liefert ein zufälliger Parameter chaotische Dynamik. Schließlich (3) hat fast jeder reelle Koeffizient$r$(im Sinne voller Wahrscheinlichkeit) entweder einen stabilen periodischen Orbit (gegen den fast jeder Anfangswert konvergiert) oder ist in strengem Sinne "chaotisch". (Weitere dynamische Möglichkeiten gibt es, haben aber Wahrscheinlichkeit null.)
• Für$r$größer 4 divergiert die Folge für fast alle Anfangswerte und verlässt das Intervall$[0;1]$.

Dieser Übergang von konvergentem Verhalten über Periodenverdopplungen zu chaotischem Verhalten ist generell fürnichtlineare Systemetypisch, die in Abhängigkeit von einem Parameter chaotisches oder nicht-chaotisches Verhalten zeigen.

Eine Erweiterung des Wertebereiches auf diekomplexen Zahlenführt nach einerKoordinatentransformationzurMandelbrotmenge.

Beispiel

Die „logistische Kurve “mit einer Wachstumsrate$r=1{,}4$verläuft S-förmig. Ab einem Wert um 3,6 brichtChaosaus, wie die Abbildung mit$r=3{,}81$illustriert.

„Logistische Kurve “mit einer Wachstumsrater= 1,4

„Logistische Kurve “mit einer Wachstumsrater= 3,81

Graphische Darstellung

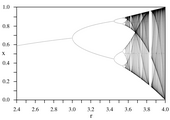
Das folgendeBifurkationsdiagramm,bekannt alsFeigenbaum-Diagramm,fasst diese Beobachtungen zusammen. Die horizontale Achse gibt den Wert des Parameters$r$an und die vertikale Achse die Häufungspunkte für die Folge$x_{n}$.

• 
  Bifurkationsdiagramm der logistischen Gleichung
• 
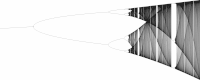
  Hochauflösende Version ohne Skala
• 
  Hochauflösender Ausschnitt des Bifurkationsdiagramms der logistischen Gleichung

• 
  Zusammenhang mit derMandelbrotmenge(nach Koordinatentransformation)

Analytische Lösung

Für den Parameter$r=2$existiert eine analytische Lösung:

$x(n)={\frac {1}{2}}-{\frac {1}{2}}(1-2x_{0})^{\left(2^{n}\right)}$.

Für die Parameter$r=-2$und$r=4$können ebenfalls analytische Lösungen angegeben werden.

Weblinks

• Eric W. Weisstein. "Feigenbaum Constant." From MathWorld--A Wolfram Web Resource.
• Analytische Lösung für die Parameter -2, 2, 4
• Online Berechnung des Bifurkationsdiagramms