Ortsvektor

Zwei Punkte und ihre Ortsvektoren

Ortsvektoren (hier durch${\vec {r}}_{P}$und${\vec {r}}_{Q}$bezeichnet) im kartesischen Koordinatensystem

AlsOrtsvektor(auchRadiusvektor,PositionsvektoroderStützvektor) eines Punktes bezeichnet man in derMathematikund in derPhysikeinenVektor,der von einem festenBezugspunktzu diesem Punkt (Ort) zeigt.In der elementaren und in dersynthetischen Geometriekönnen diese Vektoren als Klassen von verschiebungsgleichen Pfeilen oder gleichwertig alsParallelverschiebungendefiniert werden.

Ortsvektoren ermöglichen es, für die Beschreibung vonPunkten,vonPunktmengenund vonAbbildungendie Vektorrechnung zu benutzen. Legt man einkartesisches Koordinatensystemzugrunde, dann wählt man in der Regel denKoordinatenursprungals Bezugspunkt für die Ortsvektoren der Punkte. In diesem Fall stimmen die Koordinaten eines Punktes bezüglich dieses Koordinatensystems mit den Koordinaten seines Ortsvektors überein.

In deranalytischen Geometriewerden Ortsvektoren verwendet, umAbbildungeneinesaffinenodereuklidischen Raumszu beschreiben und um Punktmengen (wie zum BeispielGeradenundEbenen) durch Gleichungen undParameterdarstellungenzu beschreiben.

In derPhysikwerden Ortsvektoren verwendet, um denOrteinesKörpersin einem euklidischen Raum zu beschreiben. Ortsvektoren zeigen beiKoordinatentransformationenein anderes Transformationsverhalten alskovariante Vektoren.

Schreibweisen

In der Geometrie wird der Bezugspunkt (Ursprung) in der Regel mit$O$(für lat.origo) bezeichnet. Die Schreibweise für den Ortsvektor eines Punktes$P$ist dann:

${\overrightarrow {OP}}$

Gelegentlich werden auch die Kleinbuchstaben mit Vektorpfeil benutzt, die den Großbuchstaben entsprechen, mit denen die Punkte bezeichnet werden, zum Beispiel:

${\vec {p}}={\overrightarrow {OP}},\ {\vec {q}}={\overrightarrow {OQ}},\ {\vec {a}}={\overrightarrow {OA}},\ {\vec {b}}={\overrightarrow {OB}},\ \dots,\ {\vec {x}}={\overrightarrow {OX}}$

Auch die Schreibweise, dass der Großbuchstabe, der den Punkt bezeichnet, mit einem Vektorpfeil versehen wird, ist üblich:

${\vec {P}}={\overrightarrow {OP}},\ {\vec {Q}}={\overrightarrow {OQ}},\ {\vec {A}}={\overrightarrow {OA}},\ {\vec {B}}={\overrightarrow {OB}},\ \dots,\ {\vec {X}}={\overrightarrow {OX}}$

Vor allem in der Physik wird der Ortsvektor auchRadiusvektorgenannt und mit Vektorpfeil als${\vec {r}}$oder (insbesondere in der theoretischen Physik) halbfett als$\mathbf {r}$geschrieben.

Beispiele und Anwendungen in der Geometrie

Verbindungsvektor

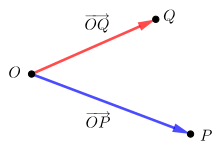
Der Verbindungsvektor${\overrightarrow {PQ}}$von Punkt$P$zu Punkt$Q$lässt sich mithilfe der Ortsvektoren${\vec {p}}={\overrightarrow {OP}}$und${\vec {q}}={\overrightarrow {OQ}}$darstellen:

${\overrightarrow {PQ}}={\overrightarrow {OQ}}-{\overrightarrow {OP}}={\vec {q}}-{\vec {p}}$

Kartesische Koordinaten

Für die Koordinaten des Ortsvektors${\overrightarrow {OP}}$des Punktes$P$mit den Koordinaten$(p_{1},p_{2},p_{3})$gilt:

${\overrightarrow {OP}}={\begin{pmatrix}p_{1}\\p_{2}\\p_{3}\end{pmatrix}}$

Verschiebung

EineVerschiebungum den Vektor${\vec {v}}$bildet den Punkt$X$auf den Punkt$X^{\prime }$ab. Dann gilt für die Ortsvektoren:

${\overrightarrow {OX'}}={\overrightarrow {OX}}+{\vec {v}}$

${\vec {x}}'={\vec {x}}+{\vec {v}}$

Drehung um den Ursprung

EineDrehungin der Ebene mit Drehzentrum$O$um denWinkel$\varphi$gegen denUhrzeigersinnkann in kartesischen Koordinaten wie folgt mit Hilfe einerDrehmatrixbeschrieben werden: Ist${\vec {x}}={\tbinom {x_{1}}{x_{2}}}={\overrightarrow {OX}}$der Ortsvektor eines Punktes$X$und${\vec {x}}'={\tbinom {x_{1}'}{x_{2}'}}={\overrightarrow {OX'}}$der Ortsvektor des Bildpunkts$X'$,so gilt:

${\begin{pmatrix}x_{1}'\\x_{2}'\end{pmatrix}}={\begin{pmatrix}\cos \varphi &-\sin \varphi \\\sin \varphi &\cos \varphi \end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}$

Affine Abbildung

Eine allgemeineaffine Abbildung,die den Punkt$X$auf den Punkt$X'$abbildet, kann mit Ortsvektoren wie folgt dargestellt werden:

${\vec {x}}'=L({\vec {x}})+{\vec {v}}$

Hierbei ist${\vec {x}}$der Ortsvektor von$X$,${\vec {x}}'$der Ortsvektor von$X'$,$L$eine lineare Abbildung und${\vec {v}}$ein Vektor, der eine Verschiebung beschreibt. In kartesischen Koordinaten kann die lineare Abbildung$L$durch eine Matrix$A$dargestellt werden und es gilt:

${\vec {x}}=A\cdot {\vec {x}}+{\vec {v}}$

Im dreidimensionalen Raum ergibt dies:

${\begin{pmatrix}x_{1}'\\x_{2}'\\x_{3}'\end{pmatrix}}={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}\,{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}+{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}$

Entsprechende Darstellungen gibt es auch für andere Dimensionen.

Parameterdarstellung einer Geraden

Die Gerade durch die Punkte$P$und$Q$enthält genau die Punkte$X$,deren Ortsvektor${\vec {x}}$die Darstellung

${\vec {x}}={\overrightarrow {OP}}+t\,{\overrightarrow {PQ}}$mit$t\in \mathbb {R}$

besitzt. Man spricht hier auch von derParameterformeinerGeradengleichung.

Normalenform der Ebenengleichung

Die Ebene durch den Punkt$P$(Stützpunkt)mitNormalenvektor${\vec {n}}$enthält genau die Punkte$X$,deren Ortsvektor${\vec {x}}$dieNormalengleichung

${\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}$

erfüllt. Dabei ist${\vec {p}}$der Ortsvektor(Stützvektor)des Stützpunkts$P$und der Malpunkt bezeichnet dasSkalarprodukt.

Ortsvektor in verschiedenen Koordinatensystemen

Kartesisches Koordinatensystem

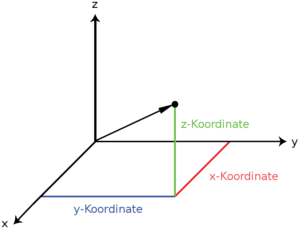
Der durch einen Ortsvektor beschriebene Punkt kann durch die Koordinaten eines Koordinatensystems ausgedrückt werden, wobei der Bezugspunkt des Ortsvektors normalerweise in denKoordinatenursprunggelegt wird.

Kartesische Koordinaten

Üblicherweise wird der Ortsvektor inkartesischen Koordinatenin der Form

${\vec {r}}={\vec {r}}\,(x,y,z)={\begin{pmatrix}x\\y\\z\end{pmatrix}}$

definiert. Daher sind die kartesischen Koordinaten gleichzeitig die Komponenten des Ortsvektors.

Zylinderkoordinaten

Der Ortsvektor als Funktion vonZylinderkoordinatenergibt sich durch Umrechnen der Zylinderkoordinaten in die entsprechenden kartesischen Koordinaten zu

${\vec {r}}={\vec {r}}\,(\rho,\varphi,z)={\begin{pmatrix}\rho \,\cos \varphi \\\rho \,\sin \varphi \\z\end{pmatrix}}.$

Hier bezeichnet$\rho$den Abstand des Punktes von der$z$-Achse, der Winkel$\phi$wird von der$x$-Achse in Richtung der$y$-Achse gezählt.$\rho$und$\varphi$sind also die Polarkoordinaten des orthogonal auf die$x$-$y$-Ebene projizierten Punktes.

Mathematisch gesehen wird hier dieAbbildung(Funktion) betrachtet, die den Zylinderkoordinaten$(\rho,\varphi,z)$die kartesischen Koordinaten$(x,y,z)$des Ortsvektors zuordnet.

Kugelkoordinaten

Kugelkoordinatensystem

Der Ortsvektor als Funktion vonKugelkoordinatenergibt sich durch Umrechnen der Kugelkoordinaten in die entsprechenden kartesischen Koordinaten zu

${\vec {r}}={\vec {r}}\,(r,\theta,\varphi )={\begin{pmatrix}r\,\sin \theta \,\cos \varphi \\r\,\sin \theta \,\sin \varphi \\r\,\cos \theta \end{pmatrix}}.$

Hierbei bezeichnet$r$den Abstand des Punktes vom Ursprung (also die Länge des Ortsvektors), der Winkel$\varphi$wird in der$x$-$y$-Ebene von der$x$-Achse aus in Richtung der$y$-Achse gemessen, der Winkel$\theta$ist der Winkel zwischen der$z$-Achse und dem Ortsvektor.

Physik

Himmelsmechanik

Um die Position einesHimmelskörpers,der sich auf einerUmlaufbahnum einSchwerezentrumbewegt, anzugeben, wird in derHimmelsmechanikals Ursprung des Orts- oder Radiusvektors dieses Schwerezentrum gewählt. Der Radiusvektor liegt dann stets in Richtung derGravitationskraft.DieStreckedes Ortsvektors wirdFahrstrahlgenannt. Der Fahrstrahl spielt eine zentrale Rolle beimzweiten Keplerschen Gesetz (Flächensatz).

Siehe auch

• Einheitsvektor
• Frenetsche Formeln
• Hodograph

Literatur

• Klaus Desch:Mathematische Ergaenzungen zur Physik II, Kapitel 11: Vektoranalysis.(PDF, 210 kB). Institut für Experimentalphysik, Hamburg.