Quadrik

Quadriken im dreidimensionalen Raum: ein- und zweischaligesHyperboloid,Ellipsoid,hyperbolischesParaboloid,Zylinder,elliptisches Paraboloid undKegel(von links nach rechts)

EineQuadrik(vonlateinischquadraQuadrat) ist in derMathematikdieLösungsmengeeinerquadratischen Gleichungmehrerer Unbekannter. In zwei Dimensionen bildet eine Quadrik im Regelfall eineKurvein derEbene,wobei es sich dann um einenKegelschnitthandelt. In drei Dimensionen beschreibt eine Quadrik im Regelfall eineFlächeimRaum,die auchFläche zweiter Ordnungoderquadratische Flächegenannt wird. Allgemein handelt es sich bei einer Quadrik um einealgebraische Varietät,also um eine spezielleHyperfläche,in einem endlichdimensionalen reellenKoordinatenraum.Durch eineHauptachsentransformationlässt sich jede Quadrik auf eine von drei möglichenNormalformentransformieren. Auf diese Weise können Quadriken in verschiedene grundlegende Typen klassifiziert werden.

Quadriken werden insbesondere in deranalytischenund derprojektiven Geometrieuntersucht. Anwendungen für Quadriken in Technik und Naturwissenschaften finden sich unter anderem in der Geodäsie (Referenzellipsoid), der Architektur (Tragwerkskonstruktion) oder der Optik (Parabolspiegel).

Die jeweilige Quadrik, d. h. Lösungsmenge, wird im Folgenden mit${\textstyle Q}$bezeichnet. Darüber hinaus wird auf dieser Seite zur möglichst einfachen Unterscheidung der verwendetenSymboledie folgende in derLinearen AlgebraüblicheNotationverwendet:

$a$repräsentiert eine reelle Zahl,
$\mathrm {a}$einen Vektor (aufrecht in Kleinbuchstaben),
$\mathrm {A}$eine Matrix (aufrecht in Großbuchstaben).

Definition

Eine Quadrik ist einePunktmengeim$n$-dimensionalen reellenKoordinatenraum$\mathbb {R} ^{n}$der Form

$Q=\left\{(x_{1},\ldots,x_{n})\in \mathbb {R} ^{n}\mid q(x_{1},\ldots,x_{n})=0\right\}$,

wobei

$q(x_{1},\ldots,x_{n})=\sum _{i,j=1}^{n}a_{ij}x_{i}x_{j}+2\,\sum _{i=1}^{n}b_{i}x_{i}+c$

einquadratisches Polynomin den Variablen$x_{1},\ldots,x_{n}$ist. Mindestens einer der Polynomkoeffizienten$a_{11},\dots,a_{nn}$muss dabei ungleich null sein. Zudem kannohne Einschränkungvorausgesetzt werden, dass$a_{ij}=a_{ji}$für alle$i,j\in \{1,\dotsc,n\}$gilt. Eine Quadrik ist damit dieNullstellenmengeeines quadratischen Polynoms mehrerer Variablen beziehungsweise dieLösungsmengeeinerquadratischen Gleichungmit mehreren Unbekannten.

Beispiele

Zum Beispiel beschreibt die Menge der Punkte

$Q=\left\{(x,y)\in \mathbb {R} ^{2}\mid 2x^{2}+3y^{2}=5\right\}$

eineEllipsein der Ebene. Die Menge der Punkte

$Q=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}-z^{2}=1\right\}$

beschreibt ein einschaligesHyperboloidim dreidimensionalen Raum.

Eigenschaften

Matrixdarstellung

In kompakterMatrixnotationkann eine Quadrik als eine Menge von Vektoren

$Q=\left\{\mathrm {x} \in \mathbb {R} ^{n}\mid \mathrm {x^{T}} \mathrm {A} \mathrm {x} +2\mathrm {b^{T}} \mathrm {x} +c=0\right\}$

beschrieben werden, wobei$\mathrm {A} =(a_{ij})\in \mathbb {R} ^{n\times n}$einesymmetrische Matrixund$\mathrm {b} =(b_{i})\in \mathbb {R} ^{n}$sowie$\mathrm {x} =(x_{i})\in \mathbb {R} ^{n}$Spaltenvektorenentsprechender Länge sind. Mit Hilfe der erweiterten Darstellungsmatrix

$\mathrm {\bar {A}} ={\begin{pmatrix}\mathrm {A} &\mathrm {b} \\\mathrm {b^{T}} &c\end{pmatrix}}$

und dementsprechend erweiterten Vektor$\mathrm {\bar {x}} ={\tbinom {\mathrm {x} }{1}}$kann eine Quadrik auch kompakt durch die Menge

$Q=\left\{\mathrm {x} \in \mathbb {R} ^{n}\mid \mathrm {{\bar {x}}^{T}} \mathrm {\bar {A}} \,\mathrm {\bar {x}} =0\right\}$

inhomogenen Koordinatendargestellt werden.

Typen

Bei Quadriken werden drei grundlegende Typen unterschieden. Die Entscheidung, um welchen Typ es sich bei einer gegebenen Quadrik handelt, kann anhand derRängeder Matrizen$\mathrm {A}$,$(\mathrm {A|b} )$und$\mathrm {\bar {A}}$getroffen werden:

• Kegeliger Typ:$\operatorname {rang} (\mathrm {\bar {A}} )=\operatorname {rang} (\mathrm {A|b} )=\operatorname {rang} (\mathrm {A} )$
• Mittelpunktsquadrik:$\operatorname {rang} (\mathrm {\bar {A}} )>\operatorname {rang} (\mathrm {A|b} )=\operatorname {rang} (\mathrm {A} )$
• Parabolischer Typ:$\operatorname {rang} (\mathrm {A|b} )>\operatorname {rang} (\mathrm {A} )$

Eine Quadrik heißt dabeiausgeartet,falls

$\det \mathrm {\bar {A}} =0$

gilt. Während nichtausgeartete Quadriken in allen Richtungen gekrümmte Hyperflächen bilden, weisen ausgeartete Quadriken in manchen Richtungen geradlinige Strukturen auf oder sind anderweitig degeneriert.

Transformationen

Quadriken lassen sich durchÄhnlichkeitsabbildungentransformieren, ohne dass sich ihr Typ dadurch verändert. Ist$\mathrm {S} \in \mathbb {R} ^{n\times n}$einereguläre Matrix,dann erhält man durch dielineare Transformation$\mathrm {y} =\mathrm {S^{-1}} \mathrm {x}$eine neue Quadrik in den Koordinaten$y_{1},\ldots,y_{n}$,die der Gleichung

${\begin{pmatrix}\mathrm {y^{T}} \!\!&1\end{pmatrix}}{\begin{pmatrix}\mathrm {S^{T}} &0\\0&1\end{pmatrix}}{\begin{pmatrix}\mathrm {A} &\mathrm {b} \\\mathrm {b^{T}} &c\end{pmatrix}}{\begin{pmatrix}\mathrm {S} &0\\0&1\end{pmatrix}}{\begin{pmatrix}\mathrm {y} \\1\end{pmatrix}}={\begin{pmatrix}\mathrm {y^{T}} \!\!&1\end{pmatrix}}{\begin{pmatrix}\mathrm {S^{T}AS} &\mathrm {S^{T}b} \\\mathrm {b^{T}S} &c\end{pmatrix}}{\begin{pmatrix}\mathrm {y} \\1\end{pmatrix}}=0$

genügt. Ebenso erhält man durch eineParallelverschiebung$\mathrm {y=x-u}$um einen Vektor$\mathrm {u} \in \mathbb {R} ^{n}$eine neue Quadrik, die die Gleichung

${\begin{pmatrix}\mathrm {y^{T}} \!\!&1\end{pmatrix}}{\begin{pmatrix}\mathrm {I} &0\\\mathrm {u^{T}} &1\end{pmatrix}}{\begin{pmatrix}\mathrm {A} &\mathrm {b} \\\mathrm {b^{T}} &c\end{pmatrix}}{\begin{pmatrix}\mathrm {I} &\mathrm {u} \\0&1\end{pmatrix}}{\begin{pmatrix}\mathrm {y} \\1\end{pmatrix}}={\begin{pmatrix}\mathrm {y^{T}} \!\!&1\end{pmatrix}}{\begin{pmatrix}\mathrm {A} &\mathrm {Au+b} \\\mathrm {u^{T}A+b^{T}} &\mathrm {u^{T}Au+2b^{T}u} +c\end{pmatrix}}{\begin{pmatrix}\mathrm {y} \\1\end{pmatrix}}=0$

mit derEinheitsmatrix$\mathrm {I} \in \mathbb {R} ^{n\times n}$erfüllt. Insbesondere ändert sich der Rang der Matrizen$\mathrm {A,(A\mid b)}$und$\mathrm {\bar {A}}$durch solcheAffinitätennicht.

Ist$\det(\mathrm {A} )\neq 0$,so lassen sich beide Methoden mittels$\mathrm {y=S^{-1}x}$und$\mathrm {z=y+S^{-1}A^{-1}b}$zu$\mathrm {z=S^{-1}(x+A^{-1}b)}$kombinieren:

${\begin{pmatrix}\mathrm {z^{T}} \!\!&1\end{pmatrix}}{\begin{pmatrix}\mathrm {S^{T}} &0\\\mathrm {-b^{T}A^{-1}} &1\end{pmatrix}}{\begin{pmatrix}\mathrm {A} &\mathrm {b} \\\mathrm {b^{T}} &c\end{pmatrix}}{\begin{pmatrix}\mathrm {S} &\mathrm {-A^{-1}b} \\0&1\end{pmatrix}}{\begin{pmatrix}\mathrm {z} \\1\end{pmatrix}}={\begin{pmatrix}\mathrm {z^{T}} \!\!&1\end{pmatrix}}{\begin{pmatrix}\mathrm {S^{T}AS} &0\\0&\mathrm {-b^{T}A^{-1}b} +c\end{pmatrix}}{\begin{pmatrix}\mathrm {z} \\1\end{pmatrix}}=0.$

Da die Matrix$\mathrm {A}$symmetrisch ist, ist sie orthogonal diagonalisierbar, das heißt, es gibt eine orthogonale Matrix$\mathrm {S}$,so dass$\mathrm {S^{-1}AS=S^{T}AS=:D}$eine Diagonalmatrix ist. Damit kann die Quadrik durch die Bedingung

$\mathrm {z^{T}Dz-b^{T}A^{-1}b} +c=0$

ausgedrückt werden. Es kommen also keine gemischt-quadratischen und keine linearen Terme mehr vor. Der Mittelpunkt der Quadrik liegt somit bei$\mathrm {z=0} \Leftrightarrow \mathrm {x=-A^{-1}b}$.

Normalformen

Durch eineHauptachsentransformationlässt sich jede Quadrik auf eine der folgendenNormalformentransformieren. Hierzu wird zunächst eineorthogonale Matrix$\mathrm {S}$,beispielsweise eineDreh-oderSpiegelungsmatrix,derart gewählt, dass$\mathrm {S^{T}AS}$eineDiagonalmatrixergibt, die dieEigenwertevon$\mathrm {A}$in absteigender Reihenfolge enthält. Im zweiten Schritt wird die transformierte Quadrik derart um einen Vektor$\mathrm {u}$verschoben, dass auch die linearen Terme und der konstante Term weitestgehend verschwinden. Schließlich wird die Quadrik noch so normiert, dass der konstante Term, sofern er nicht null ist, zu eins wird. Dadurch ergeben sich die folgenden drei Normalformen:

• Kegeliger Typ:${\frac {x_{1}^{2}}{\alpha _{1}^{2}}}+\dotsb +{\frac {x_{p}^{2}}{\alpha _{p}^{2}}}-{\frac {x_{p+1}^{2}}{\alpha _{p+1}^{2}}}-\dotsb -{\frac {x_{r}^{2}}{\alpha _{r}^{2}}}=0$mit$1\leq p\leq r\leq n,\ p\geq r-p$
• Mittelpunktsquadrik:${\frac {x_{1}^{2}}{\alpha _{1}^{2}}}+\dotsb +{\frac {x_{p}^{2}}{\alpha _{p}^{2}}}-{\frac {x_{p+1}^{2}}{\alpha _{p+1}^{2}}}-\dotsb -{\frac {x_{r}^{2}}{\alpha _{r}^{2}}}=1$mit$1\leq p\leq r\leq n$
• Parabolischer Typ:${\frac {x_{1}^{2}}{\alpha _{1}^{2}}}+\dotsb +{\frac {x_{p}^{2}}{\alpha _{p}^{2}}}-{\frac {x_{p+1}^{2}}{\alpha _{p+1}^{2}}}-\dotsb -{\frac {x_{r}^{2}}{\alpha _{r}^{2}}}-2x_{r+1}=0$mit$1\leq p\leq r<n,\ p\geq r-p$

Hinzu kommt als Spezialfall die

• Leere Menge:$-{\frac {x_{1}^{2}}{\alpha _{1}^{2}}}-\dotsb -{\frac {x_{r}^{2}}{\alpha _{r}^{2}}}=1$mit$1\leq r\leq n$

In allen Fällen sind die Koeffizienten$\alpha _{1},\dotsc,\alpha _{r}>0$.Die Kennzahlen$p=|\{\lambda \in \sigma (\mathrm {A} )\colon \lambda >0\}|$und$r=|\{\lambda \in \sigma (\mathrm {A} )\colon \lambda \neq 0\}|=\operatorname {rang} (\mathrm {A} )$ergeben sich dabei aus derSignaturder Matrix$\mathrm {A}$.

Klassifikation

Quadriken in einer Dimension

In einer Dimension ist eine Quadrik die Lösungsmenge einerquadratischen Gleichungmit einer Unbekannten, also eine Punktmenge der Form

$Q=\left\{x\in \mathbb {R} \mid ax^{2}+bx+c=0\right\}$.

Durch Verschiebung (quadratische Ergänzung) und Normierung lassen sich die folgenden zwei Fälle unterscheiden:

Nicht ausgeartete Quadriken		Ausgeartete Quadriken
Zwei Lösungen ${x^{2} \over \alpha ^{2}}=1$		Eine Lösung ${x^{2} \over \alpha ^{2}}=0$

In dem verbleibenden Fall$-{\tfrac {x^{2}}{\alpha ^{2}}}=1$ergibt sich als Lösungsmenge die leere Menge. In allen Fällen ist$\alpha >0$.

Quadriken in der Ebene

In der Ebene ist eine Quadrik die Lösungsmenge einer quadratischen Gleichung mit zwei Unbekannten, also eine Punktmenge der Form

$Q=\left\{(x,y)\in \mathbb {R} ^{2}\mid ax^{2}+bxy+cy^{2}+dx+ey+f=0\right\}$.

Hierbei handelt es sich bis auf degenerierte Fälle umKegelschnitte,wobei ausgeartete Kegelschnitte, bei denen die Kegelspitze in der Schnittebene enthalten ist, von nicht ausgearteten Kegelschnitten unterschieden werden. Durch Hauptachsentransformation lässt sich die allgemeine Gleichung einer Quadrik auf eine der folgenden Normalformen transformieren:

Nicht ausgeartete Quadriken		Ausgeartete Quadriken
Ellipse ${x^{2} \over \alpha ^{2}}+{y^{2} \over \beta ^{2}}=1$		Zwei schneidendeGeraden ${x^{2} \over \alpha ^{2}}-{y^{2} \over \beta ^{2}}=0$
Hyperbel ${x^{2} \over \alpha ^{2}}-{y^{2} \over \beta ^{2}}=1$		Zwei parallele Geraden ${x^{2} \over \alpha ^{2}}=1$
Parabel ${x^{2} \over \alpha ^{2}}-2y=0$		Eine Gerade ${x^{2} \over \alpha ^{2}}=0$
		EinPunkt ${\frac {x^{2}}{\alpha ^{2}}}+{\frac {y^{2}}{\beta ^{2}}}=0$

In den beiden verbleibenden Fällen$-{\tfrac {x^{2}}{\alpha ^{2}}}-{\tfrac {y^{2}}{\beta ^{2}}}=1$und$-{\tfrac {x^{2}}{\alpha ^{2}}}=1$ergibt sich als Lösungsmenge jeweils die leere Menge. In allen Fällen sind$\alpha,\beta >0$.

Quadriken im Raum

Im dreidimensionalen Raum ist eine Quadrik die Lösungsmenge einer quadratischen Gleichung mit drei Unbekannten, also eine Punktmenge der Form

$Q=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid ax^{2}+bxy+cxz+dy^{2}+eyz+fz^{2}+gx+hy+iz+j=0\right\}$.

Im Raum ist die Vielfalt der Quadriken deutlich größer als in der Ebene. Hier gibt es ebenfalls ausgeartete und nicht ausgeartete Quadriken. Unter den ausgearteten Quadriken finden sich dabei auch einfach gekrümmte Flächen, wie Zylinder und Kegel. Ähnlich wie in zwei Dimensionen lässt sich die allgemeine Gleichung einer Quadrik auf eine der folgenden Normalformen transformieren:

Nicht ausgeartete Quadriken		Ausgeartete Quadriken (gekrümmte Flächen)		Ausgeartete Quadriken (Ebenen u. a.)
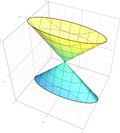
Ellipsoid ${x^{2} \over \alpha ^{2}}+{y^{2} \over \beta ^{2}}+{z^{2} \over \gamma ^{2}}=1$		Elliptischer Kegel ${x^{2} \over \alpha ^{2}}+{y^{2} \over \beta ^{2}}-{z^{2} \over \gamma ^{2}}=0$		Zwei schneidende Ebenen ${\frac {x^{2}}{\alpha ^{2}}}-{\frac {y^{2}}{\beta ^{2}}}=0$
Einschaliges Hyperboloid ${x^{2} \over \alpha ^{2}}+{y^{2} \over \beta ^{2}}-{z^{2} \over \gamma ^{2}}=1$		Elliptischer Zylinder ${x^{2} \over \alpha ^{2}}+{y^{2} \over \beta ^{2}}=1$		Zwei parallele Ebenen ${\frac {x^{2}}{\alpha ^{2}}}=1$
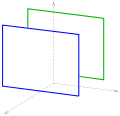
Zweischaliges Hyperboloid ${x^{2} \over \alpha ^{2}}+{y^{2} \over \beta ^{2}}-{z^{2} \over \gamma ^{2}}=-1$		Hyperbolischer Zylinder ${x^{2} \over \alpha ^{2}}-{y^{2} \over \beta ^{2}}=1$		Eine Ebene ${x^{2} \over \alpha ^{2}}=0$
Elliptisches Paraboloid ${x^{2} \over \alpha ^{2}}+{y^{2} \over \beta ^{2}}-2z=0$		Parabolischer Zylinder ${x^{2} \over \alpha ^{2}}-2y=0$		Eine Gerade ${\frac {x^{2}}{\alpha ^{2}}}+{\frac {y^{2}}{\beta ^{2}}}=0$
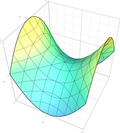
Hyperbolisches Paraboloid ${x^{2} \over \alpha ^{2}}-{y^{2} \over \beta ^{2}}-2z=0$				Ein Punkt ${\frac {x^{2}}{\alpha ^{2}}}+{\frac {y^{2}}{\beta ^{2}}}+{\frac {z^{2}}{\gamma ^{2}}}=0$

In den drei verbleibenden Fällen$-{\tfrac {x^{2}}{\alpha ^{2}}}-{\tfrac {y^{2}}{\beta ^{2}}}-{\tfrac {z^{2}}{\gamma ^{2}}}=1$,$-{\tfrac {x^{2}}{\alpha ^{2}}}-{\tfrac {y^{2}}{\beta ^{2}}}=1$und$-{\tfrac {x^{2}}{\alpha ^{2}}}=1$ergibt sich als Lösungsmenge wiederum jeweils die leere Menge. In allen Fällen sind$\alpha,\beta,\gamma >0$.

Für$\alpha =\beta$(bzw.$\beta =\gamma$im Fall des zweischaligen Hyperboloids) erhält man in folgenden FällenRotationsflächen,die auch alsDrehquadrikenbezeichnet werden:Rotationsellipsoid,ein- und zweischaligesRotationshyperboloid,Rotationsparaboloid,KreiskegelundKreiszylinder.Regelflächen,also Flächen, die von einer einparametrigenGeradenscharerzeugt werden, sind Kegel, elliptischer und parabolischer Zylinder, Ebene, einschaliges Hyperboloid und hyperbolisches Paraboloid. Die letzteren drei Flächen werden sogar von zwei Geradenscharen erzeugt und sind die einzig möglichen doppelt gekrümmten Regelflächen im Raum.

Projektive Quadriken

→Hauptartikel:Projektive Quadrik

Die Vielfalt der Quadriken verringert sich erheblich, wenn man sowohl den affinen Raum, in dem eine Quadrik definiert ist, als auch die Quadrik selbstprojektivabschließt. Die projektiven Erweiterungen von Ellipsen, Hyperbeln und Parabeln sind projektiv alle zueinander äquivalent, das heißt, es gibt eine projektiveKollineation,die die eine Kurve auf die andere abbildet (sieheprojektiver Kegelschnitt).

Im dreidimensionalen Raum sind folgende Quadriken äquivalent:

• Ellipsoid, zweischaliges Hyperboloid und elliptisches Paraboloid,
• einschaliges Hyperboloid und hyperbolisches Paraboloid,
• elliptischer, hyperbolischer, parabolischer Zylinder und Kegel.

Verallgemeinerungen

Allgemeiner können Quadriken auch in Vektorräumen über einem beliebigenKörper,also auch über dem Körper derkomplexen Zahlenoder auch überendlichen Körpernbetrachtet werden.

Literatur

• Ilja Nikolajewitsch Bronstein, Konstantin A. Semendjajew:Taschenbuch der Mathematik.Teubner-Verlag, Leipzig 1983,ISBN 3-87144-492-8,S. 283.
• Klemens Burg, Herbert Haf, Friedrich Wille:Höhere Mathematik für Ingenieure.Band II, Teubner-Verlag, Stuttgart,ISBN 3-519-22956-0,S. 341.
• dtv-Atlas zur Mathematik.Band 1, Deutscher Taschenbuch-Verlag,ISBN 3-423-03007-0,S. 200–203.
• Kurt Meyberg, Peter Vachenauer:Höhere Mathematik 1.Springer-Verlag, Berlin 1995,ISBN 3-540-59188-5,S. 343.

Weblinks

Commons:Quadric surfaces– Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Quadrik– Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• V. S. Malakhovskii:Quadric.In:Michiel Hazewinkel(Hrsg.):Encyclopedia of Mathematics.Springer-Verlag undEMSPress, Berlin 2002,ISBN 1-55608-010-7(englisch,encyclopediaofmath.org).
• Eric W. Weisstein:Quadratic Surface.In:MathWorld(englisch).
• pahio:Quadratic Surfaces.In:PlanetMath.(englisch)
• Bilder von Quadriken im Raum
• Interaktive 3D-Modelle aller Quadriken