Umkreis

In der ebenenGeometrieist einUmkreiseinKreis,der durch alleEckpunkteeinesPolygons(Vielecks) geht.

Nicht für jedes Polygon existiert ein solcher Umkreis. Allgemein besitzt einkonvexesPolygon genau dann einen Umkreis, wenn dieMittelsenkrechtenaller Seiten einander in einem Punkt schneiden. In diesem Fall ist der gemeinsame Punkt der Mittelpunkt des Umkreises.

Umkreis eines Dreiecks

Dreieck mit Mittelsenkrechten und Umkreis

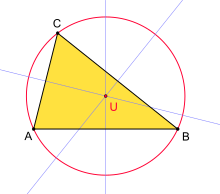
Eine besonders große Bedeutung hat der Umkreis in derDreiecksgeometrie.Jedes (nichtentartete)Dreieckbesitzt einen Umkreis, wie im Folgenden begründet wird.

Alle Punkte der Mittelsenkrechten zu $[AB]$ sind von $A$ und $B$ gleich weit entfernt. Entsprechend haben die Punkte der Mittelsenkrechten zu $[BC]$ übereinstimmende Entfernungen von $B$ und $C$ .Der Schnittpunkt dieser beiden Mittelsenkrechten ist daher von allen drei Ecken ( $A$ , $B$ und $C$ ) gleich weit entfernt (er existiert, weil die drei Eckpunkte eines Dreiecks nichtkollinearsind). Er muss also auch auf der dritten Mittelsenkrechten liegen. Zeichnet man um diesen Schnittpunkt einen Kreis, der durch eine Ecke des Dreiecks geht, so müssen auch die anderen Ecken auf diesem Kreis liegen.

Der Umkreismittelpunkt, also der Schnittpunkt der Mittelsenkrechten, zählt zu denausgezeichneten Punktendes Dreiecks. Er trägt dieKimberling-Nummer $X_{3}$ .

Sonderfälle

Beimspitzwinkligen Dreieckliegt der Umkreismittelpunkt im Inneren des Dreiecks.

Beimrechtwinkligen Dreieckist der Mittelpunkt der Hypotenuse zugleich Umkreismittelpunkt (sieheSatz des Thales).

Beimstumpfwinkligen Dreieck(mit einem Winkel über 90°) befindet sich der Umkreismittelpunkt außerhalb des Dreiecks.

Radius

Der Umkreisradius eines Dreiecks lässt sich mit demSinussatzberechnen:

r_{u}={\frac {a}{2\cdot \sin(\alpha )}}={\frac {b}{2\cdot \sin(\beta )}}={\frac {c}{2\cdot \sin(\gamma )}}

Dabei stehen die Bezeichnungen $a$ , $b$ , $c$ für die Seitenlängen und $\alpha$ , $\beta$ , $\gamma$ für die Größen der den Seiten mit den Längen $a,b,c$ gegenüberliegendenInnenwinkel.DurchErweiternobiger Brüche mit einer Dreiecksseite entstehen Formeln mit den Höhen $h_{a}$ , $h_{b}$ und $h_{c}$ der von $A$ , $B$ bzw. $C$ ausgehenden Höhen des Dreiecks $ABC$ :^[1]

r_{u}={\frac {ab}{2h_{c}}}={\frac {bc}{2h_{a}}}={\frac {ca}{2h_{b}}}

DerFlächeninhalt $A$ lässt sich z. B. mit Hilfe derheronischen Formelberechnen und es gilt:

r_{u}={\frac {a\cdot b\cdot c}{4\cdot A}}

.

Für den Umkreisradius imgleichseitigen Dreieckist speziell

r_{u}={\frac {a}{\sqrt {3}}}

.

Koordinaten

Diekartesischen Koordinatendes Umkreismittelpunkts $(x_{u},y_{u})$ können aus den kartesischen Koordinaten der Eckpunkte berechnet werden. Die Koordinaten der drei Eckpunkte seien $(x_{1},y_{1})$ , $(x_{2},y_{2})$ und $(x_{3},y_{3})$ .

Mit den Determinanten

A=\det {\begin{pmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{pmatrix}}

B=\det {\begin{pmatrix}x_{1}^{2}+y_{1}^{2}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&y_{3}&1\end{pmatrix}}

C=\det {\begin{pmatrix}x_{1}^{2}+y_{1}^{2}&x_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&1\end{pmatrix}}

D=\det {\begin{pmatrix}x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}\end{pmatrix}}

Ergibt sich $x_{M}={\frac {B}{2A}}$ , $y_{M}={\frac {-C}{2A}}$ und $r={\sqrt {{\frac {B^{2}+C^{2}}{4A^{2}}}+{\frac {D}{A}}}}$ .

Liegen die Punkte auf einer Geraden, so ist $A=0$ und es gibt keine Lösung.

Ohne Matrizen formuliert gilt:

Mit

d=2(x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}))

ergeben sich die kartesischen Koordinaten des Umkreismittelpunkts zu

x_{u}={\frac {(x_{1}^{2}+y_{1}^{2})(y_{2}-y_{3})+(x_{2}^{2}+y_{2}^{2})(y_{3}-y_{1})+(x_{3}^{2}+y_{3}^{2})(y_{1}-y_{2})}{d}}

und

y_{u}={\frac {(x_{1}^{2}+y_{1}^{2})(x_{3}-x_{2})+(x_{2}^{2}+y_{2}^{2})(x_{1}-x_{3})+(x_{3}^{2}+y_{3}^{2})(x_{2}-x_{1})}{d}}

.

Umkreismittelpunkt eines Dreiecks $\left(X_{3}\right)$
Trilineare Koordinaten	$\cos \alpha \,:\,\cos \beta \,:\,\cos \gamma$ $=a(b^{2}+c^{2}-a^{2})\,:\,b(c^{2}+a^{2}-b^{2})\,:\,c(a^{2}+b^{2}-c^{2})$
Baryzentrische Koordinaten	$\sin(2\alpha )\,:\,\sin(2\beta )\,:\,\sin(2\gamma )$

Weitere Eigenschaften

Der Umkreismittelpunkt liegt wie derSchwerpunktund derHöhenschnittpunktauf dereulerschen Geraden.
Nach demSüdpolsatzschneidet sich die Mittelsenkrechte einer Dreiecksseite mit derWinkelhalbierendendes gegenüberliegendenWinkelsstets auf dem Umkreis.
Die Entfernung zwischen Umkreismittelpunkt und Inkreismittelpunkt beträgt ${\sqrt {R(R-2r)}}$ ,wobei $R$ den Umkreisradius und $r$ den Inkreisradius bezeichnet (Satz von Euler).
Die Summe der vorzeichenbehaftetenAbständedes Umkreismittelpunktes von den Dreiecksseiten ist gleich der Summe aus Umkreis- und Inkreisradius (sieheSatz von Carnot).
DerSatz vom Dreizackstellt einen Zusammenhang zwischen Umkreis undInkreisher.
Der Umkreis ist dergeometrische Ortaller Punkte, derenOrthogonalprojektionenauf die Dreiecksseiten kollinear sind.^[2]

Verallgemeinerung: Mittellotensatz

Die Aussage, dass sich die Mittelsenkrechten der Dreiecksseiten in einem Punkt schneiden, wird in dersynthetischen GeometriealsMittellotensatzbezeichnet. Dort kann für allgemeinere affine Ebenen, in denen kein Abstandsbegriff und damit keine „Kreise “definiert sind, gezeigt werden, dass dieser Satz äquivalent zumHöhenschnittpunktsatzist. → Siehe dazuHöhenschnittpunktundpräeuklidische Ebene.

Umkreise von Dreiecken aus einem orthozentrischen Quadrupel

Gegeben sei ein Dreieck $ABC$ und sein Höhenschnittpunkt $H$ .Dann haben die von drei der vier Punkte $A$ , $B$ , $C$ und $H$ gebildeten DreieckekongruenteUmkreise.

Die vier Punkte $A$ , $B$ , $C$ und $H$ werden auch alsorthozentrischesQuadrupelbezeichnet.

Beweis:

Ohne Beschränkung der Allgemeinheitwird die Kongruenz der Umkreise für die beiden Dreiecke $ABC$ und $ABH$ gezeigt. Im Dreieck $ABE$ ergänzen sich der rot markierte Winkel $\angle HBF$ und der Winkel $\angle FAE$ zu 90°. Ebenso ergänzen sich im Dreieck $CAF$ der rot markierte Winkel $\angle ECH$ und der Winkel $\angle FAE$ zu 90°. Hieraus folgt, dass die beiden rot markierten Winkel gleich groß sind.

Der Punkt $P$ ist der zweite Schnittpunkt des Umkreises des Dreiecks $ABC$ mit der verlängerten Dreieckshöhe durch $C$ .Der rot markierte Winkel $\angle ECH$ und der grün markierte Winkel $\angle FBP$ sind alsUmfangswinkelamKreisbogenüber $AP$ gleich groß. Damit sind auch der rot markierte Winkel $\angle HBF$ und der grün markierte Winkel $\angle FBP$ gleich groß. Folglich sind nach demKongruenzsatzWSWdann auch dierechtwinkligen Dreiecke $BHF$ und $PBF$ kongruent. Somit sind nach dem KongruenzsatzSWSauch die Dreiecke $ABH$ und $BAP$ kongruent, also sind auch ihre Umkreise kongruent.

Da der Umkreis des Dreiecks $BAP$ auch der des Dreiecks $ABC$ ist und die Umkreise der Dreiecke $ABH$ und $BAP$ kongruent sind, haben auch die Dreiecke $ABC$ und $ABH$ kongruente Umkreise. Damit ist die Aussage bewiesen.^[3]

Umkreise anderer Vielecke

Während beim Dreieck stets ein Umkreis existiert, trifft dies bei Vielecken (Polygonen) mit mehr als drei Ecken nur in besonderen Fällen zu.

Vierecke,die einen Umkreis haben, werdenSehnenviereckegenannt. Spezialfälle sindgleichschenklige Trapeze,also auchRechteckeundQuadrate.

Unabhängig von der Eckenzahl hat jedesregelmäßige Polygoneinen Umkreis. Für den Umkreisradius eines regelmäßigen $n$ -Ecks mit der Seitenlänge $a$ gilt:

R={\frac {a}{2\sin {\frac {180^{\circ }}{n}}}}

Weblinks

Wiktionary: Umkreis– Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Walter-Fendt.de(Umkreis-Konstruktion wird Schritt für Schritt vorgeführt)
Flash-Animation zur Umkreis-Konstruktion beim Dreieck(Mementovom 7. Januar 2010 imInternet Archive) (dwu-Unterrichtsmaterialien)

Einzelnachweise

↑R. A. Johnson:Advanced Euclidean Geometry.An Elementary Treatise on the Geometry of the Triangle and the Circle. Dover Publications, New York 1960,ISBN 978-0-486-15498-5,S.71(idoc.pub).
↑John Casey:A sequel to the first six books of the Elements of Euclid, containing an easy introduction to modern geometry, with numerous examples.Hodges, Figgis & co., Dublin 1886,S.34(archive.org– Prop. 12, Cor. 1).
↑Günter Aumann:Kreisgeometrie. Eine elementare Einführung.Springer Spektrum,Springer-Verlag Berlin Heidelberg 2015,ISBN 978-3-662-45305-6,Seiten 29 und 30.

[Johnson-1] R. A. Johnson:Advanced Euclidean Geometry.An Elementary Treatise on the Geometry of the Triangle and the Circle. Dover Publications, New York 1960,ISBN 978-0-486-15498-5,S.71(idoc.pub).

[2] John Casey:A sequel to the first six books of the Elements of Euclid, containing an easy introduction to modern geometry, with numerous examples.Hodges, Figgis & co., Dublin 1886,S.34(archive.org– Prop. 12, Cor. 1).

[3] Günter Aumann:Kreisgeometrie. Eine elementare Einführung.Springer Spektrum,Springer-Verlag Berlin Heidelberg 2015,ISBN 978-3-662-45305-6,Seiten 29 und 30.

[1]

[2]

[3]

Umkreis

Inhaltsverzeichnis