Satz des Thales

Satz des Thales

DerSatz des Thalesist einSatzderGeometrieund ein Spezialfall desKreiswinkelsatzes.Vereinfacht lautet er:Alle von einemHalbkreisumschriebenenDreieckesindrechtwinklig.

Der ersteBeweiswird dem antiken griechischenMathematikerundPhilosophenThales von Miletzugeschrieben.Die Aussage des Satzes war bereits vorher inÄgyptenundBabylonienbekannt.

Formulierung des Satzes und seiner Umkehrung

Halbkreismitrechtwinkligen Dreiecken

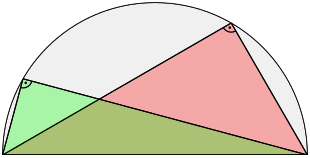
Exakte Formulierung: Konstruiert man ein Dreieck aus den beiden EndpunktendesDurchmesserseinesHalbkreises(Thaleskreis) und einem weiteren Punkt dieses Halbkreises, so erhält man immer einrechtwinkliges Dreieck.

Oder: Liegt der Punkt$C$eines Dreiecks$ABC$auf einem Halbkreis über derStrecke${\overline {AB}}$,dann hat das Dreieck bei$C$immer einenrechten Winkel.

Auch die Umkehrung des Satzes ist korrekt: DerMittelpunktdesUmkreiseseines rechtwinkligen Dreiecks liegt immer in der Mitte derHypotenuse,also der längsten Seite des Dreiecks, die dem rechten Winkel gegenüberliegt.

Oder: Hat das Dreieck$ABC$bei$C$einen rechtenWinkel,so liegt$C$auf einemKreismit derHypotenuse${\overline {AB}}$alsDurchmesser.

Beweise

Euklid leitet den Satz des Thales im dritten Band seinerElementemit Hilfe folgender Sätze, die ebenfalls Thales zugeschrieben werden und im ersten Band enthalten sind, her:

Beweis mit gleichschenkligen Dreiecken

• In jedemgleichschenkligen Dreiecksind dieWinkelan der Basis gleich.
• DieInnenwinkelsummeim Dreieck ist 180°.

Zerlegung des Dreiecks unter demHalbkreisin zweigleichschenklige Dreiecke.DieWinkel$\gamma$und$\delta$ergänzen sich zu 180°, die Winkel$\ Alpha$und$\beta$also zu 90°

ABC sei ein Dreieck innerhalb einesKreisesmit${\overline {AB}}$als Kreisdurchmesser und demRadius$r$.Dann ist derMittelpunktM der Strecke${\overline {AB}}$auch derKreismittelpunkt.Die Streckenlängen${\overline {AM}}$,${\overline {BM}}$und${\overline {CM}}$sind also gleich dem Radius$r$.

Die Strecke${\overline {CM}}$teilt das Dreieck$ABC$in zwei Dreiecke$AMC$und$BCM$auf, diegleichschenkligsind. Die Basiswinkel dieser Dreiecke, also dieWinkelan der Grundseite${\overline {AC}}$bzw.${\overline {BC}}$,sind daher jeweils gleich ($\ Alpha$beziehungsweise$\beta$in der Abbildung).

DieWinkelsummeim Dreieck$ABC$beträgt 180°:

$\ Alpha +\beta +\ Alpha +\beta =180^{\circ }$

$2\cdot (\ Alpha +\beta )=180^{\circ }$

Dividiert man dieseGleichungauf beiden Seiten durch 2, so ergibt sich

$\ Alpha +\beta \,=\,90^{\circ }$.

Damit ist gezeigt, dass derWinkel$\ Alpha +\beta$mit Scheitel$C$einrechter Winkelist.

Die Umkehrung des Satzes von Thales lässt sich auf die Aussage zurückführen, dass dieDiagonaleneinesRechtecksgleich lang sind und sich gegenseitig halbieren.

Beweis mit Vervollständigung zum Rechteck

Der Punkt$D$entsteht durchSpiegelungvom Punkt$C$amDurchmesser${\overline {AB}}$und an derMittelsenkrechtenvon${\overline {AB}}$.Das Viereck$ACBD$ist einRechteck.

Wird der Punkt$C$amDurchmesser${\overline {AB}}$und anschließend an derMittelsenkrechtenvon${\overline {AB}}$gespiegelt, dann liegt der Bildpunkt$D$wegenSymmetrieauf dem unterenHalbkreisüber der Seite${\overline {AB}}$.Das ist einePunktspiegelungam Kreismittelpunkt$M$.Daher sind die Seiten und${\overline {AC}}$und${\overline {BD}}$sowie${\overline {AD}}$und${\overline {BC}}$parallelund dasViereck$ACBD$ist einParallelogramm.Weil dieDiagonalen${\overline {AB}}$und${\overline {CD}}$Durchmesser desKreisesund daher gleich lang sind, ist das Parallelogramm ein Rechteck und derWinkelbei$C$einrechter Winkel.

Beweis mit kartesischen Koordinaten

Der Kreismittelpunkt sei derKoordinatenursprung.Sind derRadius$r$und die Punkte$A=(-r,0)$,$B=(r,0)$und$C=(x,y)$mitkartesischen Koordinatengegeben, dann gilt nach demSatz des Pythagoras$x^{2}+y^{2}=r^{2}$.Wegen$(r+x)^{2}+y^{2}={\overline {AC}}^{2}$und$(r-x)^{2}+y^{2}={\overline {BC}}^{2}$gilt imDreieck$ABC$dieGleichung

${\overline {AC}}^{2}+{\overline {BC}}^{2}=((r+x)^{2}+y^{2})+((r-x)^{2}+y^{2})=2r^{2}+2(x^{2}+y^{2})=4r^{2}={\overline {AB}}^{2}$.

Aus der Umkehrung des Satzes des Pythagoras folgt, dass das Dreieck$ABC$im Punkt$C$rechtwinkligist.

Mit demSatz des Pythagoraskann auch gezeigt werden, dass dasSkalarproduktderVektoren${\vec {AC}}$und${\vec {CB}}$gleich Null ist:

Es ist${\vec {AC}}={\binom {x_{C}}{y_{C}}}\ominus {\binom {-r}{0}}={\binom {r+x_{C}}{y_{C}}}$und${\vec {CB}}={\binom {r}{0}}\ominus {\binom {x_{C}}{y_{C}}}={\binom {r-x_{C}}{-y_{C}}}$.

${\vec {AC}}\odot {\vec {CB}}=(r+x_{C})\cdot (r-x_{C})-{y_{C}}^{2}=r^{2}-{x_{C}}^{2}-{y_{C}}^{2}\ {\stackrel {\text{Satz des Pythagoras}}{=}}\ 0={\overline {AC}}\cdot {\overline {CB}}\cdot \cos(\measuredangle ACB)$,

woraus folgt, dass derKosinusdes Winkels im Punkt C gleich Null ist und somit das Dreieck ABC einenrechten Winkelin C hat.

Trigonometrischer Beweis

Sind derWinkel$\beta$,derRadius$r$und die Punkte$A=(-r,0)$,$B=(r,0)$mitkartesischen Koordinatengegeben, dann hat der Punkt$C$dieKoordinaten$C=(r\cdot \cos(\beta ),r\cdot \sin(\beta ))$.Die Seite${\overline {AC}}$hat dieSteigung

${\frac {r\cdot \sin(\beta )-0}{r\cdot \cos(\beta )-(-r)}}={\frac {\sin(\beta )}{\cos(\beta )+1}}$

und die Seite${\overline {BC}}$hat die Steigung

${\frac {r\cdot \sin(\beta )-0}{r\cdot \cos(\beta )-r}}={\frac {\sin(\beta )}{\cos(\beta )-1}}$.

Wegen$\sin ^{2}(\beta )+\cos ^{2}(\beta )=1$ist das Produkt der Steigungen gleich

${\frac {\sin(\beta )}{\cos(\beta )+1}}\cdot {\frac {\sin(\beta )}{\cos(\beta )-1}}={\frac {\sin ^{2}(\beta )}{\cos ^{2}(\beta )-1}}={\frac {\sin ^{2}(\beta )}{-\sin ^{2}(\beta )}}=-1$.

Daraus folgt, dass die Seiten${\overline {AC}}$und${\overline {BC}}$zueinanderorthogonalsind und einenrechten Winkelbilden.

Einen weiteren Beweis findet man hier:Wikibooks: Beweisarchiv.

Anwendungen

Konstruktion einer Kreistangente

Konstruktion derKreistangenten

Eine wichtige Anwendung des Satzes von Thales ist u. a. dieKonstruktionder beidenTangentenan einenKreisk durch einen außerhalb dieses Kreises gelegenenPunkt$P$.

Gegeben sei derRadius$r$vomKreis$k$mit seinemMittelpunkt$O$sowie derAbstanddes Punktes$P$von$O$.Vom Punkt$T$wissen wir nur, dass er auf der Kreislinie, irgendwo im ersten Viertel vom Kreis$k$,liegen muss. Würde man nur diese Bedingung berücksichtigen, könnte man unendlich viele Dreiecke$OPT$einzeichnen.

Da die obere durch$P$verlaufendeTangente$t$den Kreis$k$genau im Punkt$T$berührt, muss das Dreieck$OPT$einen rechten Winkel am Punkt$T$haben (Grundeigenschaft der Kreistangente), oder anders formuliert: Die Strecke${\overline {OT}}$muss senkrecht auf der Tangente$t$stehen.

Um ein Dreieck$OPT$zu finden, das auchrechtwinkligist, ermitteln wir von der Strecke${\overline {OP}}$denMittelpunkt$H$mithilfe derMittelsenkrechten,zeichnen einen Kreis mit demRadius${\overline {HO}}$um den Mittelpunkt$H$und machen uns das Prinzip des Thaleskreises zunutze: Alle Dreiecke mit der Grundseite${\overline {OP}}$,deren dritterEckpunktauf dem Thaleskreis liegt, sind rechtwinklig. Dies gilt natürlich auch für das Dreieck$OPT$.

DerBerührpunkt$T$kann deshalb nur derSchnittpunktdes Kreises$k$mit dem hellgrauen Kreis sein. Durch Verbinden von$P$mit$T$erhält man nun die gesuchte Tangente$t$(in der Zeichnung rot).

Es existiert eine zweite,symmetrischeLösungin der unteren Hälfte desKreises.DieTangente$t'$(ebenfalls rot gezeichnet) berührt den Kreis ebenfalls, und zwar im Punkt$T'$.

Riemengetriebe

→Hauptartikel:Riemengetriebe

Für die zwei folgenden Anwendungen beginnt man mit der Konstruktion der beiden Kreistangenten an den Hilfskreis$k_{3}$(grün) – analog zur obigen Beschreibung – mithilfe des Mittelpunktes$M_{2}$der kleineren Riemenscheibe.

Konstruktionsskizze für Riemengetriebe, gleicheDrehrichtungder Riemenscheiben (blau)
Der Radius$r_{3}$des Hilfskreises$k_{3}$(grün) ergibt sich aus derSubtraktionder beiden Kreisradien:$r_{3}=r_{1}-r_{2}.$

Konstruktionsskizze für gekreuztes Riemengetriebe, umgekehrte Drehrichtung der Riemenscheiben (blau)
Der Radius$r_{3}$des Hilfskreises$k_{3}$(grün) ergibt sich aus derSummeder beiden Kreisradien:$r_{3}=r_{1}+r_{2}.$

Konstruktion reeller Quadratwurzeln

Mithilfe des Satzes des Thales lassen sich die folgendenQuadratwurzelnkonstruieren:

• ${\sqrt {q}}$aus$q>0$und${\sqrt {c}}$aus$c>1$(sieheZahl größer als 1).
• ${\sqrt {p\cdot q}}$aus$c=1,\;{\sqrt {q}}$aus$q<1$und${\sqrt {p}}$aus$p<1$(sieheZahl kleiner als 1).

Zahl größer als 1

Zahl größer als 1: Konstruktion von${\sqrt {q}}$und${\sqrt {c}}$mit Zirkel und Lineal

Soll dieQuadratwurzeleinerreellen Zahl,die größer als 1 ist, gefunden werden, ohne vorherige Aufteilung der Zahl in$p$- und$q$-Anteile, eignet sich dafür die Methode, die das nebenstehende Bild zeigt. ImPrinzipsind damit auch Quadratwurzeln von Zahlen, die kleiner als 1 sind, vorstellbar.

Es beginnt mit dem Einzeichnen der Strecke${\overline {BD}}$mit Länge$p=1$auf einer hier nicht näher bezeichnetenGeraden.Ist die gegebene Zahl$q$eineganze Zahl,wird dasProdukt$q\cdot {\overline {BD}}$ab dem Punkt$D$auf die Gerade abgetragen; d. h. ist z. B. die Zahl$q=8$,wird die Strecke${\overline {BD}}$achtmal abgetragen. Der dadurch entstehende Schnittpunkt$A$bringt dieHypotenuse$c=p+q$des entstehendenDreiecks$ABC$.

Ist$q$einereelle Zahl,besteht u. a. auch die Möglichkeit,$q$mithilfe desdritten Strahlensatzeszukonstruieren.

Es folgen dieSenkrechteauf$c$imPunkt$D$und die Halbierung der Seite$c$in$M$.Abschließend wird der Thaleskreis um$M$gezogen.

• Nach demHöhensatz des Euklidgilt$h^{2}=p\cdot q$,daraus folgt$h^{2}=1\cdot q$,

somit ist die Höhe des rechtwinkligen Dreiecks$ABC$gleich der Quadratwurzel aus$q$.

• Nach demKathetensatz des Euklidgilt$a^{2}=p\cdot c,$daraus folgt$a^{2}=1\cdot c,$

somit ist die Seitenlänge$a$des rechtwinkligen Dreiecks$ABC$gleich der Quadratwurzel aus$c$.

Zahl kleiner als 1

Zahl kleiner als 1: Konstruktion von${\sqrt {p\cdot q}},\;{\sqrt {q}}$und${\sqrt {p}}$mit Zirkel und Lineal

Ist dieQuadratwurzeleiner Zahl, die kleiner als$1$ist, gesucht, eignet sich dafür die Methode, die das nebenstehende Bild zeigt.

Es beginnt ab dem Punkt$A$(Wert$0$) mit einerHalbgeraden.Darauf wird die Strecke${\overline {AB}}$mit Länge$1$und die Strecke${\overline {AE}}$mit Länge$0{,}1$bestimmt. Dabei ergibt sich dieHypotenuse$c$des entstehenden Dreiecks$ABC.$Hat die gegebene Dezimalzahl$q$nureineNachkommastelle,wird das Produkt$q\cdot {\overline {AE}}$ab dem Punkt$A$abgetragen; d. h. ist z. B.$q=0{,}8$wird die Strecke${\overline {AE}}$achtmal abgetragen. Der dadurch entstehendeSchnittpunkt$D$bringt$c=p+q.$

Wenn die gegebene Dezimalzahl$q$mehr als eineNachkommastelle hat, z. B.$q=0{,}86$,besteht u. a. die Möglichkeit, wie bereits oben im AbschnittZahl größer als 1darauf hingewiesen,$q$mithilfe des drittenStrahlensatzeszu konstruieren.

Es folgen dieSenkrechteauf die Strecke${\overline {AB}}$im Punkt$D$und die Halbierung der Seite$c$in$M.$Abschließend wird der Thaleskreis (Radius$=0{,}5$) um$M$gezogen.

• Nach dem Höhensatz des Euklid gilt$h^{2}=p\cdot q,$

somit ist die Höhe$h$des rechtwinkligen Dreiecks$ABC$gleich derQuadratwurzelaus$p\cdot q$.

Wegen$h={\sqrt {p\cdot q}}$gilt auch:

Im rechtwinkligen Dreieck$ABC$ist die Länge$h$dasgeometrische Mittelder Längen$p$und$q$.

• Nach demSatz des Pythagorasgilt für die Seitenlänge$b$:

$b^{2}=q^{2}+p\cdot q$,darin ist$p=1-q$,damit ergibt sich

$b^{2}=q^{2}+q\cdot \left(1-q\right)$

$b^{2}=q^{2}+q-q^{2}\Rightarrow$

$b={\sqrt {q}},$

somit ist die Seitenlänge$b$desrechtwinkligen Dreiecks$ABC$gleich derQuadratwurzelaus$q$.

Für die Seitenlänge$a:$

Mit den entsprechenden Werten für die Seitenlänge$a$ergibt sich

$a={\sqrt {p}},$

somit ist die Seitenlänge$a$des rechtwinkligen Dreiecks$ABC$gleich der Quadratwurzel aus$p.$

Literatur

• Max Koecher,Aloys Krieg:Ebene Geometrie.3., neu bearbeitete und erweiterte Auflage. Springer, Berlin u. a. 2007,ISBN 978-3-540-49327-3.
• Hans Schupp:Elementargeometrie(=Uni-Taschenbücher669). Schöningh, Paderborn 1977,ISBN 3-506-99189-2,S. 41.

Siehe auch

Quadratur des Rechtecks

Weblinks

Commons:Satz des Thales– Sammlung von Bildern, Videos und Audiodateien

• Euklids Beweis (Satz III.31).(PDF; 530 kB) Deutsch von Rudolf Haller.
• Interaktive Grafik zum Verständnis.Walter Fendt