Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

The size of the proton

Nature volume 466, pages 213–216 (2010)Cite this article

Subjects

Abstract

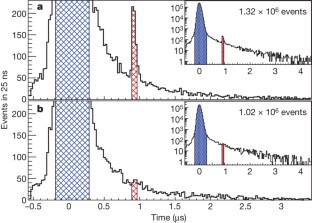
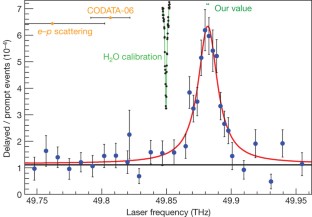
The proton is the primary building block of the visible Universe, but many of its properties—such as its charge radius and its anomalous magnetic moment—are not well understood. The root-mean-square charge radius, rp, has been determined with an accuracy of 2 per cent (at best) by electron–proton scattering experiments1,2. The present most accurate value of rp (with an uncertainty of 1 per cent) is given by the CODATA compilation of physical constants3. This value is based mainly on precision spectroscopy of atomic hydrogen4,5,6,7 and calculations of bound-state quantum electrodynamics (QED; refs 8, 9). The accuracy of rp as deduced from electron–proton scattering limits the testing of bound-state QED in atomic hydrogen as well as the determination of the Rydberg constant (currently the most accurately measured fundamental physical constant3). An attractive means to improve the accuracy in the measurement of rp is provided by muonic hydrogen (a proton orbited by a negative muon); its much smaller Bohr radius compared to ordinary atomic hydrogen causes enhancement of effects related to the finite size of the proton. In particular, the Lamb shift10 (the energy difference between the 2S1/2 and 2P1/2 states) is affected by as much as 2 per cent. Here we use pulsed laser spectroscopy to measure a muonic Lamb shift of 49,881.88(76) GHz. On the basis of present calculations11,12,13,14,15 of fine and hyperfine splittings and QED terms, we find rp = 0.84184(67) fm, which differs by 5.0 standard deviations from the CODATA value3 of 0.8768(69) fm. Our result implies that either the Rydberg constant has to be shifted by −110 kHz/c (4.9 standard deviations), or the calculations of the QED effects in atomic hydrogen or muonic hydrogen atoms are insufficient.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Energy levels, cascade and experimental principle in muonic hydrogen.
Figure 2: Muon beam.
Figure 3: Laser system.
Figure 4: Summed X-ray time spectra.
Figure 5: Resonance.

Similar content being viewed by others

References

  1. Sick, I. On the rms-radius of the proton. Phys. Lett. B 576, 62–67 (2003)

    Article  ADS  CAS  Google Scholar 

  2. Blunden, P. G. & Sick, I. Proton radii and two-photon exchange. Phys. Rev. C 72, 057601 (2005)

    Article  ADS  Google Scholar 

  3. Mohr, P. J., Taylor, B. N. & Newell, D. B. CODATA recommended values of the fundamental physical constants: 2006. Rev. Mod. Phys. 80, 633–730 (2008)

    Article  ADS  CAS  Google Scholar 

  4. Niering, M. et al. Measurement of the hydrogen 1S - 2S transition frequency by phase coherent comparison with a microwave cesium fountain clock. Phys. Rev. Lett. 84, 5496–5499 (2000)

    Article  ADS  CAS  Google Scholar 

  5. Fischer, M. et al. New limits on the drift of fundamental constants from laboratory measurements. Phys. Rev. Lett. 92, 230802 (2004)

    Article  ADS  CAS  Google Scholar 

  6. de Beauvoir, B. et al. Metrology of the hydrogen and deuterium atoms: determination of the Rydberg constant and Lamb shifts. Eur. Phys. J. D 12, 61–93 (2000)

    Article  ADS  CAS  Google Scholar 

  7. Schwob, C. et al. Optical frequency measurement of the 2S – 12D transitions in hydrogen and deuterium: Rydberg constant and Lamb shift determinations. Phys. Rev. Lett. 82, 4960–4963 (1999)

    Article  ADS  CAS  Google Scholar 

  8. Eides, M. I., Grotch, H. & Shelyuto, V. A. Theory of light hydrogenlike atoms. Phys. Rep. 342, 63–261 (2001)

    Article  ADS  CAS  Google Scholar 

  9. Karshenboim, S. G. Precision physics of simple atoms: QED tests, nuclear structure and fundamental constants. Phys. Rep. 422, 1–63 (2005)

    Article  ADS  Google Scholar 

  10. Lamb, W. E. & Retherford, R. C. Fine structure of the hydrogen atom by a microwave method. Phys. Rev. 72, 241–243 (1947)

    Article  ADS  CAS  Google Scholar 

  11. Pachucki, K. Theory of the Lamb shift in muonic hydrogen. Phys. Rev. A 53, 2092–2100 (1996)

    Article  ADS  CAS  Google Scholar 

  12. Pachucki, K. Proton structure effects in muonic hydrogen. Phys. Rev. A 60, 3593–3598 (1999)

    Article  ADS  CAS  Google Scholar 

  13. Borie, E. Lamb shift in muonic hydrogen. Phys. Rev. A 71, 032508 (2005)

    Article  ADS  Google Scholar 

  14. Martynenko, A. P. 2S Hyperfine splitting of muonic hydrogen. Phys. Rev. A 71, 022506 (2005)

    Article  ADS  Google Scholar 

  15. Martynenko, A. P. Fine and hyperfine structure of P-wave levels in muonic hydrogen. Phys. At. Nucl. 71, 125–135 (2008)

    Article  CAS  Google Scholar 

  16. Pachucki, K. & Jentschura, U. D. Two-loop Bethe-logarithm correction in hydrogenlike atoms. Phys. Rev. Lett. 91, 113005 (2003)

    Article  ADS  Google Scholar 

  17. Antognini, A. et al. The 2S Lamb shift in muonic hydrogen and the proton rms charge radius. AIP Conf. Proc. 796, 253–259 (2005)

    Article  ADS  CAS  Google Scholar 

  18. Jensen, T. S. & Markushin, V. E. Collisional deexcitation of exotic hydrogen atoms in highly excited states. Eur. Phys. J. D 21, 261–270 (2002)

    Article  ADS  CAS  Google Scholar 

  19. Pohl, R. 2S state and Lamb shift in muonic hydrogen. Hyp. Interact. 193, 115–120 (2009)

    Article  ADS  CAS  Google Scholar 

  20. Pohl, R. et al. Observation of long-lived muonic hydrogen in the 2S state. Phys. Rev. Lett. 97, 193402 (2006)

    Article  ADS  Google Scholar 

  21. Pohl, R. et al. The muonic hydrogen Lamb-shift experiment. Can. J. Phys. 83, 339–349 (2005)

    Article  ADS  CAS  Google Scholar 

  22. Antognini, A. et al. Thin-disk Yb:YAG oscillator-amplifier laser, ASE, and effective Yb:YAG lifetime. IEEE J. Quantum Electron. 45, 993–1005 (2009)

    Article  ADS  CAS  Google Scholar 

  23. Giesen, A. et al. Scalable concept for diode-pumped high-power solid-state lasers. Appl. Phys. B 58, 365–372 (1994)

    Article  ADS  Google Scholar 

  24. Antognini, A. et al. Powerful fast triggerable 6 µm laser for the muonic hydrogen 2S-Lamb shift experiment. Opt. Commun. 253, 362–374 (2005)

    Article  ADS  CAS  Google Scholar 

  25. Nebel, T. et al. Status of the muonic hydrogen Lamb-shift experiment. Can. J. Phys. 85, 469–478 (2007)

    Article  ADS  CAS  Google Scholar 

  26. Rabinowitz, P., Perry, B. & Levinos, N. A continuously tunable sequential Stokes Raman laser. IEEE J. Quantum Electron. 22, 797–802 (1986)

    Article  ADS  Google Scholar 

  27. Ludhova, L. et al. Planar LAAPDs: temperature dependence, performance, and application in low-energy x-ray spectroscopy. Nucl. Instrum. Methods A 540, 169–179 (2005)

    Article  ADS  CAS  Google Scholar 

  28. Toth, R. A. Water vapor measurements between 590 and 2582 cm−1: Line positions and strengths. J. Mol. Spectrosc. 190, 379–396 (1998)

    Article  ADS  CAS  Google Scholar 

  29. Rothman, L. S. et al. The HITRAN 2008 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 110, 533–572 (2009)

    Article  ADS  CAS  Google Scholar 

  30. Kilic, S., Karr, J.-P. & Hilico, L. Coulombic and radiative decay rates of the resonances of the exotic molecular ions ppµ, ppπ, ddµ, ddπ, and dtµ. Phys. Rev. A 70, 042506 (2004)

    Article  ADS  Google Scholar 

  31. Lundeen, S. R. & Pipkin, F. M. Measurement of the Lamb shift in hydrogen, n = 2. Phys. Rev. Lett. 46, 232–235 (1981)

    Article  ADS  CAS  Google Scholar 

  32. Belushkin, M. A., Hammer, H.-W. & Meissner, U.-G. Dispersion analysis of the nucleon form factors including meson continua. Phys. Rev. C 75, 035202 (2007)

    Article  ADS  Google Scholar 

  33. Hanneke, D., Fogwell, S. & Gabrielse, G. New measurement of the electron magnetic moment and the fine structure constant. Phys. Rev. Lett. 100, 120801 (2008)

    Article  ADS  CAS  Google Scholar 

Download references

Acknowledgements

We thank L. Simons and B. Leoni for setting up the cyclotron trap, H. Brückner, K. Linner, W. Simon, O. Huot and Z. Hochman for technical support, P. Maier-Komor, K. Nacke, M. Horisberger, A. Weber, L. Meier and J. Hehner for thin foils and windows, N. Schlumpf, U. Hartmann and M. Gaspar for electronics, S. Spielmann-Jaeggi and L. Carroll for optical measurements, Ch. Parthey and M. Herrmann for their help, the MEG-collaboration for a share of beam-time, and A. Voss, B. Weichelt and J. Fruechtenicht for the loan of a laser pump diode. We acknowledge the essential contributions of H. Hofer and V.W. Hughes in the initial stages of the experiment. We also thank the PSI accelerator division, the Hallendienst, the workshops at PSI, MPQ and Fribourg, and other support groups for their help. We acknowledge support from the Max Planck Society and the Max Planck Foundation, the Swiss National Science Foundation (project 200020-100632) and the Swiss Academy of Engineering Sciences, the BQR de l'UFR de physique fondamentale et appliquée de l'Université Paris 6, the program PAI Germaine de Staël no. 07819NH du ministère des affaires étrangères France, and the Fundação para a Ciência e a Tecnologia (Portugal) and FEDER (project PTDC/FIS/82006/2006 and grant SFRH/BPD/46611/2008). P.I. and E.-O.L.B. acknowledge support from the ‘ExtreMe Matter Institute, Helmholtz Alliance HA216/EMMI’.

Author information

Author notes

  1. Adolf Giesen & Françoise Mulhauser

    Present address: Present addresses: Deutsches Zentrum für Luft- und Raumfahrt e.V. in der Helmholtz-Gemeinschaft, 70569 Stuttgart, Germany (A.G.); International Atomic Energy Agency, A-1400 Vienna, Austria (F.M.).,

Authors and Affiliations

  1. Max-Planck-Institut für Quantenoptik, Garching, 85748, Germany

    Randolf Pohl, Aldo Antognini, Theodor W. Hänsch & Tobias Nebel

  2. Laboratoire Kastler Brossel, École Normale Supérieure, CNRS, and Université P. et M. Curie-Paris 6, 75252 Paris, Cedex 05, France,

    François Nez, François Biraben, Paul Indelicato, Lucile Julien, Eric-Olivier Le Bigot & Catherine Schwob

  3. Departamento de Física, Universidade de Coimbra, Coimbra, 3004-516, Portugal

    Fernando D. Amaro, João M. R. Cardoso, Daniel S. Covita, Luis M. P. Fernandes, José A. M. Lopes, Cristina M. B. Monteiro & Joaquim M. F. dos Santos

  4. Departamento de Física, I3N, Universidade de Aveiro, Aveiro, 3810-193, Portugal

    Daniel S. Covita & João F. C. A. Veloso

  5. Physics Department, Yale University, New Haven, 06520-8121, Connecticut, USA

    Andreas Dax & Satish Dhawan

  6. Institut für Strahlwerkzeuge, Universität Stuttgart, Stuttgart, 70569, Germany

    Adolf Giesen & Thomas Graf

  7. Physics Department, National Tsing Hua University, Hsinchu, 300, Taiwan

    Cheng-Yang Kao & Yi-Wei Liu

  8. Département de Physique, Université de Fribourg, Fribourg, 1700, Switzerland

    Paul Knowles, Livia Ludhova, Françoise Mulhauser & Lukas A. Schaller

  9. Department of Chemistry, Princeton University, Princeton, 08544-1009, New Jersey, USA

    Paul Rabinowitz

  10. Dausinger & Giesen GmbH, Rotebühlstr. 87, 70178 Stuttgart, Germany,

    Karsten Schuhmann

  11. Paul Scherrer Institute, Villigen-PSI, 5232, Switzerland

    David Taqqu

  12. Institut für Teilchenphysik, ETH Zürich, 8093 Zürich, Switzerland,

    Franz Kottmann

Authors
  1. Randolf Pohl
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aldo Antognini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. François Nez
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fernando D. Amaro
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. François Biraben
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. João M. R. Cardoso
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Daniel S. Covita
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Andreas Dax
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Satish Dhawan
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Luis M. P. Fernandes
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Adolf Giesen
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Thomas Graf
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Theodor W. Hänsch
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Paul Indelicato
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Lucile Julien
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. Cheng-Yang Kao
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Paul Knowles
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. Eric-Olivier Le Bigot
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. Yi-Wei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  20. José A. M. Lopes
    View author publications

    You can also search for this author in PubMed Google Scholar

  21. Livia Ludhova
    View author publications

    You can also search for this author in PubMed Google Scholar

  22. Cristina M. B. Monteiro
    View author publications

    You can also search for this author in PubMed Google Scholar

  23. Françoise Mulhauser
    View author publications

    You can also search for this author in PubMed Google Scholar

  24. Tobias Nebel
    View author publications

    You can also search for this author in PubMed Google Scholar

  25. Paul Rabinowitz
    View author publications

    You can also search for this author in PubMed Google Scholar

  26. Joaquim M. F. dos Santos
    View author publications

    You can also search for this author in PubMed Google Scholar

  27. Lukas A. Schaller
    View author publications

    You can also search for this author in PubMed Google Scholar

  28. Karsten Schuhmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  29. Catherine Schwob
    View author publications

    You can also search for this author in PubMed Google Scholar

  30. David Taqqu
    View author publications

    You can also search for this author in PubMed Google Scholar

  31. João F. C. A. Veloso
    View author publications

    You can also search for this author in PubMed Google Scholar

  32. Franz Kottmann
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

R.P., A.A., F.N., F.D.A., F.B., A.D., A.G., T.G., T.W.H., L.J., C.-Y.K., Y.-W.L., T.N., P.R., K.S., C.S. and F.K. designed, built and operated parts of the laser system. R.P., A.A., F.N., D.S.C., L.M.P.F., P.K., Y.-W.L., J.A.M.L., L.L., C.M.B.M., F.M., T.N., J.M.F.d.S., L.A.S., K.S., D.T., J.F.C.A.V. and F.K. planned, built and set up the various detectors of the experiment. R.P., A.A., D.S.C., F.M., D.T., J.F.C.A.V. and F.K. designed, built, set up and operated the muon beam line. R.P., A.A., F.N., J.M.R.C., D.S.C., A.D., S.D., L.M.P.F., C.-Y.K., P.K., Y.-W.L., F.M., T.N., J.M.F.d.S., K.S., D.T., J.F.C.A.V. and F.K. designed and implemented the electronics used in the experiment. R.P., A.A., J.M.R.C., P.I., P.K., E.-O.L.B. and T.N. set up the computing infrastructure, wrote software and realized the data acquisition system. R.P., A.A., F.N., F.D.A. F.B., J.M.R.C., D.S.C., A.D., L.M.P.F., P.I., L.J., C.-Y.K., P.K., E.-O.L.B., Y.-W.L., J.A.M.L., L.L., C.M.B.M., F.M., T.N., J.M.F.d.S., K.S., C.S., D.T., J.F.C.A.V. and F.K. took part in the months-long data-taking runs. E.-O.L.B., P.I. and F.K. did work on QED theory. R.P., A.A., F.N., F.B., P.I., L.J., P.K., L.L., T.N., D.T. and F.K. analysed the data and wrote the initial manuscript. The manuscript was then read, improved and finally approved by all authors.

Corresponding author

Correspondence to Randolf Pohl.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

This file contains Supplementary Data, References and Supplementary Tables 1-2. (PDF 92 kb)

PowerPoint slides

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pohl, R., Antognini, A., Nez, F. et al. The size of the proton. Nature 466, 213–216 (2010). https://doi.org/10.1038/nature09250

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature09250

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing