Antimatroid

Inmathematics,anantimatroidis aformal systemthat describes processes in which asetis built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included.Antimatroids are commonlyaxiomatized in two equivalent ways,either as aset systemmodeling the possible states of such a process, or as aformal languagemodeling the different sequences in which elements may be included. Dilworth(1940) was the first to study antimatroids, using yet another axiomatization based onlattice theory,and they have been frequently rediscovered in other contexts.

Three views of an antimatroid: an inclusion ordering on its family of feasible sets, a formal language, and the corresponding path poset.

The axioms defining antimatroids as set systems are very similar to those ofmatroids,but whereas matroids are defined by anexchange axiom,antimatroids are defined instead by ananti-exchange axiom,from which their name derives. Antimatroids can be viewed as a special case ofgreedoidsand ofsemimodular lattices,and as a generalization ofpartial ordersand ofdistributive lattices. Antimatroids are equivalent, bycomplementation,toconvex geometries,a combinatorial abstraction ofconvex setsingeometry.

Antimatroids have been applied to model precedence constraints inscheduling problems,potential event sequences in simulations, task planning inartificial intelligence,and the states of knowledge of human learners.

Definitions

An antimatroid can be defined as a finite family${\mathcal {F}}$of finite sets, calledfeasible sets,with the following two properties:

• Theunionof any two feasible sets is also feasible. That is,${\mathcal {F}}$isclosedunder unions.
• If$S$is a nonempty feasible set, then$S$contains an element$x$for which$S\setminus \{x\}$(the set formed by removing$x$from$S$) is also feasible. That is,${\mathcal {F}}$is anaccessible set system.

Antimatroids also have an equivalent definition as aformal language,that is, as a set ofstringsdefined from a finite alphabet ofsymbols.A string that belongs to this set is called awordof the language. A language${\mathcal {L}}$defining an antimatroid must satisfy the following properties:

• Every symbol of the alphabet occurs in at least one word of${\mathcal {L}}$.
• Each word of${\mathcal {L}}$contains at most one copy of each symbol. A language with this property is callednormal.
• Everyprefixof a word in${\mathcal {L}}$is also in${\mathcal {L}}$.A language with this property is calledhereditary.
• If$S$and$T$are words in${\mathcal {L}}$,and$S$contains at least one symbol that is not in$T$,then there is a symbol$x$in$S$such that theconcatenation$Tx$is another word in${\mathcal {L}}$.

The equivalence of these two forms of definition can be seen as follows. If${\mathcal {L}}$is an antimatroid defined as a formal language, then the sets of symbols in words of${\mathcal {L}}$form an accessible union-closed set system. It is accessible by the hereditary property of strings, and it can be shown to be union-closed by repeated application of the concatenation property of strings. In the other direction, from an accessible union-closed set system${\mathcal {F}}$,the language of normal strings whose prefixes all have sets of symbols belonging to${\mathcal {F}}$meets the requirements for a formal language to be an antimatroid. These two transformations are the inverses of each other: transforming a formal language into a set family and back, or vice versa, produces the same system. Thus, these two definitions lead to mathematically equivalent classes of objects.

Examples

A shelling sequence of a planar point set. The line segments show edges of theconvex hullsafter some of the points have been removed.

The following systems provide examples of antimatroids:

Chain antimatroids

The prefixes of a single string, and the sets of symbols in these prefixes, form an antimatroid. For instance the chain antimatroid defined by the string$abcd$has as its formal language the set of strings$$\{\varepsilon,a,ab,abc,abcd\}$$(where$\varepsilon$denotes theempty string) and as its family of feasible sets the family$${\bigl \{}\emptyset,\{a\},\{a,b\},\{a,b,c\},\{a,b,c,d\}{\bigr \}}.$$

Poset antimatroids

Thelower setsof a finitepartially ordered setform an antimatroid, with the full-length words of the antimatroid forming thelinear extensionsof the partial order.ByBirkhoff's representation theoremfor distributive lattices, the feasible sets in a poset antimatroid (ordered by set inclusion) form a distributive lattice, and all distributive lattices can be formed in this way. Thus, antimatroids can be seen as generalizations of distributive lattices. A chain antimatroid is the special case of a poset antimatroid for atotal order.

Shelling antimatroids

Ashelling sequenceof a finite set$U$of points in theEuclidean planeor a higher-dimensionalEuclidean spaceis formed by repeatedly removing vertices of theconvex hull.The feasible sets of the antimatroid formed by these sequences are theintersectionsof$U$with thecomplementof a convex set.

Perfect elimination

Aperfect elimination orderingof achordal graphis an ordering of its vertices such that, for each vertex$v$,the neighbors of$v$that occur later than$v$in the ordering form aclique.The prefixes of perfect elimination orderings of a chordal graph form an antimatroid.

Chip-firing games

Chip-firing gamessuch as theabelian sandpile modelare defined by adirected graphtogether with a system of "chips" placed on its vertices. Whenever the number of chips on a vertex$v$is at least as large as the number of edges out of$v$,it is possible tofire$v$,moving one chip to each neighboring vertex. The event that$v$fires for the$i$th time can only happen if it has already fired$i-1$times and accumulated$i\cdot \deg(v)$total chips. These conditions do not depend on the ordering of previous firings, and remain true until$v$fires, so any given graph and initial placement of chips for which the system terminates defines an antimatroid on the pairs$(v,i)$.A consequence of the antimatroid property of these systems is that, for a given initial state, the number of times each vertex fires and the eventual stable state of the system do not depend on the firing order.

Paths and basic words

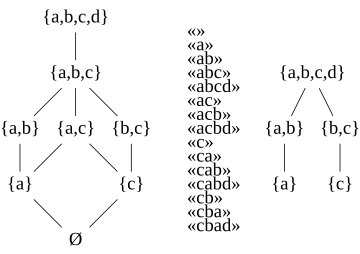
In the set theoretic axiomatization of an antimatroid there are certain special sets calledpathsthat determine the whole antimatroid, in the sense that the sets of the antimatroid are exactly the unions of paths.If$S$is any feasible set of the antimatroid, an element$x$that can be removed from$S$to form another feasible set is called anendpointof$S$,and a feasible set that has only one endpoint is called apathof the antimatroid.The family of paths can be partially ordered by set inclusion, forming thepath posetof the antimatroid.

For every feasible set$S$in the antimatroid, and every element$x$of$S$,one may find a path subset of$S$for which$x$is an endpoint: to do so, remove one at a time elements other than$x$until no such removal leaves a feasible subset. Therefore, each feasible set in an antimatroid is the union of its path subsets.If$S$is not a path, each subset in this union is aproper subsetof$S$.But, if$S$is itself a path with endpoint$x$,each proper subset of$S$that belongs to the antimatroid excludes$x$.Therefore, the paths of an antimatroid are exactly the feasible sets that do not equal the unions of their proper feasible subsets. Equivalently, a given family of sets${\mathcal {P}}$forms the family of paths of an antimatroid if and only if, for each$S$in${\mathcal {P}}$,the union of subsets of$S$in${\mathcal {P}}$has one fewer element than$S$itself.If so,${\mathcal {F}}$itself is the family of unions of subsets of${\mathcal {P}}$.

In the formal language formalization of an antimatroid, the longest strings are calledbasic words.Each basic word forms a permutation of the whole alphabet.If$B$is the set of basic words,${\mathcal {L}}$can be defined from$B$as the set of prefixes of words in$B$.

Convex geometries

See also:Convex set,Convex geometry,andClosure operator

If${\mathcal {F}}$is the set system defining an antimatroid, with$U$equal to the union of the sets in${\mathcal {F}}$,then the family of sets $${\mathcal {G}}=\{U\setminus S\mid S\in {\mathcal {F}}\}$$ complementaryto the sets in${\mathcal {F}}$is sometimes called aconvex geometryand the sets in${\mathcal {G}}$are calledconvex sets.For instance, in a shelling antimatroid, the convex sets are intersections of the given point set with convex subsets of Euclidean space. The set system defining a convex geometry must be closed under intersections. For any set$S$in${\mathcal {G}}$that is not equal to$U$there must be an element$x$not in$S$that can be added to$S$to form another set in${\mathcal {G}}$.

A convex geometry can also be defined in terms of aclosure operator$\tau$that maps any subset of$U$to its minimal closed superset. To be a closure operator,$\tau$should have the following properties:

• $\tau (\emptyset )=\emptyset$:the closure of theempty setis empty.
• For every subset$S$of$U$,$S$is a subset of$\tau (S)$and$\tau (S)=\tau {\bigl (}\tau (S){\bigr )}$.
• Whenever$S\subset T\subset U$,$\tau (S)$is a subset of$\tau (T)$.

The family of closed sets resulting from a closure operation of this type is necessarily closed under intersections, but might not be a convex geometry. The closure operators that define convex geometries also satisfy an additionalanti-exchange axiom:

• If$S$is a subset of$U$,and$y$and$z$are distinct elements of$U$that do not belong to$\tau (S)$,but$z$does belong to$\tau (S\cup \{y\})$,then$y$does not belong to$\tau (S\cup \{z\})$.

A closure operation satisfying this axiom is called ananti-exchange closure.If$S$is a closed set in an anti-exchange closure, then the anti-exchange axiom determines a partial order on the elements not belonging to$S$,where$x\leq y$in the partial order when$x$belongs to$\tau (S\cup \{y\})$.If$x$is a minimal element of this partial order, then$S\cup \{x\}$is closed. That is, the family of closed sets of an anti-exchange closure has the property that for any set other than the universal set there is an element$x$that can be added to it to produce another closed set. This property is complementary to the accessibility property of antimatroids, and the fact that intersections of closed sets are closed is complementary to the property that unions of feasible sets in an antimatroid are feasible. Therefore, the complements of the closed sets of any anti-exchange closure form an antimatroid.

Theundirected graphsin which the convex sets (subsets of vertices that contain allshortest pathsbetween vertices in the subset) form a convex geometry are exactly thePtolemaic graphs.

Join-distributive lattices

Every two feasible sets of an antimatroid have a uniqueleast upper bound(their union) and a uniquegreatest lower bound(the union of the sets in the antimatroid that are contained in both of them). Therefore, the feasible sets of an antimatroid,partially orderedby set inclusion, form alattice.Various important features of an antimatroid can be interpreted in lattice-theoretic terms; for instance the paths of an antimatroid are thejoin-irreducibleelements of the corresponding lattice, and the basic words of the antimatroid correspond tomaximal chainsin the lattice. The lattices that arise from antimatroids in this way generalize the finitedistributive lattices,and can be characterized in several different ways.

• The description originally considered byDilworth (1940)concernsmeet-irreducibleelements of the lattice. For each element$x$of an antimatroid, there exists a unique maximal feasible set$S_{x}$that does not contain$x$:$S_{x}$can be constructed as the union of all feasible sets not containing$x$.This set$S_{x}$is automatically meet-irreducible, meaning that it is not the meet of any two larger lattice elements. This is true because every feasible superset of$S_{x}$contains$x$,and the same is therefore also true of every intersection of feasible supersets. Every element of an arbitrary lattice can be decomposed as a meet of meet-irreducible sets, often in multiple ways, but in the lattice corresponding to an antimatroid each element$T$has a unique minimal family of meet-irreducible sets whose meet is$T$;this family consists of the sets$S_{x}$for the elements$x$such that$T\cup \{x\}$is feasible. That is, the lattice hasunique meet-irreducible decompositions.
• A second characterization concerns theintervalsin the lattice, the sublattices defined by a pair of lattice elements$x\leq y$consisting of all lattice elements$z$with$x\leq z\leq y$.An interval isatomisticif every element in it is the join of atoms (the minimal elements above the bottom element$x$), and it isBooleanif it is isomorphic to the lattice ofall subsetsof a finite set. For an antimatroid, every interval that is atomistic is also boolean.
• Thirdly, the lattices arising from antimatroids aresemimodular lattices,lattices that satisfy theupper semimodular lawthat for every two elements$x$and$y$,if$y$covers$x\wedge y$then$x\vee y$covers$x$.Translating this condition into the feasible sets of an antimatroid, if a feasible set$Y$has only one element not belonging to another feasible set$X$then that one element may be added to$X$to form another set in the antimatroid. Additionally, the lattice of an antimatroid has themeet-semidistributive property:for all lattice elements$x$,$y$,and$z$,if$x\wedge y$and$x\wedge z$equal each other then they also both equal$x\wedge (y\vee z)$.A semimodular and meet-semidistributive lattice is called ajoin-distributive lattice.

These three characterizations are equivalent: any lattice with unique meet-irreducible decompositions has boolean atomistic intervals and is join-distributive, any lattice with boolean atomistic intervals has unique meet-irreducible decompositions and is join-distributive, and any join-distributive lattice has unique meet-irreducible decompositions and boolean atomistic intervals.Thus, we may refer to a lattice with any of these three properties as join-distributive. Any antimatroid gives rise to a finite join-distributive lattice, and any finite join-distributive lattice comes from an antimatroid in this way.Another equivalent characterization of finite join-distributive lattices is that they aregraded(any two maximal chains have the same length), and the length of a maximal chain equals the number of meet-irreducible elements of the lattice.The antimatroid representing a finite join-distributive lattice can be recovered from the lattice: the elements of the antimatroid can be taken to be the meet-irreducible elements of the lattice, and the feasible set corresponding to any element$x$of the lattice consists of the set of meet-irreducible elements$y$such that$y$is not greater than or equal to$x$in the lattice.

This representation of any finite join-distributive lattice as an accessible family of sets closed under unions (that is, as an antimatroid) may be viewed as an analogue ofBirkhoff's representation theoremunder which any finite distributive lattice has a representation as a family of sets closed under unions and intersections.

Supersolvable antimatroids

Motivated by a problem of defining partial orders on the elements of aCoxeter group,Armstrong (2009)studied antimatroids which are alsosupersolvable lattices.A supersolvable antimatroid is defined by atotally orderedcollection of elements, and afamily of setsof these elements. The family must include the empty set. Additionally, it must have the property that if two sets$A$and$B$belong to the family, if theset-theoretic difference$B\setminus A$is nonempty, and if$x$is the smallest element of$B\setminus A$,then$A\cup \{x\}$also belongs to the family. As Armstrong observes, any family of sets of this type forms an antimatroid. Armstrong also provides a lattice-theoretic characterization of the antimatroids that this construction can form.

Join operation and convex dimension

If${\mathcal {A}}$and${\mathcal {B}}$are two antimatroids, both described as a family of sets over the same universe of elements, then another antimatroid, thejoinof${\mathcal {A}}$and${\mathcal {B}}$,can be formed as follows: $${\mathcal {A}}\vee {\mathcal {B}}=\{S\cup T\mid S\in {\mathcal {A}}\wedge T\in {\mathcal {B}}\}.$$ This is a different operation than the join considered in the lattice-theoretic characterizations of antimatroids: it combines two antimatroids to form another antimatroid, rather than combining two sets in an antimatroid to form another set. The family of all antimatroids over the same universe forms asemilatticewith this join operation.

Joins are closely related to a closure operation that maps formal languages to antimatroids, where the closure of a language${\mathcal {L}}$is the intersection of all antimatroids containing${\mathcal {L}}$as a sublanguage. This closure has as its feasible sets the unions of prefixes of strings in${\mathcal {L}}$.In terms of this closure operation, the join is the closure of the union of the languages of${\mathcal {A}}$and${\mathcal {B}}$.Every antimatroid can be represented as a join of a family of chain antimatroids, or equivalently as the closure of a set of basic words; theconvex dimensionof an antimatroid${\mathcal {A}}$is the minimum number of chain antimatroids (or equivalently the minimum number of basic words) in such a representation. If${\mathfrak {F}}$is a family of chain antimatroids whose basic words all belong to${\mathcal {A}}$,then${\mathfrak {F}}$generates${\mathcal {A}}$if and only if the feasible sets of${\mathfrak {F}}$include all paths of${\mathcal {A}}$.The paths of${\mathcal {A}}$belonging to a single chain antimatroid must form achainin the path poset of${\mathcal {A}}$,so the convex dimension of an antimatroid equals the minimum number of chains needed to cover the path poset, which byDilworth's theoremequals the width of the path poset.

If one has a representation of an antimatroid as the closure of a set of$d$basic words, then this representation can be used to map the feasible sets of the antimatroid to points in$d$-dimensional Euclidean space: assign one coordinate per basic word$W$,and make the coordinate value of a feasible set$S$be the length of the longest prefix of$W$that is a subset of$S$.With this embedding,$S$is a subset of another feasible set$T$if and only if the coordinates for$S$are all less than or equal to the corresponding coordinates of$T$.Therefore, theorder dimensionof the inclusion ordering of the feasible sets is at most equal to the convex dimension of the antimatroid.However, in general these two dimensions may be very different: there exist antimatroids with order dimension three but with arbitrarily large convex dimension.

Enumeration

The number of possible antimatroids on a set of elements grows rapidly with the number of elements in the set. For sets of one, two, three, etc. elements, the number of distinct antimatroids is $$1,3,22,485,59386,133059751,\dots \,.$$

Applications

Both the precedence and release time constraints in the standardnotation for theoretic scheduling problemsmay be modeled by antimatroids.Boyd & Faigle (1990)use antimatroids to generalize agreedy algorithmofEugene Lawlerfor optimally solving single-processor scheduling problems with precedence constraints in which the goal is to minimize the maximum penalty incurred by the late scheduling of a task.

Glasserman & Yao (1994)use antimatroids to model the ordering of events indiscrete event simulationsystems.

Parmar (2003)uses antimatroids to model progress towards a goal inartificial intelligenceplanningproblems.

InOptimality Theory,a mathematical model for the development ofnatural languagebased on optimization under constraints, grammars are logically equivalent to antimatroids.

Inmathematical psychology,antimatroids have been used to describefeasible states of knowledgeof a human learner. Each element of the antimatroid represents a concept that is to be understood by the learner, or a class of problems that he or she might be able to solve correctly, and the sets of elements that form the antimatroid represent possible sets of concepts that could be understood by a single person. The axioms defining an antimatroid may be phrased informally as stating that learning one concept can never prevent the learner from learning another concept, and that any feasible state of knowledge can be reached by learning a single concept at a time. The task of a knowledge assessment system is to infer the set of concepts known by a given learner by analyzing his or her responses to a small and well-chosen set of problems. In this context antimatroids have also been called "learning spaces" and "well-graded knowledge spaces".

References

• Adaricheva, K. V.; Gorbunov, V. A.; Tumanov, V. I. (2003), "Join-semidistributive lattices and convex geometries",Advances in Mathematics,173(1): 1–49,doi:10.1016/S0001-8708(02)00011-7.
• Armstrong, Drew (2009), "The sorting order on a Coxeter group",Journal of Combinatorial Theory,Series A,116(8): 1285–1305,arXiv:0712.1047,doi:10.1016/j.jcta.2009.03.009,MR2568800,S2CID15474840.
• Birkhoff, Garrett;Bennett, M. K. (1985),"The convexity lattice of a poset",Order,2(3): 223–242,doi:10.1007/BF00333128,S2CID118907732
• Björner, Anders;Lovász, László;Shor, Peter W.(1991), "Chip-firing games on graphs",European Journal of Combinatorics,12(4): 283–291,doi:10.1016/S0195-6698(13)80111-4,MR1120415
• Björner, Anders;Ziegler, Günter M.(1992),"Introduction to greedoids",in White, Neil (ed.),Matroid Applications,Encyclopedia of Mathematics and its Applications, vol. 40, Cambridge: Cambridge University Press, pp.284–357,doi:10.1017/CBO9780511662041.009,ISBN0-521-38165-7,MR1165537
• Boyd, E. Andrew; Faigle, Ulrich (1990),"An algorithmic characterization of antimatroids",Discrete Applied Mathematics,28(3): 197–205,doi:10.1016/0166-218X(90)90002-T,hdl:1911/101636.
• Chandran, L. S.; Ibarra, L.;Ruskey, F.;Sawada, J. (2003),"Generating and characterizing the perfect elimination orderings of a chordal graph"(PDF),Theoretical Computer Science,307(2): 303–317,doi:10.1016/S0304-3975(03)00221-4
• Dilworth, Robert P.(1940), "Lattices with unique irreducible decompositions",Annals of Mathematics,41(4): 771–777,doi:10.2307/1968857,JSTOR1968857.
• Doignon, Jean-Paul;Falmagne, Jean-Claude(1999),Knowledge Spaces,Springer-Verlag,ISBN3-540-64501-2.
• Edelman, Paul H. (1980), "Meet-distributive lattices and the anti-exchange closure",Algebra Universalis,10(1): 290–299,doi:10.1007/BF02482912,S2CID120403229.
• Edelman, Paul H.;Saks, Michael E.(1988), "Combinatorial representation and convex dimension of convex geometries",Order,5(1): 23–32,doi:10.1007/BF00143895,S2CID119826035.
• Eppstein, David(2008),Learning sequences,arXiv:0803.4030.Partially adapted as Chapters 13 and 14 ofFalmagne, Jean-Claude;Albert, Dietrich; Doble, Chris;Eppstein, David;Hu, Xiangen, eds. (2013),Knowledge Spaces: Applications in Education,Springer-Verlag,doi:10.1007/978-3-642-35329-1,ISBN978-3-642-35328-4.
• Farber, Martin; Jamison, Robert E. (1986), "Convexity in graphs and hypergraphs",SIAM Journal on Algebraic and Discrete Methods,7(3): 433–444,doi:10.1137/0607049,hdl:10338.dmlcz/127659,MR0844046.
• Glasserman, Paul; Yao, David D. (1994),Monotone Structure in Discrete Event Systems,Wiley Series in Probability and Statistics, Wiley Interscience,ISBN978-0-471-58041-6.
• Gordon, Gary (1997), "A β invariant for greedoids and antimatroids",Electronic Journal of Combinatorics,4(1): Research Paper 13,doi:10.37236/1298,MR1445628.
• Jamison, Robert (1980), "Copoints in antimatroids",Proceedings of the Eleventh Southeastern Conference on Combinatorics, Graph Theory and Computing (Florida Atlantic Univ., Boca Raton, Fla., 1980), Vol. II,Congressus Numerantium, vol. 29, pp. 535–544,MR0608454.
• Kempner, Yulia; Levit, Vadim E. (2003),"Correspondence between two antimatroid algorithmic characterizations",Electronic Journal of Combinatorics,10:Research Paper 44,arXiv:math/0307013,Bibcode:2003math......7013K,doi:10.37236/1737,MR2014531,S2CID11015967
• Knauer, Kolja (2009), "Chip-firing, antimatroids, and polyhedra",European Conference on Combinatorics, Graph Theory and Applications (EuroComb 2009),Electronic Notes in Discrete Mathematics, vol. 34, pp. 9–13,doi:10.1016/j.endm.2009.07.002,MR2591410
• Korte, Bernhard;Lovász, László;Schrader, Rainer (1991), "Chapter III: Abstract Convexity – Antimatroids",Greedoids,Springer-Verlag, pp. 19–43,doi:10.1007/978-3-642-58191-5_3,ISBN3-540-18190-3.
• Merchant, Nazarré; Riggle, Jason (2016),"OT grammars, beyond partial orders: ERC sets and antimatroids",Natural Language & Linguistic Theory,34:241–269,doi:10.1007/s11049-015-9297-5,S2CID170567540.
• Monjardet, Bernard (1985), "A use for frequently rediscovering a concept",Order,1(4): 415–417,doi:10.1007/BF00582748,S2CID119378521.
• Parmar, Aarati (2003), "Some Mathematical Structures Underlying Efficient Planning",AAAI Spring Symposium on Logical Formalization of Commonsense Reasoning(PDF).