Associative property

This article is about the associative property in mathematics. For associativity in the central processing unit memory cache, seeCPU cache § Associativity.For associativity in programming languages, seeoperator associativity.For the meaning of an associated group of people in linguistics, seeAssociativity (linguistics).

"Associative" and "non-associative" redirect here. For associative and non-associative learning, seeLearning § Types.

Inmathematics,theassociative propertyis a property of somebinary operationsthat means that rearranging theparenthesesin an expression will not change the result. Inpropositional logic,associativityis avalidrule of replacementforexpressionsinlogical proofs.

Associative property

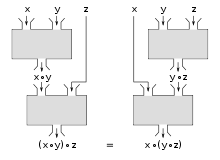A visual graph representing associative operations;$(x\circ y)\circ z=x\circ (y\circ z)$
Type	Law,rule of replacement
Field	Elementary algebra Boolean algebra Set theory Linear algebra Propositional calculus
Symbolic statement	Elementary algebra $(x\,*\,y)\,*\,z=x\,*\,(y\,*\,z)\forall x,y,z\in S$ Propositional calculus $(P\lor (Q\lor R))\Leftrightarrow ((P\lor Q)\lor R)$ $(P\land (Q\land R))\Leftrightarrow ((P\land Q)\land R),$

Within an expression containing two or more occurrences in a row of the same associative operator, the order in which theoperationsare performed does not matter as long as the sequence of theoperandsis not changed. That is (after rewriting the expression with parentheses and in infix notation if necessary), rearranging the parentheses in such an expression will not change its value. Consider the following equations:

$${\begin{aligned}(2+3)+4&=2+(3+4)=9\,\\2\times (3\times 4)&=(2\times 3)\times 4=24.\end{aligned}}$$

Even though the parentheses were rearranged on each line, the values of the expressions were not altered. Since this holds true when performing addition and multiplication on anyreal numbers,it can be said that "addition and multiplication of real numbers are associative operations".

Associativity is not the same ascommutativity,which addresses whether the order of two operands affects the result. For example, the order does not matter in the multiplication of real numbers, that is,a×b=b×a,so we say that the multiplication of real numbers is a commutative operation. However, operations such asfunction compositionandmatrix multiplicationare associative, but not (generally) commutative.

Associative operations are abundant in mathematics; in fact, manyalgebraic structures(such assemigroupsandcategories) explicitly require their binary operations to be associative.

However, many important and interesting operations are non-associative; some examples includesubtraction,exponentiation,and thevector cross product.In contrast to the theoretical properties of real numbers, the addition offloating pointnumbers in computer science is not associative, and the choice of how to associate an expression can have a significant effect on rounding error.

Definition

A binary operation ∗ on the setSis associative whenthis diagram commutes.That is, when the two paths fromS×S×StoScomposeto the same function fromS×S×StoS.

Formally, abinary operation$\ast$on asetSis calledassociativeif it satisfies theassociative law:

$(x\ast y)\ast z=x\ast (y\ast z)$,for all$x,y,z$inS.}}

Here, ∗ is used to replace the symbol of the operation, which may be any symbol, and even the absence of symbol (juxtaposition) as formultiplication.

$(xy)z=x(yz)$,for all$x,y,z$inS.

The associative law can also be expressed in functional notation thus:$(f\circ (g\circ h))(x)=((f\circ g)\circ h)(x)$

Generalized associative law

In the absence of the associative property, five factorsa,b,c,d,eresult in aTamari latticeof order four, possibly different products.

If a binary operation is associative, repeated application of the operation produces the same result regardless of how valid pairs of parentheses are inserted in the expression.This is called thegeneralized associative law.

The number of possible bracketings is just theCatalan number,$C_{n}$ , fornoperations onn+1values. For instance, a product of 3 operations on 4 elements may be written (ignoring permutations of the arguments), in$C_{3}=5$possible ways:

• $((ab)c)d$
• $(a(bc))d$
• $a((bc)d)$
• $(a(b(cd))$
• $(ab)(cd)$

If the product operation is associative, the generalized associative law says that all these expressions will yield the same result. So unless the expression with omitted parentheses already has a different meaning (see below), the parentheses can be considered unnecessary and "the" product can be written unambiguously as

$abcd$

As the number of elements increases, thenumber of possible ways to insert parenthesesgrows quickly, but they remain unnecessary for disambiguation.

An example where this does not work is thelogical biconditional↔.It is associative; thus,A↔ (B↔C)is equivalent to(A↔B) ↔C,butA↔B↔Cmost commonly means(A↔B) and (B↔C),which is not equivalent.

Examples

The addition of real numbers is associative.

Some examples of associative operations include the following.

• Theconcatenationof the three strings"hello","","world"can be computed by concatenating the first two strings (giving"hello") and appending the third string ("world"), or by joining the second and third string (giving"world") and concatenating the first string ("hello") with the result. The two methods produce the same result; string concatenation is associative (but not commutative).
• Inarithmetic,additionandmultiplicationofreal numbersare associative; i.e.,

  $$\left.{\begin{matrix}(x+y)+z=x+(y+z)=x+y+z\quad \\(x\,y)z=x(y\,z)=x\,y\,z\qquad \qquad \qquad \quad \ \ \,\end{matrix}}\right\}{\mbox{for all }}x,y,z\in \mathbb {R}.$$

  Because of associativity, the grouping parentheses can be omitted without ambiguity.
• The trivial operationx∗y=x(that is, the result is the first argument, no matter what the second argument is) is associative but not commutative. Likewise, the trivial operationx∘y=y(that is, the result is the second argument, no matter what the first argument is) is associative but not commutative.
• Addition and multiplication ofcomplex numbersandquaternionsare associative. Addition ofoctonionsis also associative, but multiplication of octonions is non-associative.
• Thegreatest common divisorandleast common multiplefunctions act associatively. $$\left.{\begin{matrix}\operatorname {gcd} (\operatorname {gcd} (x,y),z)=\operatorname {gcd} (x,\operatorname {gcd} (y,z))=\operatorname {gcd} (x,y,z)\ \quad \\\operatorname {lcm} (\operatorname {lcm} (x,y),z)=\operatorname {lcm} (x,\operatorname {lcm} (y,z))=\operatorname {lcm} (x,y,z)\quad \end{matrix}}\right\}{\mbox{ for all }}x,y,z\in \mathbb {Z}.$$
• Taking theintersectionor theunionofsets: $$\left.{\begin{matrix}(A\cap B)\cap C=A\cap (B\cap C)=A\cap B\cap C\quad \\(A\cup B)\cup C=A\cup (B\cup C)=A\cup B\cup C\quad \end{matrix}}\right\}{\mbox{for all sets }}A,B,C.$$
• IfMis some set andSdenotes the set of all functions fromMtoM,then the operation offunction compositiononSis associative:$$(f\circ g)\circ h=f\circ (g\circ h)=f\circ g\circ h\qquad {\mbox{for all }}f,g,h\in S.$$
• Slightly more generally, given four setsM,N,PandQ,withh:M→N,g:N→P,andf:P→Q,then $$(f\circ g)\circ h=f\circ (g\circ h)=f\circ g\circ h$$ as before. In short, composition of maps is always associative.
• Incategory theory,composition of morphisms is associative by definition. Associativity of functors and natural transformations follows from associativity of morphisms.
• Consider a set with three elements,A,B,andC.The following operation:

  ×	A	B	C
  A	A	A	A
  B	A	B	C
  C	A	A	A

  is associative. Thus, for example,A(BC) = (AB)C=A.This operation is not commutative.
• Becausematricesrepresentlinear functions,andmatrix multiplicationrepresents function composition, one can immediately conclude that matrix multiplication is associative.
• Forreal numbers(and for anytotally ordered set), the minimum and maximum operation is associative:$$\max(a,\max(b,c))=\max(\max(a,b),c)\quad {\text{ and }}\quad \min(a,\min(b,c))=\min(\min(a,b),c).$$

Propositional logic

Rule of replacement

In standard truth-functional propositional logic,association,orassociativityare twovalidrules of replacement.The rules allow one to move parentheses inlogical expressionsinlogical proofs.The rules (usinglogical connectivesnotation) are:

$$(P\lor (Q\lor R))\Leftrightarrow ((P\lor Q)\lor R)$$

and

$$(P\land (Q\land R))\Leftrightarrow ((P\land Q)\land R),$$

where "$\Leftrightarrow$"is ametalogicalsymbolrepresenting "can be replaced in aproofwith ".

Truth functional connectives

Associativityis a property of somelogical connectivesof truth-functionalpropositional logic.The followinglogical equivalencesdemonstrate that associativity is a property of particular connectives. The following (and their converses, since↔is commutative) are truth-functionaltautologies.

Associativity of disjunction

$((P\lor Q)\lor R)\leftrightarrow (P\lor (Q\lor R))$

Associativity of conjunction

$((P\land Q)\land R)\leftrightarrow (P\land (Q\land R))$

Associativity of equivalence

$((P\leftrightarrow Q)\leftrightarrow R)\leftrightarrow (P\leftrightarrow (Q\leftrightarrow R))$

Joint denialis an example of a truth functional connective that isnotassociative.

Non-associative operation

A binary operation$*$on a setSthat does not satisfy the associative law is callednon-associative.Symbolically,

$$(x*y)*z\neq x*(y*z)\qquad {\mbox{for some }}x,y,z\in S.$$

For such an operation the order of evaluationdoesmatter. For example:

Subtraction

$(5-3)-2\,\neq \,5-(3-2)$

Division

$(4/2)/2\,\neq \,4/(2/2)$

Exponentiation

$2^{(1^{2})}\,\neq \,(2^{1})^{2}$

Vector cross product

${\begin{aligned}\mathbf {i} \times (\mathbf {i} \times \mathbf {j} )&=\mathbf {i} \times \mathbf {k} =-\mathbf {j} \\(\mathbf {i} \times \mathbf {i} )\times \mathbf {j} &=\mathbf {0} \times \mathbf {j} =\mathbf {0} \end{aligned}}$

Also although addition is associative for finite sums, it is not associative inside infinite sums (series). For example, $$(1+-1)+(1+-1)+(1+-1)+(1+-1)+(1+-1)+(1+-1)+\dots =0$$ whereas $$1+(-1+1)+(-1+1)+(-1+1)+(-1+1)+(-1+1)+(-1+1)+\dots =1.$$

Some non-associative operations are fundamental in mathematics. They appear often as the multiplication in structures callednon-associative algebras,which have also an addition and ascalar multiplication.Examples are theoctonionsandLie algebras.In Lie algebras, the multiplication satisfiesJacobi identityinstead of the associative law; this allows abstracting the algebraic nature ofinfinitesimal transformations.

Other examples arequasigroup,quasifield,non-associative ring,andcommutative non-associative magmas.

Nonassociativity of floating point calculation

In mathematics, addition and multiplication of real numbers are associative. By contrast, in computer science, addition and multiplication offloating pointnumbers arenotassociative, as different rounding errors may be introduced when dissimilar-sized values are joined in a different order.

To illustrate this, consider a floating point representation with a 4-bitsignificand:

(1.000₂×2⁰+ 1.000₂×2⁰) + 1.000₂×2⁴= 1.000₂×2¹+ 1.000₂×2⁴= 1.001₂×2⁴

1.000₂×2⁰+ (1.000₂×2⁰+ 1.000₂×2⁴) = 1.000₂×2⁰+ 1.000₂×2⁴= 1.000₂×2⁴

Even though most computers compute with 24 or 53 bits of significand,this is still an important source of rounding error, and approaches such as theKahan summation algorithmare ways to minimise the errors. It can be especially problematic in parallel computing.

Notation for non-associative operations

Main article:Operator associativity

In general, parentheses must be used to indicate theorder of evaluationif a non-associative operation appears more than once in an expression (unless the notation specifies the order in another way, like${\dfrac {2}{3/4}}$). However,mathematiciansagree on a particular order of evaluation for several common non-associative operations. This is simply a notational convention to avoid parentheses.

Aleft-associativeoperation is a non-associative operation that is conventionally evaluated from left to right, i.e.,

$$\left.{\begin{array}{l}a*b*c=(a*b)*c\\a*b*c*d=((a*b)*c)*d\\a*b*c*d*e=(((a*b)*c)*d)*e\quad \\{\mbox{etc.}}\end{array}}\right\}{\mbox{for all }}a,b,c,d,e\in S$$

while aright-associativeoperation is conventionally evaluated from right to left:

$$\left.{\begin{array}{l}x*y*z=x*(y*z)\\w*x*y*z=w*(x*(y*z))\quad \\v*w*x*y*z=v*(w*(x*(y*z)))\quad \\{\mbox{etc.}}\end{array}}\right\}{\mbox{for all }}z,y,x,w,v\in S$$

Both left-associative and right-associative operations occur. Left-associative operations include the following:

Subtraction and division of real numbers

$x-y-z=(x-y)-z$

$x/y/z=(x/y)/z$

Function application

$(f\,x\,y)=((f\,x)\,y)$

This notation can be motivated by thecurryingisomorphism, which enables partial application.

Right-associative operations include the following:

Exponentiationof real numbers in superscript notation

$x^{y^{z}}=x^{(y^{z})}$

Exponentiation is commonly used with brackets or right-associatively because a repeated left-associative exponentiation operation is of little use. Repeated powers would mostly be rewritten with multiplication:

$(x^{y})^{z}=x^{(yz)}$

Formatted correctly, the superscript inherently behaves as a set of parentheses; e.g. in the expression$2^{x+3}$the addition is performedbeforethe exponentiation despite there being no explicit parentheses$2^{(x+3)}$wrapped around it. Thus given an expression such as$x^{y^{z}}$,the full exponent$y^{z}$of the base$x$is evaluated first. However, in some contexts, especially in handwriting, the difference between${x^{y}}^{z}=(x^{y})^{z}$,$x^{yz}=x^{(yz)}$and$x^{y^{z}}=x^{(y^{z})}$can be hard to see. In such a case, right-associativity is usually implied.

Function definition

$\mathbb {Z} \rightarrow \mathbb {Z} \rightarrow \mathbb {Z} =\mathbb {Z} \rightarrow (\mathbb {Z} \rightarrow \mathbb {Z} )$

$x\mapsto y\mapsto x-y=x\mapsto (y\mapsto x-y)$

Using right-associative notation for these operations can be motivated by theCurry–Howard correspondenceand by thecurryingisomorphism.

Non-associative operations for which no conventional evaluation order is defined include the following.

Exponentiation of real numbers in infix notation

$(x^{\wedge }y)^{\wedge }z\neq x^{\wedge }(y^{\wedge }z)$

Knuth's up-arrow operators

$a\uparrow \uparrow (b\uparrow \uparrow c)\neq (a\uparrow \uparrow b)\uparrow \uparrow c$

$a\uparrow \uparrow \uparrow (b\uparrow \uparrow \uparrow c)\neq (a\uparrow \uparrow \uparrow b)\uparrow \uparrow \uparrow c$

Taking thecross productof three vectors

${\vec {a}}\times ({\vec {b}}\times {\vec {c}})\neq ({\vec {a}}\times {\vec {b}})\times {\vec {c}}\qquad {\mbox{ for some }}{\vec {a}},{\vec {b}},{\vec {c}}\in \mathbb {R} ^{3}$

Taking the pairwiseaverageof real numbers

${(x+y)/2+z \over 2}\neq {x+(y+z)/2 \over 2}\qquad {\mbox{for all }}x,y,z\in \mathbb {R} {\mbox{ with }}x\neq z.$

Taking therelative complementof sets

$(A\backslash B)\backslash C\neq A\backslash (B\backslash C)$.

(Comparematerial nonimplicationin logic.)

History

William Rowan Hamiltonseems to have coined the term "associative property"around 1844, a time when he was contemplating the non-associative algebra of theoctonionshe had learned about fromJohn T. Graves.

See also

• Light's associativity test
• Telescoping series,the use of addition associativity for cancelling terms in an infiniteseries
• Asemigroupis a set with an associative binary operation.
• Commutativityanddistributivityare two other frequently discussed properties of binary operations.
• Power associativity,alternativity,flexibilityandN-ary associativityare weak forms of associativity.
• Moufang identitiesalso provide a weak form of associativity.