Banach space

Inmathematics,more specifically infunctional analysis,aBanach space(pronounced[ˈbanax]) is acompletenormed vector space.Thus, a Banach space is a vector space with ametricthat allows the computation ofvector lengthand distance between vectors and is complete in the sense that aCauchy sequenceof vectors always converges to a well-definedlimitthat is within the space.

Banach spaces are named after the Polish mathematicianStefan Banach,who introduced this concept and studied it systematically in 1920–1922 along withHans HahnandEduard Helly. Maurice René Fréchetwas the first to use the term "Banach space" and Banach in turn then coined the term "Fréchet space". Banach spaces originally grew out of the study offunction spacesbyHilbert,Fréchet,andRieszearlier in the century. Banach spaces play a central role in functional analysis. In other areas ofanalysis,the spaces under study are often Banach spaces.

Definition

ABanach spaceis acompletenormed space$\ (X,\|\cdot \|)~.$ A normed space is a pair $\ (X,\|\cdot \|)\$consisting of avector space$\ X\$over a scalar field$\mathbb {K}$(where$\ \mathbb {K} \$is commonly$\ \mathbb {R} \$or$\ \mathbb {C} \$) together with a distinguished norm$\ \|\cdot \|:X\to \mathbb {R} ~.$Like all norms, this norm induces atranslation invariant distance function,called thecanonicalor(norm)induced metric,defined for all vectors$\ x,y\in X\$by $$\ d(x,y):=\|y-x\|=\|x-y\|~.$$ This makes$X$into ametric space$\ (X,d)~.$ A sequence$\ x_{1},x_{2},\ldots \$is calledCauchy in$\ (X,d)\$or$d$-Cauchyor$\ \|\cdot \|$-Cauchyif for every real$\ r>0\,$there exists some index$N$such that $$\ d\left(x_{n},x_{m}\right)=\left\|x_{n}-x_{m}\right\|<r\$$ whenever$m$and$n$are greater than$\ N~.$ The normed space$\ (X,\|\cdot \|)\$is called aBanach spaceand the canonical metric$\ d\$is called acomplete metricif$\ (X,d)\$is acomplete metric space,which by definition means for everyCauchy sequence$\ x_{1},x_{2},\ldots \$in$\ (X,d)\,$there exists some$\ x\in X\$such that $$\lim _{n\to \infty }x_{n}=x\;{\text{ in }}(X,d)$$ where because$\left\|x_{n}-x\right\|=d\left(x_{n},x\right),$this sequence's convergence to$x$can equivalently be expressed as: $$\lim _{n\to \infty }\left\|x_{n}-x\right\|=0\;{\text{ in }}\mathbb {R} ~.$$

The norm$\ \|\cdot \|\$of a normed space$\ (X,\|\cdot \|)\$is called acomplete normif$\ (X,\|\cdot \|)\$is a Banach space.

L-semi-inner product

For any normed space$\ (X,\|\cdot \|)\,$there exists anL-semi-inner product$\ \langle \cdot,\cdot \rangle \$on$\ X\$such that${\textstyle \ \|x\|={\sqrt {\langle x,x\rangle }}\ }$for all$\ x\in X\;$in general, there may be infinitely many L-semi-inner products that satisfy this condition. L-semi-inner products are a generalization ofinner products,which are what fundamentally distinguishHilbert spacesfrom all other Banach spaces. This shows that all normed spaces (and hence all Banach spaces) can be considered as being generalizations of (pre-)Hilbert spaces.

Characterization in terms of series

The vector space structure allows one to relate the behavior of Cauchy sequences to that of convergingseries of vectors. A normed space$\ X\$is a Banach space if and only if eachabsolutely convergentseries in$\ X\$converges to a value that lies within$\ X\,$ $$\ \sum _{n=1}^{\infty }\|v_{n}\|<\infty \quad {\text{ implies that }}\quad \sum _{n=1}^{\infty }v_{n}\ \ {\text{ converges in }}\ \ X~.$$

Topology

The canonical metric$d$of a normed space$\ (X,\|\cdot \|)\$induces the usualmetric topology$\ \tau _{d}\$on$\ X\,$which is referred to as thecanonicalornorm inducedtopology. Every normed space is automatically assumed to carry thisHausdorfftopology, unless indicated otherwise. With this topology, every Banach space is aBaire space,although there exist normed spaces that are Baire but not Banach.The norm$\ \|\,\cdot \,\|:\left(X,\tau _{d}\right)\to \mathbb {R} \$is always acontinuous functionwith respect to the topology that it induces.

The open and closed balls of radius$r>0$centered at a point$\ x\in X\$are, respectively, the sets $$\ B_{r}(x):=\{\ z\in X:\|z-x\|<r\ \}\qquad {\text{ and }}\qquad C_{r}(x):=\{\ z\in X:\|z-x\|\leq r\ \}~.$$ Any such ball is aconvexandbounded subsetof$\ X\,$but acompactball /neighborhoodexists if and only if$\ X\$is afinite-dimensional vector space. In particular, no infinite–dimensional normed space can belocally compactor have theHeine–Borel property. If$\ x_{0}\$is a vector and$\ s\neq 0\$is a scalar then $$\ x_{0}+s\ B_{r}(x)=B_{|s|r}\!\left(\ x_{0}+s\ x\ \right)\qquad {\text{ and }}\qquad x_{0}+s\ C_{r}(x)=C_{|s|r}\!\left(\ x_{0}+s\ x\ \right)~.$$ Using$\ s=1\$shows that this norm-induced topology istranslation invariant,which means that for any$\ x\in X\$and$\ S\subseteq X\,$the subset$\ S\$isopen(respectively,closed) in$\ X\$if and only if this is true of its translation$\ x+S:=\{\ x+s:s\in S\ \}~.$ Consequently, the norm induced topology is completely determined by anyneighbourhood basisat the origin. Some common neighborhood bases at the origin include: $$\ \left\{\ B_{r}(0):r>0\ \right\},\qquad \left\{\ C_{r}(0):r>0\ \right\},\qquad \left\{\ B_{r_{n}}(0):n\in \mathbb {N} \ \right\},\qquad {\text{ or }}\qquad \left\{\ C_{r_{n}}(0):n\in \mathbb {N} \ \right\}\$$ where$\ r_{1},r_{2},\ldots \$is a sequence in of positive real numbers that converges to$\ 0\$in$\mathbb {R}$(such as$\ r_{n}:={\tfrac {1}{n}}\$or$\ r_{n}:=1/2^{n}\,$for instance). So for example, every open subset$\ U\$of$\ X\$can be written as a union $$\ U=\bigcup _{x\in I}B_{r_{x}}(x)=\bigcup _{x\in I}x+B_{r_{x}}(0)=\bigcup _{x\in I}x+r_{x}\ B_{1}(0)\$$ indexed by some subset$\ I\subseteq U\,$where every$\ r_{x}\$may be picked from the aforementioned sequence$\ r_{1},r_{2},\ldots \$(the open balls can be replaced with closed balls, although then the indexing set$\ I\$and radii$\ r_{x}\$may also need to be replaced). Additionally,$\ I\$can always be chosen to becountableif$\ X\$is aseparable space,which by definition means that$\ X\$contains some countabledense subset.

Homeomorphism classes of separable Banach spaces

All finite–dimensional normed spaces are separable Banach spaces and any two Banach spaces of the same finite dimension are linearly homeomorphic. Every separable infinite–dimensionalHilbert spaceis linearly isometrically isomorphic to the separable Hilbertsequence space$\ \ell ^{2}(\mathbb {N} )\$with itsusual norm$\ \|\cdot \|_{2}~.$

TheAnderson–Kadec theoremstates that every infinite–dimensional separableFréchet spaceishomeomorphicto theproduct space${\textstyle \ \prod _{i\in \mathbb {N} }\mathbb {R} \ }$of countably many copies of$\ \mathbb {R} \$(this homeomorphism need not be alinear map). Thus all infinite–dimensional separable Fréchet spaces are homeomorphic to each other (or said differently, their topology is uniqueup toa homeomorphism). Since every Banach space is a Fréchet space, this is also true of all infinite–dimensional separable Banach spaces, including$\ \ell ^{2}(\mathbb {N} )~.$ In fact,$\ \ell ^{2}(\mathbb {N} )\$is evenhomeomorphicto its ownunitsphere$\ \left\{\ x\in \ell ^{2}(\mathbb {N} ):\|x\|_{2}=1\ \right\}\,$which stands in sharp contrast to finite–dimensional spaces (theEuclidean plane$\ \mathbb {R} ^{2}\$is not homeomorphic to theunit circle,for instance).

This pattern inhomeomorphism classesextends to generalizations ofmetrizable(locally Euclidean)topological manifoldsknown asmetricBanach manifolds,which aremetric spacesthat are around every point,locally homeomorphicto some open subset of a given Banach space (metricHilbert manifoldsand metricFréchet manifoldsare defined similarly). For example, every open subset$\ U\$of a Banach space$X$is canonically a metric Banach manifold modeled on$\ X\$since theinclusion map$\ U\to X\$is anopenlocal homeomorphism. Using Hilbert spacemicrobundles,David Henderson showedin 1969 that every metric manifold modeled on a separable infinite–dimensional Banach (orFréchet) space can betopologically embeddedas anopensubsetof$\ \ell ^{2}(\mathbb {N} )\$and, consequently, also admits a uniquesmooth structuremaking it into a$\ C^{\infty }\$Hilbert manifold.

Compact and convex subsets

There is a compact subset$\ S\$of$\ \ell ^{2}(\mathbb {N} )\$whoseconvex hull$\ \operatorname {co} (S)\$isnotclosed and thus alsonotcompact (see this footnotefor an example). However, like in all Banach spaces, theclosedconvex hull$\ {\overline {\operatorname {co} }}S\$of this (and every other) compact subset will be compact.But if a normed space is not complete then it is in generalnotguaranteed that$\ {\overline {\operatorname {co} }}S\$will be compact whenever$S$is; an examplecan even be found in a (non-complete)pre-Hilbertvector subspace of$\ell ^{2}(\mathbb {N} ).$

As a topological vector space

This norm-induced topology also makes$\ \left(X,\tau _{d}\right)\$into what is known as atopological vector space(TVS), which by definition is a vector space endowed with a topology making the operations of addition and scalar multiplication continuous. It is emphasized that the TVS$\ \left(X,\tau _{d}\right)\$isonlya vector space together with a certain type of topology; that is to say, when considered as a TVS, it isnotassociated withanyparticular norm or metric (both of which are "forgotten"). This Hausdorff TVS$\left(X,\tau _{d}\right)$is evenlocally convexbecause the set of all open balls centered at the origin forms aneighbourhood basisat the origin consisting of convexbalancedopen sets. This TVS is alsonormable,which by definition refers to any TVS whose topology is induced by some (possibly unknown)norm.Normable TVSsare characterized bybeing Hausdorff and having aboundedconvexneighborhood of the origin. All Banach spaces arebarrelled spaces,which means that everybarrelis neighborhood of the origin (all closed balls centered at the origin are barrels, for example) and guarantees that theBanach–Steinhaus theoremholds.

Comparison of complete metrizable vector topologies

Theopen mapping theoremimplies that if$\tau$and$\ \tau _{2}\$are topologies on$\ X\$that make both$\ (X,\tau )\$and$\ (X,\tau _{2})\$intocomplete metrizable TVS(for example, Banach orFréchet spaces) and if one topology isfiner or coarserthan the other then they must be equal (that is, if$\tau \subseteq \tau _{2}$or$\ \tau _{2}\subseteq \tau \$then$\ \tau =\tau _{2}\$). So for example, if$\ (X,p)\$and$\ (X,q)\$are Banach spaces with topologies$\tau _{p}$and$\ \tau _{q}\$and if one of these spaces has some open ball that is also an open subset of the other space (or equivalently, if one of$\ p:\left(X,\tau _{q}\right)\to \mathbb {R} \$or$\ q:\left(X,\tau _{p}\right)\to \mathbb {R} \$is continuous) then their topologies are identical and theirnorms are equivalent.

Completeness

Complete norms and equivalent norms

Two norms,$\ p\$and$q,$on a vector space$\ X\$are said to beequivalentif they induce the same topology;this happens if and only if there exist positive real numbers$\ c,\ C>0\$such that${\textstyle \ c\ q(x)\leq p(x)\leq C\ q(x)\ }$for all$\ x\in X~.$If$\ p\$and$q$are two equivalent norms on a vector space$\ X\$then$\ (X,p)\$is a Banach space if and only if$\ (X,q)\$is a Banach space. See this footnote for an example of a continuous norm on a Banach space that isnotequivalent to that Banach space's given norm. All norms on a finite-dimensional vector space are equivalent and every finite-dimensional normed space is a Banach space.

Complete norms vs complete metrics

A metric$D$on a vector space$X$is induced by a norm on$X$if and only if$D$istranslation invariantandabsolutely homogeneous,which means that$D(sx,sy)=|s|D(x,y)$for all scalars$s$and all$x,y\in X,$in which case the function$\|x\|:=D(x,0)$defines a norm on$X$and the canonical metric induced by$\|\cdot \|$is equal to$D.$

Suppose that$(X,\|\cdot \|)$is a normed space and that$\tau$is the norm topology induced on$X.$Suppose that$D$isanymetricon$X$such that the topology that$D$induces on$X$is equal to$\tau.$If$D$istranslation invariantthen$(X,\|\cdot \|)$is a Banach space if and only if$(X,D)$is a complete metric space. If$D$isnottranslation invariant, then it may be possible for$(X,\|\cdot \|)$to be a Banach space but for$(X,D)$tonotbe a complete metric space(see this footnotefor an example). In contrast, a theorem of Klee,which also applies to allmetrizable topological vector spaces,implies that if there existsanycomplete metric$D$on$X$that induces the norm topology$\tau$on$X,$then$(X,\|\cdot \|)$is a Banach space.

AFréchet spaceis alocally convex topological vector spacewhose topology is induced by some translation-invariant complete metric. Every Banach space is a Fréchet space but not conversely; indeed, there even exist Fréchet spaces on which no norm is a continuous function (such as thespace of real sequences${\textstyle \ \mathbb {R} ^{\mathbb {N} }=\prod _{i\in \mathbb {N} }\mathbb {R} \ }$with theproduct topology). However, the topology of every Fréchet space is induced by somecountablefamily of real-valued (necessarily continuous) maps calledseminorms,which are generalizations ofnorms. It is even possible for a Fréchet space to have a topology that is induced by a countable family ofnorms(such norms would necessarily be continuous) but to not be a Banach/normable spacebecause its topology can not be defined by anysinglenorm. An example of such a space is theFréchet space$C^{\infty }(K),$whose definition can be found in the article onspaces of test functions and distributions.

Complete norms vs complete topological vector spaces

There is another notion of completeness besides metric completeness and that is the notion of acomplete topological vector space(TVS) or TVS-completeness, which uses the theory ofuniform spaces. Specifically, the notion of TVS-completeness uses a unique translation-invariantuniformity,called thecanonical uniformity,that dependsonlyon vector subtraction and the topology$\tau$that the vector space is endowed with, and so in particular, this notion of TVS completeness is independent of whatever norm induced the topology$\tau$(and even applies to TVSs that arenoteven metrizable). Every Banach space is a complete TVS. Moreover, a normed space is a Banach space (that is, its norm-induced metric is complete) if and only if it is complete as a topological vector space. If$(X,\tau )$is ametrizable topological vector space(such as any norm induced topology, for example), then$(X,\tau )$is a complete TVS if and only if it is asequentiallycomplete TVS, meaning that it is enough to check that every Cauchysequencein$(X,\tau )$converges in$(X,\tau )$to some point of$X$(that is, there is no need to consider the more general notion of arbitrary Cauchynets).

If$(X,\tau )$is a topological vector space whose topology is induced bysome(possibly unknown) norm (such spaces are callednormable), then$(X,\tau )$is a complete topological vector space if and only if$X$may be assigned anorm$\|\cdot \|$that induces on$X$the topology$\tau$and also makes$(X,\|\cdot \|)$into a Banach space. AHausdorfflocally convex topological vector space$X$isnormableif and only if itsstrong dual space$X_{b}^{\prime }$is normable,in which case$X_{b}^{\prime }$is a Banach space ($X_{b}^{\prime }$denotes thestrong dual spaceof$X,$whose topology is a generalization of thedual norm-induced topology on thecontinuous dual space$X^{\prime }$;see this footnotefor more details). If$X$is ametrizablelocally convex TVS, then$X$is normable if and only if$X_{b}^{\prime }$is aFréchet–Urysohn space. This shows that in the category oflocally convex TVSs,Banach spaces are exactly those complete spaces that are bothmetrizableand have metrizablestrong dual spaces.

Completions

Every normed space can beisometricallyembedded onto a dense vector subspace ofsomeBanach space, where this Banach space is called acompletionof the normed space. This Hausdorff completion is unique up toisometricisomorphism.

More precisely, for every normed space$X,$there exist a Banach space$Y$and a mapping$T:X\to Y$such that$T$is anisometric mappingand$T(X)$is dense in$Y.$If$Z$is another Banach space such that there is an isometric isomorphism from$X$onto a dense subset of$Z,$then$Z$is isometrically isomorphic to$Y.$ This Banach space$Y$is the Hausdorffcompletionof the normed space$X.$The underlying metric space for$Y$is the same as the metric completion of$X,$with the vector space operations extended from$X$to$Y.$The completion of$X$is sometimes denoted by${\widehat {X}}.$

General theory

Linear operators, isomorphisms

Main article:Bounded operator

If$X$and$Y$are normed spaces over the sameground field$\mathbb {K},$the set of allcontinuous$\mathbb {K}$-linear maps$T:X\to Y$is denoted by$B(X,Y).$In infinite-dimensional spaces, not all linear maps are continuous. A linear mapping from a normed space$X$to another normed space is continuous if and only if it isboundedon the closedunit ballof$X.$Thus, the vector space$B(X,Y)$can be given theoperator norm $$\|T\|=\sup \left\{\|Tx\|_{Y}\mid x\in X,\ \|x\|_{X}\leq 1\right\}.$$

For$Y$a Banach space, the space$B(X,Y)$is a Banach space with respect to this norm. In categorical contexts, it is sometimes convenient to restrict thefunction spacebetween two Banach spaces to only theshort maps;in that case the space$B(X,Y)$reappears as a naturalbifunctor.

If$X$is a Banach space, the space$B(X)=B(X,X)$forms a unitalBanach algebra;the multiplication operation is given by the composition of linear maps.

If$X$and$Y$are normed spaces, they areisomorphic normed spacesif there exists a linear bijection$T:X\to Y$such that$T$and its inverse$T^{-1}$are continuous. If one of the two spaces$X$or$Y$is complete (orreflexive,separable,etc.) then so is the other space. Two normed spaces$X$and$Y$areisometrically isomorphicif in addition,$T$is anisometry,that is,$\|T(x)\|=\|x\|$for every$x$in$X.$TheBanach–Mazur distance$d(X,Y)$between two isomorphic but not isometric spaces$X$and$Y$gives a measure of how much the two spaces$X$and$Y$differ.

Continuous and bounded linear functions and seminorms

Everycontinuous linear operatoris abounded linear operatorand if dealing only with normed spaces then the converse is also true. That is, alinear operatorbetween two normed spaces isboundedif and only if it is acontinuous function.So in particular, because the scalar field (which is$\mathbb {R}$or$\mathbb {C}$) is a normed space, alinear functionalon a normed space is abounded linear functionalif and only if it is acontinuous linear functional.This allows for continuity-related results (like those below) to be applied to Banach spaces. Although boundedness is the same as continuity for linear maps between normed spaces, the term "bounded" is more commonly used when dealing primarily with Banach spaces.

If$f:X\to \mathbb {R}$is asubadditive function(such as a norm, asublinear function,or real linear functional), then$f$iscontinuous at the originif and only if$f$isuniformly continuouson all of$X$;and if in addition$f(0)=0$then$f$is continuous if and only if itsabsolute value$|f|:X\to [0,\infty )$is continuous, which happens if and only if$\{x\in X:|f(x)|<1\}$is an open subset of$X.$ And very importantly for applying theHahn–Banach theorem,a linear functional$f$is continuous if and only if this is true of itsreal part$\operatorname {Re} f$and moreover,$\|\operatorname {Re} f\|=\|f\|$andthe real part$\operatorname {Re} f$completely determines$f,$which is why the Hahn–Banach theorem is often stated only for real linear functionals. Also, a linear functional$f$on$X$is continuous if and only if theseminorm$|f|$is continuous, which happens if and only if there exists a continuous seminorm$p:X\to \mathbb {R}$such that$|f|\leq p$;this last statement involving the linear functional$f$and seminorm$p$is encountered in many versions of the Hahn–Banach theorem.

Basic notions

The Cartesian product$X\times Y$of two normed spaces is not canonically equipped with a norm. However, several equivalent norms are commonly used,such as $$\|(x,y)\|_{1}=\|x\|+\|y\|,\qquad \|(x,y)\|_{\infty }=\max(\|x\|,\|y\|)$$ which correspond (respectively) to thecoproductandproductin the category of Banach spaces and short maps (discussed above).For finite (co)products, these norms give rise to isomorphic normed spaces, and the product$X\times Y$(or the direct sum$X\oplus Y$) is complete if and only if the two factors are complete.

If$M$is aclosedlinear subspaceof a normed space$X,$there is a natural norm on thequotient space$X/M,$ $$\|x+M\|=\inf \limits _{m\in M}\|x+m\|.$$

The quotient$X/M$is a Banach space when$X$is complete.Thequotient mapfrom$X$onto$X/M,$sending$x\in X$to its class$x+M,$is linear, onto and has norm$1,$except when$M=X,$in which case the quotient is the null space.

The closed linear subspace$M$of$X$is said to be acomplemented subspaceof$X$if$M$is therangeof asurjectivebounded linearprojection$P:X\to M.$In this case, the space$X$is isomorphic to the direct sum of$M$and$\ker P,$the kernel of the projection$P.$

Suppose that$X$and$Y$are Banach spaces and that$T\in B(X,Y).$There exists acanonical factorizationof$T$as $$T=T_{1}\circ \pi,\ \ \ T:X\ {\overset {\pi }{\longrightarrow }}\ X/\ker(T)\ {\overset {T_{1}}{\longrightarrow }}\ Y$$ where the first map$\pi$is the quotient map, and the second map$T_{1}$sends every class$x+\ker T$in the quotient to the image$T(x)$in$Y.$This is well defined because all elements in the same class have the same image. The mapping$T_{1}$is a linear bijection from$X/\ker T$onto the range$T(X),$whose inverse need not be bounded.

Classical spaces

Basic examplesof Banach spaces include: theLp spaces$L^{p}$and their special cases, thesequence spaces$\ell ^{p}$that consist of scalar sequences indexed bynatural numbers$\mathbb {N}$;among them, the space$\ell ^{1}$ofabsolutely summablesequences and the space$\ell ^{2}$of square summable sequences; the space$c_{0}$of sequences tending to zero and the space$\ell ^{\infty }$of bounded sequences; the space$C(K)$of continuous scalar functions on a compact Hausdorff space$K,$equipped with the max norm, $$\|f\|_{C(K)}=\max\{|f(x)|:x\in K\},\quad f\in C(K).$$

According to theBanach–Mazur theorem,every Banach space is isometrically isomorphic to a subspace of some$C(K).$For every separable Banach space$X,$there is a closed subspace$M$of$\ell ^{1}$such that$X:=\ell ^{1}/M.$

AnyHilbert spaceserves as an example of a Banach space. A Hilbert space$H$on$\mathbb {K} =\mathbb {R},\mathbb {C}$is complete for a norm of the form $$\|x\|_{H}={\sqrt {\langle x,x\rangle }},$$ where $$\langle \cdot,\cdot \rangle:H\times H\to \mathbb {K}$$ is theinner product,linear in its first argument that satisfies the following: $${\begin{aligned}\langle y,x\rangle &={\overline {\langle x,y\rangle }},\quad {\text{ for all }}x,y\in H\\\langle x,x\rangle &\geq 0,\quad {\text{ for all }}x\in H\\\langle x,x\rangle =0{\text{ if and only if }}x&=0.\end{aligned}}$$

For example, the space$L^{2}$is a Hilbert space.

TheHardy spaces,theSobolev spacesare examples of Banach spaces that are related to$L^{p}$spaces and have additional structure. They are important in different branches of analysis,Harmonic analysisandPartial differential equationsamong others.

Banach algebras

ABanach algebrais a Banach space$A$over$\mathbb {K} =\mathbb {R}$or$\mathbb {C},$together with a structure ofalgebra over$\mathbb {K}$,such that the product map$A\times A\ni (a,b)\mapsto ab\in A$is continuous. An equivalent norm on$A$can be found so that$\|ab\|\leq \|a\|\|b\|$for all$a,b\in A.$

Examples

• The Banach space$C(K)$with the pointwise product, is a Banach algebra.
• Thedisk algebra$A(\mathbf {D} )$consists of functionsholomorphicin the open unit disk$D\subseteq \mathbb {C}$and continuous on itsclosure:${\overline {\mathbf {D} }}.$Equipped with the max norm on${\overline {\mathbf {D} }},$the disk algebra$A(\mathbf {D} )$is a closed subalgebra of$C\left({\overline {\mathbf {D} }}\right).$
• TheWiener algebra$A(\mathbf {T} )$is the algebra of functions on the unit circle$\mathbf {T}$with absolutely convergent Fourier series. Via the map associating a function on$\mathbf {T}$to the sequence of its Fourier coefficients, this algebra is isomorphic to the Banach algebra$\ell ^{1}(Z),$where the product is theconvolutionof sequences.
• For every Banach space$X,$the space$B(X)$of bounded linear operators on$X,$with the composition of maps as product, is a Banach algebra.
• AC*-algebrais a complex Banach algebra$A$with anantilinearinvolution$a\mapsto a^{*}$such that$\left\|a^{*}a\right\|=\|a\|^{2}.$The space$B(H)$of bounded linear operators on a Hilbert space$H$is a fundamental example of C*-algebra. TheGelfand–Naimark theoremstates that every C*-algebra is isometrically isomorphic to a C*-subalgebra of some$B(H).$The space$C(K)$of complex continuous functions on a compact Hausdorff space$K$is an example of commutative C*-algebra, where the involution associates to every function$f$itscomplex conjugate${\overline {f}}.$

Dual space

Main article:Dual space

If$X$is a normed space and$\mathbb {K}$the underlyingfield(either therealor thecomplex numbers), thecontinuous dual spaceis the space of continuous linear maps from$X$into$\mathbb {K},$orcontinuous linear functionals. The notation for the continuous dual is$X^{\prime }=B(X,\mathbb {K} )$in this article. Since$\mathbb {K}$is a Banach space (using theabsolute valueas norm), the dual$X^{\prime }$is a Banach space, for every normed space$X.$TheDixmier–Ng theoremcharacterizes the dual spaces of Banach spaces.

The main tool for proving the existence of continuous linear functionals is theHahn–Banach theorem.

Hahn–Banach theorem—Let$X$be avector spaceover the field$\mathbb {K} =\mathbb {R},\mathbb {C}.$Let further

• $Y\subseteq X$be alinear subspace,
• $p:X\to \mathbb {R}$be asublinear functionand
• $f:Y\to \mathbb {K}$be alinear functionalso that$\operatorname {Re} (f(y))\leq p(y)$for all$y\in Y.$

Then, there exists a linear functional$F:X\to \mathbb {K}$so that$$F{\big \vert }_{Y}=f,\quad {\text{ and }}\quad {\text{ for all }}x\in X,\ \ \operatorname {Re} (F(x))\leq p(x).$$

In particular, every continuous linear functional on a subspace of a normed space can be continuously extended to the whole space, without increasing the norm of the functional. An important special case is the following: for every vector$x$in a normed space$X,$there exists a continuous linear functional$f$on$X$such that $$f(x)=\|x\|_{X},\quad \|f\|_{X^{\prime }}\leq 1.$$

When$x$is not equal to the$\mathbf {0}$vector, the functional$f$must have norm one, and is called anorming functionalfor$x.$

TheHahn–Banach separation theoremstates that two disjoint non-emptyconvex setsin a real Banach space, one of them open, can be separated by a closedaffinehyperplane. The open convex set lies strictly on one side of the hyperplane, the second convex set lies on the other side but may touch the hyperplane.

A subset$S$in a Banach space$X$istotalif thelinear spanof$S$isdensein$X.$The subset$S$is total in$X$if and only if the only continuous linear functional that vanishes on$S$is the$\mathbf {0}$functional: this equivalence follows from the Hahn–Banach theorem.

If$X$is the direct sum of two closed linear subspaces$M$and$N,$then the dual$X^{\prime }$of$X$is isomorphic to the direct sum of the duals of$M$and$N.$ If$M$is a closed linear subspace in$X,$one can associate theorthogonal of$M$in the dual, $$M^{\bot }=\left\{x^{\prime }\in X:x^{\prime }(m)=0,\ {\text{ for all }}m\in M\right\}.$$

The orthogonal$M^{\bot }$is a closed linear subspace of the dual. The dual of$M$is isometrically isomorphic to$X'/M^{\bot }.$ The dual of$X/M$is isometrically isomorphic to$M^{\bot }.$

The dual of a separable Banach space need not be separable, but:

Theorem—Let$X$be a normed space. If$X'$isseparable,then$X$is separable.

When$X'$is separable, the above criterion for totality can be used for proving the existence of a countable total subset in$X.$

Weak topologies

Theweak topologyon a Banach space$X$is thecoarsest topologyon$X$for which all elements$x^{\prime }$in the continuous dual space$X^{\prime }$are continuous. The norm topology is thereforefinerthan the weak topology. It follows from the Hahn–Banach separation theorem that the weak topology isHausdorff,and that a norm-closedconvex subsetof a Banach space is also weakly closed. A norm-continuous linear map between two Banach spaces$X$and$Y$is alsoweakly continuous,that is, continuous from the weak topology of$X$to that of$Y.$

If$X$is infinite-dimensional, there exist linear maps which are not continuous. The space$X^{*}$of all linear maps from$X$to the underlying field$\mathbb {K}$(this space$X^{*}$is called thealgebraic dual space,to distinguish it from$X^{\prime }$also induces a topology on$X$which isfinerthan the weak topology, and much less used in functional analysis.

On a dual space$X^{\prime },$there is a topology weaker than the weak topology of$X^{\prime },$calledweak* topology. It is the coarsest topology on$X^{\prime }$for which all evaluation maps$x^{\prime }\in X^{\prime }\mapsto x^{\prime }(x),$where$x$ranges over$X,$are continuous. Its importance comes from theBanach–Alaoglu theorem.

Banach–Alaoglu theorem—Let$X$be anormed vector space.Then theclosedunit ball$B=\left\{x\in X:\|x\|\leq 1\right\}$of the dual space iscompactin the weak* topology.

The Banach–Alaoglu theorem can be proved usingTychonoff's theoremabout infinite products of compact Hausdorff spaces. When$X$is separable, the unit ball$B^{\prime }$of the dual is ametrizablecompact in the weak* topology.

Examples of dual spaces

The dual of$c_{0}$is isometrically isomorphic to$\ell ^{1}$:for every bounded linear functional$f$on$c_{0},$there is a unique element$y=\left\{y_{n}\right\}\in \ell ^{1}$such that $$f(x)=\sum _{n\in \mathbb {N} }x_{n}y_{n},\qquad x=\{x_{n}\}\in c_{0},\ \ {\text{and}}\ \ \|f\|_{(c_{0})'}=\|y\|_{\ell _{1}}.$$

The dual of$\ell ^{1}$is isometrically isomorphic to$\ell ^{\infty }$. The dual ofLebesgue space$L^{p}([0,1])$is isometrically isomorphic to$L^{q}([0,1])$when$1\leq p<\infty$and${\frac {1}{p}}+{\frac {1}{q}}=1.$

For every vector$y$in a Hilbert space$H,$the mapping $$x\in H\to f_{y}(x)=\langle x,y\rangle$$

defines a continuous linear functional$f_{y}$on$H.$TheRiesz representation theoremstates that every continuous linear functional on$H$is of the form$f_{y}$for a uniquely defined vector$y$in$H.$ The mapping$y\in H\to f_{y}$is anantilinearisometric bijection from$H$onto its dual$H'.$ When the scalars are real, this map is an isometric isomorphism.

When$K$is a compact Hausdorff topological space, the dual$M(K)$of$C(K)$is the space ofRadon measuresin the sense of Bourbaki. The subset$P(K)$of$M(K)$consisting of non-negative measures of mass 1 (probability measures) is a convex w*-closed subset of the unit ball of$M(K).$ Theextreme pointsof$P(K)$are theDirac measureson$K.$ The set of Dirac measures on$K,$equipped with the w*-topology, ishomeomorphicto$K.$

Banach–Stone Theorem—If$K$and$L$are compact Hausdorff spaces and if$C(K)$and$C(L)$are isometrically isomorphic, then the topological spaces$K$and$L$arehomeomorphic.

The result has been extended by Amirand Cambernto the case when the multiplicativeBanach–Mazur distancebetween$C(K)$and$C(L)$is$<2.$ The theorem is no longer true when the distance is$=2.$

In the commutativeBanach algebra$C(K),$themaximal idealsare precisely kernels of Dirac measures on$K,$ $$I_{x}=\ker \delta _{x}=\{f\in C(K):f(x)=0\},\quad x\in K.$$

More generally, by theGelfand–Mazur theorem,the maximal ideals of a unital commutative Banach algebra can be identified with itscharacters—not merely as sets but as topological spaces: the former with thehull-kernel topologyand the latter with the w*-topology. In this identification, the maximal ideal space can be viewed as a w*-compact subset of the unit ball in the dual$A'.$

Theorem—If$K$is a compact Hausdorff space, then the maximal ideal space$\Xi$of the Banach algebra$C(K)$ishomeomorphicto$K.$

Not every unital commutative Banach algebra is of the form$C(K)$for some compact Hausdorff space$K.$However, this statement holds if one places$C(K)$in the smaller category of commutativeC*-algebras. Gelfand'srepresentation theoremfor commutative C*-algebras states that every commutative unitalC*-algebra$A$is isometrically isomorphic to a$C(K)$space. The Hausdorff compact space$K$here is again the maximal ideal space, also called thespectrumof$A$in the C*-algebra context.

Bidual

See also:Bidual,Reflexive space,andSemi-reflexive space

If$X$is a normed space, the (continuous) dual$X''$of the dual$X'$is calledbidual,orsecond dualof$X.$ For every normed space$X,$there is a natural map, $${\begin{cases}F_{X}\colon X\to X''\\F_{X}(x)(f)=f(x)&{\text{ for all }}x\in X,{\text{ and for all }}f\in X'\end{cases}}$$

This defines$F_{X}(x)$as a continuous linear functional on$X^{\prime },$that is, an element of$X^{\prime \prime }.$The map$F_{X}\colon x\to F_{X}(x)$is a linear map from$X$to$X^{\prime \prime }.$ As a consequence of the existence of anorming functional$f$for every$x\in X,$this map$F_{X}$is isometric, thusinjective.

For example, the dual of$X=c_{0}$is identified with$\ell ^{1},$and the dual of$\ell ^{1}$is identified with$\ell ^{\infty },$the space of bounded scalar sequences. Under these identifications,$F_{X}$is the inclusion map from$c_{0}$to$\ell ^{\infty }.$It is indeed isometric, but not onto.

If$F_{X}$issurjective,then the normed space$X$is calledreflexive(seebelow). Being the dual of a normed space, the bidual$X''$is complete, therefore, every reflexive normed space is a Banach space.

Using the isometric embedding$F_{X},$it is customary to consider a normed space$X$as a subset of its bidual. When$X$is a Banach space, it is viewed as a closed linear subspace of$X^{\prime \prime }.$If$X$is not reflexive, the unit ball of$X$is a proper subset of the unit ball of$X^{\prime \prime }.$ TheGoldstine theoremstates that the unit ball of a normed space is weakly*-dense in the unit ball of the bidual. In other words, for every$x''$in the bidual, there exists anet$\left(x_{i}\right)_{i\in I}$in$X$so that $$\sup _{i\in I}\left\|x_{i}\right\|\leq \|x''\|,\ \ x''(f)=\lim _{i}f\left(x_{i}\right),\quad f\in X'.$$

The net may be replaced by a weakly*-convergent sequence when the dual$X'$is separable. On the other hand, elements of the bidual of$\ell ^{1}$that are not in$\ell ^{1}$cannot be weak*-limit ofsequencesin$\ell ^{1},$since$\ell ^{1}$isweakly sequentially complete.

Banach's theorems

Here are the main general results about Banach spaces that go back to the time of Banach's book (Banach (1932)) and are related to theBaire category theorem. According to this theorem, a complete metric space (such as a Banach space, aFréchet spaceor anF-space) cannot be equal to a union of countably many closed subsets with emptyinteriors. Therefore, a Banach space cannot be the union of countably many closed subspaces, unless it is already equal to one of them; a Banach space with a countableHamel basisis finite-dimensional.

Banach–Steinhaus Theorem—Let$X$be a Banach space and$Y$be anormed vector space.Suppose that$F$is a collection of continuous linear operators from$X$to$Y.$The uniform boundedness principle states that if for all$x$in$X$we have$\sup _{T\in F}\|T(x)\|_{Y}<\infty,$then$\sup _{T\in F}\|T\|_{Y}<\infty.$

The Banach–Steinhaus theorem is not limited to Banach spaces. It can be extended for example to the case where$X$is aFréchet space,provided the conclusion is modified as follows: under the same hypothesis, there exists a neighborhood$U$of$\mathbf {0}$in$X$such that all$T$in$F$are uniformly bounded on$U,$ $$\sup _{T\in F}\sup _{x\in U}\;\|T(x)\|_{Y}<\infty.$$

The Open Mapping Theorem—Let$X$and$Y$be Banach spaces and$T:X\to Y$be a surjective continuous linear operator, then$T$is an open map.

Corollary—Every one-to-one bounded linear operator from a Banach space onto a Banach space is an isomorphism.

The First Isomorphism Theorem for Banach spaces—Suppose that$X$and$Y$are Banach spaces and that$T\in B(X,Y).$Suppose further that the range of$T$is closed in$Y.$Then$X/\ker T$is isomorphic to$T(X).$

This result is a direct consequence of the precedingBanach isomorphism theoremand of the canonical factorization of bounded linear maps.

Corollary—If a Banach space$X$is the internal direct sum of closed subspaces$M_{1},\ldots,M_{n},$then$X$is isomorphic to$M_{1}\oplus \cdots \oplus M_{n}.$

This is another consequence of Banach's isomorphism theorem, applied to the continuous bijection from$M_{1}\oplus \cdots \oplus M_{n}$onto$X$sending$m_{1},\cdots,m_{n}$to the sum$m_{1}+\cdots +m_{n}.$

The Closed Graph Theorem—Let$T:X\to Y$be a linear mapping between Banach spaces. The graph of$T$is closed in$X\times Y$if and only if$T$is continuous.

Reflexivity

Main article:Reflexive space

The normed space$X$is calledreflexivewhen the natural map $${\begin{cases}F_{X}:X\to X''\\F_{X}(x)(f)=f(x)&{\text{ for all }}x\in X,{\text{ and for all }}f\in X'\end{cases}}$$ is surjective. Reflexive normed spaces are Banach spaces.

Theorem—If$X$is a reflexive Banach space, every closed subspace of$X$and every quotient space of$X$are reflexive.

This is a consequence of the Hahn–Banach theorem. Further, by the open mapping theorem, if there is a bounded linear operator from the Banach space$X$onto the Banach space$Y,$then$Y$is reflexive.

Theorem—If$X$is a Banach space, then$X$is reflexive if and only if$X^{\prime }$is reflexive.

Corollary—Let$X$be a reflexive Banach space. Then$X$isseparableif and only if$X^{\prime }$is separable.

Indeed, if the dual$Y^{\prime }$of a Banach space$Y$is separable, then$Y$is separable. If$X$is reflexive and separable, then the dual of$X^{\prime }$is separable, so$X^{\prime }$is separable.

Theorem—Suppose that$X_{1},\ldots,X_{n}$are normed spaces and that$X=X_{1}\oplus \cdots \oplus X_{n}.$Then$X$is reflexive if and only if each$X_{j}$is reflexive.

Hilbert spaces are reflexive. The$L^{p}$spaces are reflexive when$1<p<\infty.$More generally,uniformly convex spacesare reflexive, by theMilman–Pettis theorem. The spaces$c_{0},\ell ^{1},L^{1}([0,1]),C([0,1])$are not reflexive. In these examples of non-reflexive spaces$X,$the bidual$X''$is "much larger" than$X.$ Namely, under the natural isometric embedding of$X$into$X''$given by the Hahn–Banach theorem, the quotient$X^{\prime \prime }/X$is infinite-dimensional, and even nonseparable. However, Robert C. James has constructed an exampleof a non-reflexive space, usually called "the James space"and denoted by$J,$such that the quotient$J^{\prime \prime }/J$is one-dimensional. Furthermore, this space$J$is isometrically isomorphic to its bidual.

Theorem—A Banach space$X$is reflexive if and only if its unit ball iscompactin theweak topology.

When$X$is reflexive, it follows that all closed and boundedconvex subsetsof$X$are weakly compact. In a Hilbert space$H,$the weak compactness of the unit ball is very often used in the following way: every bounded sequence in$H$has weakly convergent subsequences.

Weak compactness of the unit ball provides a tool for finding solutions in reflexive spaces to certainoptimization problems. For example, everyconvexcontinuous function on the unit ball$B$of a reflexive space attains its minimum at some point in$B.$

As a special case of the preceding result, when$X$is a reflexive space over$\mathbb {R},$every continuous linear functional$f$in$X^{\prime }$attains its maximum$\|f\|$on the unit ball of$X.$ The followingtheorem of Robert C. Jamesprovides a converse statement.

James' Theorem—For a Banach space the following two properties are equivalent:

• $X$is reflexive.
• for all$f$in$X^{\prime }$there exists$x\in X$with$\|x\|\leq 1,$so that$f(x)=\|f\|.$

The theorem can be extended to give a characterization of weakly compact convex sets.

On every non-reflexive Banach space$X,$there exist continuous linear functionals that are notnorm-attaining. However, theBishop–Phelpstheoremstates that norm-attaining functionals are norm dense in the dual$X^{\prime }$of$X.$

Weak convergences of sequences

A sequence$\left\{x_{n}\right\}$in a Banach space$X$isweakly convergentto a vector$x\in X$if$\left\{f\left(x_{n}\right)\right\}$converges to$f(x)$for every continuous linear functional$f$in the dual$X^{\prime }.$The sequence$\left\{x_{n}\right\}$is aweakly Cauchy sequenceif$\left\{f\left(x_{n}\right)\right\}$converges to a scalar limit$L(f),,$for every$f$in$X^{\prime }.$ A sequence$\left\{f_{n}\right\}$in the dual$X^{\prime }$isweakly* convergentto a functional$f\in X^{\prime }$if$f_{n}(x)$converges to$f(x)$for every$x$in$X.$ Weakly Cauchy sequences, weakly convergent and weakly* convergent sequences are norm bounded, as a consequence of theBanach–Steinhaustheorem.

When the sequence$\left\{x_{n}\right\}$in$X$is a weakly Cauchy sequence, the limit$L$above defines a bounded linear functional on the dual$X^{\prime },$that is, an element$L$of the bidual of$X,$and$L$is the limit of$\left\{x_{n}\right\}$in the weak*-topology of the bidual. The Banach space$X$isweakly sequentially completeif every weakly Cauchy sequence is weakly convergent in$X.$ It follows from the preceding discussion that reflexive spaces are weakly sequentially complete.

Theorem—For every measure$\mu,$the space$L^{1}(\mu )$is weakly sequentially complete.

An orthonormal sequence in a Hilbert space is a simple example of a weakly convergent sequence, with limit equal to the$\mathbf {0}$vector. Theunit vector basisof$\ell ^{p}$for$1<p<\infty,$or of$c_{0},$is another example of aweakly null sequence,that is, a sequence that converges weakly to$\mathbf {0}.$ For every weakly null sequence in a Banach space, there exists a sequence of convex combinations of vectors from the given sequence that is norm-converging to$\mathbf {0}.$

The unit vector basis of$\ell ^{1}$is not weakly Cauchy. Weakly Cauchy sequences in$\ell ^{1}$are weakly convergent, since$L^{1}$-spaces are weakly sequentially complete. Actually, weakly convergent sequences in$\ell ^{1}$are norm convergent.This means that$\ell ^{1}$satisfiesSchur's property.

Results involving the$\ell ^{1}$basis

Weakly Cauchy sequences and the$\ell ^{1}$basis are the opposite cases of the dichotomy established in the following deep result of H. P. Rosenthal.

Theorem—Let$\left\{x_{n}\right\}_{n\in \mathbb {N} }$be a bounded sequence in a Banach space. Either$\left\{x_{n}\right\}_{n\in \mathbb {N} }$has a weakly Cauchy subsequence, or it admits a subsequenceequivalentto the standard unit vector basis of$\ell ^{1}.$

A complement to this result is due to Odell and Rosenthal (1975).

Theorem—Let$X$be a separable Banach space. The following are equivalent:

• The space$X$does not contain a closed subspace isomorphic to$\ell ^{1}.$
• Every element of the bidual$X''$is the weak*-limit of a sequence$\left\{x_{n}\right\}$in$X.$

By the Goldstine theorem, every element of the unit ball$B^{\prime \prime }$of$X^{\prime \prime }$is weak*-limit of a net in the unit ball of$X.$When$X$does not contain$\ell ^{1},$every element of$B^{\prime \prime }$is weak*-limit of asequencein the unit ball of$X.$

When the Banach space$X$is separable, the unit ball of the dual$X^{\prime },$equipped with the weak*-topology, is a metrizable compact space$K,$and every element$x^{\prime \prime }$in the bidual$X^{\prime \prime }$defines a bounded function on$K$: $$x'\in K\mapsto x''(x'),\quad \left|x''(x')\right|\leq \left\|x''\right\|.$$

This function is continuous for the compact topology of$K$if and only if$x^{\prime \prime }$is actually in$X,$considered as subset of$X^{\prime \prime }.$ Assume in addition for the rest of the paragraph that$X$does not contain$\ell ^{1}.$ By the preceding result of Odell and Rosenthal, the function$x^{\prime \prime }$is thepointwise limiton$K$of a sequence$\left\{x_{n}\right\}\subseteq X$of continuous functions on$K,$it is therefore afirst Baire class functionon$K.$ The unit ball of the bidual is a pointwise compact subset of the first Baire class on$K.$

Sequences, weak and weak* compactness

When$X$is separable, the unit ball of the dual is weak*-compact by theBanach–Alaoglu theoremand metrizable for the weak* topology,hence every bounded sequence in the dual has weakly* convergent subsequences. This applies to separable reflexive spaces, but more is true in this case, as stated below.

The weak topology of a Banach space$X$is metrizable if and only if$X$is finite-dimensional.If the dual$X'$is separable, the weak topology of the unit ball of$X$is metrizable. This applies in particular to separable reflexive Banach spaces. Although the weak topology of the unit ball is not metrizable in general, one can characterize weak compactness using sequences.

Eberlein–Šmulian theorem—A set$A$in a Banach space is relatively weakly compact if and only if every sequence$\left\{a_{n}\right\}$in$A$has a weakly convergent subsequence.

A Banach space$X$is reflexive if and only if each bounded sequence in$X$has a weakly convergent subsequence.

A weakly compact subset$A$in$\ell ^{1}$is norm-compact. Indeed, every sequence in$A$has weakly convergent subsequences by Eberlein–Šmulian, that are norm convergent by the Schur property of$\ell ^{1}.$

Type and cotype

Main article:Type and cotype of a Banach space

A way to classify Banach spaces is through the probabilistic notion oftype and cotype,these two measure how far a Banach space is from a Hilbert space.

Schauder bases

Main article:Schauder basis

ASchauder basisin a Banach space$X$is a sequence$\left\{e_{n}\right\}_{n\geq 0}$of vectors in$X$with the property that for every vector$x\in X,$there existuniquelydefined scalars$\left\{x_{n}\right\}_{n\geq 0}$depending on$x,$such that $$x=\sum _{n=0}^{\infty }x_{n}e_{n},\quad {\textit {i.e.,}}\quad x=\lim _{n}P_{n}(x),\ P_{n}(x):=\sum _{k=0}^{n}x_{k}e_{k}.$$

Banach spaces with a Schauder basis are necessarilyseparable,because the countable set of finite linear combinations with rational coefficients (say) is dense.

It follows from the Banach–Steinhaus theorem that the linear mappings$\left\{P_{n}\right\}$are uniformly bounded by some constant$C.$ Let$\left\{e_{n}^{*}\right\}$denote the coordinate functionals which assign to every$x$in$X$the coordinate$x_{n}$of$x$in the above expansion. They are calledbiorthogonal functionals.When the basis vectors have norm$1,$the coordinate functionals$\left\{e_{n}^{*}\right\}$have norm$\,\leq 2C$in the dual of$X.$

Most classical separable spaces have explicit bases. TheHaar system$\left\{h_{n}\right\}$is a basis for$L^{p}([0,1]),1\leq p<\infty.$ Thetrigonometric systemis a basis in$L^{p}(\mathbf {T} )$when$1<p<\infty.$ TheSchauder systemis a basis in the space$C([0,1]).$ The question of whether the disk algebra$A(\mathbf {D} )$has a basisremained open for more than forty years, until Bočkarev showed in 1974 that$A(\mathbf {D} )$admits a basis constructed from theFranklin system.

Since every vector$x$in a Banach space$X$with a basis is the limit of$P_{n}(x),$with$P_{n}$of finite rank and uniformly bounded, the space$X$satisfies thebounded approximation property. The first example byEnfloof a space failing the approximation property was at the same time the first example of a separable Banach space without a Schauder basis.

Robert C. James characterized reflexivity in Banach spaces with a basis: the space$X$with a Schauder basis is reflexive if and only if the basis is bothshrinking and boundedly complete. In this case, the biorthogonal functionals form a basis of the dual of$X.$

Tensor product

Main articles:Tensor productandTopological tensor product

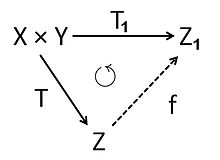
Let$X$and$Y$be two$\mathbb {K}$-vector spaces. Thetensor product$X\otimes Y$of$X$and$Y$is a$\mathbb {K}$-vector space$Z$with a bilinear mapping$T:X\times Y\to Z$which has the followinguniversal property:

If$T_{1}:X\times Y\to Z_{1}$is any bilinear mapping into a$\mathbb {K}$-vector space$Z_{1},$then there exists a unique linear mapping$f:Z\to Z_{1}$such that$T_{1}=f\circ T.$

The image under$T$of a couple$(x,y)$in$X\times Y$is denoted by$x\otimes y,$and called asimple tensor. Every element$z$in$X\otimes Y$is a finite sum of such simple tensors.

There are various norms that can be placed on the tensor product of the underlying vector spaces, amongst others theprojective cross normandinjective cross normintroduced byA. Grothendieckin 1955.

In general, the tensor product of complete spaces is not complete again. When working with Banach spaces, it is customary to say that theprojective tensor productof two Banach spaces$X$and$Y$is thecompletion$X{\widehat {\otimes }}_{\pi }Y$of the algebraic tensor product$X\otimes Y$equipped with the projective tensor norm, and similarly for theinjective tensor product$X{\widehat {\otimes }}_{\varepsilon }Y.$ Grothendieck proved in particular that

$${\begin{aligned}C(K){\widehat {\otimes }}_{\varepsilon }Y&\simeq C(K,Y),\\L^{1}([0,1]){\widehat {\otimes }}_{\pi }Y&\simeq L^{1}([0,1],Y),\end{aligned}}$$ where$K$is a compact Hausdorff space,$C(K,Y)$the Banach space of continuous functions from$K$to$Y$and$L^{1}([0,1],Y)$the space of Bochner-measurable and integrable functions from$[0,1]$to$Y,$and where the isomorphisms are isometric. The two isomorphisms above are the respective extensions of the map sending the tensor$f\otimes y$to the vector-valued function$s\in K\to f(s)y\in Y.$

Tensor products and the approximation property

Let$X$be a Banach space. The tensor product$X'{\widehat {\otimes }}_{\varepsilon }X$is identified isometrically with the closure in$B(X)$of the set of finite rank operators. When$X$has theapproximation property,this closure coincides with the space ofcompact operatorson$X.$

For every Banach space$Y,$there is a natural norm$1$linear map $$Y{\widehat {\otimes }}_{\pi }X\to Y{\widehat {\otimes }}_{\varepsilon }X$$ obtained by extending the identity map of the algebraic tensor product. Grothendieck related theapproximation problemto the question of whether this map is one-to-one when$Y$is the dual of$X.$ Precisely, for every Banach space$X,$the map $$X'{\widehat {\otimes }}_{\pi }X\ \longrightarrow X'{\widehat {\otimes }}_{\varepsilon }X$$ is one-to-one if and only if$X$has the approximation property.

Grothendieck conjectured that$X{\widehat {\otimes }}_{\pi }Y$and$X{\widehat {\otimes }}_{\varepsilon }Y$must be different whenever$X$and$Y$are infinite-dimensional Banach spaces. This was disproved byGilles Pisierin 1983. Pisier constructed an infinite-dimensional Banach space$X$such that$X{\widehat {\otimes }}_{\pi }X$and$X{\widehat {\otimes }}_{\varepsilon }X$are equal. Furthermore, just asEnflo'sexample, this space$X$is a "hand-made" space that fails to have the approximation property. On the other hand, Szankowski proved that the classical space$B\left(\ell ^{2}\right)$does not have the approximation property.

Some classification results

Characterizations of Hilbert space among Banach spaces

A necessary and sufficient condition for the norm of a Banach space$X$to be associated to an inner product is theparallelogram identity:

Parallelogram identity—for all$x,y\in X:\qquad \|x+y\|^{2}+\|x-y\|^{2}=2\left(\|x\|^{2}+\|y\|^{2}\right).$

It follows, for example, that theLebesgue space$L^{p}([0,1])$is a Hilbert space only when$p=2.$ If this identity is satisfied, the associated inner product is given by thepolarization identity.In the case of real scalars, this gives: $$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}\right).$$

For complex scalars, defining theinner productso as to be$\mathbb {C}$-linear in$x,$antilinearin$y,$the polarization identity gives: $$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}+i\left(\|x+iy\|^{2}-\|x-iy\|^{2}\right)\right).$$

To see that the parallelogram law is sufficient, one observes in the real case that$\langle x,y\rangle$is symmetric, and in the complex case, that it satisfies theHermitian symmetryproperty and$\langle ix,y\rangle =i\langle x,y\rangle.$The parallelogram law implies that$\langle x,y\rangle$is additive in$x.$ It follows that it is linear over the rationals, thus linear by continuity.

Several characterizations of spaces isomorphic (rather than isometric) to Hilbert spaces are available. The parallelogram law can be extended to more than two vectors, and weakened by the introduction of a two-sided inequality with a constant$c\geq 1$:Kwapień proved that if $$c^{-2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}\leq \operatorname {Ave} _{\pm }\left\|\sum _{k=1}^{n}\pm x_{k}\right\|^{2}\leq c^{2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}$$ for every integer$n$and all families of vectors$\left\{x_{1},\ldots,x_{n}\right\}\subseteq X,$then the Banach space$X$is isomorphic to a Hilbert space. Here,$\operatorname {Ave} _{\pm }$denotes the average over the$2^{n}$possible choices of signs$\pm 1.$ In the same article, Kwapień proved that the validity of a Banach-valuedParseval's theoremfor the Fourier transform characterizes Banach spaces isomorphic to Hilbert spaces.

Lindenstrauss and Tzafriri proved that a Banach space in which every closed linear subspace is complemented (that is, is the range of a bounded linear projection) is isomorphic to a Hilbert space.The proof rests uponDvoretzky's theoremabout Euclidean sections of high-dimensional centrally symmetric convex bodies. In other words, Dvoretzky's theorem states that for every integer$n,$any finite-dimensional normed space, with dimension sufficiently large compared to$n,$contains subspaces nearly isometric to the$n$-dimensional Euclidean space.

The next result gives the solution of the so-calledhomogeneous space problem.An infinite-dimensional Banach space$X$is said to behomogeneousif it is isomorphic to all its infinite-dimensional closed subspaces. A Banach space isomorphic to$\ell ^{2}$is homogeneous, and Banach asked for the converse.

Theorem—A Banach space isomorphic to all its infinite-dimensional closed subspaces is isomorphic to a separable Hilbert space.

An infinite-dimensional Banach space ishereditarily indecomposablewhen no subspace of it can be isomorphic to the direct sum of two infinite-dimensional Banach spaces. TheGowersdichotomy theoremasserts that every infinite-dimensional Banach space$X$contains, either a subspace$Y$withunconditional basis,or a hereditarily indecomposable subspace$Z,$and in particular,$Z$is not isomorphic to its closed hyperplanes. If$X$is homogeneous, it must therefore have an unconditional basis. It follows then from the partial solution obtained by Komorowski andTomczak–Jaegermann,for spaces with an unconditional basis,that$X$is isomorphic to$\ell ^{2}.$

Metric classification

If$T:X\to Y$is anisometryfrom the Banach space$X$onto the Banach space$Y$(where both$X$and$Y$are vector spaces over$\mathbb {R}$), then theMazur–Ulam theoremstates that$T$must be an affine transformation. In particular, if$T(0_{X})=0_{Y},$this is$T$maps the zero of$X$to the zero of$Y,$then$T$must be linear. This result implies that the metric in Banach spaces, and more generally in normed spaces, completely captures their linear structure.

Topological classification

Finite dimensional Banach spaces are homeomorphic as topological spaces, if and only if they have the same dimension as real vector spaces.

Anderson–Kadec theorem(1965–66) provesthat any two infinite-dimensionalseparableBanach spaces are homeomorphic as topological spaces. Kadec's theorem was extended by Torunczyk, who provedthat any two Banach spaces are homeomorphic if and only if they have the samedensity character,the minimum cardinality of a dense subset.

Spaces of continuous functions

When two compact Hausdorff spaces$K_{1}$and$K_{2}$arehomeomorphic,the Banach spaces$C\left(K_{1}\right)$and$C\left(K_{2}\right)$are isometric. Conversely, when$K_{1}$is not homeomorphic to$K_{2},$the (multiplicative) Banach–Mazur distance between$C\left(K_{1}\right)$and$C\left(K_{2}\right)$must be greater than or equal to$2,$see above theresults by Amir and Cambern. Although uncountable compact metric spaces can have different homeomorphy types, one has the following result due to Milutin:

Theorem—Let$K$be an uncountable compact metric space. Then$C(K)$is isomorphic to$C([0,1]).$

The situation is different forcountably infinitecompact Hausdorff spaces. Every countably infinite compact$K$is homeomorphic to some closed interval ofordinal numbers $$\langle 1,\alpha \rangle =\{\gamma \:\ 1\leq \gamma \leq \alpha \}$$ equipped with theorder topology,where$\alpha$is a countably infinite ordinal. The Banach space$C(K)$is then isometric toC(⟨1,α⟩).When$\alpha,\beta$are two countably infinite ordinals, and assuming$\alpha \leq \beta,$the spacesC(⟨1,α⟩)andC(⟨1,β⟩)are isomorphic if and only ifβ<α^ω. For example, the Banach spaces $$C(\langle 1,\omega \rangle ),\ C(\langle 1,\omega ^{\omega }\rangle ),\ C(\langle 1,\omega ^{\omega ^{2}}\rangle ),\ C(\langle 1,\omega ^{\omega ^{3}}\rangle ),\cdots,C(\langle 1,\omega ^{\omega ^{\omega }}\rangle ),\cdots$$ are mutually non-isomorphic.

Examples

Main article:List of Banach spaces

Glossary of symbols for the table below:

• $\mathbb {F}$denotes thefieldofreal numbers$\mathbb {R}$orcomplex numbers$\mathbb {C}.$
• $K$is acompact Hausdorff space.
• $p,q\in \mathbb {R}$arereal numberswith$1<p,q<\infty$that areHölder conjugates,meaning that they satisfy${\frac {1}{q}}+{\frac {1}{p}}=1$and thus also$q={\frac {p}{p-1}}.$
• $\Sigma$is a$\sigma$-algebraof sets.
• $\Xi$is analgebraof sets (for spaces only requiring finite additivity, such as theba space).
• $\mu$is ameasurewithvariation$|\mu |.$A positive measure is a real-valued positive set function defined on a$\sigma$-algebra which is countably additive.

ClassicalBanach spaces
	Dual space	Reflexive	weakly sequentially complete	Norm		Notes
$\mathbb {F} ^{n}$	$\mathbb {F} ^{n}$	Yes	Yes	$\|x\|_{2}$	$=\left(\sum _{i=1}^{n}|x_{i}|^{2}\right)^{1/2}$	Euclidean space
$\ell _{p}^{n}$	$\ell _{q}^{n}$	Yes	Yes	$\|x\|_{p}$	$=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{\frac {1}{p}}$
$\ell _{\infty }^{n}$	$\ell _{1}^{n}$	Yes	Yes	$\|x\|_{\infty }$	$=\max \nolimits _{1\leq i\leq n}|x_{i}|$
$\ell ^{p}$	$\ell ^{q}$	Yes	Yes	$\|x\|_{p}$	$=\left(\sum _{i=1}^{\infty }|x_{i}|^{p}\right)^{\frac {1}{p}}$
$\ell ^{1}$	$\ell ^{\infty }$	No	Yes	$\|x\|_{1}$	$=\sum _{i=1}^{\infty }\left|x_{i}\right|$
$\ell ^{\infty }$	$\operatorname {ba}$	No	No	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$
$\operatorname {c}$	$\ell ^{1}$	No	No	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$
$c_{0}$	$\ell ^{1}$	No	No	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$	Isomorphic but not isometric to$c.$
$\operatorname {bv}$	$\ell ^{\infty }$	No	Yes	$\|x\|_{bv}$	$=\left|x_{1}\right|+\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|$	Isometrically isomorphic to$\ell ^{1}.$
$\operatorname {bv} _{0}$	$\ell ^{\infty }$	No	Yes	$\|x\|_{bv_{0}}$	$=\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|$	Isometrically isomorphic to$\ell ^{1}.$
$\operatorname {bs}$	$\operatorname {ba}$	No	No	$\|x\|_{bs}$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|$	Isometrically isomorphic to$\ell ^{\infty }.$
$\operatorname {cs}$	$\ell ^{1}$	No	No	$\|x\|_{bs}$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|$	Isometrically isomorphic to$c.$
$B(K,\Xi )$	$\operatorname {ba} (\Xi )$	No	No	$\|f\|_{B}$	$=\sup \nolimits _{k\in K}|f(k)|$
$C(K)$	$\operatorname {rca} (K)$	No	No	$\|x\|_{C(K)}$	$=\max \nolimits _{k\in K}|f(k)|$
$\operatorname {ba} (\Xi )$	?	No	Yes	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Xi }|\mu |(S)$
$\operatorname {ca} (\Sigma )$	?	No	Yes	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$	A closed subspace of$\operatorname {ba} (\Sigma ).$
$\operatorname {rca} (\Sigma )$	?	No	Yes	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$	A closed subspace of$\operatorname {ca} (\Sigma ).$
$L^{p}(\mu )$	$L^{q}(\mu )$	Yes	Yes	$\|f\|_{p}$	$=\left(\int |f|^{p}\,d\mu \right)^{\frac {1}{p}}$
$L^{1}(\mu )$	$L^{\infty }(\mu )$	No	Yes	$\|f\|_{1}$	$=\int |f|\,d\mu$	The dual is$L^{\infty }(\mu )$if$\mu$is$\sigma$-finite.
$\operatorname {BV} ([a,b])$	?	No	Yes	$\|f\|_{BV}$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)$	$V_{f}([a,b])$is thetotal variationof$f$
$\operatorname {NBV} ([a,b])$	?	No	Yes	$\|f\|_{BV}$	$=V_{f}([a,b])$	$\operatorname {NBV} ([a,b])$consists of$\operatorname {BV} ([a,b])$functions such that$\lim \nolimits _{x\to a^{+}}f(x)=0$
$\operatorname {AC} ([a,b])$	$\mathbb {F} +L^{\infty }([a,b])$	No	Yes	$\|f\|_{BV}$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)$	Isomorphic to theSobolev space$W^{1,1}([a,b]).$
$C^{n}([a,b])$	$\operatorname {rca} ([a,b])$	No	No	$\|f\|$	$=\sum _{i=0}^{n}\sup \nolimits _{x\in [a,b]}\left|f^{(i)}(x)\right|$	Isomorphic to$\mathbb {R} ^{n}\oplus C([a,b]),$essentially byTaylor's theorem.

Derivatives

Several concepts of a derivative may be defined on a Banach space. See the articles on theFréchet derivativeand theGateaux derivativefor details. The Fréchet derivative allows for an extension of the concept of atotal derivativeto Banach spaces. The Gateaux derivative allows for an extension of adirectional derivativetolocally convextopological vector spaces. Fréchet differentiability is a stronger condition than Gateaux differentiability. Thequasi-derivativeis another generalization of directional derivative that implies a stronger condition than Gateaux differentiability, but a weaker condition than Fréchet differentiability.

Generalizations

Several important spaces in functional analysis, for instance the space of all infinitely often differentiable functions$\mathbb {R} \to \mathbb {R},$or the space of alldistributionson$\mathbb {R},$are complete but are not normed vector spaces and hence not Banach spaces. InFréchet spacesone still has a completemetric,whileLF-spacesare completeuniformvector spaces arising as limits of Fréchet spaces.

See also

• Space (mathematics)– Mathematical set with some added structure
  • Fréchet space– A locally convex topological vector space that is also a complete metric space
  • Hardy space– Concept within complex analysis
  • Hilbert space– Type of topological vector space
  • L-semi-inner product– Generalization of inner products that applies to all normed spaces
  • $L^{p}$space– Function spaces generalizing finite-dimensional p norm spaces
  • Sobolev space– Vector space of functions in mathematics
  • Banach lattice– Banach space with a compatible structure of a lattice
• Banach disk
• Banach manifold– Manifold modeled on Banach spaces
  • Banach bundle– vector bundle whose fibres form Banach spacesPages displaying wikidata descriptions as a fallback
• Distortion problem
• Interpolation space
• Locally convex topological vector space– A vector space with a topology defined by convex open sets
• Modulus and characteristic of convexity
• Smith space– complete compactly generated locally convex space having a universal compact setPages displaying wikidata descriptions as a fallback
• Topological vector space– Vector space with a notion of nearness
• Tsirelson space

Bibliography

• Aliprantis, Charalambos D.;Border, Kim C.(2006).Infinite Dimensional Analysis: A Hitchhiker's Guide(Third ed.). Berlin: Springer Science & Business Media.ISBN978-3-540-29587-7.OCLC262692874.
• Anderson, R. D.; Schori, R. (1969)."Factors of infinite-dimensional manifolds"(PDF).Transactions of the American Mathematical Society.142.American Mathematical Society (AMS): 315–330.doi:10.1090/s0002-9947-1969-0246327-5.ISSN0002-9947.
• Bachman, George; Narici, Lawrence (2000).Functional Analysis(Second ed.). Mineola, New York: Dover Publications.ISBN978-0486402512.OCLC829157984.
• Banach, Stefan(1932).Théorie des Opérations Linéaires[Theory of Linear Operations](PDF).Monografie Matematyczne (in French). Vol. 1. Warszawa: Subwencji Funduszu Kultury Narodowej.Zbl0005.20901.Archived fromthe original(PDF)on 2014-01-11.Retrieved2020-07-11.
• Beauzamy, Bernard (1985) [1982],Introduction to Banach Spaces and their Geometry(Second revised ed.), North-Holland.*Bourbaki, Nicolas(1987) [1981].Topological Vector Spaces: Chapters 1–5.Éléments de mathématique.Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag.ISBN3-540-13627-4.OCLC17499190.
• Bessaga, C.; Pełczyński, A. (1975),Selected Topics in Infinite-Dimensional Topology,Monografie Matematyczne, Warszawa: Panstwowe wyd. naukowe.
• Carothers, Neal L. (2005),A short course on Banach space theory,London Mathematical Society Student Texts, vol. 64, Cambridge: Cambridge University Press, pp. xii+184,ISBN0-521-84283-2.
• Conway, John(1990).A course in functional analysis.Graduate Texts in Mathematics.Vol. 96 (2nd ed.). New York:Springer-Verlag.ISBN978-0-387-97245-9.OCLC21195908.
• Diestel, Joseph (1984),Sequences and series in Banach spaces,Graduate Texts in Mathematics, vol. 92, New York: Springer-Verlag, pp.xii+261,ISBN0-387-90859-5.
• Dunford, Nelson; Schwartz, Jacob T. with the assistance of W. G. Bade and R. G. Bartle (1958),Linear Operators. I. General Theory,Pure and Applied Mathematics, vol. 7, New York: Interscience Publishers, Inc.,MR0117523
• Edwards, Robert E. (1995).Functional Analysis: Theory and Applications.New York: Dover Publications.ISBN978-0-486-68143-6.OCLC30593138.
• Grothendieck, Alexander(1973).Topological Vector Spaces.Translated by Chaljub, Orlando. New York: Gordon and Breach Science Publishers.ISBN978-0-677-30020-7.OCLC886098.
• Henderson, David W. (1969)."Infinite-dimensional manifolds are open subsets of Hilbert space".Bull. Amer. Math. Soc.75(4): 759–762.doi:10.1090/S0002-9904-1969-12276-7.MR0247634.
• Khaleelulla, S. M. (1982).Counterexamples in Topological Vector Spaces.Lecture Notes in Mathematics.Vol. 936. Berlin, Heidelberg, New York:Springer-Verlag.ISBN978-3-540-11565-6.OCLC8588370.
• Lindenstrauss, Joram;Tzafriri, Lior (1977),Classical Banach Spaces I, Sequence Spaces,Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 92, Berlin: Springer-Verlag,ISBN3-540-08072-4.
• Megginson, Robert E.(1998),An introduction to Banach space theory,Graduate Texts in Mathematics, vol. 183, New York: Springer-Verlag, pp. xx+596,ISBN0-387-98431-3.
• Narici, Lawrence; Beckenstein, Edward (2011).Topological Vector Spaces.Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press.ISBN978-1584888666.OCLC144216834.
• Riesz, Frederic;Sz.-Nagy, Béla(1990) [1955].Functional Analysis.Translated by Boron, Leo F. New York:Dover Publications.ISBN0-486-66289-6.OCLC21228994.
• Rudin, Walter(1991).Functional Analysis.International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY:McGraw-Hill Science/Engineering/Math.ISBN978-0-07-054236-5.OCLC21163277.
• Ryan, Raymond A. (2002),Introduction to Tensor Products of Banach Spaces,Springer Monographs in Mathematics, London: Springer-Verlag, pp. xiv+225,ISBN1-85233-437-1.
• Schaefer, Helmut H.;Wolff, Manfred P. (1999).Topological Vector Spaces.GTM.Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer.ISBN978-1-4612-7155-0.OCLC840278135.
• Swartz, Charles (1992).An introduction to Functional Analysis.New York: M. Dekker.ISBN978-0-8247-8643-4.OCLC24909067.
• Trèves, François(2006) [1967].Topological Vector Spaces, Distributions and Kernels.Mineola, N.Y.: Dover Publications.ISBN978-0-486-45352-1.OCLC853623322.
• Wilansky, Albert(2013).Modern Methods in Topological Vector Spaces.Mineola, New York: Dover Publications, Inc.ISBN978-0-486-49353-4.OCLC849801114.
• Wojtaszczyk, Przemysław (1991),Banach spaces for analysts,Cambridge Studies in Advanced Mathematics, vol. 25, Cambridge: Cambridge University Press, pp. xiv+382,ISBN0-521-35618-0.

External links

• "Banach space",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Weisstein, Eric W."Banach Space".MathWorld.