Ingeometry,abigon,[1]digon,or a2-gon,is apolygonwith two sides (edges) and twovertices.Its construction isdegeneratein aEuclidean planebecause either the two sides would coincide or one or both would have to be curved; however, it can be easily visualised inelliptic space.It may also be viewed as a representation of agraphwith two vertices, see "Generalized polygon".
| Regular digon | |
|---|---|
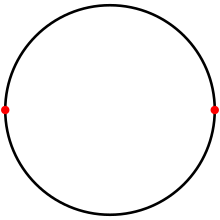 On a circle, adigonis atessellationwith twoantipodal points,and two 180° arc edges. | |
| Type | Regular polygon |
| Edgesandvertices | 2 |
| Schläfli symbol | {2} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | D2,[2], (*2•) |
| Internal angle(degrees) | 0° (convex) |
| Dual polygon | Self-dual |
A regular digon has both angles equal and both sides equal and is represented bySchläfli symbol{2}. It may be constructed on asphereas a pair of 180 degree arcs connectingantipodal points,when it forms alune.
The digon is the simplestabstract polytopeof rank 2.
Atruncateddigon,t{2} is asquare,{4}. Analternateddigon, h{2} is amonogon,{1}.
In different fields
editIn Euclidean geometry
editThe digon can have one of two visual representations if placed in Euclidean space.
One representation is degenerate, and visually appears as a double-covering of aline segment.Appearing when the minimum distance between the two edges is 0, this form arises in several situations. This double-covering form is sometimes used for defining degenerate cases of some other polytopes; for example, aregular tetrahedroncan be seen as anantiprismformed of such a digon. It can be derived from the alternation of a square (h{4}), as it requires two opposing vertices of said square to be connected. When higher-dimensional polytopes involving squares or other tetragonal figures are alternated, these digons are usually discarded and considered single edges.
A second visual representation, infinite in size, is as two parallel lines stretching to (and projectively meeting at; i.e. having vertices at) infinity, arising when the shortest distance between the two edges is greater than zero. This form arises in the representation of some degenerate polytopes, a notable example being theapeirogonal hosohedron,the limit of a general sphericalhosohedronat infinity, composed of an infinite number of digons meeting at two antipodal points at infinity.[2]However, as the vertices of these digons are at infinity and hence are not bound by closed line segments, this tessellation is usually not considered to be an additional regular tessellation of the Euclidean plane, even when its dualorder-2 apeirogonal tiling(infinite dihedron) is.
-
A compound of two "line segment" digons, as the two possible alternations of a square (note thevertex arrangement).
-
The apeirogonalhosohedron,containing infinitely narrow digons.
Any straight-sideddigonisregulareven though it is degenerate, because its two edges are the same length and its two angles are equal (both being zero degrees). As such, the regular digon is aconstructible polygon.[3]
Some definitions of a polygon do not consider the digon to be a proper polygon because of its degeneracy in the Euclidean case.[4]
In elementary polyhedra
editA digon as afaceof apolyhedronisdegeneratebecause it is a degenerate polygon, but sometimes it can have a useful topological existence in transforming polyhedra.
As a spherical lune
editAspherical luneis a digon whose two vertices areantipodal pointson the sphere.[5]
Aspherical polyhedronconstructed from such digons is called ahosohedron.
-
A lune on the sphere.
-
Six digon faces on a regular hexagonalhosohedron.
In topological structures
editDigons (bigons) may be used in constructing and analyzing various topological structures,[6]such asincidence structures.
See also
editReferences
editCitations
edit- ^"ResearchGate".
- ^The Symmetries of Things2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss,ISBN978-1-56881-220-5,p. 263
- ^Eric T. Eekhoff;Constructibility of Regular PolygonsArchived2015-07-14 at theWayback Machine,Iowa State University. (retrieved 20 December 2015)
- ^Coxeter (1973), Chapter 1,Polygons and Polyhedra,p.4
- ^Coxeter (1973), Chapter 1,Polygons and Polyhedra,pages 4 and 12.
- ^abAlex Degtyarev,Topology of Algebraic Curves: An Approach via Dessins d'Enfants,p. 263
Bibliography
edit- Herbert Busemann,The geometry of geodesics. New York, Academic Press, 1955
- Coxeter,Regular Polytopes(third edition), Dover Publications Inc, 1973ISBN0-486-61480-8
- Weisstein, Eric W."Digon".MathWorld.
- A.B. Ivanov (2001) [1994],"Digon",Encyclopedia of Mathematics,EMS Press
External links
edit- Media related toDigonsat Wikimedia Commons