Concyclic points

Ingeometry,asetofpointsare said to beconcyclic(orcocyclic) if they lie on a commoncircle.Apolygonwhoseverticesare concyclic is called acyclic polygon,and the circle is called itscircumscribing circleorcircumcircle.All concyclic points areequidistantfrom the center of the circle.

Concurrentperpendicular bisectors ofchordsbetween concyclic points

Circumscribed circle,C,and circumcenter,O,of acyclic polygon,P

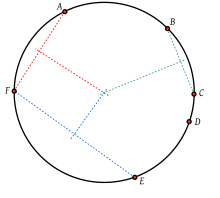
Three points in theplanethat do not all fall on astraight lineare concyclic, so everytriangleis a cyclic polygon, with a well-definedcircumcircle.However, four or more points in the plane are not necessarily concyclic. After triangles, the special case ofcyclic quadrilateralshas been most extensively studied.

Perpendicular bisectors

In general the centreOof a circle on which pointsPandQlie must be such thatOPandOQare equal distances. ThereforeOmust lie on theperpendicular bisectorof the line segmentPQ.Forndistinct points there aren(n− 1)/2bisectors, and the concyclic condition is that they all meet in a single point, the centreO.

Triangles

Main article:Circumcircle

The vertices of everytrianglefall on a circle called thecircumcircle.(Because of this, some authors define "concyclic" only in the context of four or more points on a circle.)Several other sets of points defined from a triangle are also concyclic, with different circles; seeNine-point circleandLester's theorem.

Theradiusof the circle on which lie a set of points is, by definition, the radius of the circumcircle of any triangle with vertices at any three of those points. If the pairwise distances among three of the points area,b,andc,then the circle's radius is

$R={\sqrt {\frac {a^{2}b^{2}c^{2}}{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}.$

The equation of the circumcircle of a triangle, and expressions for the radius and the coordinates of the circle's center, in terms of the Cartesian coordinates of the vertices are givenhere.

Other concyclic points

In any triangle all of the following nine points are concyclic on what is called thenine-point circle:the midpoints of the three edges, the feet of the threealtitudes,and the points halfway between theorthocenterand each of the three vertices.

Lester's theoremstates that in anyscalene triangle,the twoFermat points,thenine-point center,and thecircumcenterare concyclic.

Iflinesare drawn through theLemoine pointparallelto the sides of a triangle, then the six points of intersection of the lines and the sides of the triangle are concyclic, in what is called theLemoine circle.

Thevan Lamoen circleassociated with any given triangle$T$contains thecircumcentersof the six triangles that are defined inside$T$by its threemedians.

A triangle'scircumcenter,itsLemoine point,and its first twoBrocard pointsare concyclic, with the segment from the circumcenter to the Lemoine point being adiameter.

Cyclic quadrilaterals

Main article:Cyclic quadrilateral

Four concyclic points forming acyclic quadrilateral,showing two equal angles

A quadrilateralABCDwith concyclic vertices is called acyclic quadrilateral;this happensif and only if$\angle CAD=\angle CBD$(theinscribed angle theorem) which is true if and only if the opposite angles inside the quadrilateral aresupplementary.A cyclic quadrilateral with successive sidesa,b,c,dandsemiperimeters= (a+b+c+d) / 2 has its circumradius given by

$R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}},$

an expression that was derived by the Indian mathematician VatasseriParameshvarain the 15th century.

ByPtolemy's theorem,if a quadrilateral is given by the pairwise distances between its four verticesA,B,C,andDin order, then it is cyclic if and only if the product of the diagonals equals the sum of the products of opposite sides:

$AC\cdot BD=AB\cdot CD+BC\cdot AD.$

If two lines, one containing segmentACand the other containing segmentBD,intersect atX,then the four pointsA,B,C,Dare concyclic if and only if

$\displaystyle AX\cdot XC=BX\cdot XD.$

The intersectionXmay be internal or external to the circle. This theorem is known aspower of a point.

A convex quadrilateral isorthodiagonal(has perpendicular diagonals) if and only if the midpoints of the sides and the feet of the fouraltitudesare eight concyclic points, on what is called theeight-point circle.

Cyclic polygons

As a corollary of theannuluschord formula, the area bounded by thecircumcircleandincircleof every unit regularn-gon isπ/4

More generally, apolygonin which all vertices are concyclic is called acyclic polygon.A polygon is cyclic if and only if the perpendicular bisectors of its edges areconcurrent.Everyregular polygonis a cyclic polygon.

For a cyclic polygon with an odd number of sides, all angles are equal if and only if the polygon is regular. A cyclic polygon with an even number of sides has all angles equal if and only if the alternate sides are equal (that is, sides1, 3, 5,…are equal, and sides2, 4, 6,…are equal).

A cyclicpentagonwithrationalsides and area is known as aRobbins pentagon.In all known cases, its diagonals also have rational lengths, though whether this is true for all possible Robbins pentagons is an unsolved problem.

In any cyclicn-gon with evenn,the sum of one set of alternate angles (the first, third, fifth, etc.) equals the sum of the other set of alternate angles. This can be proven by induction from then= 4case, in each case replacing a side with three more sides and noting that these three new sides together with the old side form a quadrilateral which itself has this property; the alternate angles of the latter quadrilateral represent the additions to the alternate angle sums of the previousn-gon.

Atangential polygonis one having aninscribed circletangent to each side of the polygon; these tangency points are thus concyclic on the inscribed circle. Let onen-gon be inscribed in a circle, and let anothern-gon be tangential to that circle at the vertices of the firstn-gon. Then from any pointPon the circle, the product of the perpendicular distances fromPto the sides of the firstn-gon equals the product of the perpendicular distances fromPto the sides of the secondn-gon.

Point on the circumcircle

Let a cyclicn-gon have verticesA₁,…,A_non the unit circle. Then for any pointMon the minor arcA₁A_n,the distances fromMto the vertices satisfy

${\begin{cases}{\overline {MA_{1}}}+{\overline {MA_{3}}}+\cdots +{\overline {MA_{n-2}}}+{\overline {MA_{n}}}<n/{\sqrt {2}}&{\text{if }}n{\text{ is odd}};\\{\overline {MA_{1}}}+{\overline {MA_{3}}}+\cdots +{\overline {MA_{n-3}}}+{\overline {MA_{n-1}}}\leq n/{\sqrt {2}}&{\text{if }}n{\text{ is even}}.\end{cases}}$

For a regularn-gon, if${\overline {MA_{i}}}$are the distances from any pointMon the circumcircle to the verticesA_i,then

$3({\overline {MA_{1}}}^{2}+{\overline {MA_{2}}}^{2}+\dots +{\overline {MA_{n}}}^{2})^{2}=2n({\overline {MA_{1}}}^{4}+{\overline {MA_{2}}}^{4}+\dots +{\overline {MA_{n}}}^{4}).$

Polygon circumscribing constant

A sequence of circumscribed polygons and circles.

Anyregular polygonis cyclic. Consider a unit circle, then circumscribe a regular triangle such that each side touches the circle. Circumscribe a circle, then circumscribe a square. Again circumscribe a circle, then circumscribe a regularpentagon,and so on. The radii of the circumscribed circles converge to the so-calledpolygon circumscribing constant

$\prod _{n=3}^{\infty }{\frac {1}{\cos \left({\frac {\pi }{n}}\right)}}=8.7000366\ldots.$

(sequenceA051762in theOEIS). The reciprocal of this constant is theKepler–Bouwkamp constant.

Variations

In contexts where lines are taken to be a type ofgeneralised circlewith infinite radius,collinear points(points along a single line) are considered to be concyclic. This point of view is helpful, for instance, when studyinginversion through a circleor more generallyMöbius transformations(geometric transformations generated by reflections and circle inversions), as these transformations preserve the concyclicity of points only in this extended sense.

In thecomplex plane(formed by viewing thereal and imaginary partsof acomplex numberas thexandyCartesian coordinatesof the plane), concyclicity has a particularly simple formulation: four points in the complex plane are either concyclic or collinear if and only if theircross-ratiois areal number.

Integer area and side lengths

Some cyclic polygons have the property that their area and all of their side lengths are positive integers. Triangles with this property are calledHeronian triangles;cyclic quadrilaterals with this property (and that the diagonals that connect opposite vertices have integer length) are calledBrahmagupta quadrilaterals;cyclic pentagons with this property are calledRobbins pentagons.More generally, versions of these cyclic polygons scaled by arational numberwill have area and side lengths that are rational numbers.

Letθ₁be the angle spanned by one side of the cyclic polygon as viewed from the center of the circumscribing circle. Similarly define thecentral anglesθ₂,...,θ_nfor the remainingn− 1sides. Every Heronian triangle and every Brahmagupta quadrilateral has a rational value for the tangent of the quarter angle,tanθ_k/4,for every value ofk.Every known Robbins pentagon (has diagonals that have rational length and) has this property, though it is an unsolved problem whether every possible Robbins pentagon has this property.

The reverse is true for all cyclic polygons with any number of sides; if all such central angles have rational tangents for their quarter angles then the implied cyclic polygon circumscribed by the unit circle will simultaneously have rational side lengths and rational area. Additionally, each diagonal that connects two vertices, whether or not the two vertices are adjacent, will have a rational length. Such a cyclic polygon can be scaled so that its area and lengths are all integers.

This reverse relationship gives a way to generate cyclic polygons with integer area, sides, and diagonals. For a polygon withnsides, let0 <c₁<... <c_n−1< +∞be rational numbers. These are the tangents of one quarter of the cumulative anglesθ₁,θ₁+θ₂,...,θ₁+... +θ_n−1.Letq₁=c₁,letq_n= 1 /c_n−1,and letq_k= (c_k−c_k−1) / (1 +c_kc_k−1)fork= 2,...,n−1.These rational numbers are the tangents of the individual quarter angles, using the formula for the tangent of the difference of angles. Rational side lengths for the polygon circumscribed by the unit circle are thus obtained ass_k= 4q_k/ (1 +q_k²).The rational area isA= ∑_k2q_k(1 −q_k²) / (1 +q_k²)².These can be made into integers by scaling the side lengths by a shared constant.

Other properties

A set of five or more points is concyclic if and only if every four-pointsubsetis concyclic.This property can be thought of as an analogue for concyclicity of theHelly propertyof convex sets.

Minimum bounding circle

A related notion is the one of aminimum bounding circle,which is the smallest circle that completely contains a set of points. Every set of points in the plane has a unique minimum bounding circle, which may be constructed by alinear timealgorithm.

Even if a set of points are concyclic, their circumscribing circle may be different from their minimum bounding circle. For example, for anobtuse triangle,the minimum bounding circle has the longest side as diameter and does not pass through the opposite vertex.

External links

• Weisstein, Eric W."Concyclic".MathWorld.
• Four Concyclic Pointsby Michael Schreiber,The Wolfram Demonstrations Project.