Diameter

For other uses, seeDiameter (disambiguation).

Ingeometry,adiameterof acircleis any straightline segmentthat passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longestchordof the circle. Both definitions are also valid for the diameter of asphere.

Circle with

circumferenceC

diameterD

radiusR

centre or originO

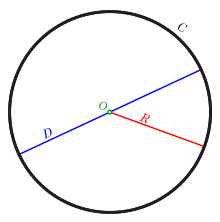
In more modern usage, the length$d$of a diameter is also called the diameter. In this sense one speaks ofthediameter rather thanadiameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice theradius$r.$

$d=2r\qquad {\text{or equivalently}}\qquad r={\frac {d}{2}}.$

For aconvexshape in theplane,the diameter is defined to be the largest distance that can be formed between two oppositeparallel linestangentto its boundary, and thewidthis often defined to be the smallest such distance. Both quantities can be calculated efficiently usingrotating calipers.For acurve of constant widthsuch as theReuleaux triangle,the width and diameter are the same because all such pairs of parallel tangent lines have the same distance.

For anellipse,the standard terminology is different. A diameter of an ellipse is anychordpassing through the centre of the ellipse.For example,conjugate diametershave the property that a tangent line to the ellipse at the endpoint of one diameter is parallel to the conjugate diameter. The longest diameter is called themajor axis.

The word "diameter" is derived fromAncient Greek:διάμετρος(diametros), "diameter of a circle", fromδιά(dia), "across, through" andμέτρον(metron), "measure".It is often abbreviated${\text{DIA}},{\text{dia}},d,$or$\varnothing.$

Generalizations

See also:Metric space § Diameter of a metric space

The definitions given above are only valid for circles, spheres and convex shapes. However, they are special cases of a more general definition that is valid for any kind of$n$-dimensional (convex or non-convex) object, such as ahypercubeor asetof scattered points. Thediameterormetric diameterof asubsetof ametric spaceis theleast upper boundof the set of all distances between pairs of points in the subset. Explicitly, if$S$is the subset and if$\rho$is themetric,the diameter is $$\operatorname {diam} (S)=\sup _{x,y\in S}\rho (x,y).$$

If the metric$\rho$is viewed here as havingcodomain$\mathbb {R}$(the set of allreal numbers), this implies that the diameter of theempty set(the case$S=\varnothing$) equals$-\infty$(negative infinity). Some authors prefer to treat the empty set as a special case, assigning it a diameter of$0,$which corresponds to taking the codomain of$\rho$to be the set of nonnegative reals.

For any solid object or set of scattered points in$n$-dimensionalEuclidean space,the diameter of the object or set is the same as the diameter of itsconvex hull.In medical terminology concerning a lesion or in geology concerning a rock, the diameter of an object is the least upper bound of the set of all distances between pairs of points in the object.

Indifferential geometry,the diameter is an important globalRiemannianinvariant.

Inplanar geometry,a diameter of aconic sectionis typically defined as any chord which passes through theconic's centre;such diameters are not necessarily of uniform length, except in the case of the circle, which haseccentricity$e=0.$

Symbol

"⌀" redirects here. For other uses, see⌀ (disambiguation).

Sign ⌀ in a technical drawing

Aphotographic filtermarked as having a 58mm thread diameter

Thesymbolorvariablefor diameter,⌀,is sometimes used in technical drawings or specifications as a prefix or suffix for a number (e.g. "⌀ 55 mm" ), indicating that it represents diameter.Photographicfilter threadsizes are often denoted in this way.

The symbol has acode pointinUnicodeatU+2300⌀DIAMETER SIGN,in theMiscellaneous Technicalset. It should not be confused with several other characters (such asU+00D8ØLATIN CAPITAL LETTER O WITH STROKEorU+2205∅EMPTY SET) that resemble it but have unrelated meanings.It has thecompose sequenceComposedi.

Diameter vs. radius

The diameter of a circle is exactly twice its radius. However, this is true only for a circle, and only in theEuclidean metric.Jung's theoremprovides more general inequalities relating the diameter to the radius.

See also

• Angular diameter– How large a sphere or circle appears
• Caliper,micrometer,tools for measuring diameters
• Conjugate diameters– Perpendicular diameters of a circle or hyperbolic-orthogonal diameters of a hyperbola
• Diameter (group theory)– Concept in group theory, a concept ingroup theory
• Equivalent diameter– Radius of a circle or sphere equivalent to a non-circular or non-spherical objectPages displaying short descriptions of redirect targets
• Eratosthenes,who calculated the diameter of theEartharound 240 BC.
• Graph or network diameter– Length of shortest path between two nodes of a graph
• Hydraulic diameter– Measure of a channel flow efficiency
• Inside diameter*Semidiameter– Term in geometry; half of a shape's diameter
• Sauter mean diameter– Average measure of particle size
• Tangent lines to circles– Line which touches a circle at exactly one point
• Thediameters of a screw thread