Displacement (geometry)

Ingeometryandmechanics,adisplacementis avectorwhose length is the shortestdistancefrom the initial to the finalpositionof a point P undergoingmotion.It quantifies both the distance anddirectionof the net or total motion along a straight line from the initial position to the final position of the pointtrajectory.A displacement may be identified with thetranslationthat maps the initial position to the final position. Displacement is the shift in location when an object in motion changes from one position to another. For motion over a given interval of time, the displacement divided by the length of the time interval defines theaverage velocity(a vector), whose magnitude is theaverage speed(a scalar quantity).

Displacement
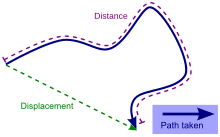Displacement versus distance travelled along a path
Common symbols	d
SI unit	metre
InSI base units	m
Dimension	L

Formulation

A displacement may be formulated as arelative position(resulting from the motion), that is, as the final positionx_fof a point relative to its initial positionx_i.The corresponding displacement vector can be defined as thedifferencebetween the final and initial positions: $$s=x_{\textrm {f}}-x_{\textrm {i}}=\Delta {x}$$

Rigid body

In dealing with the motion of arigid body,the termdisplacementmay also include therotationsof the body. In this case, the displacement of a particle of the body is calledlinear displacement(displacement along a line), while the rotation of the body is calledangular displacement.

Derivatives

See also:Position (geometry) § Derivatives

For a position vector$\mathbf {s}$that is a function of time$t$,the derivatives can be computed with respect to$t$.The first two derivatives are frequently encountered in physics.

Velocity

$\mathbf {v} ={\frac {d\mathbf {s} }{dt}}$

Acceleration

$\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {s} }{dt^{2}}}$

Jerk

$\mathbf {j} ={\frac {d\mathbf {a} }{dt}}={\frac {d^{2}\mathbf {v} }{dt^{2}}}={\frac {d^{3}\mathbf {s} }{dt^{3}}}$

These common names correspond to terminology used in basic kinematics.By extension, the higher order derivatives can be computed in a similar fashion. Study of these higher order derivatives can improve approximations of the original displacement function. Such higher-order terms are required in order to accurately represent the displacement function asa sum of an infinite series,enabling several analytical techniques in engineering and physics. The fourth order derivative is calledjounce.

Discussion

In considering motions of objects over time, the instantaneousvelocityof the object is the rate of change of the displacement as a function of time. The instantaneousspeed,then, is distinct from velocity, or thetime rateof change of the distance travelled along a specific path. The velocity may be equivalently defined as the time rate of change of the position vector. If one considers a moving initial position, or equivalently a moving origin (e.g. an initial position or origin which is fixed to a train wagon, which in turn moves on its rail track), the velocity of P (e.g. a point representing the position of a passenger walking on the train) may be referred to as arelative velocity;this is opposed to anabsolute velocity,which is computed with respect to a point and coordinate axes which are considered to be at rest (ainertial frame of referencesuch as, for instance, a point fixed on the floor of the train station and the usual vertical and horizontal directions).

See also

• Affine space
• Deformation (mechanics)
• Displacement field (mechanics)
• Equipollence (geometry)
• Motion vector
• Position vector
• Radial velocity
• Screw displacement

External links

• Media related toDisplacement vectorat Wikimedia Commons