Dodecagon

Regular dodecagon
Regular dodecagon
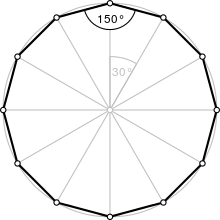	A regular dodecagon
Type	Regular polygon
Edgesandvertices	12
Schläfli symbol	{12}, t{6}, tt{3}
Coxeter–Dynkin diagrams	;
Symmetry group	Dihedral(D12), order 2×12
Internal angle(degrees)	150°
Properties	Convex,cyclic,equilateral,isogonal,isotoxal
Dual polygon	Self

Ingeometry,adodecagon,or12-gon,is any twelve-sidedpolygon.

Regular dodecagon

Three squares of sidesRcan be cut and rearranged into a dodecagon ofcircumradiusR,yielding aproof without wordsthat its area is 3R²

Aregulardodecagon is a figure with sides of the same length and internal angles of the same size. It has twelve lines of reflective symmetry and rotational symmetry of order 12. A regular dodecagon is represented by theSchläfli symbol{12} and can be constructed as atruncated hexagon,t{6}, or a twice-truncatedtriangle,tt{3}. The internal angle at each vertex of a regular dodecagon is 150°.

Area

Theareaof a regular dodecagon of side lengthais given by:

{\begin{aligned}A&=3\cot \left({\frac {\pi }{12}}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}\\&\simeq 11.19615242\,a^{2}\end{aligned}}

And in terms of theapothemr(see alsoinscribed figure), the area is:

{\begin{aligned}A&=12\tan \left({\frac {\pi }{12}}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}\\&\simeq 3.2153903\,r^{2}\end{aligned}}

In terms of thecircumradiusR,the area is:^[1]

A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2}

The spanSof the dodecagon is the distance between two parallel sides and is equal to twice the apothem. A simple formula for area (given side length and span) is:

A=3aS

This can be verified with the trigonometric relationship:

S=a(1+2\cos {30^{\circ }}+2\cos {60^{\circ }})

Perimeter

Theperimeterof a regular dodecagon in terms of circumradius is:^[2]

{\begin{aligned}p&=24R\tan \left({\frac {\pi }{12}}\right)=12R{\sqrt {2-{\sqrt {3}}}}\\&\simeq 6.21165708246\,R\end{aligned}}

The perimeter in terms of apothem is:

{\begin{aligned}p&=24r\tan \left({\frac {\pi }{12}}\right)=24r(2-{\sqrt {3}})\\&\simeq 6.43078061835\,r\end{aligned}}

This coefficient is double the coefficient found in the apothem equation for area.^[3]

Dodecagon construction

As 12 = 2²× 3, regular dodecagon isconstructibleusingcompass-and-straightedge construction:

Construction of a regular dodecagon at a givencircumcircle

Construction of a regular dodecagon
at a given side length, animation. (The construction is very similar to that ofoctagon at a given side length.)

Dissection

12-cube	60 rhomb dissection

Isotoxal dodecagon

Coxeterstates that everyzonogon(a 2m-gon whose opposite sides are parallel and of equal length) can be dissected intom(m-1)/2 parallelograms.^[4] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are allrhombi.For theregular dodecagon,m=6, and it can be divided into 15: 3 squares, 6 wide 30° rhombs and 6 narrow 15° rhombs. This decomposition is based on aPetrie polygonprojection of a6-cube,with 15 of 240 faces. The sequence OEIS sequenceA006245defines the number of solutions as 908, including up to 12-fold rotations and chiral forms in reflection.

Dissection into 15 rhombs
6-cube

One of the ways themathematical manipulative pattern blocksare used is in creating a number of different dodecagons.^[5]They are related to the rhombic dissections, with 3 60° rhombi merged into hexagons, half-hexagon trapezoids, or divided into 2 equilateral triangles.

Other regular dissections
		Socolar tiling	Pattern blocks

Symmetry

The symmetries of a regular dodecagon as shown with colors on edges and vertices.John Conwaylabels these lower symmetries with a letter and order of the symmetry follows the letter. He givesd(diagonal, diasymmetry) with mirror lines through vertices,pwith mirror lines through edges (perpendicular, persymmetry)iwith mirror lines through both vertices and edges (isosymmetry), andgfor rotational (gyrosymmetry).a1labels asymmetry. These lower symmetries allows degrees of freedoms in defining irregular dodecagons.^[6]

Theregular dodecagonhas Dih₁₂symmetry, order 24. There are 15 distinct subgroup dihedral and cyclic symmetries. Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only theg12subgroup has no degrees of freedom but can be seen asdirected edges.

Example dodecagons by symmetry
r24
d12	g12	p12	i8
d6	g6	p6	d4	g4	p4
g3			d2	g2	p2
a1

Occurrence

Tiling

A regular dodecagon canfill a plane vertexwith other regular polygons in 4 ways:

3.12.12	4.6.12	3.3.4.12	3.4.3.12

Here are 3 exampleperiodic plane tilingsthat use regular dodecagons, defined by theirvertex configuration:

1-uniform		2-uniform
3.12.12	4.6.12	3.12.12; 3.4.3.12

Skew dodecagon

A regular skew dodecagon seen as zig-zagging edges of ahexagonal antiprism.

Askew dodecagonis askew polygonwith 12 vertices and edges but not existing on the same plane. The interior of such a dodecagon is not generally defined. Askew zig-zag dodecagonhas vertices alternating between two parallel planes.

Aregular skew dodecagonisvertex-transitivewith equal edge lengths. In 3-dimensions it will be a zig-zag skew dodecagon and can be seen in the vertices and side edges of ahexagonal antiprismwith the same D_5d,[2⁺,10] symmetry, order 20. The dodecagrammic antiprism, s{2,24/5} and dodecagrammic crossed-antiprism, s{2,24/7} also have regular skew dodecagons.

Petrie polygons

The regular dodecagon is thePetrie polygonfor many higher-dimensional polytopes, seen asorthogonal projectionsinCoxeter planes.Examples in 4 dimensions are the24-cell,snub 24-cell,6-6 duoprism,6-6 duopyramid.In 6 dimensions6-cube,6-orthoplex,2₂₁,1₂₂.It is also the Petrie polygon for thegrand 120-cellandgreat stellated 120-cell.

Regular skew dodecagons in higher dimensions
E₆		F₄		2G₂(4D)
2₂₁	1₂₂	24-cell	Snub 24-cell	6-6 duopyramid	{6}×{6}
A₁₁	D₇		B₆		4A₂
11-simplex	(4₁₁)	1₄₁	6-orthoplex	6-cube	{3}×{3}×{3}×{3}

Related figures

Adodecagramis a 12-sided star polygon, represented by symbol {12/n}. There is one regularstar polygon:{12/5}, using the same vertices, but connecting every fifth point. There are also three compounds: {12/2} is reduced to 2{6} as twohexagons,and {12/3} is reduced to 3{4} as threesquares,{12/4} is reduced to 4{3} as four triangles, and {12/6} is reduced to 6{2} as six degeneratedigons.

Stars and compounds
n	1	2	3	4	5	6
Form	Polygon	Compounds			Star polygon	Compound
Image	{12/1} = {12}	{12/2} or 2{6}	{12/3} or 3{4}	{12/4} or 4{3}	{12/5}	{12/6} or 6{2}

Deeper truncations of the regular dodecagon and dodecagrams can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths. A truncated hexagon is a dodecagon, t{6}={12}. A quasitruncated hexagon, inverted as {6/5}, is a dodecagram: t{6/5}={12/5}.^[7]

Vertex-transitive truncations of the hexagon
Quasiregular	Isogonal		Quasiregular
t{6}={12}			t{6/5}={12/5}

Examples in use

Inblock capitals,the lettersE,HandX(andIin aslab seriffont) have dodecagonal outlines. Acrossis a dodecagon, as is the logo for theChevroletautomobile division.

The Vera Cruz church inSegovia

The regular dodecagon features prominently in many buildings. TheTorre del Orois a dodecagonal militarywatchtowerinSeville,southernSpain,built by theAlmohad dynasty.The early thirteenth century Vera Cruz church inSegovia,Spain is dodecagonal. Another example is the Porta di Venere (Venus' Gate), inSpello,Italy,built in the 1st century BC has two dodecagonal towers, called "Propertius' Towers".

A 1942 British threepence, reverse

Regulardodecagonal coinsinclude:

British threepenny bitfrom 1937 to 1971, when it ceased to be legal tender.
British One Pound Coin,introduced in 2017.
Australian 50-cent coin
Fi gian 50 cents
Tongan 50-seniti,since 1974
Solomon Islands 50 cents
Croatian 25 kuna
Romanian 5000 lei,2001–2005
Canadian penny,1982–1996
South Vietnamese 20 đồng,1968–1975
Zambian 50 ngwee,1969–1992
Malawian 50 tambala,1986–1995
Mexican 20 centavos,1992-2009

Notes

^See alsoKürschák's geometric proof onthe Wolfram Demonstration Project
^Plane Geometry: Experiment, Classification, Discovery, Applicationby Clarence Addison Willis B., (1922) Blakiston's Son & Company, p. 249[1]
^Elements of geometry byJohn Playfair,William Wallace, John Davidsons, (1814) Bell & Bradfute, p. 243[2]
^Coxeter,Mathematical recreations and Essays, Thirteenth edition, p.141
^"Doin' Da' Dodeca'" onmathforum.org
^John H. Conway, Heidi Burgiel,Chaim Goodman-Strauss,(2008) The Symmetries of Things,ISBN 978-1-56881-220-5(Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275–278)
^The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994),Metamorphoses of polygons,Branko Grünbaum

External links

Weisstein, Eric W."Dodecagon".MathWorld.
Kürschak's Tile and Theorem
Definition and properties of a dodecagonWith interactive animation
The regular dodecagon in the classroom,usingpattern blocks

[1] See alsoKürschák's geometric proof onthe Wolfram Demonstration Project

[2] Plane Geometry: Experiment, Classification, Discovery, Applicationby Clarence Addison Willis B., (1922) Blakiston's Son & Company, p. 249[1]

[3] Elements of geometry byJohn Playfair,William Wallace, John Davidsons, (1814) Bell & Bradfute, p. 243[2]

[4] Coxeter,Mathematical recreations and Essays, Thirteenth edition, p.141

[5] "Doin' Da' Dodeca'" onmathforum.org

[6] John H. Conway, Heidi Burgiel,Chaim Goodman-Strauss,(2008) The Symmetries of Things,ISBN 978-1-56881-220-5(Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275–278)

[7] The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994),Metamorphoses of polygons,Branko Grünbaum

[1]

[2]

[3]

[4]

[5]

[6]

[7]