Hypercube graph

Ingraph theory,thehypercube graphQ_nis the graph formed from the vertices and edges of ann-dimensionalhypercube.For instance, thecube graphQ₃is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Q_nhas2ⁿvertices,2^{n– 1}nedges, and is aregular graphwithnedges touching each vertex.

Hypercube graph
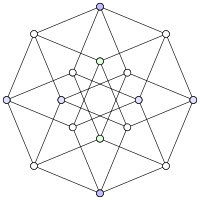The hypercube graphQ4
Vertices	2n
Edges	2n– 1n
Diameter	n
Girth	4ifn≥ 2
Automorphisms	n!2n
Chromatic number	2
Spectrum	$\{(n-2k)^{\binom {n}{k}};k=0,\ldots,n\}$
Properties	Symmetric Distance regular Unit distance Hamiltonian Bipartite
Notation	Qn
Table of graphs and parameters

The hypercube graphQ_nmay also be constructed by creating a vertex for eachsubsetof ann-element set, with two vertices adjacent when their subsets differ in a single element, or by creating a vertex for eachn-digitbinary number,with two vertices adjacent when their binary representations differ in a single digit. It is then-foldCartesian productof the two-vertexcomplete graph,and may be decomposed into two copies ofQ_{n– 1}connected to each other by aperfect matching.

Hypercube graphs should not be confused withcubic graphs,which are graphs that have exactly three edges touching each vertex. The only hypercube graphQ_nthat is a cubic graph is the cubical graphQ₃.

Construction

Construction ofQ₃by connecting pairs of corresponding vertices in two copies ofQ₂

The hypercube graphQ_nmay be constructed from the family ofsubsetsof asetwithnelements, by making a vertex for each possible subset and joining two vertices by an edge whenever the corresponding subsets differ in a single element. Equivalently, it may be constructed using2ⁿvertices labeled withn-bitbinary numbersand connecting two vertices by an edge whenever theHamming distanceof their labels is one. These two constructions are closely related: a binary number may be interpreted as a set (the set of positions where it has a1digit), and two such sets differ in a single element whenever the corresponding two binary numbers have Hamming distance one.

Alternatively,Q_nmay be constructed from thedisjoint unionof two hypercubesQ_{n− 1},by adding an edge from each vertex in one copy ofQ_{n− 1}to the corresponding vertex in the other copy, as shown in the figure. The joining edges form aperfect matching.

The above construction gives a recursive algorithm for constructing theadjacency matrixof a hypercube,A_n.Copying is done via theKronecker product,so that the two copies ofQ_{n− 1}have an adjacency matrix$\mathrm {1} _{2}\otimes _{K}A_{n-1}$,where$1_{d}$is theidentity matrixin$d$dimensions. Meanwhile the joining edges have an adjacency matrix$A_{1}\otimes _{K}1_{2^{n-1}}$.The sum of these two terms gives a recursive function function for the adjacency matrix of a hypercube:

$A_{n}={\begin{cases}1_{2}\otimes _{K}A_{n-1}+A_{1}\otimes _{K}1_{2^{n-1}}&{\text{if }}n>1\\{\begin{bmatrix}0&1\\1&0\end{bmatrix}}&{\text{if }}n=1\end{cases}}$

Another construction ofQ_nis theCartesian productofntwo-vertex complete graphsK₂.More generally the Cartesian product of copies of a complete graph is called aHamming graph;the hypercube graphs are examples of Hamming graphs.

Examples

The graphQ₀consists of a single vertex, whileQ₁is thecomplete graphon two vertices.

Q₂is acycleof length4.

The graphQ₃is the1-skeletonof acubeand is a planar graph with eightverticesand twelveedges.

The graphQ₄is theLevi graphof theMöbius configuration.It is also theknight's graphfor atoroidal$4\times 4$chessboard.

Properties

Bipartiteness

Every hypercube graph isbipartite:it can becoloredwith only two colors. The two colors of this coloring may be found from the subset construction of hypercube graphs, by giving one color to the subsets that have an even number of elements and the other color to the subsets with an odd number of elements.

Hamiltonicity

A Hamiltonian cycle on a tesseract with vertices labelled with a 4-bit cyclic Gray code

Every hypercubeQ_nwithn> 1has aHamiltonian cycle,a cycle that visits each vertex exactly once. Additionally, aHamiltonian pathexists between two verticesuandvif and only if they have different colors in a2-coloring of the graph. Both facts are easy to prove using the principle ofinductionon the dimension of the hypercube, and the construction of the hypercube graph by joining two smaller hypercubes with a matching.

Hamiltonicity of the hypercube is tightly related to the theory ofGray codes.More precisely there is abijectivecorrespondence between the set ofn-bit cyclic Gray codes and the set of Hamiltonian cycles in the hypercubeQ_n.An analogous property holds for acyclicn-bit Gray codes and Hamiltonian paths.

A lesser known fact is that every perfect matching in the hypercube extends to a Hamiltonian cycle.The question whether every matching extends to a Hamiltonian cycle remains an open problem.

Other properties

The hypercube graphQ_n(forn> 1):

• is theHasse diagramof a finiteBoolean algebra.
• is amedian graph.Every median graph is anisometric subgraph of a hypercube,and can be formed as a retraction of a hypercube.
• has more than2^2n-2perfect matchings. (this is another consequence that follows easily from the inductive construction.)
• isarc transitiveandsymmetric.The symmetries of hypercube graphs can be represented assigned permutations.
• contains all the cycles of length4, 6,..., 2ⁿand is thus abipancyclic graph.
• can bedrawnas aunit distance graphin the Euclidean plane by using the construction of the hypercube graph from subsets of a set ofnelements, choosing a distinctunit vectorfor each set element, and placing the vertex corresponding to the setSat the sum of the vectors inS.
• is an-vertex-connected graph,byBalinski's theorem.
• isplanar(can bedrawnwith no crossings) if and only ifn≤ 3.For larger values ofn,the hypercube hasgenus(n− 4)2^{n− 3}+ 1.
• has exactly$2^{2^{n}-n-1}\prod _{k=2}^{n}k^{n \choose k}$spanning trees.
• hasbandwidthexactly$\sum _{i=0}^{n-1}{\binom {i}{\lfloor i/2\rfloor }}$.
• hasachromatic numberproportional to${\sqrt {n2^{n}}}$,but the constant of proportionality is not known precisely.
• has as the eigenvalues of itsadjacency matrixthe numbers(−n,−n+ 2, −n+ 4,...,n− 4,n− 2,n)and as the eigenvalues of its Laplacian matrix the numbers(0, 2,..., 2n).Thekth eigenvalue has multiplicity${\binom {n}{k}}$in both cases.
• hasisoperimetric numberh(G) = 1.

The familyQ_nfor alln> 1is aLévy family of graphs.

Problems

Maximum lengths of snakes (L_s) and coils (L_c) in the snakes-in-the-box problem for dimensionsnfrom 1 to 4

The problem of finding thelongest pathor cycle that is aninduced subgraphof a given hypercube graph is known as thesnake-in-the-boxproblem.

Szymanski's conjectureconcerns the suitability of a hypercube as anetwork topologyfor communications. It states that, no matter how one chooses apermutationconnecting each hypercube vertex to another vertex with which it should be connected, there is always a way to connect these pairs of vertices bypathsthat do not share any directed edge.

See also

• de Bruijn graph
• Cube-connected cycles
• Fibonacci cube
• Folded cube graph
• Frankl–Rödl graph
• Halved cube graph
• Hypercube internetwork topology
• Partial cube

References

• Harary, F.;Hayes, J. P.; Wu, H.-J. (1988), "A survey of the theory of hypercube graphs",Computers & Mathematics with Applications,15(4): 277–289,doi:10.1016/0898-1221(88)90213-1,hdl:2027.42/27522.