Matrix multiplication

Inmathematics,specifically inlinear algebra,matrix multiplicationis abinary operationthat produces amatrixfrom two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as thematrix product,has the number of rows of the first and the number of columns of the second matrix. The product of matricesAandBis denoted asAB.

For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The result matrix has the number of rows of the first and the number of columns of the second matrix.

Matrix multiplication was first described by the French mathematicianJacques Philippe Marie Binetin 1812,to represent thecompositionoflinear mapsthat are represented by matrices. Matrix multiplication is thus a basic tool oflinear algebra,and as such has numerous applications in many areas of mathematics, as well as inapplied mathematics,statistics,physics,economics,andengineering. Computing matrix products is a central operation in all computational applications of linear algebra.

Notation

This article will use the following notational conventions: matrices are represented by capital letters in bold, e.g.A;vectorsin lowercase bold, e.g.a;and entries of vectors and matrices are italic (they are numbers from a field), e.g.Aanda.Index notationis often the clearest way to express definitions, and is used as standard in the literature. The entry in rowi,columnjof matrixAis indicated by(A)_ij,A_ijora_ij.In contrast, a single subscript, e.g.A₁,A₂,is used to select a matrix (not a matrix entry) from a collection of matrices.

Definitions

Matrix times matrix

IfAis anm×nmatrix andBis ann×pmatrix, $$\mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}b_{11}&b_{12}&\cdots &b_{1p}\\b_{21}&b_{22}&\cdots &b_{2p}\\\vdots &\vdots &\ddots &\vdots \\b_{n1}&b_{n2}&\cdots &b_{np}\\\end{pmatrix}}$$ thematrix productC=AB(denoted without multiplication signs or dots) is defined to be them×pmatrix $$\mathbf {C} ={\begin{pmatrix}c_{11}&c_{12}&\cdots &c_{1p}\\c_{21}&c_{22}&\cdots &c_{2p}\\\vdots &\vdots &\ddots &\vdots \\c_{m1}&c_{m2}&\cdots &c_{mp}\\\end{pmatrix}}$$ such that $$c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}=\sum _{k=1}^{n}a_{ik}b_{kj},$$ fori= 1,...,mandj= 1,...,p.

That is, the entry⁠$c_{ij}$⁠of the product is obtained by multiplying term-by-term the entries of theith row ofAand thejth column ofB,and summing thesenproducts. In other words,⁠$c_{ij}$⁠is thedot productof theith row ofAand thejth column ofB.

Therefore,ABcan also be written as $$\mathbf {C} ={\begin{pmatrix}a_{11}b_{11}+\cdots +a_{1n}b_{n1}&a_{11}b_{12}+\cdots +a_{1n}b_{n2}&\cdots &a_{11}b_{1p}+\cdots +a_{1n}b_{np}\\a_{21}b_{11}+\cdots +a_{2n}b_{n1}&a_{21}b_{12}+\cdots +a_{2n}b_{n2}&\cdots &a_{21}b_{1p}+\cdots +a_{2n}b_{np}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}b_{11}+\cdots +a_{mn}b_{n1}&a_{m1}b_{12}+\cdots +a_{mn}b_{n2}&\cdots &a_{m1}b_{1p}+\cdots +a_{mn}b_{np}\\\end{pmatrix}}$$

Thus the productABis defined if and only if the number of columns inAequals the number of rows inB,in this casen.

In most scenarios, the entries are numbers, but they may be any kind ofmathematical objectsfor which an addition and a multiplication are defined, that areassociative,and such that the addition iscommutative,and the multiplication isdistributivewith respect to the addition. In particular, the entries may be matrices themselves (seeblock matrix).

Matrix times vector

A vector$\mathbf {x}$of length$n$can be viewed as acolumn vector,corresponding to an$n\times 1$matrix$\mathbf {X}$whose entries are given by$\mathbf {X} _{i1}=\mathbf {x} _{i}.$If$\mathbf {A}$is an$m\times n$matrix, the matrix-times-vector product denoted by$\mathbf {Ax}$is then the vector$\mathbf {y}$that, viewed as a column vector, is equal to the$m\times 1$matrix$\mathbf {AX}.$In index notation, this amounts to:

$y_{i}=\sum _{j=1}^{n}a_{ij}x_{j}.$

One way of looking at this is that the changes from "plain" vector to column vector and back are assumed and left implicit.

Vector times matrix

Similarly, a vector$\mathbf {x}$of length$n$can be viewed as arow vector,corresponding to a$1\times n$matrix. To make it clear that a row vector is meant, it is customary in this context to represent it as thetransposeof a column vector; thus, one will see notations such as$\mathbf {x} ^{\mathrm {T} }\mathbf {A}.$The identity$\mathbf {x} ^{\mathrm {T} }\mathbf {A} =(\mathbf {A} ^{\mathrm {T} }\mathbf {x} )^{\mathrm {T} }$holds. In index notation, if$\mathbf {A}$is an$n\times p$matrix,$\mathbf {x} ^{\mathrm {T} }\mathbf {A} =\mathbf {y} ^{\mathrm {T} }$amounts to: $y_{k}=\sum _{j=1}^{n}x_{j}a_{jk}.$

Vector times vector

Thedot product$\mathbf {a} \cdot \mathbf {b}$of two vectors$\mathbf {a}$and$\mathbf {b}$of equal length is equal to the single entry of the$1\times 1$matrix resulting from multiplying these vectors as a row and a column vector, thus:$\mathbf {a} ^{\mathrm {T} }\mathbf {b}$(or$\mathbf {b} ^{\mathrm {T} }\mathbf {a},$which results in the same$1\times 1$matrix).

Illustration

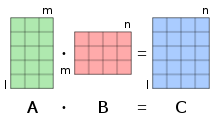
The figure to the right illustrates diagrammatically the product of two matricesAandB,showing how each intersection in the product matrix corresponds to a row ofAand a column ofB. $${\overset {4\times 2{\text{ matrix}}}{\begin{bmatrix}a_{11}&a_{12}\\\cdot &\cdot \\a_{31}&a_{32}\\\cdot &\cdot \\\end{bmatrix}}}{\overset {2\times 3{\text{ matrix}}}{\begin{bmatrix}\cdot &b_{12}&b_{13}\\\cdot &b_{22}&b_{23}\\\end{bmatrix}}}={\overset {4\times 3{\text{ matrix}}}{\begin{bmatrix}\cdot &c_{12}&\cdot \\\cdot &\cdot &\cdot \\\cdot &\cdot &c_{33}\\\cdot &\cdot &\cdot \\\end{bmatrix}}}$$

The values at the intersections, marked with circles in figure to the right, are: $${\begin{aligned}c_{12}&=a_{11}b_{12}+a_{12}b_{22}\\c_{33}&=a_{31}b_{13}+a_{32}b_{23}.\end{aligned}}$$

Fundamental applications

Historically, matrix multiplication has been introduced for facilitating and clarifying computations inlinear algebra.This strong relationship between matrix multiplication and linear algebra remains fundamental in all mathematics, as well as inphysics,chemistry,engineeringandcomputer science.

Linear maps

If avector spacehas a finitebasis,its vectors are each uniquely represented by a finitesequenceof scalars, called acoordinate vector,whose elements are thecoordinatesof the vector on the basis. These coordinate vectors form another vector space, which isisomorphicto the original vector space. A coordinate vector is commonly organized as acolumn matrix(also called acolumn vector), which is a matrix with only one column. So, a column vector represents both a coordinate vector, and a vector of the original vector space.

Alinear mapAfrom a vector space of dimensionninto a vector space of dimensionmmaps a column vector

$\mathbf {x} ={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}$

onto the column vector

$\mathbf {y} =A(\mathbf {x} )={\begin{pmatrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}\\a_{21}x_{1}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}\end{pmatrix}}.$

The linear mapAis thus defined by the matrix

$\mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},$

and maps the column vector$\mathbf {x}$to the matrix product

$\mathbf {y} =\mathbf {Ax}.$

IfBis another linear map from the preceding vector space of dimensionm,into a vector space of dimensionp,it is represented by a⁠$p\times m$⁠matrix$\mathbf {B}.$A straightforward computation shows that the matrix of thecomposite map⁠$B\circ A$⁠is the matrix product$\mathbf {BA}.$The general formula⁠$(B\circ A)(\mathbf {x} )=B(A(\mathbf {x} ))$⁠) that defines the function composition is instanced here as a specific case of associativity of matrix product (see§ Associativitybelow):

$(\mathbf {BA} )\mathbf {x} =\mathbf {B} (\mathbf {Ax} )=\mathbf {BAx}.$

Geometric rotations

See also:Rotation matrix

Using aCartesian coordinatesystem in a Euclidean plane, therotationby an angle$\ Alpha$around theoriginis a linear map. More precisely, $${\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}\cos \ Alpha &-\sin \ Alpha \\\sin \ Alpha &\cos \ Alpha \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}},$$ where the source point$(x,y)$and its image$(x',y')$are written as column vectors.

The composition of the rotation by$\ Alpha$and that by$\beta$then corresponds to the matrix product $${\begin{bmatrix}\cos \beta &-\sin \beta \\\sin \beta &\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \ Alpha &-\sin \ Alpha \\\sin \ Alpha &\cos \ Alpha \end{bmatrix}}={\begin{bmatrix}\cos \beta \cos \ Alpha -\sin \beta \sin \ Alpha &-\cos \beta \sin \ Alpha -\sin \beta \cos \ Alpha \\\sin \beta \cos \ Alpha +\cos \beta \sin \ Alpha &-\sin \beta \sin \ Alpha +\cos \beta \cos \ Alpha \end{bmatrix}}={\begin{bmatrix}\cos(\ Alpha +\beta )&-\sin(\ Alpha +\beta )\\\sin(\ Alpha +\beta )&\cos(\ Alpha +\beta )\end{bmatrix}},$$ where appropriatetrigonometric identitiesare employed for the second equality. That is, the composition corresponds to the rotation by angle$\ Alpha +\beta$,as expected.

Resource allocation in economics

The computation of the bottom left entry of$\mathbf {AB}$corresponds to the consideration of all paths (highlighted) from basic commodity$b_{4}$to final product$f_{1}$in the production flow graph.

As an example, a fictitious factory uses 4 kinds ofbasic commodities,$b_{1},b_{2},b_{3},b_{4}$to produce 3 kinds ofintermediate goods,$m_{1},m_{2},m_{3}$,which in turn are used to produce 3 kinds offinal products,$f_{1},f_{2},f_{3}$.The matrices

$\mathbf {A} ={\begin{pmatrix}1&0&1\\2&1&1\\0&1&1\\1&1&2\\\end{pmatrix}}$and$\mathbf {B} ={\begin{pmatrix}1&2&1\\2&3&1\\4&2&2\\\end{pmatrix}}$

provide the amount of basic commodities needed for a given amount of intermediate goods, and the amount of intermediate goods needed for a given amount of final products, respectively. For example, to produce one unit of intermediate good$m_{1}$,one unit of basic commodity$b_{1}$,two units of$b_{2}$,no units of$b_{3}$,and one unit of$b_{4}$are needed, corresponding to the first column of$\mathbf {A}$.

Using matrix multiplication, compute

$\mathbf {AB} ={\begin{pmatrix}5&4&3\\8&9&5\\\ 6&5&3\\11&9&6\\\end{pmatrix}};$

this matrix directly provides the amounts of basic commodities needed for given amounts of final goods. For example, the bottom left entry of$\mathbf {AB}$is computed as$1\cdot 1+1\cdot 2+2\cdot 4=11$,reflecting that$11$units of$b_{4}$are needed to produce one unit of$f_{1}$.Indeed, one$b_{4}$unit is needed for$m_{1}$,one for each of two$m_{2}$,and$2$for each of the four$m_{3}$units that go into the$f_{1}$unit, see picture.

In order to produce e.g. 100 units of the final product$f_{1}$,80 units of$f_{2}$,and 60 units of$f_{3}$,the necessary amounts of basic goods can be computed as

$(\mathbf {AB} ){\begin{pmatrix}100\\80\\60\\\end{pmatrix}}={\begin{pmatrix}1000\\1820\\1180\\2180\end{pmatrix}},$

that is,$1000$units of$b_{1}$,$1820$units of$b_{2}$,$1180$units of$b_{3}$,$2180$units of$b_{4}$are needed. Similarly, the product matrix$\mathbf {AB}$can be used to compute the needed amounts of basic goods for other final-good amount data.

System of linear equations

The general form of asystem of linear equationsis

${\begin{matrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}=b_{1},\\a_{21}x_{1}+\cdots +a_{2n}x_{n}=b_{2},\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m}.\end{matrix}}$

Using same notation as above, such a system is equivalent with the single matrixequation

$\mathbf {Ax} =\mathbf {b}.$

Dot product, bilinear form and sesquilinear form

Thedot productof two column vectors is the unique entry of the matrix product

$\mathbf {x} ^{\mathsf {T}}\mathbf {y},$

where$\mathbf {x} ^{\mathsf {T}}$is therow vectorobtained bytransposing$\mathbf {x}$.(As usual, a 1×1 matrix is identified with its unique entry.)

More generally, anybilinear formover a vector space of finite dimension may be expressed as a matrix product

$\mathbf {x} ^{\mathsf {T}}\mathbf {Ay},$

and anysesquilinear formmay be expressed as

$\mathbf {x} ^{\dagger }\mathbf {Ay},$

where$\mathbf {x} ^{\dagger }$denotes theconjugate transposeof$\mathbf {x}$(conjugate of the transpose, or equivalently transpose of the conjugate).

General properties

Matrix multiplication shares some properties with usualmultiplication.However, matrix multiplication is not defined if the number of columns of the first factor differs from the number of rows of the second factor, and it isnon-commutative,even when the product remains defined after changing the order of the factors.

Non-commutativity

An operation iscommutativeif, given two elementsAandBsuch that the product$\mathbf {A} \mathbf {B}$is defined, then$\mathbf {B} \mathbf {A}$is also defined, and$\mathbf {A} \mathbf {B} =\mathbf {B} \mathbf {A}.$

IfAandBare matrices of respective sizes⁠$m\times n$⁠and⁠$p\times q$⁠,then$\mathbf {A} \mathbf {B}$is defined if⁠$n=p$⁠,and$\mathbf {B} \mathbf {A}$is defined if⁠$m=q$⁠.Therefore, if one of the products is defined, the other one need not be defined. If⁠$m=q\neq n=p$⁠,the two products are defined, but have different sizes; thus they cannot be equal. Only if⁠$m=q=n=p$⁠,that is, ifAandBaresquare matricesof the same size, are both products defined and of the same size. Even in this case, one has in general

$\mathbf {A} \mathbf {B} \neq \mathbf {B} \mathbf {A}.$

For example

${\begin{pmatrix}0&1\\0&0\end{pmatrix}}{\begin{pmatrix}0&0\\1&0\end{pmatrix}}={\begin{pmatrix}1&0\\0&0\end{pmatrix}},$

but

${\begin{pmatrix}0&0\\1&0\end{pmatrix}}{\begin{pmatrix}0&1\\0&0\end{pmatrix}}={\begin{pmatrix}0&0\\0&1\end{pmatrix}}.$

This example may be expanded for showing that, ifAis a⁠$n\times n$⁠matrix with entries in afieldF,then$\mathbf {A} \mathbf {B} =\mathbf {B} \mathbf {A}$for every⁠$n\times n$⁠matrixBwith entries inF,if and only if$\mathbf {A} =c\,\mathbf {I}$where⁠$c\in F$⁠,andIis the⁠$n\times n$⁠identity matrix.If, instead of a field, the entries are supposed to belong to aring,then one must add the condition thatcbelongs to thecenterof the ring.

One special case where commutativity does occur is whenDandEare two (square)diagonal matrices(of the same size); thenDE=ED.Again, if the matrices are over a general ring rather than a field, the corresponding entries in each must also commute with each other for this to hold.

Distributivity

The matrix product isdistributivewith respect tomatrix addition.That is, ifA,B,C,Dare matrices of respective sizesm×n,n×p,n×p,andp×q,one has (left distributivity)

$\mathbf {A} (\mathbf {B} +\mathbf {C} )=\mathbf {AB} +\mathbf {AC},$

and (right distributivity)

$(\mathbf {B} +\mathbf {C} )\mathbf {D} =\mathbf {BD} +\mathbf {CD}.$

This results from the distributivity for coefficients by

$\sum _{k}a_{ik}(b_{kj}+c_{kj})=\sum _{k}a_{ik}b_{kj}+\sum _{k}a_{ik}c_{kj}$

$\sum _{k}(b_{ik}+c_{ik})d_{kj}=\sum _{k}b_{ik}d_{kj}+\sum _{k}c_{ik}d_{kj}.$

Product with a scalar

IfAis a matrix andca scalar, then the matrices$c\mathbf {A}$and$\mathbf {A} c$are obtained by left or right multiplying all entries ofAbyc.If the scalars have thecommutative property,then$c\mathbf {A} =\mathbf {A} c.$

If the product$\mathbf {AB}$is defined (that is, the number of columns ofAequals the number of rows ofB), then

$c(\mathbf {AB} )=(c\mathbf {A} )\mathbf {B}$and$(\mathbf {A} \mathbf {B} )c=\mathbf {A} (\mathbf {B} c).$

If the scalars have the commutative property, then all four matrices are equal. More generally, all four are equal ifcbelongs to thecenterof aringcontaining the entries of the matrices, because in this case,cX=Xcfor all matricesX.

These properties result from thebilinearityof the product of scalars:

$c\left(\sum _{k}a_{ik}b_{kj}\right)=\sum _{k}(ca_{ik})b_{kj}$

$\left(\sum _{k}a_{ik}b_{kj}\right)c=\sum _{k}a_{ik}(b_{kj}c).$

Transpose

If the scalars have thecommutative property,thetransposeof a product of matrices is the product, in the reverse order, of the transposes of the factors. That is

$(\mathbf {AB} )^{\mathsf {T}}=\mathbf {B} ^{\mathsf {T}}\mathbf {A} ^{\mathsf {T}}$

where^Tdenotes the transpose, that is the interchange of rows and columns.

This identity does not hold for noncommutative entries, since the order between the entries ofAandBis reversed, when one expands the definition of the matrix product.

Complex conjugate

IfAandBhavecomplexentries, then

$(\mathbf {AB} )^{*}=\mathbf {A} ^{*}\mathbf {B} ^{*}$

where^*denotes the entry-wisecomplex conjugateof a matrix.

This results from applying to the definition of matrix product the fact that the conjugate of a sum is the sum of the conjugates of the summands and the conjugate of a product is the product of the conjugates of the factors.

Transposition acts on the indices of the entries, while conjugation acts independently on the entries themselves. It results that, ifAandBhave complex entries, one has

$(\mathbf {AB} )^{\dagger }=\mathbf {B} ^{\dagger }\mathbf {A} ^{\dagger },$

where^†denotes theconjugate transpose(conjugate of the transpose, or equivalently transpose of the conjugate).

Associativity

Given three matricesA,BandC,the products(AB)CandA(BC)are defined if and only if the number of columns ofAequals the number of rows ofB,and the number of columns ofBequals the number of rows ofC(in particular, if one of the products is defined, then the other is also defined). In this case, one has theassociative property

$(\mathbf {AB} )\mathbf {C} =\mathbf {A} (\mathbf {BC} ).$

As for any associative operation, this allows omitting parentheses, and writing the above products as⁠$\mathbf {ABC}.$⁠

This extends naturally to the product of any number of matrices provided that the dimensions match. That is, ifA₁,A₂,...,A_nare matrices such that the number of columns ofA_iequals the number of rows ofA_{i+ 1}fori= 1,...,n– 1,then the product

$\prod _{i=1}^{n}\mathbf {A} _{i}=\mathbf {A} _{1}\mathbf {A} _{2}\cdots \mathbf {A} _{n}$

is defined and does not depend on theorder of the multiplications,if the order of the matrices is kept fixed.

These properties may be proved by straightforward but complicatedsummationmanipulations. This result also follows from the fact that matrices representlinear maps.Therefore, the associative property of matrices is simply a specific case of the associative property offunction composition.

Computational complexity depends on parenthesization

Although the result of a sequence of matrix products does not depend on theorder of operation(provided that the order of the matrices is not changed), thecomputational complexitymay depend dramatically on this order.

For example, ifA,BandCare matrices of respective sizes10×30, 30×5, 5×60,computing(AB)Cneeds10×30×5 + 10×5×60 = 4,500multiplications, while computingA(BC)needs30×5×60 + 10×30×60 = 27,000multiplications.

Algorithms have been designed for choosing the best order of products; seeMatrix chain multiplication.When the numbernof matrices increases, it has been shown that the choice of the best order has a complexity of$O(n\log n).$

Application to similarity

Anyinvertible matrix$\mathbf {P}$defines asimilarity transformation(on square matrices of the same size as$\mathbf {P}$)

$S_{\mathbf {P} }(\mathbf {A} )=\mathbf {P} ^{-1}\mathbf {A} \mathbf {P}.$

Similarity transformations map product to products, that is

$S_{\mathbf {P} }(\mathbf {AB} )=S_{\mathbf {P} }(\mathbf {A} )S_{\mathbf {P} }(\mathbf {B} ).$

In fact, one has

$\mathbf {P} ^{-1}(\mathbf {AB} )\mathbf {P} =\mathbf {P} ^{-1}\mathbf {A} (\mathbf {P} \mathbf {P} ^{-1})\mathbf {B} \mathbf {P} =(\mathbf {P} ^{-1}\mathbf {A} \mathbf {P} )(\mathbf {P} ^{-1}\mathbf {B} \mathbf {P} ).$

Square matrices

Let us denote${\mathcal {M}}_{n}(R)$the set ofn×nsquare matriceswith entries in aringR,which, in practice, is often afield.

In${\mathcal {M}}_{n}(R)$,the product is defined for every pair of matrices. This makes${\mathcal {M}}_{n}(R)$aring,which has theidentity matrixIasidentity element(the matrix whose diagonal entries are equal to 1 and all other entries are 0). This ring is also anassociativeR-algebra.

Ifn> 1,many matrices do not have amultiplicative inverse.For example, a matrix such that all entries of a row (or a column) are 0 does not have an inverse. If it exists, the inverse of a matrixAis denotedA⁻¹,and, thus verifies

$\mathbf {A} \mathbf {A} ^{-1}=\mathbf {A} ^{-1}\mathbf {A} =\mathbf {I}.$

A matrix that has an inverse is aninvertible matrix.Otherwise, it is asingular matrix.

A product of matrices is invertible if and only if each factor is invertible. In this case, one has

$(\mathbf {A} \mathbf {B} )^{-1}=\mathbf {B} ^{-1}\mathbf {A} ^{-1}.$

WhenRiscommutative,and, in particular, when it is a field, thedeterminantof a product is the product of the determinants. As determinants are scalars, and scalars commute, one has thus

$\det(\mathbf {AB} )=\det(\mathbf {BA} )=\det(\mathbf {A} )\det(\mathbf {B} ).$

The other matrixinvariantsdo not behave as well with products. Nevertheless, ifRis commutative,ABandBAhave the sametrace,the samecharacteristic polynomial,and the sameeigenvalueswith the same multiplicities. However, theeigenvectorsare generally different ifAB≠BA.

Powers of a matrix

One may raise a square matrix to anynonnegative integer powermultiplying it by itself repeatedly in the same way as for ordinary numbers. That is,

$\mathbf {A} ^{0}=\mathbf {I},$

$\mathbf {A} ^{1}=\mathbf {A},$

$\mathbf {A} ^{k}=\underbrace {\mathbf {A} \mathbf {A} \cdots \mathbf {A} } _{k{\text{ times}}}.$

Computing thekth power of a matrix needsk– 1times the time of a single matrix multiplication, if it is done with the trivial algorithm (repeated multiplication). As this may be very time consuming, one generally prefers usingexponentiation by squaring,which requires less than2 log₂kmatrix multiplications, and is therefore much more efficient.

An easy case for exponentiation is that of adiagonal matrix.Since the product of diagonal matrices amounts to simply multiplying corresponding diagonal elements together, thekth power of a diagonal matrix is obtained by raising the entries to the powerk:

${\begin{bmatrix}a_{11}&0&\cdots &0\\0&a_{22}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}\end{bmatrix}}^{k}={\begin{bmatrix}a_{11}^{k}&0&\cdots &0\\0&a_{22}^{k}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}^{k}\end{bmatrix}}.$

Abstract algebra

The definition of matrix product requires that the entries belong to a semiring, and does not require multiplication of elements of the semiring to becommutative.In many applications, the matrix elements belong to a field, although thetropical semiringis also a common choice for graphshortest pathproblems.Even in the case of matrices over fields, the product is not commutative in general, although it isassociativeand isdistributiveovermatrix addition.Theidentity matrices(which are thesquare matriceswhose entries are zero outside of the main diagonal and 1 on the main diagonal) areidentity elementsof the matrix product. It follows that then×nmatrices over aringform a ring, which is noncommutative except ifn= 1and the ground ring is commutative.

A square matrix may have amultiplicative inverse,called aninverse matrix.In the common case where the entries belong to acommutative ringR,a matrix has an inverse if and only if itsdeterminanthas a multiplicative inverse inR.The determinant of a product of square matrices is the product of the determinants of the factors. Then×nmatrices that have an inverse form agroupunder matrix multiplication, thesubgroupsof which are calledmatrix groups.Many classical groups (including allfinite groups) areisomorphicto matrix groups; this is the starting point of the theory ofgroup representations.

Matrices are themorphismsof acategory,thecategory of matrices.The objects are thenatural numbersthat measure the size of matrices, and the composition of morphisms is matrix multiplication. The source of a morphism is the number of columns of the corresponding matrix, and the target is the number of rows.

Computational complexity

Main article:Computational complexity of matrix multiplication

For implementation techniques (in particular parallel and distributed algorithms), seeMatrix multiplication algorithm.

Improvement of estimates of exponentωover time for the computational complexity of matrix multiplication$O(n^{\ Omega })$

The matrix multiplicationalgorithmthat results from the definition requires, in theworst case,⁠$n^{3}$⁠multiplications and⁠$(n-1)n^{2}$⁠additions of scalars to compute the product of two squaren×nmatrices. Itscomputational complexityis therefore⁠$O(n^{3})$⁠,in amodel of computationfor which the scalar operations take constant time.

Rather surprisingly, this complexity is not optimal, as shown in 1969 byVolker Strassen,who provided an algorithm, now calledStrassen's algorithm,with a complexity of$O(n^{\log _{2}7})\approx O(n^{2.8074}).$ Strassen's algorithm can be parallelized to further improve the performance. As of January 2024,the best peer-reviewed matrix multiplication algorithm is byVirginia Vassilevska Williams,Yinzhan Xu, Zixuan Xu, and Renfei Zhou and has complexityO(n^2.371552). It is not known whether matrix multiplication can be performed inn^{2 + o(1)}time.This would be optimal, since one must read the⁠$n^{2}$⁠elements of a matrix in order to multiply it with another matrix.

Since matrix multiplication forms the basis for many algorithms, and many operations on matrices even have the same complexity as matrix multiplication (up to a multiplicative constant), the computational complexity of matrix multiplication appears throughoutnumerical linear algebraandtheoretical computer science.

Generalizations

Other types of products of matrices include:

• Block matrix operations
• Cracovian product,defined asA∧B=B^TA
• Frobenius inner product,thedot productof matrices considered as vectors, or, equivalently the sum of the entries of the Hadamard product
• Hadamard productof two matrices of the same size, resulting in a matrix of the same size, which is the product entry-by-entry
• Kronecker productortensor product,the generalization to any size of the preceding
• Khatri-Rao productandFace-splitting product
• Outer product,also calleddyadic productortensor productof two column matrices, which is$\mathbf {a} \mathbf {b} ^{\mathsf {T}}$
• Scalar multiplication

See also

• Matrix calculus,for the interaction of matrix multiplication with operations from calculus

References

• Henry Cohn,Robert Kleinberg,Balázs Szegedy,and Chris Umans. Group-theoretic Algorithms for Matrix Multiplication.arXiv:math.GR/0511460.Proceedings of the 46th Annual Symposium on Foundations of Computer Science,23–25 October 2005, Pittsburgh, PA, IEEE Computer Society, pp. 379–388.
• Henry Cohn, Chris Umans. A Group-theoretic Approach to Fast Matrix Multiplication.arXiv:math.GR/0307321.Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science,11–14 October 2003, Cambridge, MA, IEEE Computer Society, pp. 438–449.
• Coppersmith, D.; Winograd, S. (1990)."Matrix multiplication via arithmetic progressions".J. Symbolic Comput.9(3):251–280.doi:10.1016/s0747-7171(08)80013-2.
• Horn, Roger A.; Johnson, Charles R. (1991),Topics in Matrix Analysis,Cambridge University Press,ISBN978-0-521-46713-1
• Knuth, D.E.,The Art of Computer ProgrammingVolume 2: Seminumerical Algorithms.Addison-Wesley Professional; 3 edition (November 14, 1997).ISBN978-0-201-89684-8.pp. 501.
• Press, William H.; Flannery, Brian P.;Teukolsky, Saul A.;Vetterling, William T. (2007),Numerical Recipes: The Art of Scientific Computing(3rd ed.),Cambridge University Press,ISBN978-0-521-88068-8.
• Ran Raz.On the complexity of matrix product. In Proceedings of the thirty-fourth annual ACM symposium on Theory of computing. ACM Press, 2002.doi:10.1145/509907.509932.
• Robinson, Sara,Toward an Optimal Algorithm for Matrix Multiplication,SIAM News 38(9), November 2005.PDF
• Strassen, Volker,Gaussian Elimination is not Optimal,Numer. Math. 13, p. 354–356, 1969.
• Styan, George P. H. (1973),"Hadamard Products and Multivariate Statistical Analysis"(PDF),Linear Algebra and Its Applications,6:217–240,doi:10.1016/0024-3795(73)90023-2
• Williams, Virginia Vassilevska (2012-05-19)."Multiplying matrices faster than coppersmith-winograd".Proceedings of the 44th symposium on Theory of Computing - STOC '12.ACM. pp.887–898.CiteSeerX10.1.1.297.2680.doi:10.1145/2213977.2214056.ISBN9781450312455.S2CID14350287.