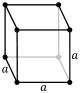
Cubic honeycomb

Cubic honeycomb

Type	Regular honeycomb
Family	Hypercube honeycomb
Inde xing^[1]	J_11,15,A₁ W₁,G₂₂
Schläfli symbol	{4,3,4}
Coxeter diagram
Cell type	{4,3}
Face type	square{4}
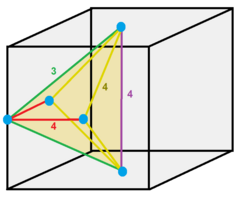
Vertex figure	octahedron
Space group Fibrifold notation	Pm3m (221) 4⁻:2
Coxeter group	${\tilde {C}}_{3}$ ,[4,3,4]
Dual	self-dual Cell:
Properties	Vertex-transitive,regular

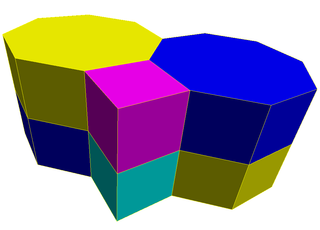
Thecubic honeycomborcubic cellulationis the only proper regular space-fillingtessellation(orhoneycomb) inEuclidean 3-spacemade up ofcubiccells. It has 4 cubes around every edge, and 8 cubes around each vertex. Itsvertex figureis a regularoctahedron.It is aself-dualtessellation withSchläfli symbol{4,3,4}.John Horton Conwaycalled this honeycomb acubille.

Ageometric honeycombis aspace-fillingofpolyhedralor higher-dimensionalcells,so that there are no gaps. It is an example of the more general mathematicaltilingortessellationin any number of dimensions.

Honeycombs are usually constructed in ordinaryEuclidean( "flat" ) space, like theconvex uniform honeycombs.They may also be constructed innon-Euclidean spaces,such ashyperbolic uniform honeycombs.Any finiteuniform polytopecan be projected to itscircumsphereto form a uniform honeycomb in spherical space.

Related honeycombs

It is part of a multidimensional family ofhypercube honeycombs,withSchläfli symbolsof the form {4,3,...,3,4}, starting with thesquare tiling,{4,4} in the plane.

It is one of 28uniform honeycombsusingconvex uniform polyhedralcells.

Isometries of simple cubic lattices

Simple cubic lattices can be distorted into lower symmetries, represented by lower crystal systems:

Crystal system	Monoclinic Triclinic	Orthorhombic	Tetragonal	Rhombohedral	Cubic
Unit cell	Parallelepiped	Rectangularcuboid	Squarecuboid	Trigonal trapezohedron	Cube
Point group Order Rotation subgroup	[ ], (*) Order 2 [ ]⁺,(1)	[2,2], (*222) Order 8 [2,2]⁺,(222)	[4,2], (*422) Order 16 [4,2]⁺,(422)	[3], (*33) Order 6 [3]⁺,(33)	[4,3], (*432) Order 48 [4,3]⁺,(432)
Diagram
Space group Rotation subgroup	Pm (6) P1 (1)	Pmmm (47) P222 (16)	P4/mmm (123) P422 (89)	R3m (160) R3 (146)	Pm3m (221) P432 (207)
Coxeter notation	-	[∞]_a×[∞]_b×[∞]_c	[4,4]_a×[∞]_c	-	[4,3,4]_a
Coxeter diagram	-			-

Uniform colorings

There is a large number ofuniform colorings,derived from different symmetries. These include:

Coxeter notation Space group	Coxeter diagram	Schläfli symbol	Colors by letters
[4,3,4] Pm3m (221)	=	{4,3,4}	1: aaaa/aaaa
[4,3^1,1] = [4,3,4,1⁺] Fm3m (225)	=	{4,3^1,1}	2: abba/baab
[4,3,4] Pm3m (221)		t_0,3{4,3,4}	4: abbc/bccd
[[4,3,4]] Pm3m (229)		t_0,3{4,3,4}	4: abbb/bbba
[4,3,4,2,∞]	or	{4,4}×t{∞}	2: aaaa/bbbb
[4,3,4,2,∞]		t₁{4,4}×{∞}	2: abba/abba
[∞,2,∞,2,∞]		t{∞}×t{∞}×{∞}	4: abcd/abcd
[∞,2,∞,2,∞] = [4,(3,4)^*]	=	t{∞}×t{∞}×t{∞}	8: abcd/efgh

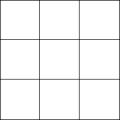
Projections

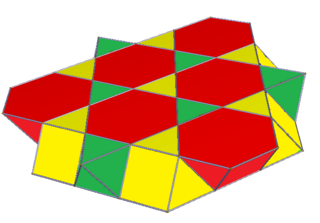
Thecubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements. The highest (hexagonal) symmetry form projects into atriangular tiling.A square symmetry projection forms asquare tiling.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

Related polytopes and honeycombs

It is related to the regular4-polytope tesseract,Schläfli symbol{4,3,3}, which exists in 4-space, and only has3cubes around each edge. It's also related to theorder-5 cubic honeycomb,Schläfli symbol {4,3,5}, ofhyperbolic spacewith 5 cubes around each edge.

It is in a sequence of polychora and honeycombs withoctahedral vertex figures.

{p,3,4} regular honeycombs
Space	S³	E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	...{∞,3,4}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

It in a sequence ofregular polytopesand honeycombs withcubic cells.

{4,3,p} regular honeycombs
Space	S³	E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	...{4,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

{p,3,p} regular honeycombs
Space	S³	Euclidean E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Related polytopes

The cubic honeycomb has a lower symmetry as a runcinated cubic honeycomb, with two sizes ofcubes.A double symmetry construction can be constructed by placing a small cube into each large cube, resulting in a nonuniform honeycomb withcubes,square prisms, and rectangular trapezoprisms (a cube withD_2dsymmetry). Its vertex figure is a triangular pyramid with its lateral faces augmented by tetrahedra.

Dual cell

The resulting honeycomb can be alternated to produce another nonuniform honeycomb with regulartetrahedra,two kinds of tetragonal disphenoids, triangular pyramids, and sphenoids. Its vertex figure hasC_3vsymmetry and has 26 triangular faces, 39 edges, and 15 vertices.

Related Euclidean tessellations

The [4,3,4],,Coxeter groupgenerates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. Theexpandedcubic honeycomb (also known as the runcinated cubic honeycomb) is geometrically identical to the cubic honeycomb.

C3 honeycombs
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁,₂,₃,₄, ₅,₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	Half	₇,₁₁,₁₂,₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		Half × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	Quarter × 2	₁₀,
Im3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

The [4,3^1,1],,Coxeter groupgenerates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.

B3 honeycombs
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Fm3m (225)	2⁻:2	[4,3^1,1] ↔ [4,3,4,1⁺]	↔	×1	₁,₂,₃,₄
Fm3m (225)	2⁻:2	<[1⁺,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	₍₁₎,₍₃₎
Pm3m (221)	4⁻:2	<[4,3^1,1]>		×2	₅,₆,₇,₍₆₎,₉,₁₀,₁₁

This honeycomb is one offive distinct uniform honeycombs^[2]constructed by the ${\tilde {A}}_{3}$ Coxeter group.The symmetry can be multiplied by the symmetry of rings in theCoxeter–Dynkin diagrams:

A3 honeycombs
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde {A}}_{3}$	(None)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ×2₁ ↔ ${\tilde {B}}_{3}$	₁,₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] or [2⁺[3^[4]]]	↔	${\tilde {A}}_{3}$ ×2₂	₃
Pm3m (221)	4⁻:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ×4₁ ↔ ${\tilde {C}}_{3}$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ×8 ↔ ½ ${\tilde {C}}_{3}$ ×2	_(*)
Im3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ×8 ↔ ${\tilde {C}}_{3}$ ×2	₅

Rectified cubic honeycomb

Rectified cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	r{4,3,4} or t₁{4,3,4} r{4,3^1,1} 2r{4,3^1,1} r{3^[4]}
Coxeter diagrams	= = ===
Cells	r{4,3} {3,4}
Faces	triangle{3} square{4}
Vertex figure	square prism
Space group Fibrifold notation	Pm3m (221) 4⁻:2
Coxeter group	${\tilde {C}}_{3}$ ,[4,3,4]
Dual	oblate octahedrille Cell: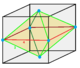
Properties	Vertex-transitive,edge-transitive

Therectified cubic honeycomborrectified cubic cellulationis a uniform space-fillingtessellation(orhoneycomb) in Euclidean 3-space. It is composed ofoctahedraandcuboctahedrain a ratio of 1:1, with asquare prism vertex figure.

John Horton Conwaycalls this honeycomb acuboctahedrille,and its dual anoblate octahedrille.

Projections

Therectified cubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

Symmetry

There are fouruniform coloringsfor the cells of this honeycomb with reflective symmetry, listed by theirCoxeter group,andWythoff constructionname, and theCoxeter diagrambelow.

Symmetry	[4,3,4] ${\tilde {C}}_{3}$	[1⁺,4,3,4] [4,3^1,1], ${\tilde {B}}_{3}$	[4,3,4,1⁺] [4,3^1,1], ${\tilde {B}}_{3}$	[1⁺,4,3,4,1⁺] [3^[4]], ${\tilde {A}}_{3}$
Space group	Pm3m (221)	Fm3m (225)	Fm3m (225)	F43m (216)
Coloring
Coxeter diagram
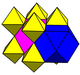
Coxeter diagram
Vertex figure
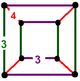
Vertex figure symmetry	D_4h [4,2] (*224) order 16	D_2h [2,2] (*222) order 8	C_4v [4] (*44) order 8	C_2v [2] (*22) order 4

This honeycomb can be divided ontrihexagonal tilingplanes, using thehexagoncenters of the cuboctahedra, creating twotriangular cupolae.Thisscaliform honeycombis represented by Coxeter diagram,and symbol s₃{2,6,3}, withcoxeter notationsymmetry [2⁺,6,3].

.

Related polytopes

A double symmetry construction can be made by placing octahedra on the cuboctahedra, resulting in a nonuniform honeycomb with two kinds ofoctahedra(regular octahedra and triangular antiprisms). The vertex figure is asquare bifrustum.The dual is composed ofelongated square bipyramids.

Dual cell

Truncated cubic honeycomb

Truncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t{4,3,4} or t_0,1{4,3,4} t{4,3^1,1}
Coxeter diagrams	=
Cell type	t{4,3} {3,4}
Face type	triangle{3} octagon{8}
Vertex figure	isoscelessquare pyramid
Space group Fibrifold notation	Pm3m (221) 4⁻:2
Coxeter group	${\tilde {C}}_{3}$ ,[4,3,4]
Dual	Pyramidille Cell: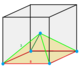
Properties	Vertex-transitive

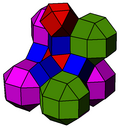
Thetruncated cubic honeycombortruncated cubic cellulationis a uniform space-fillingtessellation(orhoneycomb) in Euclidean 3-space. It is composed oftruncated cubesandoctahedrain a ratio of 1:1, with an isoscelessquare pyramid vertex figure.

John Horton Conwaycalls this honeycomb atruncated cubille,and its dualpyramidille.

Projections

Thetruncated cubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

Symmetry

There is a seconduniform coloringby reflectional symmetry of theCoxeter groups,the second seen with alternately colored truncated cubic cells.

Construction	Bicantellated alternate cubic	Truncated cubic honeycomb
Coxeter group	[4,3^1,1], ${\tilde {B}}_{3}$	[4,3,4], ${\tilde {C}}_{3}$ =<[4,3^1,1]>
Space group	Fm3m	Pm3m
Coloring
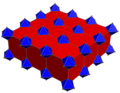
Coxeter diagram	=
Vertex figure

Related polytopes

A double symmetry construction can be made by placing octahedra on the truncated cubes, resulting in a nonuniform honeycomb with two kinds ofoctahedra(regular octahedra and triangular antiprisms) and two kinds oftetrahedra(tetragonal disphenoids and digonal disphenoids). The vertex figure is an octakis square cupola.

Vertex figure

Dual cell

Bitruncated cubic honeycomb

Bitruncated cubic honeycomb

Type	Uniform honeycomb
Schläfli symbol	2t{4,3,4} t_1,2{4,3,4}
Coxeter-Dynkin diagram
Cells	t{3,4}
Faces	square{4} hexagon{6}
Edge figure	isosceles triangle{3}
Vertex figure	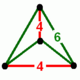tetragonal disphenoid
Symmetry group Fibrifold notation Coxeter notation	Im3m (229) 8^o:2 [[4,3,4]]
Coxeter group	${\tilde {C}}_{3}$ ,[4,3,4]
Dual	Oblate tetrahedrille Disphenoid tetrahedral honeycomb Cell:
Properties	Vertex-transitive,edge-transitive,cell-transitive

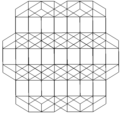
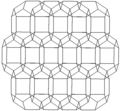
Thebitruncated cubic honeycombis a space-fillingtessellation(orhoneycomb) inEuclidean 3-spacemade up oftruncated octahedra(or, equivalently,bitruncatedcubes). It has fourtruncated octahedraaround each vertex, in atetragonal disphenoid vertex figure.Being composed entirely oftruncated octahedra,it iscell-transitive.It is alsoedge-transitive,with 2 hexagons and one square on each edge, andvertex-transitive.It is one of 28uniform honeycombs.

John Horton Conwaycalls this honeycomb atruncated octahedrillein hisArchitectonic and catoptric tessellationlist, with its dual called anoblate tetrahedrille,also called adisphenoid tetrahedral honeycomb.Although a regulartetrahedroncan not tessellate space alone, this dual has identicaldisphenoid tetrahedroncells withisosceles trianglefaces.

Projections

Thebitruncated cubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements. The highest (hexagonal) symmetry form projects into a nonuniformrhombitrihexagonal tiling.A square symmetry projection forms two overlappingtruncated square tiling,which combine together as achamfered square tiling.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
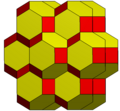
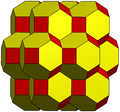
Solid
Frame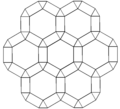

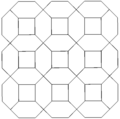
Symmetry

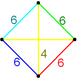
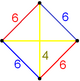
The vertex figure for this honeycomb is adisphenoid tetrahedron,and it is also theGoursat tetrahedron(fundamental domain) for the ${\tilde {A}}_{3}$ Coxeter group.This honeycomb has four uniform constructions, with the truncated octahedral cells having differentCoxeter groupsandWythoff constructions.These uniform symmetries can be represented by coloring differently the cells in each construction.

Five uniform colorings by cell
Space group	Im3m (229)	Pm3m (221)	Fm3m (225)	F43m (216)	Fd3m (227)
Fibrifold	8^o:2	4⁻:2	2⁻:2	1^o:2	2⁺:2
Coxeter group	${\tilde {C}}_{3}$ ×2 [[4,3,4]] =[4[3^[4]]] =	${\tilde {C}}_{3}$ [4,3,4] =[2[3^[4]]] =	${\tilde {B}}_{3}$ [4,3^1,1] =<[3^[4]]> =	${\tilde {A}}_{3}$ [3^[4]]	${\tilde {A}}_{3}$ ×2 [[3^[4]]] =[[3^[4]]]
Coxeter diagram
truncated octahedra	1	1:1 :	2:1:1 ::	1:1:1:1 :::	1:1 :
Vertex figure
Vertex figure symmetry	[2⁺,4] (order 8)	[2] (order 4)	[ ] (order 2)	[ ]⁺ (order 1)	[2]⁺ (order 2)
Image Colored by cell

Related polytopes

Nonuniform variants with [4,3,4] symmetry and two types of truncated octahedra can be doubled by placing the two types of truncated octahedra to produce a nonuniform honeycomb withtruncated octahedraandhexagonal prisms(as ditrigonal trapezoprisms). Its vertex figure is aC_2v-symmetrictriangular bipyramid.

This honeycomb can then be alternated to produce another nonuniform honeycomb withpyritohedral icosahedra,octahedra(as triangular antiprisms), andtetrahedra(as sphenoids). Its vertex figure hasC_2vsymmetry and consists of 2pentagons,4rectangles,4isosceles triangles(divided into two sets of 2), and 4scalene triangles.

Alternated bitruncated cubic honeycomb

Alternated bitruncated cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	2s{4,3,4} 2s{4,3^1,1} sr{3^[4]}
Coxeter diagrams	= = =
Cells	{3,3} s{3,3}
Faces	triangle{3}
Vertex figure
Coxeter group	[[4,3⁺,4]], ${\tilde {C}}_{3}$
Dual	Ten-of-diamonds honeycomb Cell:
Properties	Vertex-transitive,non-uniform

Thealternated bitruncated cubic honeycomborbisnub cubic honeycombis non-uniform, with the highest symmetry construction reflecting an alternation of the uniform bitruncated cubic honeycomb. A lower-symmetry construction involves regular icosahedra paired with golden icosahedra (with 8 equilateral triangles paired with 12 golden triangles). There are three constructions from three relatedCoxeter diagrams:,,and.These have symmetry [4,3⁺,4], [4,(3^1,1)⁺] and [3^[4]]⁺respectively. The first and last symmetry can be doubled as [[4,3⁺,4]] and [[3^[4]]]⁺.

This honeycomb is represented in the boron atoms of theα-rhombohedral crystal.The centers of the icosahedra are located at the fcc positions of the lattice.^[3]

Five uniform colorings
Space group	I3(204)	Pm3(200)	Fm3(202)	Fd3(203)	F23 (196)
Fibrifold	8^−o	4⁻	2⁻	2^o+	1^o
Coxeter group	[[4,3⁺,4]]	[4,3⁺,4]	[4,(3^1,1)⁺]	[[3^[4]]]⁺	[3^[4]]⁺
Coxeter diagram
Order	double	full	half	quarter double	quarter

Cantellated cubic honeycomb

Cantellated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	rr{4,3,4} or t_0,2{4,3,4} rr{4,3^1,1}
Coxeter diagram	=
Cells	rr{4,3} r{4,3} {}x{4}
Vertex figure	wedge
Space group Fibrifold notation	Pm3m (221) 4⁻:2
Coxeter group	[4,3,4], ${\tilde {C}}_{3}$
Dual	quarter oblate octahedrille Cell: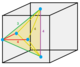
Properties	Vertex-transitive

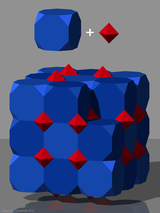
Thecantellated cubic honeycomborcantellated cubic cellulationis a uniform space-fillingtessellation(orhoneycomb) in Euclidean 3-space. It is composed ofrhombicuboctahedra,cuboctahedra,andcubesin a ratio of 1:1:3, with awedge vertex figure.

John Horton Conwaycalls this honeycomb a2-RCO-trille,and its dualquarter oblate octahedrille.

Images

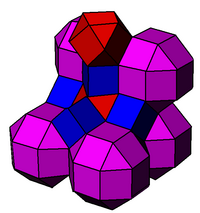
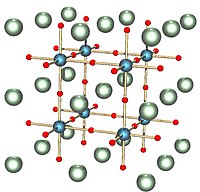	It is closely related to theperovskite structure,shown here with cubic symmetry, with atoms placed at the center of the cells of this honeycomb.

Projections

Thecantellated cubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

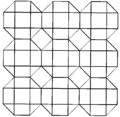
Symmetry

There is a seconduniform coloringsby reflectional symmetry of theCoxeter groups,the second seen with alternately colored rhombicuboctahedral cells.

Vertex uniform colorings by cell
Construction	Truncated cubic honeycomb	Bicantellated alternate cubic
Coxeter group	[4,3,4], ${\tilde {C}}_{3}$ =<[4,3^1,1]>	[4,3^1,1], ${\tilde {B}}_{3}$
Space group	Pm3m	Fm3m
Coxeter diagram
Coloring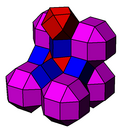
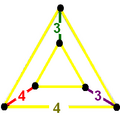
Vertex figure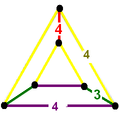
Vertex figure symmetry	[ ] order 2	[ ]⁺ order 1

Related polytopes

A double symmetry construction can be made by placing cuboctahedra on the rhombicuboctahedra, which results in therectified cubic honeycomb,by taking the triangular antiprism gaps as regularoctahedra,square antiprism pairs and zero-height tetragonal disphenoids as components of thecuboctahedron.Other variants result incuboctahedra,square antiprisms,octahedra(as triangular antipodiums), andtetrahedra(as tetragonal disphenoids), with a vertex figure topologically equivalent to acubewith atriangular prismattached to one of its square faces.

Quarter oblate octahedrille

The dual of thecantellated cubic honeycombis called aquarter oblate octahedrille,acatoptric tessellationwithCoxeter diagram,containing faces from two of four hyperplanes of the cubic [4,3,4] fundamental domain.

It has irregular triangle bipyramid cells which can be seen as 1/12 of a cube, made from the cube center, 2 face centers, and 2 vertices.

Cantitruncated cubic honeycomb

Cantitruncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	tr{4,3,4} or t_0,1,2{4,3,4} tr{4,3^1,1}
Coxeter diagram	=
Cells	tr{4,3} t{3,4} {}x{4}
Faces	square{4} hexagon{6} octagon{8}
Vertex figure	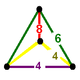mirrored sphenoid
Coxeter group	[4,3,4], ${\tilde {C}}_{3}$
Symmetry group Fibrifold notation	Pm3m (221) 4⁻:2
Dual	triangular pyramidille Cells:
Properties	Vertex-transitive

Thecantitruncated cubic honeycomborcantitruncated cubic cellulationis a uniform space-fillingtessellation(orhoneycomb) in Euclidean 3-space, made up oftruncated cuboctahedra,truncated octahedra,andcubesin a ratio of 1:1:3, with amirrored sphenoid vertex figure.

John Horton Conwaycalls this honeycomb an-tCO-trille,and its dualtriangular pyramidille.

Images

Four cells exist around each vertex:

Projections

Thecantitruncated cubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

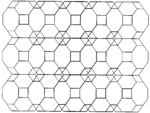
Symmetry

Cells can be shown in two different symmetries. The linearCoxeter diagramform can be drawn with one color for each cell type. The bifurcating diagram form can be drawn with two types (colors) oftruncated cuboctahedroncells alternating.

Construction	Cantitruncated cubic	Omnitruncated alternate cubic
Coxeter group	[4,3,4], ${\tilde {C}}_{3}$ =<[4,3^1,1]>	[4,3^1,1], ${\tilde {B}}_{3}$
Space group	Pm3m (221)	Fm3m (225)
Fibrifold	4⁻:2	2⁻:2
Coloring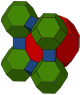
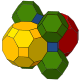
Coxeter diagram
Vertex figure
Vertex figure symmetry	[ ] order 2	[ ]⁺ order 1

Triangular pyramidille

The dual of thecantitruncated cubic honeycombis called atriangular pyramidille,withCoxeter diagram,.This honeycomb cells represents the fundamental domains of ${\tilde {B}}_{3}$ symmetry.

A cell can be as 1/24 of a translational cube with vertices positioned: taking two corner, ne face center, and the cube center. The edge colors and labels specify how many cells exist around the edge.

Related polyhedra and honeycombs

It is related to askew apeirohedronwithvertex configuration4.4.6.6, with the octagons and some of the squares removed. It can be seen as constructed by augmenting truncated cuboctahedral cells, or by augmenting alternated truncated octahedra and cubes.

Two views

Related polytopes

A double symmetry construction can be made by placing truncated octahedra on the truncated cuboctahedra, resulting in a nonuniform honeycomb withtruncated octahedra,hexagonal prisms(as ditrigonal trapezoprisms),cubes(as square prisms),triangular prisms(asC_2v-symmetric wedges), andtetrahedra(as tetragonal disphenoids). Its vertex figure is topologically equivalent to theoctahedron.

Vertex figure

Dual cell

Alternated cantitruncated cubic honeycomb

Alternated cantitruncated cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	sr{4,3,4} sr{4,3^1,1}
Coxeter diagrams	=
Cells	s{4,3} s{3,3} {3,3}
Faces	triangle{3} square{4}
Vertex figure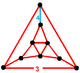
Coxeter group	[(4,3)⁺,4]
Dual	Cell:
Properties	Vertex-transitive,non-uniform

Thealternated cantitruncated cubic honeycomborsnub rectified cubic honeycombcontains three types of cells:snub cubes,icosahedra(withT_hsymmetry),tetrahedra(as tetragonal disphenoids), and new tetrahedral cells created at the gaps.
Although it is not uniform, constructionally it can be given asCoxeter diagramsor.

Despite being non-uniform, there is a near-miss version with two edge lengths shown below, one of which is around 4.3% greater than the other. The snub cubes in this case are uniform, but the rest of the cells are not.

Cantic snub cubic honeycomb

Orthosnub cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	2s₀{4,3,4}
Coxeter diagrams
Cells	s₂{3,4} s{3,3} {}x{3}
Faces	triangle{3} square{4}
Vertex figure
Coxeter group	[4⁺,3,4]
Dual	Cell:
Properties	Vertex-transitive,non-uniform

Thecantic snub cubic honeycombis constructed by snubbing thetruncated octahedrain a way that leaves onlyrectanglesfrom thecubes(square prisms). It is not uniform but it can be represented asCoxeter diagram.It hasrhombicuboctahedra(withT_hsymmetry),icosahedra(withT_hsymmetry), andtriangular prisms(asC_2v-symmetry wedges) filling the gaps.^[4]

Related polytopes

A double symmetry construction can be made by placing icosahedra on the rhombicuboctahedra, resulting in a nonuniform honeycomb withicosahedra,octahedra(as triangular antiprisms),triangular prisms(asC_2v-symmetric wedges), andsquare pyramids.

Vertex figure

Dual cell

Runcitruncated cubic honeycomb

Runcitruncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t_0,1,3{4,3,4}
Coxeter diagrams
Cells	rr{4,3} t{4,3} {}x{8} {}x{4}
Faces	triangle{3} square{4} octagon{8}
Vertex figure	isosceles-trapezoidal pyramid
Coxeter group	[4,3,4], ${\tilde {C}}_{3}$
Space group Fibrifold notation	Pm3m (221) 4⁻:2
Dual	square quarter pyramidille Cell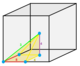
Properties	Vertex-transitive

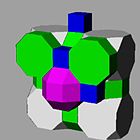
Theruncitruncated cubic honeycomborruncitruncated cubic cellulationis a uniformspace-filling tessellation(orhoneycomb) in Euclidean 3-space. It is composed ofrhombicuboctahedra,truncated cubes,octagonal prisms,andcubesin a ratio of 1:1:3:3, with anisosceles-trapezoidal pyramid vertex figure.

Its name is derived from itsCoxeter diagram,with three ringed nodes representing 3 active mirrors in theWythoff constructionfrom its relation to theregularcubic honeycomb.

John Horton Conwaycalls this honeycomb a1-RCO-trille,and its dualsquare quarter pyramidille.

Projections

Theruncitruncated cubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid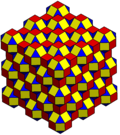
Frame

Related skew apeirohedron

Two related uniformskew apeirohedronsexists with the samevertex arrangement,seen as boundary cells from a subset of cells. One has triangles and squares, and the other triangles, squares, and octagons.

Square quarter pyramidille

The dual to theruncitruncated cubic honeycombis called asquare quarter pyramidille,withCoxeter diagram.Faces exist in 3 of 4 hyperplanes of the [4,3,4], ${\tilde {C}}_{3}$ Coxeter group.

Cells are irregular pyramids and can be seen as 1/24 of a cube, using one corner, one mid-edge point, two face centers, and the cube center.

Related polytopes

A double symmetry construction can be made by placing rhombicuboctahedra on the truncated cubes, resulting in a nonuniform honeycomb withrhombicuboctahedra,octahedra(as triangular antiprisms),cubes(as square prisms), two kinds oftriangular prisms(bothC_2v-symmetric wedges), andtetrahedra(as digonal disphenoids). Its vertex figure is topologically equivalent to theaugmented triangular prism.

Vertex figure

Dual cell

Omnitruncated cubic honeycomb

Omnitruncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t_0,1,2,3{4,3,4}
Coxeter diagram
Cells	tr{4,3} {}x{8}
Faces	square{4} hexagon{6} octagon{8}
Vertex figure	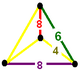phyllic disphenoid
Symmetry group Fibrifold notation Coxeter notation	Im3m (229) 8^o:2 [[4,3,4]]
Coxeter group	[4,3,4], ${\tilde {C}}_{3}$
Dual	eighth pyramidille Cell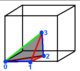
Properties	Vertex-transitive

Theomnitruncated cubic honeycomboromnitruncated cubic cellulationis a uniform space-fillingtessellation(orhoneycomb) in Euclidean 3-space. It is composed oftruncated cuboctahedraandoctagonal prismsin a ratio of 1:3, with aphyllic disphenoid vertex figure.

John Horton Conwaycalls this honeycomb ab-tCO-trille,and its dualeighth pyramidille.

Projections

Theomnitruncated cubic honeycombcan be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections
Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame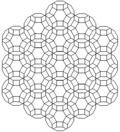

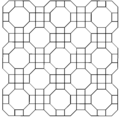
Symmetry

Cells can be shown in two different symmetries. TheCoxeter diagramform has two colors oftruncated cuboctahedraandoctagonal prisms.The symmetry can be doubled by relating the first and last branches of the Coxeter diagram, which can be shown with one color for all the truncated cuboctahedral and octagonal prism cells.

Two uniform colorings
Symmetry	${\tilde {C}}_{3}$ ,[4,3,4]	${\tilde {C}}_{3}$ ×2, [[4,3,4]]
Space group	Pm3m (221)	Im3m (229)
Fibrifold	4⁻:2	8^o:2
Coloring
Coxeter diagram
Vertex figure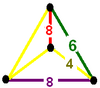

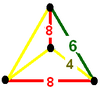
Related polyhedra

Two related uniformskew apeirohedronexist with the samevertex arrangement.The first has octagons removed, and vertex configuration 4.4.4.6. It can be seen as truncated cuboctahedra and octagonal prisms augmented together. The second can be seen as augmented octagonal prisms, vertex configuration 4.8.4.8.

4.4.4.6	4.8.4.8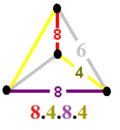

Related polytopes

Nonuniform variants with [4,3,4] symmetry and two types of truncated cuboctahedra can be doubled by placing the two types of truncated cuboctahedra on each other to produce a nonuniform honeycomb withtruncated cuboctahedra,octagonal prisms,hexagonal prisms(as ditrigonal trapezoprisms), and two kinds ofcubes(as rectangular trapezoprisms and theirC_2v-symmetric variants). Its vertex figure is an irregulartriangular bipyramid.

Vertex figure

Dual cell

This honeycomb can then be alternated to produce another nonuniform honeycomb withsnub cubes,square antiprisms,octahedra(as triangular antiprisms), and three kinds oftetrahedra(as tetragonal disphenoids, phyllic disphenoids, and irregular tetrahedra).

Vertex figure

Alternated omnitruncated cubic honeycomb

Alternated omnitruncated cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	ht_0,1,2,3{4,3,4}
Coxeter diagram
Cells	s{4,3} s{2,4} {3,3}
Faces	triangle{3} square{4}
Vertex figure
Symmetry	[[4,3,4]]⁺
Dual	Dual alternated omnitruncated cubic honeycomb
Properties	Vertex-transitive,non-uniform

Analternated omnitruncated cubic honeycomboromnisnub cubic honeycombcan be constructed byalternationof the omnitruncated cubic honeycomb, although it can not be made uniform, but it can be givenCoxeter diagram:and has symmetry [[4,3,4]]⁺.It makessnub cubesfrom thetruncated cuboctahedra,square antiprismsfrom theoctagonal prisms,and creates newtetrahedralcells from the gaps.

Dual alternated omnitruncated cubic honeycomb

Dual alternated omnitruncated cubic honeycomb
Type	Dual alternated uniform honeycomb
Schläfli symbol	dht_0,1,2,3{4,3,4}
Coxeter diagram
Cell
Vertex figures	pentagonal icositetrahedron tetragonal trapezohedron tetrahedron
Symmetry	[[4,3,4]]⁺
Dual	Alternated omnitruncated cubic honeycomb
Properties	Cell-transitive

Adual alternated omnitruncated cubic honeycombis a space-filling honeycomb constructed as the dual of thealternated omnitruncated cubic honeycomb.

24 cells fit around a vertex, making a chiraloctahedral symmetrythat can be stacked in all 3-dimensions:

Individual cells have 2-fold rotational symmetry. In 2D orthogonal projection, this looks like a mirror symmetry.

Cell views
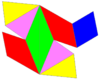Net

Runcic cantitruncated cubic honeycomb

Runcic cantitruncated cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	sr₃{4,3,4}
Coxeter diagrams
Cells	s₂{3,4} s{4,3} {}x{4} {}x{3}
Faces	triangle{3} square{4}
Vertex figure
Coxeter group	[4,3⁺,4]
Dual	Cell: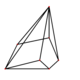
Properties	Vertex-transitive,non-uniform

Theruncic cantitruncated cubic honeycomborruncic cantitruncated cubic cellulationis constructed by removing alternating long rectangles from the octagons and is not uniform, but it can be represented asCoxeter diagram.It hasrhombicuboctahedra(withT_hsymmetry),snub cubes,two kinds ofcubes:square prisms and rectangular trapezoprisms (topologically equivalent to acubebut withD_2dsymmetry), andtriangular prisms(asC_2v-symmetry wedges) filling the gaps.

Biorthosnub cubic honeycomb

Biorthosnub cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	2s_0,3{4,3,4}
Coxeter diagrams
Cells	s₂{3,4} {}x{4}
Faces	triangle{3} square{4}
Vertex figure	(Tetragonal antiwedge)
Coxeter group	[[4,3⁺,4]]
Dual	Cell:
Properties	Vertex-transitive,non-uniform

Thebiorthosnub cubic honeycombis constructed by removing alternating long rectangles from the octagons orthogonally and is not uniform, but it can be represented asCoxeter diagram.It hasrhombicuboctahedra(withT_hsymmetry) and two kinds ofcubes:square prisms and rectangular trapezoprisms (topologically equivalent to acubebut withD_2dsymmetry).

Truncated square prismatic honeycomb

Truncated square prismatic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t{4,4}×{∞} or t_0,1,3{4,4,2,∞} tr{4,4}×{∞} or t_0,1,2,3{4,4,∞}
Coxeter-Dynkin diagram
Cells	{}x{8} {}x{4}
Faces	square{4} octagon{8}
Coxeter group	[4,4,2,∞]
Dual	Tetrakis square prismatic tiling Cell:
Properties	Vertex-transitive

Thetruncated square prismatic honeycombortomo-square prismatic cellulationis a space-fillingtessellation(orhoneycomb) inEuclidean 3-space.It is composed ofoctagonal prismsandcubesin a ratio of 1:1.

It is constructed from atruncated square tilingextruded into prisms.

It is one of 28convex uniform honeycombs.

Snub square prismatic honeycomb

Snub square prismatic honeycomb
Type	Uniform honeycomb
Schläfli symbol	s{4,4}×{∞} sr{4,4}×{∞}
Coxeter-Dynkin diagram
Cells	{}x{4} {}x{3}
Faces	triangle{3} square{4}
Coxeter group	[4⁺,4,2,∞] [(4,4)⁺,2,∞]
Dual	Cairo pentagonal prismatic honeycomb Cell:
Properties	Vertex-transitive

Thesnub square prismatic honeycomborsimo-square prismatic cellulationis a space-fillingtessellation(orhoneycomb) inEuclidean 3-space.It is composed ofcubesandtriangular prismsin a ratio of 1:2.

It is constructed from asnub square tilingextruded into prisms.

It is one of 28convex uniform honeycombs.

Snub square antiprismatic honeycomb

Snub square antiprismatic honeycomb
Type	Convex honeycomb
Schläfli symbol	ht_1,2,3{4,4,2,∞} ht_0,1,2,3{4,4,∞}
Coxeter-Dynkin diagram
Cells	s{2,4} {3,3}
Faces	triangle{3} square{4}
Vertex figure
Symmetry	[4,4,2,∞]⁺
Properties	Vertex-transitive,non-uniform

Asnub square antiprismatic honeycombcan be constructed byalternationof the truncated square prismatic honeycomb, although it can not be made uniform, but it can be givenCoxeter diagram:and has symmetry [4,4,2,∞]⁺.It makessquare antiprismsfrom theoctagonal prisms,tetrahedra(as tetragonal disphenoids) from thecubes,and two tetrahedra from thetriangular bipyramids.

References

^For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).
^[1],A0000296-1 cases, skipping one with zero marks
^Williams, 1979, p 199, Figure 5-38.
^cantic snub cubic honeycomb

John H. Conway,Heidi Burgiel,Chaim Goodman-Strauss,(2008)The Symmetries of Things,ISBN 978-1-56881-220-5(Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
Coxeter, H.S.M.Regular Polytopes,(3rd edition, 1973), Dover edition,ISBN 0-486-61480-8p. 296, Table II: Regular honeycombs
George Olshevsky,Uniform Panoploid Tetracombs,Manuscript (2006)(Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
Branko Grünbaum,Uniform tilings of 3-space.Geombinatorics4(1994), 49 - 56.
Kaleidoscopes: Selected Writings of H.S.M. Coxeter,edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,ISBN978-0-471-01003-6[2]
- (Paper 22) H.S.M. Coxeter,Regular and Semi Regular Polytopes I,[Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
A. Andreini,Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative(On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
Klitzing, Richard."3D Euclidean Honeycombs x4o3o4o - chon - O1".
Uniform Honeycombs in 3-Space: 01-Chon

v t e Fundamental convexregularanduniform honeycombsin dimensions 2–9
Space	Family	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
E²	Uniform tiling	0_[3]	δ₃	hδ₃	qδ₃	Hexagonal
E³	Uniform convex honeycomb	0_[4]	δ₄	hδ₄	qδ₄
E⁴	Uniform 4-honeycomb	0_[5]	δ₅	hδ₅	qδ₅	24-cell honeycomb
E⁵	Uniform 5-honeycomb	0_[6]	δ₆	hδ₆	qδ₆
E⁶	Uniform 6-honeycomb	0_[7]	δ₇	hδ₇	qδ₇	2₂₂
E⁷	Uniform 7-honeycomb	0_[8]	δ₈	hδ₈	qδ₈	1₃₃•3₃₁
E⁸	Uniform 8-honeycomb	0_[9]	δ₉	hδ₉	qδ₉	1₅₂•2₅₁•5₂₁
E⁹	Uniform 9-honeycomb	0_[10]	δ₁₀	hδ₁₀	qδ₁₀
E¹⁰	Uniform 10-honeycomb	0_[11]	δ₁₁	hδ₁₁	qδ₁₁
E^n-1	Uniform (n-1)-honeycomb	0_[n]	δ_n	hδ_n	qδ_n	1_k2•2_k1•k₂₁

[1] For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).

[2] [1],A0000296-1 cases, skipping one with zero marks

[3] Williams, 1979, p 199, Figure 5-38.

[4] tic snub cubic honeycomb

[1]

[2]

[3]

[4]

Cubic honeycomb

Related honeycombs

Isometries of simple cubic lattices

Uniform colorings

Projections

Related polytopes and honeycombs

Related polytopes

Related Euclidean tessellations

Rectified cubic honeycomb

Projections

Symmetry

Related polytopes

Truncated cubic honeycomb

Projections

Symmetry

Related polytopes

Bitruncated cubic honeycomb

Projections

Symmetry

Related polytopes

Alternated bitruncated cubic honeycomb

Cantellated cubic honeycomb

Images

Projections

Symmetry

Related polytopes

Quarter oblate octahedrille

Cantitruncated cubic honeycomb

Images

Projections

Symmetry

Triangular pyramidille

Related polyhedra and honeycombs

Related polytopes

Alternated cantitruncated cubic honeycomb

Cantic snub cubic honeycomb

Related polytopes

Runcitruncated cubic honeycomb

Projections

Related skew apeirohedron

Square quarter pyramidille

Related polytopes

Omnitruncated cubic honeycomb

Projections

Symmetry

Related polyhedra

Related polytopes

Alternated omnitruncated cubic honeycomb

Dual alternated omnitruncated cubic honeycomb

Runcic cantitruncated cubic honeycomb

Biorthosnub cubic honeycomb

Truncated square prismatic honeycomb

Snub square prismatic honeycomb

Snub square antiprismatic honeycomb

See also

References