Triangular number

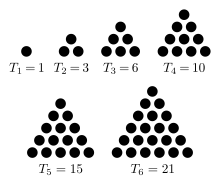
Atriangular numberortriangle numbercounts objects arranged in anequilateral triangle.Triangular numbers are a type offigurate number,other examples beingsquare numbersandcube numbers.Thenth triangular number is the number of dots in the triangular arrangement withndots on each side, and is equal to the sum of thennatural numbersfrom 1 ton.Thesequenceof triangular numbers, starting with the0th triangular number,is

The first six triangular numbers (not starting withT₀)

Triangular Numbers Plot

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666...

(sequenceA000217in theOEIS)

Formula

Derivation of triangular numbers from a left-justifiedPascal's triangle.

Natural numbers

Triangular numbers

Tetrahedral numbers

Pentatope numbers

5-simplexnumbers

6-simplexnumbers

7-simplexnumbers

The triangular numbers are given by the following explicit formulas:

$\displaystyle {\begin{aligned}T_{n}&=\sum _{k=1}^{n}k=1+2+\dotsb +n\\&={\frac {n^{2}+n{\vphantom {(n+1)}}}{2}}={\frac {n(n+1)}{2}}\\&={n+1 \choose 2}\end{aligned}}$

where$\textstyle {n+1 \choose 2}$is notation for abinomial coefficient.It represents the number of distinct pairs that can be selected fromn+ 1objects, and it is read aloud as "nplus one choose two ".

The fact that the$n$th triangular number equals$n(n+1)/2$can be illustrated using avisual proof.For every triangular number$T_{n}$,imagine a "half-rectangle" arrangement of objects corresponding to the triangular number, as in the figure below. Copying this arrangement and rotating it to create a rectangular figure doubles the number of objects, producing a rectangle with dimensions$n\times (n+1)$,which is also the number of objects in the rectangle. Clearly, the triangular number itself is always exactly half of the number of objects in such a figure, or:$T_{n}={\frac {n(n+1)}{2}}$.The example$T_{4}$follows:

$2T_{4}=4(4+1)=20$(green plus yellow) implies that$T_{4}={\frac {4(4+1)}{2}}=10$(green).

This formula can be proven formally usingmathematical induction.It is clearly true for$1$:

$$T_{1}=\sum _{k=1}^{1}k={\frac {1(1+1)}{2}}={\frac {2}{2}}=1.$$

Now assume that, for some natural number$m$,$T_{m}=\sum _{k=1}^{m}k={\frac {m(m+1)}{2}}$.Adding$m+1$to this yields

$${\begin{aligned}\sum _{k=1}^{m}k+(m+1)&={\frac {m(m+1)}{2}}+m+1\\&={\frac {m(m+1)+2m+2}{2}}\\&={\frac {m^{2}+m+2m+2}{2}}\\&={\frac {m^{2}+3m+2}{2}}\\&={\frac {(m+1)(m+2)}{2}},\end{aligned}}$$

so if the formula is true for$m$,it is true for$m+1$.Since it is clearly true for$1$,it is therefore true for$2$,$3$,and ultimately all natural numbers$n$by induction.

The German mathematician and scientist,Carl Friedrich Gauss,is said to have found this relationship in his early youth, by multiplying⁠n/2⁠pairs of numbers in the sum by the values of each pairn+ 1.However, regardless of the truth of this story, Gauss was not the first to discover this formula, and some find it likely that its origin goes back to thePythagoreansin the 5th century BC.The two formulas were described by the Irish monkDicuilin about 816 in hisComputus.An English translation of Dicuil's account is available.

Proof without wordsthat the number of possible handshakes between n people is the (n−1)th triangular number

The triangular numberT_nsolves thehandshake problemof counting the number of handshakes if each person in a room withn+ 1people shakes hands once with each person. In other words, the solution to the handshake problem ofnpeople isT_n−1.The functionTis the additive analog of thefactorialfunction, which is theproductsof integers from 1 ton.

This same function was coined as the "Termial function"byDonald Knuth'sThe Art of Computer Programmingand denotedn?(analog for the factorial notationn!)

For example,10 termialis equivalent to:

$$10?=1+2+3+4+5+6+7+8+9+10=55$$

which of course, corresponds to thetenth triangular number.

The number of line segments between closest pairs of dots in the triangle can be represented in terms of the number of dots or with arecurrence relation: $$L_{n}=3T_{n-1}=3{n \choose 2};~~~L_{n}=L_{n-1}+3(n-1),~L_{1}=0.$$

In thelimit,the ratio between the two numbers, dots and line segments is $$\lim _{n\to \infty }{\frac {T_{n}}{L_{n}}}={\frac {1}{3}}.$$

Relations to other figurate numbers

Triangular numbers have a wide variety of relations to other figurate numbers.

Most simply, the sum of two consecutive triangular numbers is a square number, since:

$T_{n-1}+T_{n}$

$={\frac {1}{2}}\,n(n-1)+{\frac {1}{2}}\,n(n+1)$

$={\frac {1}{2}}\,n{\Bigl (}(n-1)+(n+1){\Bigr )}$

$=n^{2}$

with the sum being the square of the difference between the two (and thus the difference of the two being the square root of the sum): $$T_{n}+T_{n-1}=\left({\frac {n^{2}}{2}}+{\frac {n}{2}}\right)+\left({\frac {\left(n-1\right)^{2}}{2}}+{\frac {n-1{\vphantom {\left(n-1\right)^{2}}}}{2}}\right)=\left({\frac {n^{2}}{2}}+{\frac {n}{2}}\right)+\left({\frac {n^{2}}{2}}-{\frac {n}{2}}\right)=n^{2}=(T_{n}-T_{n-1})^{2}.$$

This property, colloquially known as the theorem ofTheon of Smyrna,is visually demonstrated in the following sum, which represents$T_{4}+T_{5}=5^{2}$asdigit sums:

${\begin{array}{ccccccc}&4&3&2&1&\\+&1&2&3&4&5\\\hline &5&5&5&5&5\end{array}}$

This fact can also be demonstrated graphically by positioning the triangles in opposite directions to create a square:

6 + 10 = 1610 + 15 = 25

The double of a triangular number, as in the visual proof from the above section§ Formula,is called apronic number.

There are infinitely many triangular numbers that are also square numbers; e.g., 1, 36, 1225. Some of them can be generated by a simple recursive formula: $$S_{n+1}=4S_{n}\left(8S_{n}+1\right)$$with$S_{1}=1.$

Allsquare triangular numbersare found from the recursion $$S_{n}=34S_{n-1}-S_{n-2}+2$$with$S_{0}=0$and$S_{1}=1.$

A square whose side length is a triangular number can be partitioned into squares and half-squares whose areas add to cubes. This shows that the square of thenth triangular number is equal to the sum of the firstncube numbers.

Also, thesquare of thenth triangular numberis the same as the sum of the cubes of the integers 1 ton.This can also be expressed as $$\sum _{k=1}^{n}k^{3}=\left(\sum _{k=1}^{n}k\right)^{2}.$$

The sum of the firstntriangular numbers is thenthtetrahedral number: $$\sum _{k=1}^{n}T_{k}=\sum _{k=1}^{n}{\frac {k(k+1)}{2}}={\frac {n(n+1)(n+2)}{6}}.$$

More generally, the difference between thenthm-gonal numberand thenth(m+ 1)-gonal number is the(n− 1)th triangular number. For example, the sixthheptagonal number(81) minus the sixthhexagonal number(66) equals the fifth triangular number, 15. Every other triangular number is a hexagonal number. Knowing the triangular numbers, one can reckon anycentered polygonal number;thenth centeredk-gonal number is obtained by the formula $$Ck_{n}=kT_{n-1}+1$$

whereTis a triangular number.

The positive difference of two triangular numbers is atrapezoidal number.

The pattern found for triangular numbers$\sum _{n_{1}=1}^{n_{2}}n_{1}={\binom {n_{2}+1}{2}}$and for tetrahedral numbers$\sum _{n_{2}=1}^{n_{3}}\sum _{n_{1}=1}^{n_{2}}n_{1}={\binom {n_{3}+2}{3}},$which usesbinomial coefficients,can be generalized. This leads to the formula: $$\sum _{n_{k-1}=1}^{n_{k}}\sum _{n_{k-2}=1}^{n_{k-1}}\dots \sum _{n_{2}=1}^{n_{3}}\sum _{n_{1}=1}^{n_{2}}n_{1}={\binom {n_{k}+k-1}{k}}$$

The fourth triangular number equals the third tetrahedral number as thenthk-simplex number equals thekthn-simplex number due to the symmetry ofPascal's triangle,and its diagonals being simplex numbers; similarly, the fifth triangular number (15) equals the thirdpentatope number,and so forth

Other properties

Triangular numbers correspond to the first-degree case ofFaulhaber's formula.

{{{annotations}}}

Proof without wordsthat all hexagonal numbers are odd-sided triangular numbers

Alternating triangular numbers (1, 6, 15, 28,...) are also hexagonal numbers.

Every evenperfect numberis triangular (as well as hexagonal), given by the formula $$M_{p}2^{p-1}={\frac {M_{p}(M_{p}+1)}{2}}=T_{M_{p}}$$ whereM_pis aMersenne prime.No odd perfect numbers are known; hence, all known perfect numbers are triangular.

For example, the third triangular number is (3 × 2 =) 6, the seventh is (7 × 4 =) 28, the 31st is (31 × 16 =) 496, and the 127th is (127 × 64 =) 8128.

The final digit of a triangular number is 0, 1, 3, 5, 6, or 8, and thus such numbers never end in 2, 4, 7, or 9. A final 3 must be preceded by a 0 or 5; a final 8 must be preceded by a 2 or 7.

Inbase 10,thedigital rootof a nonzero triangular number is always 1, 3, 6, or 9. Hence, every triangular number is either divisible by three or has a remainder of 1 when divided by 9:

0 = 9 × 0

1 = 9 × 0 + 1

3 = 9 × 0 + 3

6 = 9 × 0 + 6

10 = 9 × 1 + 1

15 = 9 × 1 + 6

21 = 9 × 2 + 3

28 = 9 × 3 + 1

36 = 9 × 4

45 = 9 × 5

55 = 9 × 6 + 1

66 = 9 × 7 + 3

78 = 9 × 8 + 6

91 = 9 × 10 + 1

...

The digital root pattern for triangular numbers, repeating every nine terms, as shown above, is "1, 3, 6, 1, 6, 3, 1, 9, 9".

The converse of the statement above is, however, not always true. For example, the digital root of 12, which is not a triangular number, is 3 and divisible by three.

Ifxis a triangular number, thenax+bis also a triangular number, givenais an odd square andb=⁠a− 1/8⁠.Note that bwill always be a triangular number, because8T_n+ 1 = (2n+ 1)²,which yields all the odd squares are revealed by multiplying a triangular number by 8 and adding 1, and the process forbgivenais an odd square is the inverse of this operation. The first several pairs of this form (not counting1x+ 0) are:9x+ 1,25x+ 3,49x+ 6,81x+ 10,121x+ 15,169x+ 21,... etc. Givenxis equal toT_n,these formulas yieldT_{3n+ 1},T_{5n+ 2},T_{7n+ 3},T_{9n+ 4},and so on.

The sum of thereciprocalsof all the nonzero triangular numbers is $$\sum _{n=1}^{\infty }{1 \over {{n^{2}+n} \over 2}}=2\sum _{n=1}^{\infty }{1 \over {n^{2}+n}}=2.$$

This can be shown by using the basic sum of atelescoping series: $$\sum _{n=1}^{\infty }{1 \over {n(n+1)}}=1.$$

Two other formulas regarding triangular numbers are $$T_{a+b}=T_{a}+T_{b}+ab$$ and $$T_{ab}=T_{a}T_{b}+T_{a-1}T_{b-1},$$ both of which can easily be established either by looking at dot patterns (see above) or with some simple algebra.

In 1796, Gauss discovered that every positive integer is representable as a sum of three triangular numbers (possibly includingT₀= 0), writing in his diary his famous words, "ΕΥΡΗΚΑ!num = Δ + Δ + Δ".This theorem does not imply that the triangular numbers are different (as in the case of 20 = 10 + 10 + 0), nor that a solution with exactly three nonzero triangular numbers must exist. This is a special case of theFermat polygonal number theorem.

The largest triangular number of the form2^k− 1is4095(seeRamanujan–Nagell equation).

Wacław Franciszek Sierpińskiposed the question as to the existence of four distinct triangular numbers ingeometric progression.It was conjectured by Polish mathematicianKazimierz Szymiczekto be impossible and was later proven by Fang and Chen in 2007.

Formulas involving expressing an integer as the sum of triangular numbers are connected totheta functions,in particular theRamanujan theta function.

Applications

The maximum number of pieces,pobtainable withnstraight cuts is then-th triangular number plus one, forming the lazy caterer's sequence (OEIS A000124)

Afully connected networkofncomputing devices requires the presence ofT_n− 1cables or other connections; this is equivalent to the handshake problem mentioned above.

In a tournament format that uses a round-robingroup stage,the number of matches that need to be played betweennteams is equal to the triangular numberT_n− 1.For example, a group stage with 4 teams requires 6 matches, and a group stage with 8 teams requires 28 matches. This is also equivalent to the handshake problem and fully connected network problems.

One way of calculating thedepreciationof an asset is thesum-of-years' digits method,which involves findingT_n,wherenis the length in years of the asset's useful life. Each year, the item loses(b−s) ×⁠n−y/T_n⁠,wherebis the item's beginning value (in units of currency),sis its final salvage value,nis the total number of years the item is usable, andythe current year in the depreciation schedule. Under this method, an item with a usable life ofn= 4 years would lose⁠4/10⁠of its "losable" value in the first year,⁠3/10⁠in the second,⁠2/10⁠in the third, and⁠1/10⁠in the fourth, accumulating a total depreciation of⁠10/10⁠(the whole) of the losable value.

Board gamedesigners Geoffrey Engelstein and Isaac Shalev describe triangular numbers as having achieved "nearly the status of a mantra or koan amonggame designers",describing them as" deeply intuitive "and" featured in an enormous number of games, [proving] incredibly versatile at providing escalating rewards for larger sets without overly incentivizing specialization to the exclusion of all other strategies ".

Relationship between the maximum number of pips on an end of adominoand the number of dominoes in its set
(values in bold are common)

Max. pips	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
Tn	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	161	190	210	231	253

Triangular roots and tests for triangular numbers

By analogy with thesquare rootofx,one can define the (positive) triangular root ofxas the numbernsuch thatT_n=x: $$n={\frac {{\sqrt {8x+1}}-1}{2}}$$

which follows immediately from thequadratic formula.So an integerxis triangularif and only if8x+ 1is a square. Equivalently, if the positive triangular rootnofxis an integer, thenxis thenth triangular number.

Alternative name

As stated, an alternative name proposed byDonald Knuth,by analogy tofactorials,is "termial", with the notationn?for thenth triangular number.However, although some other sources use this name and notation,they are not in wide use.

See also

• 1 + 2 + 3 + 4 + ⋯
• Doubly triangular number,a triangular number whose position in the sequence of triangular numbers is also a triangular number
• Tetractys,an arrangement of ten points in a triangle, important in Pythagoreanism

External links

• "Arithmetic series",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Triangular numbersatcut-the-knot
• There exist triangular numbers that are also squareatcut-the-knot
• Weisstein, Eric W."Triangular Number".MathWorld.
• Hypertetrahedral Polytopic Rootsby Rob Hubbard, including the generalisation totriangular cube roots,some higher dimensions, and some approximate formulas