Bijection

| Function |
|---|
| x↦f (x) |
| History of the function concept |
| Types bydomainandcodomain |
| Classes/properties |
| Constructions |
| Generalizations |
| List of specific functions |
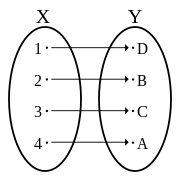
Abijection,bijective function,orone-to-one correspondencebetween two mathematicalsetsis afunctionsuch that each element of the first set (the domain) is mapped to exactly one element of the second set (the codomain). Equivalently, a bijection is arelationbetween two sets such that each element of either set is paired with exactly one element of the other set.
A function is bijectiveif and only ifit isinvertible;that is, a functionis bijective if and only if there is a functiontheinverseoff,such that each of the two ways forcomposingthe two functions produces anidentity function:for eachinandfor eachin
For example, themultiplication by twodefines a bijection from theintegersto theeven numbers,which has thedivision by twoas its inverse function.
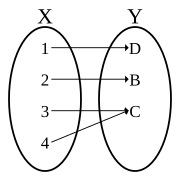
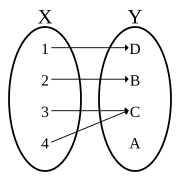
A function is bijective if and only if it is bothinjective(orone-to-one)—meaning that each element in the codomain is mapped to from at most one element of the domain—andsurjective(oronto)—meaning that each element of the codomain is mapped to from at least one element of the domain. The termone-to-one correspondencemust not be confused withone-to-one function,which means injective but not necessarily surjective.
The elementary operation ofcountingestablishes a bijection from somefinite setto the firstnatural numbers(1, 2, 3,...),up to the number of elements in the counted set. It results that two finite sets have the same number of elements if and only if there exists a bijection between them. More generally, two sets are said to have the samecardinal numberif there exists a bijection between them.
A bijective function from a set to itself is also called apermutation,[1]and the set of all permutations of a set forms itssymmetric group.
Some bijections with further properties have received specific names, which includeautomorphisms,isomorphisms,homeomorphisms,diffeomorphisms,permutation groups,and mostgeometric transformations.Galois correspondencesare bijections between sets ofmathematical objectsof apparently very different nature.
Definition
[edit]For abinary relationpairing elements of setXwith elements of setYto be a bijection, four properties must hold:
- each element ofXmust be paired with at least one element ofY,
- no element ofXmay be paired with more than one element ofY,
- each element ofYmust be paired with at least one element ofX,and
- no element ofYmay be paired with more than one element ofX.
Satisfying properties (1) and (2) means that a pairing is afunctionwithdomainX.It is more common to see properties (1) and (2) written as a single statement: Every element ofXis paired with exactly one element ofY.Functions which satisfy property (3) are said to be "ontoY"and are calledsurjections(orsurjective functions). Functions which satisfy property (4) are said to be "one-to-one functions"and are calledinjections(orinjective functions).[2]With this terminology, a bijection is a function which is both a surjection and an injection, or using other words, a bijection is a function which is both "one-to-one" and "onto".[3]
Examples
[edit]Batting line-up of a baseball or cricket team
[edit]Consider thebatting line-upof a baseball orcricketteam (or any list of all the players of any sports team where every player holds a specific spot in a line-up). The setXwill be the players on the team (of size nine in the case of baseball) and the setYwill be the positions in the batting order (1st, 2nd, 3rd, etc.) The "pairing" is given by which player is in what position in this order. Property (1) is satisfied since each player is somewhere in the list. Property (2) is satisfied since no player bats in two (or more) positions in the order. Property (3) says that for each position in the order, there is some player batting in that position and property (4) states that two or more players are never batting in the same position in the list.
Seats and students of a classroom
[edit]In a classroom there are a certain number of seats. A bunch of students enter the room and the instructor asks them to be seated. After a quick look around the room, the instructor declares that there is a bijection between the set of students and the set of seats, where each student is paired with the seat they are sitting in. What the instructor observed in order to reach this conclusion was that:
- Every student was in a seat (there was no one standing),
- No student was in more than one seat,
- Every seat had someone sitting there (there were no empty seats), and
- No seat had more than one student in it.
The instructor was able to conclude that there were just as many seats as there were students, without having to count either set.
More mathematical examples
[edit]
- For any setX,theidentity function1X:X→X,1X(x) =xis bijective.
- The functionf:R→R,f(x) = 2x+ 1 is bijective, since for eachythere is a uniquex= (y− 1)/2 such thatf(x) =y.More generally, anylinear functionover the reals,f:R→R,f(x) =ax+b(whereais non-zero) is a bijection. Each real numberyis obtained from (or paired with) the real numberx= (y−b)/a.
- The functionf:R→ (−π/2, π/2), given byf(x) = arctan(x) is bijective, since each real numberxis paired with exactly one angleyin the interval (−π/2, π/2) so that tan(y) =x(that is,y= arctan(x)). If thecodomain(−π/2, π/2) was made larger to include an integer multiple of π/2, then this function would no longer be onto (surjective), since there is no real number which could be paired with the multiple of π/2 by this arctan function.
- Theexponential function,g:R→R,g(x) = ex,is not bijective: for instance, there is noxinRsuch thatg(x) = −1, showing thatgis not onto (surjective). However, if the codomain is restricted to the positive real numbers,thengwould be bijective; its inverse (see below) is thenatural logarithmfunction ln.
- The functionh:R→R+,h(x) =x2is not bijective: for instance,h(−1) =h(1) = 1, showing thathis not one-to-one (injective). However, if thedomainis restricted to,thenhwould be bijective; its inverse is the positive square root function.
- BySchröder–Bernstein theorem,given any two setsXandY,and two injective functionsf:X → Yandg:Y → X,there exists a bijective functionh:X → Y.
Inverses
[edit]A bijectionfwith domainX(indicated byf:X → Yinfunctional notation) also defines aconverse relationstarting inYand going toX(by turning the arrows around). The process of "turning the arrows around" for an arbitrary function does not,in general,yield a function, but properties (3) and (4) of a bijection say that this inverse relation is a function with domainY.Moreover, properties (1) and (2) then say that this inversefunctionis a surjection and an injection, that is, theinverse functionexists and is also a bijection. Functions that have inverse functions are said to beinvertible.A function is invertible if and only if it is a bijection.
Stated in concise mathematical notation, a functionf:X → Yis bijective if and only if it satisfies the condition
- for everyyinYthere is a uniquexinXwithy=f(x).
Continuing with the baseball batting line-up example, the function that is being defined takes as input the name of one of the players and outputs the position of that player in the batting order. Since this function is a bijection, it has an inverse function which takes as input a position in the batting order and outputs the player who will be batting in that position.
Composition
[edit]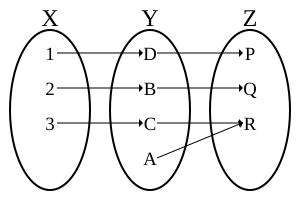
Thecompositionof two bijectionsf:X → Yandg:Y → Zis a bijection, whose inverse is given byis.
Conversely, if the compositionof two functions is bijective, it only follows thatfisinjectiveandgissurjective.
Cardinality
[edit]IfXandYarefinite sets,then there exists a bijection between the two setsXandYif and only ifXandYhave the same number of elements. Indeed, inaxiomatic set theory,this is taken as the definition of "same number of elements" (equinumerosity), and generalising this definition toinfinite setsleads to the concept ofcardinal number,a way to distinguish the various sizes of infinite sets.
Properties
[edit]- A functionf:R→Ris bijective if and only if itsgraphmeets every horizontal and vertical line exactly once.
- IfXis a set, then the bijective functions fromXto itself, together with the operation of functional composition (∘), form agroup,thesymmetric groupofX,which is denoted variously by S(X),SX,orX!(Xfactorial).
- Bijections preservecardinalitiesof sets: for a subsetAof the domain with cardinality |A| and subsetBof the codomain with cardinality |B|, one has the following equalities:
- |f(A)| = |A| and |f−1(B)| = |B|.
- IfXandYarefinite setswith the same cardinality, andf:X → Y,then the following are equivalent:
- fis a bijection.
- fis asurjection.
- fis aninjection.
- For a finite setS,there is a bijection between the set of possibletotal orderingsof the elements and the set of bijections fromStoS.That is to say, the number ofpermutationsof elements ofSis the same as the number of total orderings of that set—namely,n!.
Category theory
[edit]Bijections are precisely theisomorphismsin thecategorySetofsetsand set functions. However, the bijections are not always the isomorphisms for more complex categories. For example, in the categoryGrpofgroups,the morphisms must behomomorphismssince they must preserve the group structure, so the isomorphisms aregroup isomorphismswhich are bijective homomorphisms.
Generalization to partial functions
[edit]The notion of one-to-one correspondence generalizes topartial functions,where they are calledpartial bijections,although partial bijections are only required to be injective. The reason for this relaxation is that a (proper) partial function is already undefined for a portion of its domain; thus there is no compelling reason to constrain its inverse to be atotal function,i.e. defined everywhere on its domain. The set of all partial bijections on a given base set is called thesymmetric inverse semigroup.[4]
Another way of defining the same notion is to say that a partial bijection fromAtoBis any relation R(which turns out to be a partial function) with the property thatRis thegraph ofa bijectionf:A′→B′,whereA′is asubsetofAandB′is a subset ofB.[5]
When the partial bijection is on the same set, it is sometimes called aone-to-one partialtransformation.[6]An example is theMöbius transformationsimply defined on the complex plane, rather than its completion to the extended complex plane.[7]
Gallery
[edit]See also
[edit]- Ax–Grothendieck theorem
- Bijection, injection and surjection
- Bijective numeration
- Bijective proof
- Category theory
- Multivalued function
Notes
[edit]- ^Hall 1959,p. 3
- ^There are names associated to properties (1) and (2) as well. A relation which satisfies property (1) is called atotal relationand a relation satisfying (2) is asingle valued relation.
- ^"Bijection, Injection, And Surjection | Brilliant Math & Science Wiki".brilliant.org.Retrieved7 December2019.
- ^Christopher Hollings (16 July 2014).Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups.American Mathematical Society. p. 251.ISBN978-1-4704-1493-1.
- ^Francis Borceux (1994).Handbook of Categorical Algebra: Volume 2, Categories and Structures.Cambridge University Press. p. 289.ISBN978-0-521-44179-7.
- ^Pierre A. Grillet (1995).Semigroups: An Introduction to the Structure Theory.CRC Press. p. 228.ISBN978-0-8247-9662-4.
- ^John Meakin (2007). "Groups and semigroups: connections and contrasts". In C.M. Campbell; M.R. Quick; E.F. Robertson; G.C. Smith (eds.).Groups St Andrews 2005 Volume 2.Cambridge University Press. p. 367.ISBN978-0-521-69470-4.preprintcitingLawson, M. V. (1998)."The Möbius Inverse Monoid".Journal of Algebra.200(2): 428–438.doi:10.1006/jabr.1997.7242.
References
[edit]This topic is a basic concept in set theory and can be found in any text which includes an introduction to set theory. Almost all texts that deal with an introduction to writing proofs will include a section on set theory, so the topic may be found in any of these:
- Hall, Marshall Jr.(1959).The Theory of Groups.MacMillan.
- Wolf (1998).Proof, Logic and Conjecture: A Mathematician's Toolbox.Freeman.
- Sundstrom (2003).Mathematical Reasoning: Writing and Proof.Prentice-Hall.
- Smith; Eggen; St.Andre (2006).A Transition to Advanced Mathematics (6th Ed.).Thomson (Brooks/Cole).
- Schumacher (1996).Chapter Zero: Fundamental Notions of Abstract Mathematics.Addison-Wesley.
- O'Leary (2003).The Structure of Proof: With Logic and Set Theory.Prentice-Hall.
- Morash.Bridge to Abstract Mathematics.Random House.
- Maddox (2002).Mathematical Thinking and Writing.Harcourt/ Academic Press.
- Lay (2001).Analysis with an introduction to proof.Prentice Hall.
- Gilbert; Vanstone (2005).An Introduction to Mathematical Thinking.Pearson Prentice-Hall.
- Fletcher; Patty.Foundations of Higher Mathematics.PWS-Kent.
- Iglewicz; Stoyle.An Introduction to Mathematical Reasoning.MacMillan.
- Devlin, Keith (2004).Sets, Functions, and Logic: An Introduction to Abstract Mathematics.Chapman & Hall/ CRC Press.
- D'Angelo; West (2000).Mathematical Thinking: Problem Solving and Proofs.Prentice Hall.
- Cupillari(1989).The Nuts and Bolts of Proofs.Wadsworth.ISBN9780534103200.
- Bond.Introduction to Abstract Mathematics.Brooks/Cole.
- Barnier; Feldman (2000).Introduction to Advanced Mathematics.Prentice Hall.
- Ash.A Primer of Abstract Mathematics.MAA.