Jump to content

Combinatorics

From Wikipedia, the free encyclopedia
(Redirected fromCombinatorial)
Not to be confused withCombinatoriality.
"Combinatorial" redirects here. For combinatorial logic in computer science, seeCombinatorial logic.
Part of a series on
Mathematics
Areas
Relationship with sciences
Mathematics Portal

Combinatoricsis an area ofmathematicsprimarily concerned withcounting,both as a means and as an end to obtaining results, and certain properties offinitestructures.It is closely related to many other areas of mathematics and has many applications ranging fromlogictostatistical physicsand fromevolutionary biologytocomputer science.

Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas ofpure mathematics,notably inalgebra,probability theory,topology,andgeometry,[1]as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving anad hocsolution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right.[2]One of the oldest and most accessible parts of combinatorics isgraph theory,which by itself has numerous natural connections to other areas. Combinatorics is used frequently in computer science to obtain formulas and estimates in theanalysis of algorithms.

Definition

[edit]

The full scope of combinatorics is not universally agreed upon.[3]According toH.J. Ryser,a definition of the subject is difficult because it crosses so many mathematical subdivisions.[4]Insofar as an area can be described by the types of problems it addresses, combinatorics is involved with:

  • theenumeration(counting) of specified structures, sometimes referred to as arrangements or configurations in a very general sense, associated with finite systems,
  • theexistenceof such structures that satisfy certain given criteria,
  • theconstructionof these structures, perhaps in many ways, and
  • optimization:finding the "best" structure or solution among several possibilities, be it the "largest", "smallest" or satisfying some otheroptimality criterion.

Leon Mirskyhas said: "combinatorics is a range of linked studies which have something in common and yet diverge widely in their objectives, their methods, and the degree of coherence they have attained."[5]One way to define combinatorics is, perhaps, to describe its subdivisions with their problems and techniques. This is the approach that is used below. However, there are also purely historical reasons for including or not including some topics under the combinatorics umbrella.[6]Although primarily concerned with finite systems, some combinatorial questions and techniques can be extended to an infinite (specifically,countable) butdiscretesetting.

History

[edit]
An example ofchange ringing(with six bells), one of the earliest nontrivial results ingraph theory.
Main article:History of combinatorics

Basic combinatorial concepts and enumerative results appeared throughout theancient world.IndianphysicianSushrutaasserts inSushruta Samhitathat 63 combinations can be made out of 6 different tastes, taken one at a time, two at a time, etc., thus computing all 26− 1 possibilities.GreekhistorianPlutarchdiscusses an argument betweenChrysippus(3rd century BCE) andHipparchus(2nd century BCE) of a rather delicate enumerative problem, which was later shown to be related toSchröder–Hipparchus numbers.[7][8][9]Earlier, in theOstomachion,Archimedes(3rd century BCE) may have considered the number of configurations of atiling puzzle,[10]while combinatorial interests possibly were present in lost works byApollonius.[11][12]

In theMiddle Ages,combinatorics continued to be studied, largely outside of theEuropean civilization.TheIndianmathematicianMahāvīra(c. 850) provided formulae for the number ofpermutationsandcombinations,[13][14]and these formulas may have been familiar to Indian mathematicians as early as the 6th century CE.[15]ThephilosopherandastronomerRabbiAbraham ibn Ezra(c. 1140) established the symmetry ofbinomial coefficients,while a closed formula was obtained later by thetalmudistandmathematicianLevi ben Gerson(better known as Gersonides), in 1321.[16] The arithmetical triangle—a graphical diagram showing relationships among the binomial coefficients—was presented by mathematicians in treatises dating as far back as the 10th century, and would eventually become known asPascal's triangle.Later, inMedieval England,campanologyprovided examples of what is now known asHamiltonian cyclesin certainCayley graphson permutations.[17][18]

During theRenaissance,together with the rest of mathematics and thesciences,combinatorics enjoyed a rebirth. Works ofPascal,Newton,Jacob BernoulliandEulerbecame foundational in the emerging field. In modern times, the works ofJ.J. Sylvester(late 19th century) andPercy MacMahon(early 20th century) helped lay the foundation forenumerativeandalgebraic combinatorics.Graph theoryalso enjoyed an increase of interest at the same time, especially in connection with thefour color problem.

In the second half of the 20th century, combinatorics enjoyed a rapid growth, which led to establishment of dozens of new journals and conferences in the subject.[19]In part, the growth was spurred by new connections and applications to other fields, ranging from algebra to probability, fromfunctional analysistonumber theory,etc. These connections shed the boundaries between combinatorics and parts of mathematics and theoretical computer science, but at the same time led to a partial fragmentation of the field.

Approaches and subfields of combinatorics

[edit]

Enumerative combinatorics

[edit]
Fivebinary treeson threevertices,an example ofCatalan numbers.
Main article:Enumerative combinatorics

Enumerative combinatorics is the most classical area of combinatorics and concentrates on counting the number of certain combinatorial objects. Although counting the number of elements in a set is a rather broadmathematical problem,many of the problems that arise in applications have a relatively simple combinatorial description.Fibonacci numbersis the basic example of a problem in enumerative combinatorics. Thetwelvefold wayprovides a unified framework for countingpermutations,combinationsandpartitions.

Analytic combinatorics

[edit]
Main article:Analytic combinatorics

Analytic combinatoricsconcerns the enumeration of combinatorial structures using tools fromcomplex analysisandprobability theory.In contrast with enumerative combinatorics, which uses explicit combinatorial formulae andgenerating functionsto describe the results, analytic combinatorics aims at obtainingasymptotic formulae.

Partition theory

[edit]
Aplane partition.
Main article:Partition theory

Partition theory studies various enumeration and asymptotic problems related tointeger partitions,and is closely related toq-series,special functionsandorthogonal polynomials.Originally a part ofnumber theoryandanalysis,it is now considered a part of combinatorics or an independent field. It incorporates thebijective approachand various tools in analysis andanalytic number theoryand has connections withstatistical mechanics.Partitions can be graphically visualized withYoung diagramsorFerrers diagrams.They occur in a number of branches ofmathematicsandphysics,including the study ofsymmetric polynomialsand of thesymmetric groupand ingroup representation theoryin general.

Graph theory

[edit]
Petersen graph.
Main article:Graph theory

Graphs are fundamental objects in combinatorics. Considerations of graph theory range from enumeration (e.g., the number of graphs onnvertices withkedges) to existing structures (e.g., Hamiltonian cycles) to algebraic representations (e.g., given a graphGand two numbersxandy,does theTutte polynomialTG(x,y) have a combinatorial interpretation?). Although there are very strong connections between graph theory and combinatorics, they are sometimes thought of as separate subjects.[20]While combinatorial methods apply to many graph theory problems, the two disciplines are generally used to seek solutions to different types of problems.

Design theory

[edit]
Main article:Combinatorial design

Design theory is a study ofcombinatorial designs,which are collections of subsets with certainintersectionproperties.Block designsare combinatorial designs of a special type. This area is one of the oldest parts of combinatorics, such as inKirkman's schoolgirl problemproposed in 1850. The solution of the problem is a special case of aSteiner system,which play an important role in theclassification of finite simple groups.The area has further connections tocoding theoryand geometric combinatorics.

Combinatorial design theory can be applied to the area ofdesign of experiments.Some of the basic theory of combinatorial designs originated in the statisticianRonald Fisher's work on the design of biological experiments. Modern applications are also found in a wide gamut of areas includingfinite geometry,tournament scheduling,lotteries,mathematical chemistry,mathematical biology,algorithm design and analysis,networking,group testingandcryptography.[21]

Finite geometry

[edit]
Main article:Finite geometry

Finite geometry is the study ofgeometric systemshaving only a finite number of points. Structures analogous to those found in continuous geometries (Euclidean plane,real projective space,etc.) but defined combinatorially are the main items studied. This area provides a rich source of examples fordesign theory.It should not be confused with discrete geometry (combinatorial geometry).

Order theory

[edit]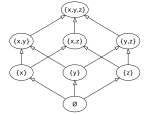
Hasse diagramof thepowersetof {x,y,z} ordered byinclusion.
Main article:Order theory

Order theory is the study ofpartially ordered sets,both finite and infinite. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". Various examples of partial orders appear inalgebra,geometry, number theory and throughout combinatorics and graph theory. Notable classes and examples of partial orders includelatticesandBoolean algebras.

Matroid theory

[edit]
Main article:Matroid theory

Matroid theory abstracts part ofgeometry.It studies the properties of sets (usually, finite sets) of vectors in avector spacethat do not depend on the particular coefficients in alinear dependencerelation. Not only the structure but also enumerative properties belong to matroid theory. Matroid theory was introduced byHassler Whitneyand studied as a part of order theory. It is now an independent field of study with a number of connections with other parts of combinatorics.

Extremal combinatorics

[edit]
Main article:Extremal combinatorics

Extremal combinatorics studies how large or how small a collection of finite objects (numbers,graphs,vectors,sets,etc.) can be, if it has to satisfy certain restrictions. Much of extremal combinatorics concernsclassesofset systems;this is called extremal set theory. For instance, in ann-element set, what is the largest number ofk-elementsubsetsthat can pairwise intersect one another? What is the largest number of subsets of which none contains any other? The latter question is answered bySperner's theorem,which gave rise to much of extremal set theory.

The types of questions addressed in this case are about the largest possible graph which satisfies certain properties. For example, the largesttriangle-free graphon2nvertices is acomplete bipartite graphKn,n.Often it is too hard even to find the extremal answerf(n) exactly and one can only give anasymptotic estimate.

Ramsey theoryis another part of extremal combinatorics. It states that anysufficiently largeconfiguration will contain some sort of order. It is an advanced generalization of thepigeonhole principle.

Probabilistic combinatorics

[edit]
Self-avoiding walkin asquare grid graph.
Main article:Probabilistic method

In probabilistic combinatorics, the questions are of the following type: what is the probability of a certain property for a random discrete object, such as arandom graph?For instance, what is the average number of triangles in a random graph? Probabilistic methods are also used to determine the existence of combinatorial objects with certain prescribed properties (for which explicit examples might be difficult to find) by observing that the probability of randomly selecting an object with those properties is greater than 0. This approach (often referred to astheprobabilistic method) proved highly effective in applications to extremal combinatorics and graph theory. A closely related area is the study of finiteMarkov chains,especially on combinatorial objects. Here again probabilistic tools are used to estimate themixing time.[clarification needed]

Often associated withPaul Erdős,who did the pioneering work on the subject, probabilistic combinatorics was traditionally viewed as a set of tools to study problems in other parts of combinatorics. The area recently grew to become an independent field of combinatorics.

Algebraic combinatorics

[edit]
Young diagramof theinteger partition(5, 4, 1).
Main article:Algebraic combinatorics

Algebraic combinatorics is an area ofmathematicsthat employs methods ofabstract algebra,notablygroup theoryandrepresentation theory,in various combinatorial contexts and, conversely, applies combinatorial techniques to problems inalgebra.Algebraic combinatorics has come to be seen more expansively as an area of mathematics where the interaction of combinatorial and algebraic methods is particularly strong and significant. Thus the combinatorial topics may beenumerativein nature or involvematroids,polytopes,partially ordered sets,orfinite geometries.On the algebraic side, besides group and representation theory,lattice theoryandcommutative algebraare common.

Combinatorics on words

[edit]
Construction of aThue–Morse infinite word.
Main article:Combinatorics on words

Combinatorics on words deals withformal languages.It arose independently within several branches of mathematics, includingnumber theory,group theoryandprobability.It has applications to enumerative combinatorics,fractal analysis,theoretical computer science,automata theory,andlinguistics.While many applications are new, the classicalChomsky–Schützenberger hierarchyof classes offormal grammarsis perhaps the best-known result in the field.

Geometric combinatorics

[edit]
Anicosahedron.
Main article:Geometric combinatorics

Geometric combinatorics is related toconvexanddiscrete geometry.It asks, for example, how many faces of each dimension aconvex polytopecan have.Metricproperties of polytopes play an important role as well, e.g. theCauchy theoremon the rigidity of convex polytopes. Special polytopes are also considered, such aspermutohedra,associahedraandBirkhoff polytopes.Combinatorial geometryis a historical name for discrete geometry.

It includes a number of subareas such aspolyhedral combinatorics(the study offacesofconvex polyhedra),convex geometry(the study ofconvex sets,in particular combinatorics of their intersections), anddiscrete geometry,which in turn has many applications tocomputational geometry.The study ofregular polytopes,Archimedean solids,andkissing numbersis also a part of geometric combinatorics. Special polytopes are also considered, such as thepermutohedron,associahedronandBirkhoff polytope.

Topological combinatorics

[edit]
Splitting a necklacewith two cuts.
Main article:Topological combinatorics

Combinatorial analogs of concepts and methods intopologyare used to studygraph coloring,fair division,partitions,partially ordered sets,decision trees,necklace problemsanddiscrete Morse theory.It should not be confused withcombinatorial topologywhich is an older name foralgebraic topology.

Arithmetic combinatorics

[edit]
Main article:Arithmetic combinatorics

Arithmetic combinatorics arose out of the interplay betweennumber theory,combinatorics,ergodic theory,andharmonic analysis.It is about combinatorial estimates associated with arithmetic operations (addition, subtraction, multiplication, and division).Additive number theory(sometimes also called additive combinatorics) refers to the special case when only the operations of addition and subtraction are involved. One important technique in arithmetic combinatorics is theergodic theoryofdynamical systems.

Infinitary combinatorics

[edit]
Main article:Infinitary combinatorics

Infinitary combinatorics, or combinatorial set theory, is an extension of ideas in combinatorics to infinite sets. It is a part ofset theory,an area ofmathematical logic,but uses tools and ideas from both set theory and extremal combinatorics. Some of the things studied includecontinuous graphsandtrees,extensions ofRamsey's theorem,andMartin's axiom.Recent developments concern combinatorics of thecontinuum[22]and combinatorics on successors of singular cardinals.[23]

Gian-Carlo Rotaused the namecontinuous combinatorics[24]to describegeometric probability,since there are many analogies betweencountingandmeasure.

[edit]
Kissing spheresare connected to bothcoding theoryanddiscrete geometry.

Combinatorial optimization

[edit]

Combinatorial optimizationis the study of optimization on discrete and combinatorial objects. It started as a part of combinatorics and graph theory, but is now viewed as a branch of applied mathematics and computer science, related tooperations research,algorithm theoryandcomputational complexity theory.

Coding theory

[edit]

Coding theorystarted as a part of design theory with early combinatorial constructions oferror-correcting codes.The main idea of the subject is to design efficient and reliable methods of data transmission. It is now a large field of study, part ofinformation theory.

Discrete and computational geometry

[edit]

Discrete geometry(also called combinatorial geometry) also began as a part of combinatorics, with early results onconvex polytopesandkissing numbers.With the emergence of applications of discrete geometry tocomputational geometry,these two fields partially merged and became a separate field of study. There remain many connections with geometric and topological combinatorics, which themselves can be viewed as outgrowths of the early discrete geometry.

Combinatorics and dynamical systems

[edit]

Combinatorial aspects of dynamical systemsis another emerging field. Here dynamical systems can be defined on combinatorial objects. See for example graph dynamical system.

Combinatorics and physics

[edit]

There are increasing interactions betweencombinatorics and physics,particularlystatistical physics.Examples include an exact solution of theIsing model,and a connection between thePotts modelon one hand, and thechromaticandTutte polynomialson the other hand.

See also

[edit]

Notes

[edit]
  1. ^Björner and Stanley, p. 2
  2. ^Lovász, László (1979).Combinatorial Problems and Exercises.North-Holland.ISBN978-0821842621.Archivedfrom the original on 2021-04-16.Retrieved2021-03-23.In my opinion, combinatorics is now growing out of this early stage.
  3. ^Pak, Igor."What is Combinatorics?".Archivedfrom the original on 17 October 2017.Retrieved1 November2017.
  4. ^Ryser 1963,p. 2
  5. ^Mirsky, Leon (1979),"Book Review"(PDF),Bulletin of the American Mathematical Society,New Series,1:380–388,doi:10.1090/S0273-0979-1979-14606-8,archived(PDF)from the original on 2021-02-26,retrieved2021-02-04
  6. ^Rota, Gian Carlo (1969).Discrete Thoughts.Birkhaüser. p. 50.doi:10.1007/978-0-8176-4775-9.ISBN978-0-8176-4775-9.... combinatorial theory has been the mother of several of the more active branches of today's mathematics, which have become independent.... The typical... case of this is algebraic topology (formerly known as combinatorial topology)
  7. ^Acerbi, F. (2003)."On the shoulders of Hipparchus".Archive for History of Exact Sciences.57(6): 465–502.doi:10.1007/s00407-003-0067-0.S2CID122758966.Archivedfrom the original on 2022-01-23.Retrieved2021-03-12.
  8. ^Stanley, Richard P.;"Hipparchus, Plutarch, Schröder, and Hough",American Mathematical Monthly104(1997), no. 4, 344–350.
  9. ^Habsieger, Laurent; Kazarian, Maxim; Lando, Sergei (1998). "On the Second Number of Plutarch".The American Mathematical Monthly.105(5): 446.doi:10.1080/00029890.1998.12004906.
  10. ^Netz, R.; Acerbi, F.; Wilson, N."Towards a reconstruction of Archimedes' Stomachion".Sciamvs.5:67–99.Archivedfrom the original on 2021-04-16.Retrieved2021-03-12.
  11. ^Hogendijk, Jan P. (1986)."Arabic Traces of Lost Works of Apollonius".Archive for History of Exact Sciences.35(3): 187–253.doi:10.1007/BF00357307.ISSN0003-9519.JSTOR41133783.S2CID121613986.Archivedfrom the original on 2021-04-18.Retrieved2021-03-26.
  12. ^Huxley, G. (1967)."Okytokion".Greek, Roman, and Byzantine Studies.8(3): 203.Archivedfrom the original on 2021-04-16.Retrieved2021-03-26.
  13. ^O'Connor, John J.;Robertson, Edmund F.,"Combinatorics",MacTutor History of Mathematics Archive,University of St Andrews
  14. ^Puttaswamy, Tumkur K. (2000). "The Mathematical Accomplishments of Ancient Indian Mathematicians". In Selin, Helaine (ed.).Mathematics Across Cultures: The History of Non-Western Mathematics.Netherlands: Kluwer Academic Publishers. p. 417.ISBN978-1-4020-0260-1.Archivedfrom the original on 2021-04-16.Retrieved2015-11-15.
  15. ^Biggs, Norman L. (1979)."The Roots of Combinatorics".Historia Mathematica.6(2): 109–136.doi:10.1016/0315-0860(79)90074-0.
  16. ^Maistrov, L.E. (1974),Probability Theory: A Historical Sketch,Academic Press, p. 35,ISBN978-1-4832-1863-2,archivedfrom the original on 2021-04-16,retrieved2015-01-25.(Translation from 1967 Russian ed.)
  17. ^White, Arthur T. (1987). "Ringing the Cosets".The American Mathematical Monthly.94(8): 721–746.doi:10.1080/00029890.1987.12000711.
  18. ^White, Arthur T. (1996). "Fabian Stedman: The First Group Theorist?".The American Mathematical Monthly.103(9): 771–778.doi:10.1080/00029890.1996.12004816.
  19. ^SeeJournals in Combinatorics and Graph TheoryArchived2021-02-17 at theWayback Machine
  20. ^Sanders, Daniel P.;2-Digit MSC ComparisonArchived2008-12-31 at theWayback Machine
  21. ^Stinson 2003,pg.1
  22. ^Andreas Blass,Combinatorial Cardinal Characteristics of the Continuum,Chapter 6 in Handbook of Set Theory, edited byMatthew ForemanandAkihiro Kanamori,Springer, 2010
  23. ^Eisworth, Todd (2010), Foreman, Matthew; Kanamori, Akihiro (eds.),"Successors of Singular Cardinals",Handbook of Set Theory,Dordrecht: Springer Netherlands, pp. 1229–1350,doi:10.1007/978-1-4020-5764-9_16,ISBN978-1-4020-4843-2,retrieved2022-08-27
  24. ^"Continuous and profinite combinatorics"(PDF).Archived(PDF)from the original on 2009-02-26.Retrieved2009-01-03.

References

[edit]
[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Combinatorics&oldid=1255744814"