Cubic field

Inmathematics,specifically the area ofalgebraic number theory,acubic fieldis analgebraic number fieldofdegreethree.

Definition

IfKis afield extensionof therational numbersQofdegree[K:Q] = 3, thenKis called acubic field.Any suchfieldisisomorphicto a field of the form

\mathbf {Q} [x]/(f(x))

wherefis anirreducible cubic polynomialwithcoefficientsinQ.Iffhas threereal roots,thenKis called atotally real cubic fieldand it is an example of atotally real field.If, on the other hand,fhas a non-real root, thenKis called acomplex cubic field.

A cubic fieldKis called acyclic cubic fieldif it contains all three roots of its generating polynomialf.Equivalently,Kis a cyclic cubic field if it is aGalois extensionofQ,in which case itsGalois groupoverQiscyclicoforderthree. This can only happen ifKis totally real. It is a rare occurrence in the sense that if the set of cubic fields is ordered bydiscriminant,then the proportion of cubic fields which are cyclic approaches zero as the bound on the discriminant approaches infinity.^[1]

A cubic field is called apure cubic fieldif it can be obtained by adjoining the realcube root ${\sqrt[{3}]{n}}$ of acube-free positive integernto the rational number fieldQ.Such fields are always complex cubic fields since each positive number has twocomplexnon-real cube roots.

Examples

Adjoining the real cube root of 2 to the rational numbers gives the cubic field $\mathbf {Q} ({\sqrt[{3}]{2}})$ .This is an example of a pure cubic field, and hence of a complex cubic field. In fact, of all pure cubic fields, it has the smallest discriminant (inabsolute value), namely −108.^[2]
The complex cubic field obtained by adjoining toQa root ofx³+x²− 1is not pure. It has the smallest discriminant (in absolute value) of all cubic fields, namely −23.^[3]
Adjoining a root ofx³+x²− 2x− 1toQyields a cyclic cubic field, and hence a totally real cubic field. It has the smallest discriminant of all totally real cubic fields, namely 49.^[4]
The field obtained by adjoining toQa root ofx³+x²− 3x− 1is an example of a totally real cubic field that is not cyclic. Its discriminant is 148, the smallest discriminant of a non-cyclic totally real cubic field.^[5]
Nocyclotomic fieldsare cubic because the degree of a cyclotomic field is equal to φ(n), where φ isEuler's totient function,which only takes onevenvalues except for φ(1) = φ(2) = 1.

Galois closure

A cyclic cubic fieldKis its ownGalois closurewith Galois group Gal(K/Q) isomorphic to thecyclic groupof order three. However, any other cubic fieldKis a non-Galois extension ofQand has a field extensionNof degree two as its Galois closure. The Galois group Gal(N/Q) is isomorphic to thesymmetric groupS₃on three letters.

Associated quadratic field

The discriminant of a cubic fieldKcan be written uniquely asdf²wheredis afundamental discriminant.Then,Kis cyclicif and only ifd= 1, in which case the onlysubfieldofKisQitself. Ifd≠ 1 then the Galois closureNofKcontains a uniquequadratic fieldkwhose discriminant isd(in the cased= 1, the subfieldQis sometimes considered as the "degenerate" quadratic field of discriminant 1). TheconductorofNoverkisf,andf²is therelative discriminantofNoverK.The discriminant ofNisd³f⁴.^[6]^[7]

The fieldKis a pure cubic field if and only ifd= −3. This is the case for which the quadratic field contained in the Galois closure ofKis the cyclotomic field of cuberoots of unity.^[7]

Discriminant

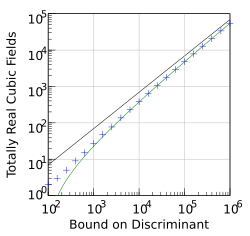
Since the sign of thediscriminantof a number fieldKis (−1)^r₂,wherer₂is the number of conjugate pairs of complex embeddings ofKintoC,the discriminant of a cubic field will be positive precisely when the field is totally real, and negative if it is a complex cubic field.

Given some real numberN> 0 there are only finitely many cubic fieldsKwhose discriminantD_Ksatisfies |D_K| ≤N.^[9]Formulae are known which calculate the prime decomposition ofD_K,and so it can be explicitly calculated.^[10]

Unlike quadratic fields, several non-isomorphic cubic fieldsK₁,...,K_mmay share the same discriminantD.The numbermof these fields is called themultiplicity^[11]of the discriminantD.Some small examples arem= 2 forD= −1836, 3969,m= 3 forD= −1228, 22356,m= 4 forD= −3299, 32009, andm= 6 forD= −70956, 3054132.

Any cubic fieldKwill be of the formK=Q(θ) for some number θ that is a root of an irreducible polynomial

f(X)=X^{3}-aX+b

whereaandbare integers. Thediscriminantoffis Δ = 4a³− 27b².Denoting the discriminant ofKbyD,theindexi(θ) of θ is then defined by Δ =i(θ)²D.

In the case of a non-cyclic cubic fieldKthis index formula can be combined with the conductor formulaD=f²dto obtain a decomposition of the polynomial discriminant Δ =i(θ)²f²dinto the square of the producti(θ)fand the discriminantdof the quadratic fieldkassociated with the cubic fieldK,wheredissquarefreeup to a possible factor 2²or 2³.Georgy Voronoygave a method for separatingi(θ) andfin the square part of Δ.^[12]

The study of the number of cubic fields whose discriminant is less than a given bound is a current area of research. LetN⁺(X) (respectivelyN⁻(X)) denote the number of totally real (respectively complex) cubic fields whose discriminant is bounded byXin absolute value. In the early 1970s,Harold DavenportandHans Heilbronndetermined the first term of the asymptotic behaviour ofN^±(X) (i.e. asXgoes to infinity).^[13]^[14]By means of an analysis of theresidueof theShintani zeta function,combined with a study of the tables of cubic fields compiled by Karim Belabas (Belabas 1997) and someheuristics,David P. Robertsconjectureda more precise asymptotic formula:^[15]

N^{\pm }(X)\sim {\frac {A_{\pm }}{12\zeta (3)}}X+{\frac {4\zeta ({\frac {1}{3}})B_{\pm }}{5\Gamma ({\frac {2}{3}})^{3}\zeta ({\frac {5}{3}})}}X^{\frac {5}{6}}

whereA_±= 1 or 3,B_±= 1 or ${\sqrt {3}}$ ,according to the totally real or complex case, ζ(s) is theRiemann zeta function,and Γ(s) is theGamma function.Proofs of this formula have been published byBhargava, Shankar & Tsimerman (2013)using methods based on Bhargava's earlier work, as well as byTaniguchi & Thorne (2013)based on the Shintani zeta function.

Unit group

According toDirichlet's unit theorem,the torsion-free unit rankrof an algebraic number fieldKwithr₁real embeddings andr₂pairs of conjugate complex embeddings is determined by the formular=r₁+r₂− 1. Hence a totally real cubic fieldKwithr₁= 3,r₂= 0 has two independent units ε₁,ε₂and a complex cubic fieldKwithr₁=r₂= 1 has a single fundamental unit ε₁.These fundamental systems of units can be calculated by means of generalizedcontinued fractionalgorithms byVoronoi,^[16]which have been interpreted geometrically byDeloneandFaddeev.^[17]

Notes

^Harvey Cohn computed an asymptotic for the number of cyclic cubic fields (Cohn 1954), whileHarold DavenportandHans Heilbronncomputed the asymptotic for all cubic fields (Davenport & Heilbronn 1971).
^Cohen 1993,§B.3 contains a table of complex cubic fields
^Cohen 1993,§B.3
^Cohen 1993,§B.4 contains a table of totally real cubic fields and indicates which are cyclic
^Cohen 1993,§B.4
^Hasse 1930
^^a ^bCohen 1993,§6.4.5
^^a ^bThe exact counts were computed by Michel Olivier and are available at[1].The first-order asymptotic is due toHarold DavenportandHans Heilbronn(Davenport & Heilbronn 1971). The second-order term was conjectured by David P. Roberts (Roberts 2001) and a proof has been published byManjul Bhargava,Arul Shankar, andJacob Tsimerman(Bhargava, Shankar & Tsimerman 2013).
^H. Minkowski,Diophantische Approximationen,chapter 4, §5.
^Llorente, P.; Nart, E. (1983)."Effective determination of the decomposition of the rational primes in a cubic field".Proceedings of the American Mathematical Society.87(4): 579–585.doi:10.1090/S0002-9939-1983-0687621-6.
^Mayer, D. C. (1992)."Multiplicities of dihedral discriminants".Math. Comp.58(198): 831–847 and S55–S58.Bibcode:1992MaCom..58..831M.doi:10.1090/S0025-5718-1992-1122071-3.
^G. F. Voronoi,Concerning algebraic integers derivable from a root of an equation of the third degree,Master's Thesis, St. Petersburg, 1894 (Russian).
^Davenport & Heilbronn 1971
^Their work can also be interpreted as a computation of the average size of the3-torsionpart of theclass groupof aquadratic field,and thus constitutes one of the few proven cases of theCohen–Lenstra conjectures:see, e.g.Bhargava, Manjul;Varma, Ila (2014),The mean number of 3-torsion elements in the class groups and ideal groups of quadratic orders,arXiv:1401.5875,Bibcode:2014arXiv1401.5875B,This theorem [of Davenport and Heilbronn] yields the only two proven cases of the Cohen-Lenstra heuristics for class groups of quadratic fields.
^Roberts 2001,Conjecture 3.1
^Voronoi, G. F. (1896).On a generalization of the algorithm of continued fractions(in Russian). Warsaw: Doctoral Dissertation.
^Delone, B. N.; Faddeev, D. K. (1964).The theory of irrationalities of the third degree.Translations of Mathematical Monographs. Vol. 10. Providence, Rhode Island: American Mathematical Society.

References

Şaban Alaca, Kenneth S. Williams,Introductory algebraic number theory,Cambridge University Press,2004.
Belabas, Karim (1997), "A fast algorithm to compute cubic fields",Mathematics of Computation,66(219): 1213–1237,doi:10.1090/s0025-5718-97-00846-6,MR 1415795
Bhargava, Manjul;Shankar, Arul; Tsimerman, Jacob (2013), "On the Davenport–Heilbronn theorem and second order terms",Inventiones Mathematicae,193(2): 439–499,arXiv:1005.0672,Bibcode:2013InMat.193..439B,doi:10.1007/s00222-012-0433-0,MR 3090184,S2CID 253738365
Cohen, Henri(1993),A Course in Computational Algebraic Number Theory,Graduate Texts in Mathematics, vol. 138, Berlin, New York:Springer-Verlag,ISBN 978-3-540-55640-4,MR 1228206
Cohn, Harvey (1954), "The density of abelian cubic fields",Proceedings of the American Mathematical Society,5(3): 476–477,doi:10.2307/2031963,JSTOR 2031963,MR 0064076
Davenport, Harold;Heilbronn, Hans(1971), "On the density of discriminants of cubic fields. II",Proceedings of the Royal Society A,322(1551): 405–420,Bibcode:1971RSPSA.322..405D,doi:10.1098/rspa.1971.0075,MR 0491593,S2CID 122814162
Hasse, Helmut(1930), "Arithmetische Theorie der kubischen Zahlkörper auf klassenkörpertheoretischer Grundlage",Mathematische Zeitschrift(in German),31(1): 565–582,doi:10.1007/BF01246435,S2CID 121649559
Roberts, David P. (2001), "Density of cubic field discriminants",Mathematics of Computation,70(236): 1699–1705,arXiv:math/9904190,doi:10.1090/s0025-5718-00-01291-6,MR 1836927,S2CID 7524750
Taniguchi, Takashi; Thorne, Frank (2013), "Secondary terms in counting functions for cubic fields",Duke Mathematical Journal,162(13): 2451–2508,arXiv:1102.2914,doi:10.1215/00127094-2371752,MR 3127806,S2CID 16463250

External links

Media related toCubic fieldat Wikimedia Commons

[1] Harvey Cohn computed an asymptotic for the number of cyclic cubic fields (Cohn 1954), whileHarold DavenportandHans Heilbronncomputed the asymptotic for all cubic fields (Davenport & Heilbronn 1971).

[2] Cohen 1993,§B.3 contains a table of complex cubic fields

[3] Cohen 1993,§B.3

[4] Cohen 1993,§B.4 contains a table of totally real cubic fields and indicates which are cyclic

[5] Cohen 1993,§B.4

[6] Hasse 1930

[Cohen_1993_loc=§6.4.5-7] Cohen 1993,§6.4.5

[discdata-8] The exact counts were computed by Michel Olivier and are available at[1].The first-order asymptotic is due toHarold DavenportandHans Heilbronn(Davenport & Heilbronn 1971). The second-order term was conjectured by David P. Roberts (Roberts 2001) and a proof has been published byManjul Bhargava,Arul Shankar, andJacob Tsimerman(Bhargava, Shankar & Tsimerman 2013).

[9] H. Minkowski,Diophantische Approximationen,chapter 4, §5.

[10] Llorente, P.; Nart, E. (1983)."Effective determination of the decomposition of the rational primes in a cubic field".Proceedings of the American Mathematical Society.87(4): 579–585.doi:10.1090/S0002-9939-1983-0687621-6.

[11] Mayer, D. C. (1992)."Multiplicities of dihedral discriminants".Math. Comp.58(198): 831–847 and S55–S58.Bibcode:1992MaCom..58..831M.doi:10.1090/S0025-5718-1992-1122071-3.

[12] G. F. Voronoi,Concerning algebraic integers derivable from a root of an equation of the third degree,Master's Thesis, St. Petersburg, 1894 (Russian).

[13] Davenport & Heilbronn 1971

[14] Their work can also be interpreted as a computation of the average size of the3-torsionpart of theclass groupof aquadratic field,and thus constitutes one of the few proven cases of theCohen–Lenstra conjectures:see, e.g.Bhargava, Manjul;Varma, Ila (2014),The mean number of 3-torsion elements in the class groups and ideal groups of quadratic orders,arXiv:1401.5875,Bibcode:2014arXiv1401.5875B,This theorem [of Davenport and Heilbronn] yields the only two proven cases of the Cohen-Lenstra heuristics for class groups of quadratic fields.

[15] Roberts 2001,Conjecture 3.1

[16] Voronoi, G. F. (1896).On a generalization of the algorithm of continued fractions(in Russian). Warsaw: Doctoral Dissertation.

[17] Delone, B. N.; Faddeev, D. K. (1964).The theory of irrationalities of the third degree.Translations of Mathematical Monographs. Vol. 10. Providence, Rhode Island: American Mathematical Society.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]