Square root

"Square roots" redirects here. For other uses, seeSquare Roots (disambiguation).

Notation for the (principal) square root ofx.

For example,√25= 5,since25 = 5 ⋅ 5,or5²(5 squared).

Inmathematics,asquare rootof a numberxis a numberysuch that$y^{2}=x$;in other words, a numberywhosesquare(the result of multiplying the number by itself, or$y\cdot y$) isx.For example, 4 and −4 are square roots of 16 because$4^{2}=(-4)^{2}=16$.

Everynonnegativereal numberxhas a unique nonnegative square root, called theprincipal square rootor simplythe square root(with a definite article, see below), which is denoted by${\sqrt {x}},$where the symbol "${\sqrt {~^{~}}}$"is called theradical signorradix.For example, to express the fact that the principal square root of 9 is 3, we write${\sqrt {9}}=3$.The term (or number) whose square root is being considered is known as theradicand.The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negativex,the principal square root can also be written inexponentnotation, as$x^{1/2}$.

Everypositive numberxhas two square roots:${\sqrt {x}}$(which is positive) and$-{\sqrt {x}}$(which is negative). The two roots can be written more concisely using the± signas$\pm {\sqrt {x}}$.Although the principal square root of a positive number is only one of its two square roots, the designation "thesquare root "is often used to refer to the principal square root.

Square roots of negative numbers can be discussed within the framework ofcomplex numbers.More generally, square roots can be considered in any context in which a notion of the "square"of a mathematical object is defined. These includefunction spacesandsquare matrices,among othermathematical structures.

History

YBC 7289 clay tablet

TheYale Babylonian Collectionclay tabletYBC 7289was created between 1800 BC and 1600 BC, showing${\sqrt {2}}$and${\textstyle {\frac {\sqrt {2}}{2}}={\frac {1}{\sqrt {2}}}}$respectively as 1;24,51,10 and 0;42,25,35base 60numbers on a square crossed by two diagonals.(1;24,51,10) base 60 corresponds to 1.41421296, which is correct to 5 decimal places (1.41421356...).

TheRhind Mathematical Papyrusis a copy from 1650 BC of an earlierBerlin Papyrusand other texts – possibly theKahun Papyrus– that shows how the Egyptians extracted square roots by an inverse proportion method.

InAncient India,the knowledge of theoretical and applied aspects of square and square root was at least as old as theSulba Sutras,dated around 800–500 BC (possibly much earlier).A method for finding very good approximations to the square roots of 2 and 3 are given in theBaudhayana Sulba Sutra.Apastambawho was dated around 600 BCE has given a strikingly accurate value for${\sqrt {2}}$which is correct up to five decimal places as${\textstyle 1+{\frac {1}{3}}+{\frac {1}{3\times 4}}-{\frac {1}{3\times 4\times 34}}}$. Aryabhata,in theAryabhatiya(section 2.4), has given a method for finding the square root of numbers having many digits.

It was known to the ancient Greeks that square roots ofpositive integersthat are notperfect squaresare alwaysirrational numbers:numbers not expressible as aratioof two integers (that is, they cannot be written exactly as${\frac {m}{n}}$,wheremandnare integers). This is the theoremEuclid X, 9,almost certainly due toTheaetetusdating back toc. 380 BC. The discovery of irrational numbers, including the particular case of thesquare root of 2,is widely associated with the Pythagorean school.Although some accounts attribute the discovery toHippasus,the specific contributor remains uncertain due to the scarcity of primary sources and the secretive nature of the brotherhood.It is exactly the length of thediagonalof asquare with side length 1.

In the Chinese mathematical workWritings on Reckoning,written between 202 BC and 186 BC during the earlyHan dynasty,the square root is approximated by using an "excess and deficiency" method, which says to "...combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend."

A symbol for square roots, written as an elaborate R, was invented byRegiomontanus(1436–1476). An R was also used for radix to indicate square roots inGerolamo Cardano'sArs Magna.

According to historian of mathematicsD.E. Smith,Aryabhata's method for finding the square root was first introduced in Europe byCataneo—in 1546.

According to Jeffrey A. Oaks, Arabs used the letterjīm/ĝīm(ج), the first letter of the word "جذر"(variously transliterated asjaḏr,jiḏr,ǧaḏrorǧiḏr,"root" ), placed in its initial form (ﺟ) over a number to indicate its square root. The letterjīmresembles the present square root shape. Its usage goes as far as the end of the twelfth century in the works of the Moroccan mathematicianIbn al-Yasamin.

The symbol "√" for the square root was first used in print in 1525, inChristoph Rudolff'sCoss.

Properties and uses

The graph of the functionf(x) = √x,made up of half aparabolawith a verticaldirectrix

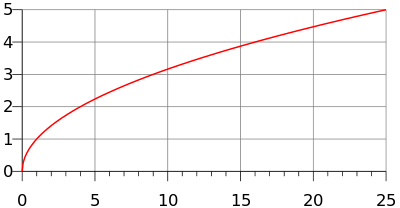
The principal square root function$f(x)={\sqrt {x}}$(usually just referred to as the "square root function" ) is afunctionthat maps thesetof nonnegative real numbers onto itself. Ingeometricalterms, the square root function maps theareaof a square to its side length.

The square root ofxis rational if and only ifxis arational numberthat can be represented as a ratio of two perfect squares. (Seesquare root of 2for proofs that this is an irrational number, andquadratic irrationalfor a proof for all non-square natural numbers.) The square root function maps rational numbers intoalgebraic numbers,the latter being asupersetof the rational numbers).

For all real numbersx, $${\sqrt {x^{2}}}=\left|x\right|={\begin{cases}x,&{\text{if }}x\geq 0\\-x,&{\text{if }}x<0.\end{cases}}$$(seeabsolute value).

For all nonnegative real numbersxandy, $${\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}$$ and $${\sqrt {x}}=x^{1/2}.$$

The square root function iscontinuousfor all nonnegativex,anddifferentiablefor all positivex.Iffdenotes the square root function, whose derivative is given by: $$f'(x)={\frac {1}{2{\sqrt {x}}}}.$$

TheTaylor seriesof${\sqrt {1+x}}$aboutx= 0converges for|x| ≤ 1,and is given by

$${\sqrt {1+x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\cdots,$$

The square root of a nonnegative number is used in the definition ofEuclidean norm(anddistance), as well as in generalizations such asHilbert spaces.It defines an important concept ofstandard deviationused inprobability theoryandstatistics.It has a major use in the formula for solutions of aquadratic equation.Quadratic fieldsand rings ofquadratic integers,which are based on square roots, are important in algebra and have uses in geometry. Square roots frequently appear in mathematical formulas elsewhere, as well as in manyphysicallaws.

Square roots of positive integers

A positive number has two square roots, one positive, and one negative, which areoppositeto each other. When talking ofthesquare root of a positive integer, it is usually the positive square root that is meant.

The square roots of an integer arealgebraic integers—more specificallyquadratic integers.

The square root of a positive integer is the product of the roots of itsprimefactors, because the square root of a product is the product of the square roots of the factors. Since${\textstyle {\sqrt {p^{2k}}}=p^{k},}$only roots of those primes having an odd power in thefactorizationare necessary. More precisely, the square root of a prime factorization is $${\sqrt {p_{1}^{2e_{1}+1}\cdots p_{k}^{2e_{k}+1}p_{k+1}^{2e_{k+1}}\dots p_{n}^{2e_{n}}}}=p_{1}^{e_{1}}\dots p_{n}^{e_{n}}{\sqrt {p_{1}\dots p_{k}}}.$$

As decimal expansions

The square roots of theperfect squares(e.g., 0, 1, 4, 9, 16) areintegers.In all other cases, the square roots of positive integers areirrational numbers,and hence have non-repeating decimalsin theirdecimal representations.Decimal approximations of the square roots of the first few natural numbers are given in the following table.

n	${\sqrt {n}},$truncated to 50 decimal places
0	0
1	1
2	1.41421356237309504880168872420969807856967187537694
3	1.73205080756887729352744634150587236694280525381038
4	2
5	2.23606797749978969640917366873127623544061835961152
6	2.44948974278317809819728407470589139196594748065667
7	2.64575131106459059050161575363926042571025918308245
8	2.82842712474619009760337744841939615713934375075389
9	3
10	3.16227766016837933199889354443271853371955513932521

As expansions in other numeral systems

As with before, the square roots of theperfect squares(e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers areirrational numbers,and therefore have non-repeating digits in any standardpositional notationsystem.

The square roots of small integers are used in both theSHA-1andSHA-2hash function designs to providenothing up my sleeve numbers.

As periodic continued fractions

One of the most intriguing results from the study ofirrational numbersascontinued fractionswas obtained byJoseph Louis Lagrangec. 1780.Lagrange found that the representation of the square root of any non-square positive integer as a continued fraction isperiodic.That is, a certain pattern of partial denominators repeats indefinitely in the continued fraction. In a sense these square roots are the very simplest irrational numbers, because they can be represented with a simple repeating pattern of integers.

${\sqrt {2}}$	= [1; 2, 2,...]
${\sqrt {3}}$	= [1; 1, 2, 1, 2,...]
${\sqrt {4}}$	= [2]
${\sqrt {5}}$	= [2; 4, 4,...]
${\sqrt {6}}$	= [2; 2, 4, 2, 4,...]
${\sqrt {7}}$	= [2; 1, 1, 1, 4, 1, 1, 1, 4,...]
${\sqrt {8}}$	= [2; 1, 4, 1, 4,...]
${\sqrt {9}}$	= [3]
${\sqrt {10}}$	= [3; 6, 6,...]
${\sqrt {11}}$	= [3; 3, 6, 3, 6,...]
${\sqrt {12}}$	= [3; 2, 6, 2, 6,...]
${\sqrt {13}}$	= [3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6,...]
${\sqrt {14}}$	= [3; 1, 2, 1, 6, 1, 2, 1, 6,...]
${\sqrt {15}}$	= [3; 1, 6, 1, 6,...]
${\sqrt {16}}$	= [4]
${\sqrt {17}}$	= [4; 8, 8,...]
${\sqrt {18}}$	= [4; 4, 8, 4, 8,...]
${\sqrt {19}}$	= [4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8,...]
${\sqrt {20}}$	= [4; 2, 8, 2, 8,...]

Thesquare bracketnotation used above is a short form for a continued fraction. Written in the more suggestive algebraic form, the simple continued fraction for the square root of 11, [3; 3, 6, 3, 6,...], looks like this: $${\sqrt {11}}=3+{\cfrac {1}{3+{\cfrac {1}{6+{\cfrac {1}{3+{\cfrac {1}{6+{\cfrac {1}{3+\ddots }}}}}}}}}}$$

where the two-digit pattern {3, 6} repeats over and over again in the partial denominators. Since11 = 3²+ 2,the above is also identical to the followinggeneralized continued fractions:

$${\sqrt {11}}=3+{\cfrac {2}{6+{\cfrac {2}{6+{\cfrac {2}{6+{\cfrac {2}{6+{\cfrac {2}{6+\ddots }}}}}}}}}}=3+{\cfrac {6}{20-1-{\cfrac {1}{20-{\cfrac {1}{20-{\cfrac {1}{20-{\cfrac {1}{20-\ddots }}}}}}}}}}.$$

Computation

Main article:Methods of computing square roots

Square roots of positive numbers are not in generalrational numbers,and so cannot be written as a terminating or recurring decimal expression. Therefore in general any attempt to compute a square root expressed in decimal form can only yield an approximation, though a sequence of increasingly accurate approximations can be obtained.

Mostpocket calculatorshave a square root key. Computerspreadsheetsand othersoftwareare also frequently used to calculate square roots. Pocket calculators typically implement efficient routines, such as theNewton's method(frequently with an initial guess of 1), to compute the square root of a positive real number.When computing square roots withlogarithm tablesorslide rules,one can exploit the identities $${\sqrt {a}}=e^{(\ln a)/2}=10^{(\log _{10}a)/2},$$ wherelnandlog₁₀are thenaturalandbase-10 logarithms.

By trial-and-error,one can square an estimate for${\sqrt {a}}$and raise or lower the estimate until it agrees to sufficient accuracy. For this technique it is prudent to use the identity $$(x+c)^{2}=x^{2}+2xc+c^{2},$$ as it allows one to adjust the estimatexby some amountcand measure the square of the adjustment in terms of the original estimate and its square.

The most commoniterative methodof square root calculation by hand is known as the "Babylonian method"or" Heron's method "after the first-century Greek philosopherHeron of Alexandria,who first described it. The method uses the same iterative scheme as theNewton–Raphson methodyields when applied to the functiony=f(x) =x²−a,using the fact that its slope at any point isdy/dx=f′(x) = 2x,but predates it by many centuries. The algorithm is to repeat a simple calculation that results in a number closer to the actual square root each time it is repeated with its result as the new input. The motivation is that ifxis an overestimate to the square root of a nonnegative real numberathena/xwill be an underestimate and so the average of these two numbers is a better approximation than either of them. However, theinequality of arithmetic and geometric meansshows this average is always an overestimate of the square root (as notedbelow), and so it can serve as a new overestimate with which to repeat the process, whichconvergesas a consequence of the successive overestimates and underestimates being closer to each other after each iteration. To findx:

1. Start with an arbitrary positive start valuex.The closer to the square root ofa,the fewer the iterations that will be needed to achieve the desired precision.
2. Replacexby the average(x+a/x) / 2betweenxanda/x.
3. Repeat from step 2, using this average as the new value ofx.

That is, if an arbitrary guess for${\sqrt {a}}$isx₀,andx_{n+ 1}= (x_n+a/x_n) / 2,then eachx_nis an approximation of${\sqrt {a}}$which is better for largenthan for smalln.Ifais positive, the convergence isquadratic,which means that in approaching the limit, the number of correct digits roughly doubles in each next iteration. Ifa= 0,the convergence is only linear; however,${\sqrt {0}}=0$so in this case no iteration is needed.

Using the identity $${\sqrt {a}}=2^{-n}{\sqrt {4^{n}a}},$$ the computation of the square root of a positive number can be reduced to that of a number in the range[1, 4).This simplifies finding a start value for the iterative method that is close to the square root, for which apolynomialorpiecewise-linearapproximationcan be used.

Thetime complexityfor computing a square root withndigits of precision is equivalent to that of multiplying twon-digit numbers.

Another useful method for calculating the square root is the shifting nth root algorithm, applied forn= 2.

The name of the square rootfunctionvaries fromprogramming languageto programming language, withsqrt(often pronounced "squirt") being common, used inCand derived languages likeC++,JavaScript,PHP,andPython.

Square roots of negative and complex numbers

First leaf of the complex square root

Second leaf of the complex square root

Using theRiemann surfaceof the square root, it is shown how the two leaves fit together

The square of any positive or negative number is positive, and the square of 0 is 0. Therefore, no negative number can have arealsquare root. However, it is possible to work with a more inclusive set of numbers, called thecomplex numbers,that does contain solutions to the square root of a negative number. This is done by introducing a new number, denoted byi(sometimes byj,especially in the context ofelectricitywhereitraditionally represents electric current) and called theimaginary unit,which isdefinedsuch thati²= −1.Using this notation, we can think ofias the square root of −1, but we also have(−i)²=i²= −1and so−iis also a square root of −1. By convention, the principal square root of −1 isi,or more generally, ifxis any nonnegative number, then the principal square root of−xis $${\sqrt {-x}}=i{\sqrt {x}}.$$

The right side (as well as its negative) is indeed a square root of−x,since $$(i{\sqrt {x}})^{2}=i^{2}({\sqrt {x}})^{2}=(-1)x=-x.$$

For every non-zero complex numberzthere exist precisely two numberswsuch thatw²=z:the principal square root ofz(defined below), and its negative.

Principal square root of a complex number

Geometric representation of the 2nd to 6th roots of a complex numberz,in polar formre^iφ wherer= |z |andφ= argz.Ifzis real,φ= 0orπ.Principal roots are shown in black.

To find a definition for the square root that allows us to consistently choose a single value, called theprincipal value,we start by observing that any complex number$x+iy$can be viewed as a point in the plane,$(x,y),$expressed usingCartesian coordinates.The same point may be reinterpreted usingpolar coordinatesas the pair$(r,\varphi ),$where$r\geq 0$is the distance of the point from the origin, and$\varphi$is the angle that the line from the origin to the point makes with the positive real ($x$) axis. In complex analysis, the location of this point is conventionally written$re^{i\varphi }.$If $$z=re^{i\varphi }{\text{ with }}-\pi <\varphi \leq \pi,$$ then theprincipal square rootof$z$is defined to be the following: $${\sqrt {z}}={\sqrt {r}}e^{i\varphi /2}.$$ The principal square root function is thus defined using the non-positive real axis as abranch cut.If$z$is a non-negative real number (which happens if and only if$\varphi =0$) then the principal square root of$z$is${\sqrt {r}}e^{i(0)/2}={\sqrt {r}};$in other words, the principal square root of a non-negative real number is just the usual non-negative square root. It is important that$-\pi <\varphi \leq \pi$because if, for example,$z=-2i$(so$\varphi =-\pi /2$) then the principal square root is $${\sqrt {-2i}}={\sqrt {2e^{i\varphi }}}={\sqrt {2}}e^{i\varphi /2}={\sqrt {2}}e^{i(-\pi /4)}=1-i$$ but using${\tilde {\varphi }}:=\varphi +2\pi =3\pi /2$would instead produce the other square root${\sqrt {2}}e^{i{\tilde {\varphi }}/2}={\sqrt {2}}e^{i(3\pi /4)}=-1+i=-{\sqrt {-2i}}.$

The principal square root function isholomorphiceverywhere except on the set of non-positive real numbers (on strictly negative reals it is not evencontinuous). The above Taylor series for${\sqrt {1+x}}$remains valid for complex numbers$x$with$|x|<1.$

The above can also be expressed in terms oftrigonometric functions: $${\sqrt {r\left(\cos \varphi +i\sin \varphi \right)}}={\sqrt {r}}\left(\cos {\frac {\varphi }{2}}+i\sin {\frac {\varphi }{2}}\right).$$

Algebraic formula

The square roots ofi

When the number is expressed using its real and imaginary parts, the following formula can be used for the principal square root:

$${\sqrt {x+iy}}={\sqrt {{\tfrac {1}{2}}{\bigl (}{\sqrt {\textstyle x^{2}+y^{2}}}+x{\bigr )}}}+i\operatorname {sgn}(y){\sqrt {{\tfrac {1}{2}}{\bigl (}{\sqrt {\textstyle x^{2}+y^{2}}}-x{\bigr )}}},$$

wheresgn(y) = 1ify≥ 0andsgn(y) = −1otherwise.In particular, the imaginary parts of the original number and the principal value of its square root have the same sign. The real part of the principal value of the square root is always nonnegative.

For example, the principal square roots of±iare given by:

$${\sqrt {i}}={\frac {1+i}{\sqrt {2}}},\qquad {\sqrt {-i}}={\frac {1-i}{\sqrt {2}}}.$$

Notes

In the following, the complexzandwmay be expressed as:

• $z=|z|e^{i\theta _{z}}$
• $w=|w|e^{i\theta _{w}}$

where$-\pi <\theta _{z}\leq \pi$and$-\pi <\theta _{w}\leq \pi$.

Because of the discontinuous nature of the square root function in the complex plane, the following laws arenot truein general.

• ${\sqrt {zw}}={\sqrt {z}}{\sqrt {w}}$
  Counterexample for the principal square root:z= −1andw= −1
  This equality is valid only when$-\pi <\theta _{z}+\theta _{w}\leq \pi$
• ${\frac {\sqrt {w}}{\sqrt {z}}}={\sqrt {\frac {w}{z}}}$
  Counterexample for the principal square root:w= 1andz= −1
  This equality is valid only when$-\pi <\theta _{w}-\theta _{z}\leq \pi$
• ${\sqrt {z^{*}}}=\left({\sqrt {z}}\right)^{*}$
  Counterexample for the principal square root:z= −1)
  This equality is valid only when$\theta _{z}\neq \pi$

A similar problem appears with other complex functions with branch cuts, e.g., thecomplex logarithmand the relationslogz+ logw= log(zw)orlog(z^*) = log(z)^*which are not true in general.

Wrongly assuming one of these laws underlies several faulty "proofs", for instance the following one showing that−1 = 1: $${\begin{aligned}-1&=i\cdot i\\&={\sqrt {-1}}\cdot {\sqrt {-1}}\\&={\sqrt {\left(-1\right)\cdot \left(-1\right)}}\\&={\sqrt {1}}\\&=1.\end{aligned}}$$

The third equality cannot be justified (seeinvalid proof).It can be made to hold by changing the meaning of √ so that this no longer represents the principal square root (see above) but selects a branch for the square root that contains${\sqrt {1}}\cdot {\sqrt {-1}}.$The left-hand side becomes either $${\sqrt {-1}}\cdot {\sqrt {-1}}=i\cdot i=-1$$ if the branch includes+ior $${\sqrt {-1}}\cdot {\sqrt {-1}}=(-i)\cdot (-i)=-1$$ if the branch includes−i,while the right-hand side becomes $${\sqrt {\left(-1\right)\cdot \left(-1\right)}}={\sqrt {1}}=-1,$$ where the last equality,${\sqrt {1}}=-1,$is a consequence of the choice of branch in the redefinition of√.

nth roots and polynomial roots

The definition of a square root of$x$as a number$y$such that$y^{2}=x$has been generalized in the following way.

Acube rootof$x$is a number$y$such that$y^{3}=x$;it is denoted${\sqrt[{3}]{x}}.$

Ifnis an integer greater than two, an-th rootof$x$is a number$y$such that$y^{n}=x$;it is denoted${\sqrt[{n}]{x}}.$

Given anypolynomialp,arootofpis a numberysuch thatp(y) = 0.For example, thenth roots ofxare the roots of the polynomial (iny)$y^{n}-x.$

Abel–Ruffini theoremstates that, in general, the roots of a polynomial of degree five or higher cannot be expressed in terms ofnth roots.

Square roots of matrices and operators

Main article:Square root of a matrix

See also:Square root of a 2 by 2 matrix

IfAis apositive-definite matrixor operator, then there exists precisely one positive definite matrix or operatorBwithB²=A;we then defineA^1/2=B.In general matrices may have multiple square roots or even an infinitude of them. For example, the2 × 2identity matrixhas an infinity of square roots,though only one of them is positive definite.

In integral domains, including fields

Each element of anintegral domainhas no more than 2 square roots. Thedifference of two squaresidentityu²−v²= (u−v)(u+v)is proved using thecommutativity of multiplication.Ifuandvare square roots of the same element, thenu²−v²= 0.Because there are nozero divisorsthis impliesu=voru+v= 0,where the latter means that two roots areadditive inversesof each other. In other words if an element a square rootuof an elementaexists, then the only square roots ofaareuand−u.The only square root of 0 in an integral domain is 0 itself.

In a field ofcharacteristic2, an element either has one square root or does not have any at all, because each element is its own additive inverse, so that−u=u.If the field isfiniteof characteristic 2 then every element has a unique square root. In afieldof any other characteristic, any non-zero element either has two square roots, as explained above, or does not have any.

Given an oddprime numberp,letq=p^efor some positive integere.A non-zero element of the fieldF_qwithqelements is aquadratic residueif it has a square root inF_q.Otherwise, it is a quadratic non-residue. There are(q− 1)/2quadratic residues and(q− 1)/2quadratic non-residues; zero is not counted in either class. The quadratic residues form agroupunder multiplication. The properties of quadratic residues are widely used innumber theory.

In rings in general

Unlike in an integral domain, a square root in an arbitrary (unital) ring need not be unique up to sign. For example, in the ring$\mathbb {Z} /8\mathbb {Z}$of integersmodulo 8(which is commutative, but has zero divisors), the element 1 has four distinct square roots: ±1 and ±3.

Another example is provided by the ring ofquaternions$\mathbb {H},$which has no zero divisors, but is not commutative. Here, the element −1 hasinfinitely many square roots,including±i,±j,and±k.In fact, the set of square roots of−1is exactly $$\{ai+bj+ck\mid a^{2}+b^{2}+c^{2}=1\}.$$

A square root of 0 is either 0 or a zero divisor. Thus in rings where zero divisors do not exist, it is uniquely 0. However, rings with zero divisors may have multiple square roots of 0. For example, in$\mathbb {Z} /n^{2}\mathbb {Z},$any multiple ofnis a square root of 0.

Geometric construction of the square root

Constructingthe length$x={\sqrt {a}}$,given the$a$and the unit length

TheSpiral of Theodorusup to the triangle with a hypotenuse of√17

Jay Hambidge's construction of successive square roots usingroot rectangles

The square root of a positive number is usually defined as the side length of asquarewith theareaequal to the given number. But the square shape is not necessary for it: if one of twosimilarplanar Euclideanobjects has the areaatimes greater than another, then the ratio of their linear sizes is${\sqrt {a}}$.

A square root can be constructed with a compass and straightedge. In hisElements,Euclid(fl.300 BC) gave the construction of thegeometric meanof two quantities in two different places:Proposition II.14andProposition VI.13.Since the geometric mean ofaandbis${\sqrt {ab}}$,one can construct${\sqrt {a}}$simply by takingb= 1.

The construction is also given byDescartesin hisLa Géométrie,see figure 2 onpage 2.However, Descartes made no claim to originality and his audience would have been quite familiar with Euclid.

Euclid's second proof in Book VI depends on the theory ofsimilar triangles.Let AHB be a line segment of lengtha+bwithAH =aandHB =b.Construct the circle with AB as diameter and let C be one of the two intersections of the perpendicular chord at H with the circle and denote the length CH ash.Then, usingThales' theoremand, as in theproof of Pythagoras' theorem by similar triangles,triangle AHC is similar to triangle CHB (as indeed both are to triangle ACB, though we don't need that, but it is the essence of the proof of Pythagoras' theorem) so that AH:CH is as HC:HB, i.e.a/h=h/b,from which we conclude by cross-multiplication thath²=ab,and finally that$h={\sqrt {ab}}$.When marking the midpoint O of the line segment AB and drawing the radius OC of length(a+b)/2,then clearly OC > CH, i.e.${\textstyle {\frac {a+b}{2}}\geq {\sqrt {ab}}}$(with equality if and only ifa=b), which is thearithmetic–geometric mean inequality for two variablesand, as notedabove,is the basis of theAncient Greekunderstanding of "Heron's method".

Another method of geometric construction usesright trianglesandinduction:${\sqrt {1}}$can be constructed, and once${\sqrt {x}}$has been constructed, the right triangle with legs 1 and${\sqrt {x}}$has ahypotenuseof${\sqrt {x+1}}$.Constructing successive square roots in this manner yields theSpiral of Theodorusdepicted above.

See also

• Apotome (mathematics)
• Cube root
• Functional square root
• Integer square root
• Nested radical
• Nth root
• Root of unity
• Solving quadratic equations with continued fractions
• Square-root sum problem
• Square root principle
• Quantum gate § Square root of NOT gate (√NOT)

References

• Dauben, Joseph W.(2007). "Chinese Mathematics I". In Katz, Victor J. (ed.).The Mathematics of Egypt, Mesopotamia, China, India, and Islam.Princeton: Princeton University Press.ISBN978-0-691-11485-9.
• Gel'fand, Izrael M.;Shen, Alexander (1993).Algebra(3rd ed.). Birkhäuser. p. 120.ISBN0-8176-3677-3.
• Joseph, George (2000).The Crest of the Peacock.Princeton: Princeton University Press.ISBN0-691-00659-8.
• Smith, David(1958).History of Mathematics.Vol. 2. New York: Dover Publications.ISBN978-0-486-20430-7.
• Selin, Helaine(2008),Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures,Springer,Bibcode:2008ehst.book.....S,ISBN978-1-4020-4559-2.

External links

• Algorithms, implementations, and more– Paul Hsieh's square roots webpage
• How to manually find a square root
• AMS Featured Column, Galileo's Arithmetic by Tony Philips– includes a section on how Galileo found square roots