Duoprism

Set of uniform $p-q$ duoprisms
Type	Prismatic uniform 4-polytopes
Schläfli symbol	${p}\times{q}$
Coxeter-Dynkin diagram
Cells	$p q$ -gonalprisms, $q p$ -gonal prisms
Faces	$pq$ squares, $p q$ -gons, $q p$ -gons
Edges	$2 pq$
Vertices	$pq$
Vertex figure	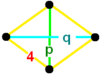disphenoid
Symmetry	$[p,2, q]$ ,order $4 pq$
Dual	$p-q$ duopyramid
Properties	convex,vertex-uniform

Set of uniform p-p duoprisms
Type	Prismatic uniform 4-polytope
Schläfli symbol	${p}\times{p}$
Coxeter-Dynkin diagram
Cells	$2 p p$ -gonalprisms
Faces	$p 2$ squares, $2 p p$ -gons
Edges	$2 p 2$
Vertices	$p 2$
Symmetry	$[p,2, p] = [2 p,2 +,2 p],$ order $8 p 2$
Dual	$p-p$ duopyramid
Properties	convex,vertex-uniform,Facet-transitive

Ingeometryof 4 dimensions or higher, adouble prism^[1]orduoprismis apolytoperesulting from theCartesian productof two polytopes, each of two dimensions or higher. The Cartesian product of an $n$ -polytope and an $m$ -polytope is an $(n + m)$ -polytope, where $n$ and $m$ are dimensions of 2 (polygon) or higher.

The lowest-dimensionalduoprismsexist in4-dimensional spaceas4-polytopesbeing the Cartesian product of two polygons in 2-dimensionalEuclidean space.More precisely, it is thesetof points:

P_{1}\times P_{2}=\{(x,y,z,w)|(x,y)\in P_{1},(z,w)\in P_{2}\}

where $P 1$ and $P 2$ are the sets of the points contained in the respective polygons. Such a duoprism isconvexif both bases are convex, and is bounded byprismatic cells.

Nomenclature

Four-dimensional duoprisms are considered to be prismatic 4-polytopes. A duoprism constructed from tworegular polygonsof the same edge length is auniform duoprism.

A duoprism made ofn-polygons andm-polygons is named by prefixing 'duoprism' with the names of the base polygons, for example: atriangular-pentagonal duoprismis the Cartesian product of a triangle and a pentagon.

An alternative, more concise way of specifying a particular duoprism is by prefixing with numbers denoting the base polygons, for example: 3,5-duoprism for the triangular-pentagonal duoprism.

Other alternative names:

q-gonal-p-gonal prism
q-gonal-p-gonal double prism
q-gonal-p-gonal hyperprism

The termduoprismis coined by George Olshevsky, shortened fromdouble prism.John Horton Conwayproposed a similar nameproprismforproduct prism,a Cartesian product of two or more polytopes of dimension at least two. The duoprisms are proprisms formed from exactly two polytopes.

Example 16-16 duoprism

Schlegel diagram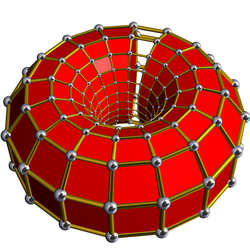 Projection from the center of one 16-gonal prism, and all but one of the opposite 16-gonal prisms are shown.	net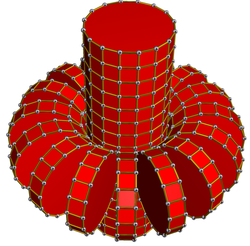 The two sets of 16-gonal prisms are shown. The top and bottom faces of the verticalcylinderare connected when folded together in 4D.

Geometry of 4-dimensional duoprisms

A 4-dimensionaluniformduoprismis created by the product of a regularn-sidedpolygonand a regularm-sided polygon with the same edge length. It is bounded bynm-gonalprismsandmn-gonal prisms. For example, the Cartesian product of a triangle and a hexagon is a duoprism bounded by 6 triangular prisms and 3 hexagonal prisms.

Whenmandnare identical, the resulting duoprism is bounded by 2nidenticaln-gonal prisms. For example, the Cartesian product of two triangles is a duoprism bounded by 6 triangular prisms.
Whenmandnare identically 4, the resulting duoprism is bounded by 8 square prisms (cubes), and is identical to thetesseract.

Them-gonal prisms are attached to each other via theirm-gonal faces, and form a closed loop. Similarly, then-gonal prisms are attached to each other via theirn-gonal faces, and form a second loop perpendicular to the first. These two loops are attached to each other via their square faces, and are mutually perpendicular.

Asmandnapproach infinity, the corresponding duoprisms approach theduocylinder.As such, duoprisms are useful as non-quadricapproximations of the duocylinder.

Nets

3-3
3-4	4-4
3-5	4-5	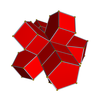5-5
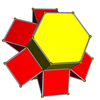3-6	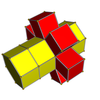4-6	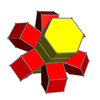5-6	6-6
3-7	4-7	5-7	6-7	7-7
3-8	4-8	5-8	6-8	7-8	8-8
3-9	4-9	5-9	6-9	7-9	8-9	9-9
3-10	4-10	5-10	6-10	7-10	8-10	9-10	10-10

Perspective projections

A cell-centered perspective projection makes a duoprism look like atorus,with two sets of orthogonal cells, p-gonal and q-gonal prisms.

Schlegel diagrams
6-prism	6-6 duoprism

Ahexagonal prism,projected into the plane by perspective, centered on a hexagonal face, looks like a double hexagon connected by (distorted)squares.Similarly a 6-6 duoprism projected into 3D approximates atorus,hexagonal both in plan and in section.

The p-q duoprisms are identical to the q-p duoprisms, but look different in these projections because they are projected in the center of different cells.

Schlegel diagrams
3-3	3-4	3-5	3-6	3-7	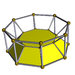3-8
4-3	4-4	4-5	4-6	4-7	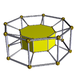4-8
5-3	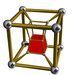5-4	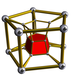5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Orthogonal projections

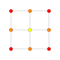
Vertex-centered orthogonal projections of p-p duoprisms project into [2n] symmetry for odd degrees, and [n] for even degrees. There are n vertices projected into the center. For 4,4, it represents the A₃Coxeter plane of thetesseract.The 5,5 projection is identical to the 3Drhombic triacontahedron.

Orthogonal projection wireframes of p-p duoprisms
Odd
3-3		5-5		7-7		9-9

[3]	[6]	[5]	[10]	[7]	[14]	[9]	[18]
Even
4-4(tesseract)		6-6		8-8		10-10

[4]	[8]	[6]	[12]	[8]	[16]	[10]	[20]

Related polytopes

Astereographic projectionof a rotatingduocylinder,divided into a checkerboard surface of squares from the {4,4|n} skew polyhedron

Theregular skew polyhedron,{4,4|n}, exists in 4-space as the n²square faces of an-n duoprism,using all 2n²edges and n²vertices. The 2nn-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are notregular.)

Duoantiprism

Like theantiprismsas alternatedprisms,there is a set of 4-dimensional duoantiprisms:4-polytopesthat can be created by analternationoperation applied to a duoprism. The alternated vertices create nonregular tetrahedral cells, except for the special case, the4-4 duoprism(tesseract) which creates the uniform (and regular)16-cell.The 16-cell is the only convex uniform duoantiprism.

The duoprisms,t_0,1,2,3{p,2,q}, can be alternated into,ht_0,1,2,3{p,2,q}, the "duoantiprisms", which cannot be made uniform in general. The only convex uniform solution is the trivial case of p=q=2, which is a lower symmetry construction of thetesseract,t_0,1,2,3{2,2,2}, with its alternation as the16-cell,,s{2}s{2}.

The only nonconvex uniform solution is p=5, q=5/3, ht_0,1,2,3{5,2,5/3},,constructed from 10pentagonal antiprisms,10pentagrammic crossed-antiprisms,and 50 tetrahedra, known as thegreat duoantiprism(gudap).^[2]^[3]

Ditetragoltriates

Also related are the ditetragoltriates or octagoltriates, formed by taking theoctagon(considered to be a ditetragon or a truncated square) to a p-gon. Theoctagonof a p-gon can be clearly defined if one assumes that the octagon is the convex hull of two perpendicularrectangles;then the p-gonal ditetragoltriate is the convex hull of two p-p duoprisms (where the p-gons are similar but not congruent, having different sizes) in perpendicular orientations. The resulting polychoron is isogonal and has 2p p-gonal prisms and p²rectangular trapezoprisms (acubewithD_2dsymmetry) but cannot be made uniform. The vertex figure is atriangular bipyramid.

Double antiprismoids

Like the duoantiprisms as alternated duoprisms, there is a set of p-gonal double antiprismoids created by alternating the 2p-gonal ditetragoltriates, creating p-gonal antiprisms and tetrahedra while reinterpreting the non-corealmic triangular bipyramidal spaces as two tetrahedra. The resulting figure is generally not uniform except for two cases: thegrand antiprismand its conjugate, the pentagrammic double antiprismoid (with p = 5 and 5/3 respectively), represented as the alternation of a decagonal or decagrammic ditetragoltriate. The vertex figure is a variant of thesphenocorona.

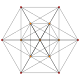
k_22 polytopes

The3-3 duoprism,-1₂₂,is first in a dimensional series of uniform polytopes, expressed byCoxeteras k₂₂series. The 3-3 duoprism is the vertex figure for the second, thebirectified 5-simplex.The fourth figure is a Euclidean honeycomb,2₂₂,and the final is a paracompact hyperbolic honeycomb, 3₂₂,with Coxeter group [3^2,2,3], ${\bar {T}}_{7}$ .Each progressiveuniform polytopeis constructed from the previous as itsvertex figure.

k₂₂figures in n dimensions
Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxeter group	A₂A₂	E₆	${\tilde {E}}_{6}$ =E₆⁺	${\bar {T}}_{7}$ =E₆⁺⁺
Coxeter diagram
Symmetry	[[3^2,2,-1]]	[[3^2,2,0]]	[[3^2,2,1]]	[[3^2,2,2]]	[[3^2,2,3]]
Order	72	1440	103,680	∞
Graph				∞	∞
Name	−1₂₂	0₂₂	1₂₂	2₂₂	3₂₂

Notes

^The Fourth Dimension Simply Explained,Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online:The Fourth Dimension Simply Explained—contains a description of duoprisms (double prisms) and duocylinders (double cylinders).Googlebook
^Jonathan Bowers - Miscellaneous Uniform Polychora965. Gudap
^http://www.polychora.com/12GudapsMovie.gif Archived2014-02-22 at theWayback MachineAnimation of cross sections

References

Regular Polytopes,H. S. M. Coxeter,Dover Publications, Inc., 1973, New York, p. 124.
Coxeter,The Beauty of Geometry: Twelve Essays,Dover Publications, 1999,ISBN0-486-40919-8(Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M.Regular Skew Polyhedra in Three and Four Dimensions.Proc. London Math. Soc. 43, 33-62, 1937.
John H. Conway,Heidi Burgiel, Chaim Goodman-Strauss,The Symmetries of Things2008,ISBN 978-1-56881-220-5(Chapter 26)
N.W. Johnson:The Theory of Uniform Polytopes and Honeycombs,Ph.D. Dissertation, University of Toronto, 1966

[1] The Fourth Dimension Simply Explained,Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online:The Fourth Dimension Simply Explained—contains a description of duoprisms (double prisms) and duocylinders (double cylinders).Googlebook

[2] Jonathan Bowers - Miscellaneous Uniform Polychora965. Gudap

[3] ttp://www.polychora.com/12GudapsMovie.gif Archived2014-02-22 at theWayback MachineAnimation of cross sections

[1]

[2]

[3]