Altitude (triangle)

"Orthocenter" and "Orthocentre" redirect here. For the orthocentric system, seeOrthocentric system.

The three altitudes of a triangle intersect at the orthocenter, which for anacute triangleis inside the triangle.

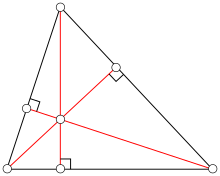
Ingeometry,analtitudeof atriangleis aline segmentthrough avertexandperpendicularto a line containingthe side opposite the vertex.This line containing the opposite side is called theextended baseof the altitude. The intersection of theextended baseand the altitude is called thefootof the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known asdropping the altitudeat that vertex. It is a special case oforthogonal projection.

Altitudes can be used in the computation of thearea of a triangle:one-half of the product of an altitude's length and its base's length equals the triangle's area. Thus, the longest altitude is perpendicular to the shortest side of the triangle. The altitudes are also related to the sides of the triangle through thetrigonometric functions.

In anisosceles triangle(a triangle with twocongruentsides), the altitude having the incongruent side as its base will have themidpointof that side as its foot. Also the altitude having the incongruent side as its base will be theangle bisectorof the vertex angle.

It is common to mark the altitude with the letterh(as inheight), often subscripted with the name of the side the altitude is drawn to.

The altitude of a right triangle from its right angle to its hypotenuse is the geometric mean of the lengths of the segments the hypotenuse is split into. UsingPythagoras' theoremon the 3 triangles of sides(p + q,r,s ),(r,p,h )and(s,h,q ),
${\begin{aligned}(p+q)^{2}\;\;&=\quad r^{2}\;\;\,+\quad s^{2}\\p^{2}\!\!+\!2pq\!+\!q^{2}&=\overbrace {p^{2}\!\!+\!h^{2}} +\overbrace {h^{2}\!\!+\!q^{2}} \\2pq\quad \;\;\;&=2h^{2}\;\therefore h\!=\!{\sqrt {pq}}\\\end{aligned}}$

In aright triangle,the altitude drawn to thehypotenusecdivides the hypotenuse into two segments of lengthspandq.If we denote the length of the altitude byh_c,we then have the relation

$h_{c}={\sqrt {pq}}$(Geometric mean theorem;seeSpecial Cases,inverse Pythagorean theorem)

In a right triangle, the altitude from each acute angle coincides with a leg and intersects the opposite side at (has its foot at) the right-angled vertex, which is the orthocenter.

For acute triangles, the feet of the altitudes all fall on the triangle's sides (not extended). In an obtuse triangle (one with anobtuse angle), the foot of the altitude to the obtuse-angled vertex falls in the interior of the opposite side, but the feet of the altitudes to the acute-angled vertices fall on the oppositeextended side,exterior to the triangle. This is illustrated in the adjacent diagram: in this obtuse triangle, an altitude dropped perpendicularly from the top vertex, which has an acute angle, intersects the extended horizontal side outside the triangle.

Orthocenter

See also:Orthocentric system

Three altitudes intersecting at the orthocenter

The three (possibly extended) altitudes intersect in a single point, called theorthocenterof the triangle, usually denoted byH.The orthocenter lies inside the triangleif and only ifthe triangle is acute. If one angle is a right angle, the orthocenter coincides with the vertex at the right angle.

LetA, B, Cdenote the vertices and also the angles of the triangle, and let$a=\left|{\overline {BC}}\right|,b=\left|{\overline {CA}}\right|,c=\left|{\overline {AB}}\right|$be the side lengths. The orthocenter hastrilinear coordinates

$${\begin{aligned}&\sec A:\sec B:\sec C\\&=\cos A-\sin B\sin C:\cos B-\sin C\sin A:\cos C-\sin A\sin B,\end{aligned}}$$

andbarycentric coordinates

$${\begin{aligned}&(a^{2}+b^{2}-c^{2})(a^{2}-b^{2}+c^{2}):(a^{2}+b^{2}-c^{2})(-a^{2}+b^{2}+c^{2}):(a^{2}-b^{2}+c^{2})(-a^{2}+b^{2}+c^{2})\\&=\tan A:\tan B:\tan C.\end{aligned}}$$

Since barycentric coordinates are all positive for a point in a triangle's interior but at least one is negative for a point in the exterior, and two of the barycentric coordinates are zero for a vertex point, the barycentric coordinates given for the orthocenter show that the orthocenter is in anacute triangle'sinterior, on the right-angled vertex of aright triangle,and exterior to anobtuse triangle.

In thecomplex plane,let the pointsA, B, Crepresent thenumbersz_A,z_B,z_Cand assume that thecircumcenterof triangle△ABCis located at the origin of the plane. Then, the complex number

$z_{H}=z_{A}+z_{B}+z_{C}$

is represented by the pointH,namely the altitude of triangle△ABC.From this, the following characterizations of the orthocenterHby means offree vectorscan be established straightforwardly:

${\vec {OH}}=\sum \limits _{\scriptstyle {\rm {cyclic}}}{\vec {OA}},\qquad 2\cdot {\vec {HO}}=\sum \limits _{\scriptstyle {\rm {cyclic}}}{\vec {HA}}.$

The first of the previous vector identities is also known as theproblem of Sylvester,proposed byJames Joseph Sylvester.

Properties

LetD, E, Fdenote the feet of the altitudes fromA, B, Crespectively. Then:

• The product of the lengths of the segments that the orthocenter divides an altitude into is the same for all three altitudes:

${\overline {AH}}\cdot {\overline {HD}}={\overline {BH}}\cdot {\overline {HE}}={\overline {CH}}\cdot {\overline {HF}}.$

The circle centered atHhaving radius the square root of this constant is the triangle'spolar circle.

• The sum of the ratios on the three altitudes of the distance of the orthocenter from the base to the length of the altitude is 1:(This property and the next one are applications of amore general propertyof any interior point and the threeceviansthrough it.)

${\frac {\overline {HD}}{\overline {AD}}}+{\frac {\overline {HE}}{\overline {BE}}}+{\frac {\overline {HF}}{\overline {CF}}}=1.$

• The sum of the ratios on the three altitudes of the distance of the orthocenter from the vertex to the length of the altitude is 2:

${\frac {\overline {AH}}{\overline {AD}}}+{\frac {\overline {BH}}{\overline {BE}}}+{\frac {\overline {CH}}{\overline {CF}}}=2.$

• Theisogonal conjugateof the orthocenter is thecircumcenterof the triangle.
• Theisotomic conjugateof the orthocenter is thesymmedian pointof theanticomplementary triangle.
• Four points in the plane, such that one of them is the orthocenter of the triangle formed by the other three, is called anorthocentric systemor orthocentric quadrangle.

Relation with circles and conics

Denote thecircumradiusof the triangle byR.Then

$a^{2}+b^{2}+c^{2}+{\overline {AH}}^{2}+{\overline {BH}}^{2}+{\overline {CH}}^{2}=12R^{2}.$

In addition, denotingras the radius of the triangle'sincircle,r_a,r_b,r_cas the radii of itsexcircles,andRagain as the radius of its circumcircle, the following relations hold regarding the distances of the orthocenter from the vertices:

${\begin{aligned}&r_{a}+r_{b}+r_{c}+r={\overline {AH}}+{\overline {BH}}+{\overline {CH}}+2R,\\&r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}={\overline {AH}}^{2}+{\overline {BH}}^{2}+{\overline {CH}}^{2}+(2R)^{2}.\end{aligned}}$

If any altitude, for example,AD,is extended to intersect the circumcircle atP,so thatADis a chord of the circumcircle, then the footDbisects segmentHP:

${\overline {HD}}={\overline {DP}}.$

Thedirectricesof allparabolasthat are externally tangent to one side of a triangle and tangent to the extensions of the other sides pass through the orthocenter.

Acircumconicpassing through the orthocenter of a triangle is arectangular hyperbola.

Relation to other centers, the nine-point circle

Main article:Nine-point circle

The orthocenterH,thecentroidG,thecircumcenterO,and the centerNof thenine-point circleall lie on a single line, known as theEuler line.The center of the nine-point circle lies at themidpointof the Euler line, between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half of that between the centroid and the orthocenter:

${\begin{aligned}&{\overline {OH}}=2{\overline {NH}},\\&2{\overline {OG}}={\overline {GH}}.\end{aligned}}$

The orthocenter is closer to theincenterIthan it is to the centroid, and the orthocenter is farther than the incenter is from the centroid:

${\begin{aligned}{\overline {HI}}&<{\overline {HG}},\\{\overline {HG}}&>{\overline {IG}}.\end{aligned}}$

In terms of the sidesa,b,c,inradiusrandcircumradiusR,

${\begin{aligned}{\overline {OH}}^{2}&=R^{2}-8R^{2}\cos A\cos B\cos C\\&=9R^{2}-(a^{2}+b^{2}+c^{2}),\\{\overline {HI}}^{2}&=2r^{2}-4R^{2}\cos A\cos B\cos C.\end{aligned}}$

Orthic triangle

Triangle△abc(respectively,△DEFin the text) is the orthic triangle of triangle△ABC

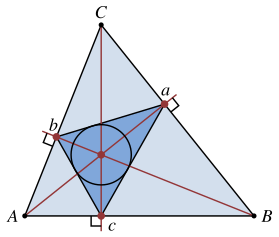
If the triangle△ABCisoblique(does not contain a right-angle), thepedal triangleof the orthocenter of the original triangle is called theorthic triangleoraltitude triangle.That is, the feet of the altitudes of an oblique triangle form the orthic triangle,△DEF.Also, the incenter (the center of the inscribed circle) of the orthic triangle△DEFis the orthocenter of the original triangle△ABC.

Trilinear coordinatesfor the vertices of the orthic triangle are given by

$${\begin{array}{rccccc}D=&0&:&\sec B&:&\sec C\\E=&\sec A&:&0&:&\sec C\\F=&\sec A&:&\sec B&:&0\end{array}}$$

Theextended sidesof the orthic triangle meet the opposite extended sides of its reference triangle at threecollinear points.

In anyacute triangle,the inscribed triangle with the smallest perimeter is the orthic triangle.This is the solution toFagnano's problem,posed in 1775.The sides of the orthic triangle are parallel to the tangents to the circumcircle at the original triangle's vertices.

The orthic triangle of an acute triangle gives a triangular light route.

The tangent lines of the nine-point circle at the midpoints of the sides of△ABCare parallel to the sides of the orthic triangle, forming a triangle similar to the orthic triangle.

The orthic triangle is closely related to thetangential triangle,constructed as follows: letL_Abe the line tangent to the circumcircle of triangle△ABCat vertexA,and defineL_B,L_Canalogously. Let$A''=L_{B}\cap L_{C},$$B''=L_{C}\cap L_{A},$$C''=L_{C}\cap L_{A}.$The tangential triangle is△A "B" C ",whose sides are the tangents to triangle△ABC's circumcircle at its vertices; it ishomotheticto the orthic triangle. The circumcenter of the tangential triangle, and thecenter of similitudeof the orthic and tangential triangles, are on theEuler line.

Trilinear coordinates for the vertices of the tangential triangle are given by

$${\begin{array}{rrcrcr}A''=&-a&:&b&:&c\\B''=&a&:&-b&:&c\\C''=&a&:&b&:&-c\end{array}}$$

The reference triangle and its orthic triangle areorthologic triangles.

For more information on the orthic triangle, seehere.

Some additional altitude theorems

Altitude in terms of the sides

For any triangle with sidesa, b, candsemiperimeter$s={\tfrac {1}{2}}(a+b+c),$the altitude from sidea(the base) is given by

$h_{a}={\frac {2{\sqrt {s(s-a)(s-b)(s-c)}}}{a}}.$

This follows from combiningHeron's formulafor the area of a triangle in terms of the sides with the area formula${\tfrac {1}{2}}\times {\text{base}}\times {\text{height}},$where the base is taken as sideaand the height is the altitude from the vertexA(opposite sidea).

By exchangingawithborc,this equation can also used to find the altitudesh_bandh_c,respectively.

Inradius theorems

Consider an arbitrary triangle with sidesa, b, cand with corresponding altitudesh_a,h_b,h_c.The altitudes and theincircleradiusrare related by

$\displaystyle {\frac {1}{r}}={\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}.$

Circumradius theorem

Denoting the altitude from one side of a triangle ash_a,the other two sides asbandc,and the triangle'scircumradius(radius of the triangle's circumscribed circle) asR,the altitude is given by

$h_{a}={\frac {bc}{2R}}.$

Interior point

Ifp₁,p₂,p₃are the perpendicular distances from any pointPto the sides, andh₁,h₂,h₃are the altitudes to the respective sides, then

${\frac {p_{1}}{h_{1}}}+{\frac {p_{2}}{h_{2}}}+{\frac {p_{3}}{h_{3}}}=1.$

Area theorem

Denoting the altitudes of any triangle from sidesa, b, crespectively ash_a,h_b,h_c,and denoting the semi-sum of the reciprocals of the altitudes as$H={\tfrac {h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1}}{2}}$we have

$\mathrm {Area} ^{-1}=4{\sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}.$

General point on an altitude

IfEis any point on an altitudeADof any triangle△ABC,then

${\overline {AC}}^{2}+{\overline {EB}}^{2}={\overline {AB}}^{2}+{\overline {CE}}^{2}.$

Triangle inequality

Since the area of the triangle is${\tfrac {1}{2}}ah_{a}={\tfrac {1}{2}}bh_{b}={\tfrac {1}{2}}ch_{c}$,the triangle inequality$a<b+c$implies

${\frac {1}{h_{a}}}<{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}$.

Special cases

Equilateral triangle

From any pointPwithin anequilateral triangle,the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. This isViviani's theorem.

Right triangle

Comparison of the inverse Pythagorean theorem with the Pythagorean theorem

In a right triangle with legsaandband hypotenusec,each of the legs is also an altitude:$h_{a}=b$and$h_{b}=a$.The third altitude can be found by the relation

${\frac {1}{h_{c}^{2}}}={\frac {1}{h_{a}^{2}}}+{\frac {1}{h_{b}^{2}}}={\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}.$

This is also known as theinverse Pythagorean theorem.

Note in particular:

${\begin{aligned}{\tfrac {1}{2}}AC\cdot BC&={\tfrac {1}{2}}AB\cdot CD\\[4pt]CD&={\tfrac {AC\cdot BC}{AB}}\\[4pt]\end{aligned}}$

History

The theorem that the three altitudes of a triangle concur (at the orthocenter) is not directly stated in survivingGreek mathematicaltexts, but is used in theBook of Lemmas(proposition 5), attributed toArchimedes(3rd century BC), citing the "commentary to the treatise about right-angled triangles", a work which does not survive. It was also mentioned byPappus(Mathematical Collection,VII, 62;c.340).The theorem was stated and proved explicitly byal-Nasawiin his (11th century) commentary on theBook of Lemmas,and attributed toal-Quhi(fl. 10th century).

This proof in Arabic was translated as part of the (early 17th century) Latin editions of theBook of Lemmas,but was not widely known in Europe, and the theorem was therefore proven several more times in the 17th–19th century.Samuel Maroloisproved it in hisGeometrie(1619), andIsaac Newtonproved it in an unfinished treatiseGeometry of Curved Lines(c.1680).LaterWilliam Chappleproved it in 1749.

A particularly elegant proof is due toFrançois-Joseph Servois(1804) and independentlyCarl Friedrich Gauss(1810): Draw a line parallel to each side of the triangle through the opposite point, and form a new triangle from the intersections of these three lines. Then the original triangle is themedial triangleof the new triangle, and the altitudes of the original triangle are theperpendicular bisectorsof the new triangle, and therefore concur (at the circumcenter of the new triangle).

See also

• Triangle center
• Median (geometry)

References

• Altshiller-Court, Nathan(2007) [1952],College Geometry,Dover
• Berele, Allan; Goldman, Jerry (2001),Geometry: Theorems and Constructions,Prentice Hall,ISBN0-13-087121-4
• Bogomolny, Alexander."Existence of the Orthocenter".Cut the Knot.Retrieved2022-12-17.
• Johnson, Roger A. (2007) [1960],Advanced Euclidean Geometry,Dover,ISBN978-0-486-46237-0
• Smart, James R. (1998),Modern Geometries(5th ed.), Brooks/Cole,ISBN0-534-35188-3

External links

• Weisstein, Eric W."Altitude".MathWorld.
• Orthocenter of a triangleWith interactive animation
• Animated demonstration of orthocenter constructionCompass and straightedge.
• Fagnano's Problemby Jay Warendorff,Wolfram Demonstrations Project.