Logarithm

Plots of logarithm functions, with three commonly used bases. The special pointslog_b b= 1are indicated by dotted lines, and all curves intersect inlog_b 1 = 0.

Inmathematics,thelogarithmtobasebis the inverse function ofexponentiationwith baseb.That means that the logarithm of a numberxto thebasebis theexponentto whichbmust be raised to producex.For example, since1000 = 10³,thelogarithm base$10$of1000is3,orlog₁₀ (1000) = 3.The logarithm ofxtobasebis denoted aslog_b (x),or without parentheses,log_b x.When the base is clear from the context or is irrelevant it is sometimes writtenlog x.

The logarithm base10is called thedecimalorcommonlogarithmand is commonly used in science and engineering. Thenaturallogarithmhas the numbere≈ 2.718as its base; its use is widespread in mathematics andphysicsbecause of its very simplederivative.Thebinarylogarithmuses base2and is frequently used incomputer science.

Logarithms were introduced byJohn Napierin 1614 as a means of simplifying calculations.They were rapidly adopted bynavigators,scientists, engineers,surveyors,and others to perform high-accuracy computations more easily. Usinglogarithm tables,tedious multi-digit multiplication steps can be replaced by table look-ups and simpler addition. This is possible because the logarithm of aproductis thesumof the logarithms of the factors: $$\log _{b}(xy)=\log _{b}x+\log _{b}y,$$ provided thatb,xandyare all positive andb≠ 1.Theslide rule,also based on logarithms, allows quick calculations without tables, but at lower precision. The present-day notion of logarithms comes fromLeonhard Euler,who connected them to theexponential functionin the 18th century, and who also introduced the lettereas the base of natural logarithms.

Logarithmic scalesreduce wide-ranging quantities to smaller scopes. For example, thedecibel(dB) is aunitused to expressratio as logarithms,mostly for signal power and amplitude (of whichsound pressureis a common example). In chemistry,pHis a logarithmic measure for theacidityof anaqueous solution.Logarithms are commonplace in scientificformulae,and in measurements of thecomplexity of algorithmsand of geometric objects calledfractals.They help to describefrequencyratios ofmusical intervals,appear in formulas countingprime numbersorapproximatingfactorials,inform some models inpsychophysics,and can aid inforensic accounting.

The concept of logarithm as the inverse of exponentiation extends to other mathematical structures as well. However, in general settings, the logarithm tends to be a multi-valued function. For example, thecomplex logarithmis the multi-valuedinverseof the complex exponential function. Similarly, thediscrete logarithmis the multi-valued inverse of the exponential function in finite groups; it has uses inpublic-key cryptography.

Motivation

Thegraphof the logarithm base 2 crosses thex-axisatx= 1and passes through the points(2, 1),(4, 2),and(8, 3),depicting, e.g.,log₂(8) = 3and2³= 8.The graph gets arbitrarily close to they-axis, butdoes not meet it.

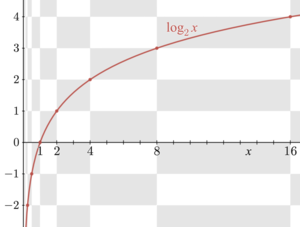
Addition,multiplication,andexponentiationare three of the most fundamental arithmetic operations. The inverse of addition issubtraction,and the inverse of multiplication isdivision.Similarly, a logarithm is the inverse operation ofexponentiation.Exponentiation is when a numberb,thebase,is raised to a certain powery,theexponent,to give a valuex;this is denoted $$b^{y}=x.$$ For example, raising2to the power of3gives8:$2^{3}=8.$

The logarithm of basebis the inverse operation, that provides the outputyfrom the inputx.That is,$y=\log _{b}x$is equivalent to$x=b^{y}$ifbis a positivereal number.(Ifbis not a positive real number, both exponentiation and logarithm can be defined but may take several values, which makes definitions much more complicated.)

One of the main historical motivations of introducing logarithms is the formula $$\log _{b}(xy)=\log _{b}x+\log _{b}y,$$ by whichtables of logarithmsallow multiplication and division to be reduced to addition and subtraction, a great aid to calculations before the invention of computers.

Definition

Given a positivereal numberbsuch thatb≠ 1,thelogarithmof a positive real numberxwith respect to basebis the exponent by whichbmust be raised to yieldx.In other words, the logarithm ofxto basebis the unique real numberysuch that$b^{y}=x$.

The logarithm is denoted "log_b x"(pronounced as" the logarithm ofxto baseb","thebase-blogarithm ofx",or most commonly" the log, baseb,ofx").

An equivalent and more succinct definition is that the functionlog_bis theinverse functionto the function$x\mapsto b^{x}$.

Examples

• log₂ 16 = 4,since2⁴= 2 × 2 × 2 × 2 = 16.
• Logarithms can also be negative:${\textstyle \log _{2}\!{\frac {1}{2}}=-1}$since${\textstyle 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.}$
• log₁₀ 150is approximately 2.176, which lies between 2 and 3, just as 150 lies between10²= 100and10³= 1000.
• For any baseb,log_b b= 1andlog_b 1 = 0,sinceb¹=bandb⁰= 1,respectively.

Logarithmic identities

Main article:List of logarithmic identities

Several important formulas, sometimes calledlogarithmic identitiesorlogarithmic laws,relate logarithms to one another.

Product, quotient, power, and root

The logarithm of a product is the sum of the logarithms of the numbers being multiplied; the logarithm of the ratio of two numbers is the difference of the logarithms. The logarithm of thep-th power of a number isptimes the logarithm of the number itself; the logarithm of ap-th root is the logarithm of the number divided byp.The following table lists these identities with examples. Each of the identities can be derived after substitution of the logarithm definitions$x=b^{\,\log _{b}x}$or$y=b^{\,\log _{b}y}$in the left hand sides.

Product, quotient, power, and root identities of logarithms

Identity	Formula	Example
Product	${\textstyle \log _{b}(xy)=\log _{b}x+\log _{b}y}$	${\textstyle \log _{3}243=\log _{3}(9\cdot 27)=\log _{3}9+\log _{3}27=2+3=5}$
Quotient	${\textstyle \log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y}$	${\textstyle \log _{2}16=\log _{2}\!{\frac {64}{4}}=\log _{2}64-\log _{2}4=6-2=4}$
Power	${\textstyle \log _{b}\left(x^{p}\right)=p\log _{b}x}$	${\textstyle \log _{2}64=\log _{2}\left(2^{6}\right)=6\log _{2}2=6}$
Root	${\textstyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}}$	${\textstyle \log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

Change of base

The logarithmlog_b xcan be computed from the logarithms ofxandbwith respect to an arbitrary basekusing the following formula: $$\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.$$

Typicalscientific calculatorscalculate the logarithms to bases 10 ande.Logarithms with respect to any basebcan be determined using either of these two logarithms by the previous formula: $$\log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.$$

Given a numberxand its logarithmy= log_b xto an unknown baseb,the base is given by:

$$b=x^{\frac {1}{y}},$$

which can be seen from taking the defining equation$x=b^{\,\log _{b}x}=b^{y}$to the power of${\tfrac {1}{y}}.$

Particular bases

Overlaid graphs of the logarithm for bases⁠ 1 /2⁠,2, ande

Among all choices for the base, three are particularly common. These areb= 10,b=e(theirrationalmathematical constante≈ 2.71828183),andb= 2(thebinary logarithm). Inmathematical analysis,the logarithm baseeis widespread because of analytical properties explained below. On the other hand,base 10logarithms (thecommon logarithm) are easy to use for manual calculations in thedecimalnumber system:

$$\log _{10}\,(\,10\,x\,)\ =\;\log _{10}10\ +\;\log _{10}x\ =\ 1\,+\,\log _{10}x\,.$$

Thus,log₁₀ (x)is related to the number ofdecimal digitsof a positive integerx:The number of digits is the smallestintegerstrictly bigger thanlog₁₀ (x). For example,log₁₀(5986)is approximately 3.78. Thenext integer aboveit is 4, which is the number of digits of 5986. Both the natural logarithm and the binary logarithm are used ininformation theory,corresponding to the use ofnatsorbitsas the fundamental units of information, respectively. Binary logarithms are also used incomputer science,where thebinary systemis ubiquitous; inmusic theory,where a pitch ratio of two (theoctave) is ubiquitous and the number ofcentsbetween any two pitches is a scaled version of the binary logarithm, or log 2 times 1200, of the pitch ratio (that is, 100 cents persemitoneinconventional equal temperament), or equivalently the log base2^1/1200;and inphotographyrescaled base 2 logarithms are used to measureexposure values,light levels,exposure times,lensapertures,andfilm speedsin "stops".

The abbreviationlog xis often used when the intended base can be inferred based on the context or discipline, or when the base is indeterminate or immaterial. Common logarithms (base 10), historically used in logarithm tables and slide rules, are a basic tool for measurement and computation in many areas of science and engineering; in these contextslog xstill often means the base ten logarithm.In mathematicslog xusually means to the natural logarithm (basee). In computer science and information theory,logoften refers to binary logarithms (base 2). The following table lists common notations for logarithms to these bases. The "ISO notation" column lists designations suggested by theInternational Organization for Standardization.

Baseb	Name for logb x	ISO notation	Other notations
2	binary logarithm	lbx	ldx,logx,lgx,log2 x
e	natural logarithm	lnx	logx,loge x
10	common logarithm	lgx	logx,log10 x
b	logarithm to baseb	logb x

History

Main article:History of logarithms

The history of logarithms in seventeenth-century Europe saw the discovery of a newfunctionthat extended the realm of analysis beyond the scope of algebraic methods. The method of logarithms was publicly propounded byJohn Napierin 1614, in a book titledMirifici Logarithmorum Canonis Descriptio(Description of the Wonderful Canon of Logarithms).Prior to Napier's invention, there had been other techniques of similar scopes, such as theprosthaphaeresisor the use of tables of progressions, extensively developed byJost Bürgiaround 1600.Napier coined the term for logarithm in Middle Latin,logarithmus,literally meaning'ratio-number',derived from the Greeklogos'proportion, ratio, word'+arithmos'number'.

Thecommon logarithmof a number is the index of that power of ten which equals the number.Speaking of a number as requiring so many figures is a rough allusion to common logarithm, and was referred to byArchimedesas the "order of a number".The first real logarithms were heuristic methods to turn multiplication into addition, thus facilitating rapid computation. Some of these methods used tables derived from trigonometric identities.Such methods are calledprosthaphaeresis.

Invention of thefunctionnow known as thenatural logarithmbegan as an attempt to perform aquadratureof a rectangularhyperbolabyGrégoire de Saint-Vincent,a Belgian Jesuit residing in Prague. Archimedes had writtenThe Quadrature of the Parabolain the third century BC, but a quadrature for the hyperbola eluded all efforts until Saint-Vincent published his results in 1647. The relation that the logarithm provides between ageometric progressionin itsargumentand anarithmetic progressionof values, promptedA. A. de Sarasato make the connection of Saint-Vincent's quadrature and the tradition of logarithms inprosthaphaeresis,leading to the term "hyperbolic logarithm", a synonym for natural logarithm. Soon the new function was appreciated byChristiaan Huygens,andJames Gregory.The notationLogywas adopted byLeibnizin 1675,and the next year he connected it to theintegral${\textstyle \int {\frac {dy}{y}}.}$

Before Euler developed his modern conception of complex natural logarithms,Roger Coteshad a nearly equivalent result when he showed in 1714 that $$\log(\cos \theta +i\sin \theta )=i\theta.$$

Logarithm tables, slide rules, and historical applications

The 1797Encyclopædia Britannicaexplanation of logarithms

By simplifying difficult calculations before calculators and computers became available, logarithms contributed to the advance of science, especiallyastronomy.They were critical to advances insurveying,celestial navigation,and other domains.Pierre-Simon Laplacecalled logarithms

"...[a]n admirable artifice which, by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations."

As the functionf(x) =b^xis the inverse function oflog_b x,it has been called anantilogarithm.Nowadays, this function is more commonly called anexponential function.

Log tables

A key tool that enabled the practical use of logarithms was thetable of logarithms.The first such table was compiled byHenry Briggsin 1617, immediately after Napier's invention but with the innovation of using 10 as the base. Briggs' first table contained thecommon logarithmsof all integers in the range from 1 to 1000, with a precision of 14 digits. Subsequently, tables with increasing scope were written. These tables listed the values oflog₁₀ xfor any numberxin a certain range, at a certain precision. Base-10 logarithms were universally used for computation, hence the name common logarithm, since numbers that differ by factors of 10 have logarithms that differ by integers. The common logarithm ofxcan be separated into aninteger partand afractional part,known as the characteristic andmantissa.Tables of logarithms need only include the mantissa, as the characteristic can be easily determined by counting digits from the decimal point.The characteristic of10 ·xis one plus the characteristic ofx,and their mantissas are the same. Thus using a three-digit log table, the logarithm of 3542 is approximated by

$${\begin{aligned}\log _{10}3542&=\log _{10}(1000\cdot 3.542)\\&=3+\log _{10}3.542\\&\approx 3+\log _{10}3.54\end{aligned}}$$

Greater accuracy can be obtained byinterpolation:

$$\log _{10}3542\approx {}3+\log _{10}3.54+0.2(\log _{10}3.55-\log _{10}3.54)$$

The value of10^xcan be determined by reverse look up in the same table, since the logarithm is amonotonic function.

Computations

The product and quotient of two positive numberscanddwere routinely calculated as the sum and difference of their logarithms. The productcdor quotientc/dcame from looking up the antilogarithm of the sum or difference, via the same table:

$$cd=10^{\,\log _{10}c}\,10^{\,\log _{10}d}=10^{\,\log _{10}c\,+\,\log _{10}d}$$ and $${\frac {c}{d}}=cd^{-1}=10^{\,\log _{10}c\,-\,\log _{10}d}.$$

For manual calculations that demand any appreciable precision, performing the lookups of the two logarithms, calculating their sum or difference, and looking up the antilogarithm is much faster than performing the multiplication by earlier methods such asprosthaphaeresis,which relies ontrigonometric identities.

Calculations of powers androotsare reduced to multiplications or divisions and lookups by $$c^{d}=\left(10^{\,\log _{10}c}\right)^{d}=10^{\,d\log _{10}c}$$

and $${\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.$$

Trigonometric calculations were facilitated by tables that contained the common logarithms oftrigonometric functions.

Slide rules

Another critical application was theslide rule,a pair of logarithmically divided scales used for calculation. The non-sliding logarithmic scale,Gunter's rule,was invented shortly after Napier's invention.William Oughtredenhanced it to create the slide rule—a pair of logarithmic scales movable with respect to each other. Numbers are placed on sliding scales at distances proportional to the differences between their logarithms. Sliding the upper scale appropriately amounts to mechanically adding logarithms, as illustrated here:

Schematic depiction of a slide rule. Starting from 2 on the lower scale, add the distance to 3 on the upper scale to reach the product 6. The slide rule works because it is marked such that the distance from 1 toxis proportional to the logarithm ofx.

For example, adding the distance from 1 to 2 on the lower scale to the distance from 1 to 3 on the upper scale yields a product of 6, which is read off at the lower part. The slide rule was an essential calculating tool for engineers and scientists until the 1970s, because it allows, at the expense of precision, much faster computation than techniques based on tables.

Analytic properties

A deeper study of logarithms requires the concept of afunction.A function is a rule that, given one number, produces another number.An example is the function producing thex-th power ofbfrom any real numberx,where the basebis a fixed number. This function is written asf(x) =b^x.Whenbis positive and unequal to 1, we show below thatfis invertible when considered as a function from the reals to the positive reals.

Existence

Letbbe a positive real number not equal to 1 and letf(x) =b^x.

It is a standard result in real analysis that any continuous strictly monotonic function is bijective between its domain and range. This fact follows from theintermediate value theorem.Now,fisstrictly increasing(forb> 1), or strictly decreasing (for0 <b< 1),is continuous, has domain$\mathbb {R}$,and has range$\mathbb {R} _{>0}$.Therefore,fis a bijection from$\mathbb {R}$to$\mathbb {R} _{>0}$.In other words, for each positive real numbery,there is exactly one real numberxsuch that$b^{x}=y$.

We let$\log _{b}\colon \mathbb {R} _{>0}\to \mathbb {R}$denote the inverse off.That is,log_b yis the unique real numberxsuch that$b^{x}=y$.This function is called the base-blogarithm functionorlogarithmic function(or justlogarithm).

Characterization by the product formula

The functionlog_b xcan also be essentially characterized by the product formula $$\log _{b}(xy)=\log _{b}x+\log _{b}y.$$ More precisely, the logarithm to any baseb> 1is the onlyincreasing functionffrom the positive reals to the reals satisfyingf(b) = 1and$$f(xy)=f(x)+f(y).$$

Graph of the logarithm function

The graph of the logarithm functionlog_b (x)(blue) is obtained byreflectingthe graph of the functionb^x(red) at the diagonal line (x=y).

As discussed above, the functionlog_bis the inverse to the exponential function$x\mapsto b^{x}$.Therefore, theirgraphscorrespond to each other upon exchanging thex- and they-coordinates (or upon reflection at the diagonal linex=y), as shown at the right: a point(t,u=b^t)on the graph offyields a point(u,t= log_b u)on the graph of the logarithm and vice versa. As a consequence,log_b (x)diverges to infinity(gets bigger than any given number) ifxgrows to infinity, provided thatbis greater than one. In that case,log_b(x)is anincreasing function.Forb< 1,log_b (x)tends to minus infinity instead. Whenxapproaches zero,log_b xgoes to minus infinity forb> 1(plus infinity forb< 1,respectively).

Derivative and antiderivative

The graph of thenatural logarithm(green) and its tangent atx= 1.5(black)

Analytic properties of functions pass to their inverses.Thus, asf(x) =b^xis a continuous anddifferentiable function,so islog_b y.Roughly, a continuous function is differentiable if its graph has no sharp "corners". Moreover, as thederivativeoff(x)evaluates toln(b)b^xby the properties of theexponential function,thechain ruleimplies that the derivative oflog_b xis given by $${\frac {d}{dx}}\log _{b}x={\frac {1}{x\ln b}}.$$ That is, theslopeof thetangenttouching the graph of thebase-blogarithm at the point(x,log_b (x))equals1/(x ln(b)).

The derivative ofln(x)is1/x;this implies thatln(x)is the uniqueantiderivativeof1/xthat has the value 0 forx= 1.It is this very simple formula that motivated to qualify as "natural" the natural logarithm; this is also one of the main reasons of the importance of theconstante.

The derivative with a generalized functional argumentf(x)is $${\frac {d}{dx}}\ln f(x)={\frac {f'(x)}{f(x)}}.$$ The quotient at the right hand side is called thelogarithmic derivativeoff.Computingf'(x)by means of the derivative ofln(f(x))is known aslogarithmic differentiation.The antiderivative of thenatural logarithmln(x)is: $$\int \ln(x)\,dx=x\ln(x)-x+C.$$ Related formulas,such as antiderivatives of logarithms to other bases can be derived from this equation using the change of bases.

Integral representation of the natural logarithm

Thenatural logarithmoftis the shaded area underneath the graph of the functionf(x) = 1/x(reciprocal ofx).

Thenatural logarithmoftcan be defined as thedefinite integral:

$$\ln t=\int _{1}^{t}{\frac {1}{x}}\,dx.$$ This definition has the advantage that it does not rely on the exponential function or any trigonometric functions; the definition is in terms of an integral of a simple reciprocal. As an integral,ln(t)equals the area between thex-axis and the graph of the function1/x,ranging fromx= 1tox=t.This is a consequence of thefundamental theorem of calculusand the fact that the derivative ofln(x)is1/x.Product and power logarithm formulas can be derived from this definition.For example, the product formulaln(tu) = ln(t) + ln(u)is deduced as:

$${\begin{aligned}\ln(tu)&=\int _{1}^{tu}{\frac {1}{x}}\,dx\\&{\stackrel {(1)}{=}}\int _{1}^{t}{\frac {1}{x}}\,dx+\int _{t}^{tu}{\frac {1}{x}}\,dx\\&{\stackrel {(2)}{=}}\ln(t)+\int _{1}^{u}{\frac {1}{w}}\,dw\\&=\ln(t)+\ln(u).\end{aligned}}$$

The equality (1) splits the integral into two parts, while the equality (2) is a change of variable (w=x/t). In the illustration below, the splitting corresponds to dividing the area into the yellow and blue parts. Rescaling the left hand blue area vertically by the factortand shrinking it by the same factor horizontally does not change its size. Moving it appropriately, the area fits the graph of the functionf(x) = 1/xagain. Therefore, the left hand blue area, which is the integral off(x)fromttotuis the same as the integral from 1 tou.This justifies the equality (2) with a more geometric proof.

A visual proof of the product formula of the natural logarithm

The power formulaln(t^r) =rln(t)may be derived in a similar way:

$${\begin{aligned}\ln(t^{r})&=\int _{1}^{t^{r}}{\frac {1}{x}}dx\\&=\int _{1}^{t}{\frac {1}{w^{r}}}\left(rw^{r-1}\,dw\right)\\&=r\int _{1}^{t}{\frac {1}{w}}\,dw\\&=r\ln(t).\end{aligned}}$$ The second equality uses a change of variables (integration by substitution),w=x^1/r.

The sum over the reciprocals of natural numbers, $$1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},$$ is called theharmonic series.It is closely tied to thenatural logarithm:asntends toinfinity,the difference, $$\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),$$ converges(i.e. gets arbitrarily close) to a number known as theEuler–Mascheroni constantγ= 0.5772....This relation aids in analyzing the performance of algorithms such asquicksort.

Transcendence of the logarithm

Real numbersthat are notalgebraicare calledtranscendental;for example,πandeare such numbers, but${\sqrt {2-{\sqrt {3}}}}$is not.Almost allreal numbers are transcendental. The logarithm is an example of atranscendental function.TheGelfond–Schneider theoremasserts that logarithms usually take transcendental, i.e. "difficult" values.

Calculation

The logarithm keys (LOG for base 10 and LN for basee) on aTI-83 Plusgraphing calculator

Logarithms are easy to compute in some cases, such aslog₁₀ (1000) = 3.In general, logarithms can be calculated usingpower seriesor thearithmetic–geometric mean,or be retrieved from a precalculatedlogarithm tablethat provides a fixed precision.Newton's method,an iterative method to solve equations approximately, can also be used to calculate the logarithm, because its inverse function, the exponential function, can be computed efficiently.Using look-up tables,CORDIC-like methods can be used to compute logarithms by using only the operations of addition andbit shifts.Moreover, thebinary logarithm algorithmcalculateslb(x)recursively,based on repeated squarings ofx,taking advantage of the relation $$\log _{2}\left(x^{2}\right)=2\log _{2}|x|.$$

Power series

Taylor series

The Taylor series ofln(z)centered atz= 1.The animation shows the first 10 approximations along with the 99th and 100th. The approximations do not converge beyond a distance of 1 from the center.

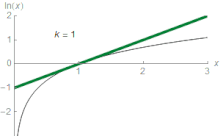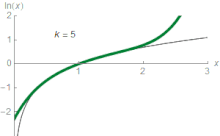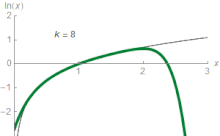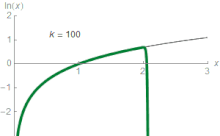
For any real numberzthat satisfies0 <z≤ 2,the following formula holds:

$${\begin{aligned}\ln(z)&={\frac {(z-1)^{1}}{1}}-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}}-{\frac {(z-1)^{4}}{4}}+\cdots \\&=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {(z-1)^{k}}{k}}.\end{aligned}}$$

Equating the functionln(z)to this infinite sum (series) is shorthand for saying that the function can be approximated to a more and more accurate value by the following expressions (known aspartial sums):

$$(z-1),\ \ (z-1)-{\frac {(z-1)^{2}}{2}},\ \ (z-1)-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}},\ \ldots$$

For example, withz= 1.5the third approximation yields0.4167,which is about0.011greater thanln(1.5) = 0.405465,and the ninth approximation yields0.40553,which is only about0.0001greater. Thenth partial sum can approximateln(z)with arbitrary precision, provided the number of summandsnis large enough.

In elementary calculus, the series is said toconvergeto the functionln(z),and the function is thelimitof the series. It is theTaylor seriesof thenatural logarithmatz= 1.The Taylor series ofln(z)provides a particularly useful approximation toln(1 +z)whenzis small,|z| < 1,since then $$\ln(1+z)=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}-\cdots \approx z.$$

For example, withz= 0.1the first-order approximation givesln(1.1) ≈ 0.1,which is less than5%off the correct value0.0953.

Inverse hyperbolic tangent

Another series is based on theinverse hyperbolic tangentfunction: $$\ln(z)=2\cdot \operatorname {artanh} \,{\frac {z-1}{z+1}}=2\left({\frac {z-1}{z+1}}+{\frac {1}{3}}{\left({\frac {z-1}{z+1}}\right)}^{3}+{\frac {1}{5}}{\left({\frac {z-1}{z+1}}\right)}^{5}+\cdots \right),$$ for any real numberz> 0.Usingsigma notation,this is also written as $$\ln(z)=2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {z-1}{z+1}}\right)^{2k+1}.$$ This series can be derived from the above Taylor series. It converges quicker than the Taylor series, especially ifzis close to 1. For example, forz= 1.5,the first three terms of the second series approximateln(1.5)with an error of about3×10⁻⁶.The quick convergence forzclose to 1 can be taken advantage of in the following way: given a low-accuracy approximationy≈ ln(z)and putting $$A={\frac {z}{\exp(y)}},$$ the logarithm ofzis: $$\ln(z)=y+\ln(A).$$ The better the initial approximationyis, the closerAis to 1, so its logarithm can be calculated efficiently.Acan be calculated using theexponential series,which converges quickly providedyis not too large. Calculating the logarithm of largerzcan be reduced to smaller values ofzby writingz=a· 10^b,so thatln(z) = ln(a) +b· ln(10).

A closely related method can be used to compute the logarithm of integers. Putting$\textstyle z={\frac {n+1}{n}}$in the above series, it follows that: $$\ln(n+1)=\ln(n)+2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {1}{2n+1}}\right)^{2k+1}.$$ If the logarithm of a large integernis known, then this series yields a fast converging series forlog(n+1),with arate of convergenceof${\textstyle \left({\frac {1}{2n+1}}\right)^{2}}$.

Arithmetic–geometric mean approximation

Thearithmetic–geometric meanyields high-precision approximations of thenatural logarithm.Sasaki and Kanada showed in 1982 that it was particularly fast for precisions between 400 and 1000 decimal places, while Taylor series methods were typically faster when less precision was needed. In their workln(x)is approximated to a precision of2^−p(orpprecise bits) by the following formula (due toCarl Friedrich Gauss):

$$\ln(x)\approx {\frac {\pi }{2\,\mathrm {M} \!\left(1,2^{2-m}/x\right)}}-m\ln(2).$$

HereM(x,y)denotes thearithmetic–geometric meanofxandy.It is obtained by repeatedly calculating the average(x+y)/2(arithmetic mean) and${\textstyle {\sqrt {xy}}}$(geometric mean) ofxandythen let those two numbers become the nextxandy.The two numbers quickly converge to a common limit which is the value ofM(x,y).mis chosen such that

$$x\,2^{m}>2^{p/2}.\,$$

to ensure the required precision. A largermmakes theM(x,y)calculation take more steps (the initialxandyare farther apart so it takes more steps to converge) but gives more precision. The constantsπandln(2)can be calculated with quickly converging series.

Feynman's algorithm

While atLos Alamos National Laboratoryworking on theManhattan Project,Richard Feynmandeveloped a bit-processing algorithm to compute the logarithm that is similar to long division and was later used in theConnection Machine.The algorithm relies on the fact that every real numberxwhere1 <x< 2can be represented as a product of distinct factors of the form1 + 2^−k.The algorithm sequentially builds that productP,starting withP= 1andk= 1:ifP· (1 + 2^−k) <x,then it changesPtoP· (1 + 2^−k).It then increases$k$by one regardless. The algorithm stops whenkis large enough to give the desired accuracy. Becauselog(x)is the sum of the terms of the formlog(1 + 2^−k)corresponding to thosekfor which the factor1 + 2^−kwas included in the productP,log(x)may be computed by simple addition, using a table oflog(1 + 2^−k)for allk.Any base may be used for the logarithm table.

Applications

Anautilusshell displaying a logarithmic spiral

Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion ofscale invariance.For example, each chamber of the shell of anautilusis an approximate copy of the next one, scaled by a constant factor. This gives rise to alogarithmic spiral.Benford's lawon the distribution of leading digits can also be explained by scale invariance.Logarithms are also linked toself-similarity.For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions.The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms.Logarithmic scalesare useful for quantifying the relative change of a value as opposed to its absolute difference. Moreover, because the logarithmic functionlog(x)grows very slowly for largex,logarithmic scales are used to compress large-scale scientific data. Logarithms also occur in numerous scientific formulas, such as theTsiolkovsky rocket equation,theFenske equation,or theNernst equation.

Logarithmic scale

Main article:Logarithmic scale

A logarithmic chart depicting the value of oneGoldmarkinPapiermarksduring theGerman hyperinflation in the 1920s

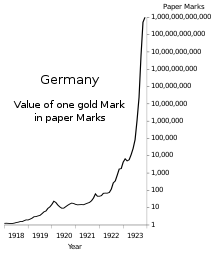
Scientific quantities are often expressed as logarithms of other quantities, using alogarithmic scale.For example, thedecibelis aunit of measurementassociated withlogarithmic-scalequantities.It is based on the common logarithm ofratios—10 times the common logarithm of apowerratio or 20 times the common logarithm of avoltageratio. It is used to quantify the attenuation or amplification of electrical signals,to describe power levels of sounds inacoustics,and theabsorbanceof light in the fields ofspectrometryandoptics.Thesignal-to-noise ratiodescribing the amount of unwantednoisein relation to a (meaningful)signalis also measured in decibels.In a similar vein, thepeak signal-to-noise ratiois commonly used to assess the quality of sound andimage compressionmethods using the logarithm.

The strength of an earthquake is measured by taking the common logarithm of the energy emitted at the quake. This is used in themoment magnitude scaleor theRichter magnitude scale.For example, a 5.0 earthquake releases 32 times(10^1.5)and a 6.0 releases 1000 times(10³)the energy of a 4.0.Apparent magnitudemeasures the brightness of stars logarithmically.Inchemistrythe negative of the decimal logarithm, the decimalcologarithm,is indicated by the letter p.For instance,pHis the decimal cologarithm of theactivityofhydroniumions (the formhydrogenionsH⁺
take in water).The activity of hydronium ions in neutral water is 10⁻⁷mol·L⁻¹,hence a pH of 7. Vinegar typically has a pH of about 3. The difference of 4 corresponds to a ratio of 10⁴of the activity, that is, vinegar's hydronium ion activity is about10⁻³mol·L⁻¹.

Semilog(log–linear) graphs use the logarithmic scale concept for visualization: one axis, typically the vertical one, is scaled logarithmically. For example, the chart at the right compresses the steep increase from 1 million to 1 trillion to the same space (on the vertical axis) as the increase from 1 to 1 million. In such graphs,exponential functionsof the formf(x) =a·b^xappear as straight lines withslopeequal to the logarithm ofb.Log-loggraphs scale both axes logarithmically, which causes functions of the formf(x) =a·x^kto be depicted as straight lines with slope equal to the exponentk.This is applied in visualizing and analyzingpower laws.

Psychology

Logarithms occur in several laws describinghuman perception:Hick's lawproposes a logarithmic relation between the time individuals take to choose an alternative and the number of choices they have.Fitts's lawpredicts that the time required to rapidly move to a target area is a logarithmic function of the ratio between the distance to a target and the size of the target.Inpsychophysics,theWeber–Fechner lawproposes a logarithmic relationship betweenstimulusandsensationsuch as the actual vs. the perceived weight of an item a person is carrying.(This "law", however, is less realistic than more recent models, such asStevens's power law.)

Psychological studies found that individuals with little mathematics education tend to estimate quantities logarithmically, that is, they position a number on an unmarked line according to its logarithm, so that 10 is positioned as close to 100 as 100 is to 1000. Increasing education shifts this to a linear estimate (positioning 1000 10 times as far away) in some circumstances, while logarithms are used when the numbers to be plotted are difficult to plot linearly.

Probability theory and statistics

Threeprobability density functions(PDF) of random variables with log-normal distributions. The location parameterμ,which is zero for all three of the PDFs shown, is the mean of the logarithm of the random variable, not the mean of the variable itself.

Distribution of first digits (in %, red bars) in thepopulation of the 237 countriesof the world. Black dots indicate the distribution predicted by Benford's law.

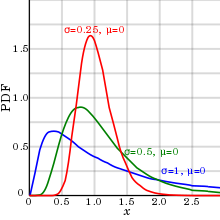
Logarithms arise inprobability theory:thelaw of large numbersdictates that, for afair coin,as the number of coin-tosses increases to infinity, the observed proportion of headsapproaches one-half.The fluctuations of this proportion about one-half are described by thelaw of the iterated logarithm.

Logarithms also occur inlog-normal distributions.When the logarithm of arandom variablehas anormal distribution,the variable is said to have a log-normal distribution.Log-normal distributions are encountered in many fields, wherever a variable is formed as the product of many independent positive random variables, for example in the study of turbulence.

Logarithms are used formaximum-likelihood estimationof parametricstatistical models.For such a model, thelikelihood functiondepends on at least oneparameterthat must be estimated. A maximum of the likelihood function occurs at the same parameter-value as a maximum of the logarithm of the likelihood (the "log likelihood"), because the logarithm is an increasing function. The log-likelihood is easier to maximize, especially for the multiplied likelihoods forindependentrandom variables.

Benford's lawdescribes the occurrence of digits in manydata sets,such as heights of buildings. According to Benford's law, the probability that the first decimal-digit of an item in the data sample isd(from 1 to 9) equalslog₁₀ (d+ 1) − log₁₀ (d),regardlessof the unit of measurement.Thus, about 30% of the data can be expected to have 1 as first digit, 18% start with 2, etc. Auditors examine deviations from Benford's law to detect fraudulent accounting.

Thelogarithm transformationis a type ofdata transformationused to bring the empirical distribution closer to the assumed one.

Computational complexity

Analysis of algorithmsis a branch ofcomputer sciencethat studies theperformanceofalgorithms(computer programs solving a certain problem).Logarithms are valuable for describing algorithms thatdivide a probleminto smaller ones, and join the solutions of the subproblems.

For example, to find a number in a sorted list, thebinary search algorithmchecks the middle entry and proceeds with the half before or after the middle entry if the number is still not found. This algorithm requires, on average,log₂ (N)comparisons, whereNis the list's length.Similarly, themerge sortalgorithm sorts an unsorted list by dividing the list into halves and sorting these first before merging the results. Merge sort algorithms typically require a timeapproximately proportional toN· log(N).The base of the logarithm is not specified here, because the result only changes by a constant factor when another base is used. A constant factor is usually disregarded in the analysis of algorithms under the standarduniform cost model.

A functionf(x)is said togrow logarithmicallyiff(x)is (exactly or approximately) proportional to the logarithm ofx.(Biological descriptions of organism growth, however, use this term for an exponential function.) For example, anynatural numberNcan be represented inbinary formin no more thanlog₂ N+ 1bits.In other words, the amount ofmemoryneeded to storeNgrows logarithmically withN.

Entropy and chaos

Billiardson an ovalbilliard table.Two particles, starting at the center with an angle differing by one degree, take paths that diverge chaotically because ofreflectionsat the boundary.

Entropyis broadly a measure of the disorder of some system. Instatistical thermodynamics,the entropySof some physical system is defined as $$S=-k\sum _{i}p_{i}\ln(p_{i}).\,$$ The sum is over all possible statesiof the system in question, such as the positions of gas particles in a container. Moreover,p_iis the probability that the stateiis attained andkis theBoltzmann constant.Similarly,entropy in information theorymeasures the quantity of information. If a message recipient may expect any one ofNpossible messages with equal likelihood, then the amount of information conveyed by any one such message is quantified aslog₂ Nbits.

Lyapunov exponentsuse logarithms to gauge the degree of chaoticity of adynamical system.For example, for a particle moving on an oval billiard table, even small changes of the initial conditions result in very different paths of the particle. Such systems arechaoticin adeterministicway, because small measurement errors of the initial state predictably lead to largely different final states.At least one Lyapunov exponent of a deterministically chaotic system is positive.

Fractals

The Sierpinski triangle (at the right) is constructed by repeatedly replacingequilateral trianglesby three smaller ones.

Logarithms occur in definitions of thedimensionoffractals.Fractals are geometric objects that are self-similar in the sense that small parts reproduce, at least roughly, the entire global structure. TheSierpinski triangle(pictured) can be covered by three copies of itself, each having sides half the original length. This makes theHausdorff dimensionof this structureln(3)/ln(2) ≈ 1.58.Another logarithm-based notion of dimension is obtained bycounting the number of boxesneeded to cover the fractal in question.

Music

Four different octaves shown on a linear scale, then shown on a logarithmic scale (as the ear hears them)

Logarithms are related to musical tones andintervals.Inequal temperamenttunings, the frequency ratio depends only on the interval between two tones, not on the specific frequency, orpitch,of the individual tones. In the12-tone equal temperamenttuning common in modern Western music, eachoctave(doubling of frequency) is broken into twelve equally spaced intervals calledsemitones.For example, if thenoteAhas a frequency of 440Hzthen the noteB-flathas a frequency of 466 Hz. The interval betweenAandB-flatis asemitone,as is the one betweenB-flatandB(frequency 493 Hz). Accordingly, the frequency ratios agree: $${\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.$$

Intervals between arbitrary pitches can be measured in octaves by taking thebase-2logarithm of thefrequencyratio, can be measured in equally tempered semitones by taking thebase-2^1/12logarithm (12times thebase-2logarithm), or can be measured incents,hundredths of a semitone, by taking thebase-2^1/1200logarithm (1200times thebase-2logarithm). The latter is used for finer encoding, as it is needed for finer measurements or non-equal temperaments.

Interval (the two tones are played at the same time)	1/12 tone	Semitone	Just major third	Major third	Tritone	Octave
Frequency ratio $r$	$2^{\frac {1}{72}}\approx 1.0097$	$2^{\frac {1}{12}}\approx 1.0595$	${\tfrac {5}{4}}=1.25$	${\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}$	${\begin{aligned}2^{\frac {6}{12}}&={\sqrt {2}}\\&\approx 1.4142\end{aligned}}$	$2^{\frac {12}{12}}=2$
Number of semitones $12\log _{2}r$	${\tfrac {1}{6}}$	$1$	$\approx 3.8631$	$4$	$6$	$12$
Number of cents $1200\log _{2}r$	$16{\tfrac {2}{3}}$	$100$	$\approx 386.31$	$400$	$600$	$1200$

Number theory

Natural logarithmsare closely linked tocounting prime numbers(2, 3, 5, 7, 11,...), an important topic innumber theory.For anyintegerx,the quantity ofprime numbersless than or equal toxis denotedπ(x).Theprime number theoremasserts thatπ(x)is approximately given by $${\frac {x}{\ln(x)}},$$ in the sense that the ratio ofπ(x)and that fraction approaches 1 whenxtends to infinity.As a consequence, the probability that a randomly chosen number between 1 andxis prime is inverselyproportionalto the number of decimal digits ofx.A far better estimate ofπ(x)is given by theoffset logarithmic integralfunctionLi(x),defined by $$\mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln(t)}}\,dt.$$ TheRiemann hypothesis,one of the oldest open mathematicalconjectures,can be stated in terms of comparingπ(x)andLi(x).TheErdős–Kac theoremdescribing the number of distinctprime factorsalso involves thenatural logarithm.

The logarithm ofnfactorial,n!= 1 · 2 ·... ·n,is given by $$\ln(n!)=\ln(1)+\ln(2)+\cdots +\ln(n).$$ This can be used to obtainStirling's formula,an approximation ofn!for largen.

Generalizations

Complex logarithm

Main article:Complex logarithm

Polar form ofz = x + iy.Bothφandφ'are arguments ofz.

All thecomplex numbersathat solve the equation

$$e^{a}=z$$

are calledcomplex logarithmsofz,whenzis (considered as) a complex number. A complex number is commonly represented asz = x + iy,wherexandyare real numbers andiis animaginary unit,the square of which is −1. Such a number can be visualized by a point in thecomplex plane,as shown at the right. Thepolar formencodes a non-zero complex numberzby itsabsolute value,that is, the (positive, real) distancerto theorigin,and an angle between the real (x) axisReand the line passing through both the origin andz.This angle is called theargumentofz.

The absolute valuerofzis given by

$$\textstyle r={\sqrt {x^{2}+y^{2}}}.$$

Using the geometrical interpretation ofsineandcosineand their periodicity in2π,any complex numberzmay be denoted as

$${\begin{aligned}z&=x+iy\\&=r(\cos \varphi +i\sin \varphi )\\&=r(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )),\end{aligned}}$$

for any integer numberk.Evidently the argument ofzis not uniquely specified: bothφandφ'=φ+ 2kπare valid arguments ofzfor all integersk,because adding2kπradiansork⋅360°toφcorresponds to "winding" around the origin counter-clock-wise bykturns.The resulting complex number is alwaysz,as illustrated at the right fork= 1.One may select exactly one of the possible arguments ofzas the so-calledprincipal argument,denotedArg(z),with a capitalA,by requiringφto belong to one, conveniently selected turn, e.g.−π<φ≤πor0 ≤φ< 2π.These regions, where the argument ofzis uniquely determined are calledbranchesof the argument function.

The principal branch (-π,π) of the complex logarithm,Log(z).The black point atz= 1corresponds to absolute value zero and brighter colors refer to bigger absolute values. Thehueof the color encodes the argument ofLog(z).

Euler's formulaconnects thetrigonometric functionssineandcosineto thecomplex exponential: $$e^{i\varphi }=\cos \varphi +i\sin \varphi.$$

Using this formula, and again the periodicity, the following identities hold:

$${\begin{aligned}z&=r\left(\cos \varphi +i\sin \varphi \right)\\&=r\left(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )\right)\\&=re^{i(\varphi +2k\pi )}\\&=e^{\ln(r)}e^{i(\varphi +2k\pi )}\\&=e^{\ln(r)+i(\varphi +2k\pi )}=e^{a_{k}},\end{aligned}}$$

whereln(r)is the unique real natural logarithm,a_kdenote the complex logarithms ofz,andkis an arbitrary integer. Therefore, the complex logarithms ofz,which are all those complex valuesa_kfor which thea_k-thpower ofeequalsz,are the infinitely many values $$a_{k}=\ln(r)+i(\varphi +2k\pi ),$$ for arbitrary integersk.

Takingksuch thatφ+ 2kπis within the defined interval for the principal arguments, thena_kis called theprincipal valueof the logarithm, denotedLog(z),again with a capitalL.The principal argument of any positive real numberxis 0; henceLog(x)is a real number and equals the real (natural) logarithm. However, the above formulas for logarithms of products and powersdonotgeneralizeto the principal value of the complex logarithm.

The illustration at the right depictsLog(z),confining the arguments ofzto the interval(−π, π].This way the corresponding branch of the complex logarithm has discontinuities all along the negative realxaxis, which can be seen in the jump in the hue there. This discontinuity arises from jumping to the other boundary in the same branch, when crossing a boundary, i.e. not changing to the correspondingk-value of the continuously neighboring branch. Such a locus is called abranch cut.Dropping the range restrictions on the argument makes the relations "argument ofz",and consequently the" logarithm ofz",multi-valued functions.

Inverses of other exponential functions

Exponentiation occurs in many areas of mathematics and its inverse function is often referred to as the logarithm. For example, thelogarithm of a matrixis the (multi-valued) inverse function of thematrix exponential.Another example is thep-adic logarithm,the inverse function of thep-adic exponential.Both are defined via Taylor series analogous to the real case.In the context ofdifferential geometry,theexponential mapmaps thetangent spaceat a point of amanifoldto aneighborhoodof that point. Its inverse is also called the logarithmic (or log) map.

In the context offinite groupsexponentiation is given by repeatedly multiplying one group elementbwith itself. Thediscrete logarithmis the integernsolving the equation $$b^{n}=x,$$ wherexis an element of the group. Carrying out the exponentiation can be done efficiently, but the discrete logarithm is believed to be very hard to calculate in some groups. This asymmetry has important applications inpublic key cryptography,such as for example in theDiffie–Hellman key exchange,a routine that allows secure exchanges ofcryptographickeys over unsecured information channels.Zech's logarithmis related to the discrete logarithm in the multiplicative group of non-zero elements of afinite field.

Further logarithm-like inverse functions include thedouble logarithmln(ln(x)),thesuper- or hyper-4-logarithm(a slight variation of which is callediterated logarithmin computer science), theLambert W function,and thelogit.They are the inverse functions of thedouble exponential function,tetration,off(w) =we^w,and of thelogistic function,respectively.

Related concepts

From the perspective ofgroup theory,the identitylog(cd) = log(c) + log(d)expresses agroup isomorphismbetween positiverealsunder multiplication and reals under addition. Logarithmic functions are the only continuous isomorphisms between these groups.By means of that isomorphism, theHaar measure(Lebesgue measure)dxon the reals corresponds to the Haar measuredx/xon the positive reals.The non-negative reals not only have a multiplication, but also have addition, and form asemiring,called theprobability semiring;this is in fact asemifield.The logarithm then takes multiplication to addition (log multiplication), and takes addition to log addition (LogSumExp), giving anisomorphismof semirings between the probability semiring and thelog semiring.

Logarithmic one-formsdf/fappear incomplex analysisandalgebraic geometryasdifferential formswith logarithmicpoles.

Thepolylogarithmis the function defined by $$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}.$$ It is related to thenatural logarithmbyLi₁ (z) = −ln(1 −z).Moreover,Li_s (1)equals theRiemann zeta functionζ(s).

See also

• Decimal exponent(dex)
• Exponential function
• Index of logarithm articles

External links

• Media related toLogarithmat Wikimedia Commons
• The dictionary definition oflogarithmat Wiktionary
• Quotations related toHistory of logarithmsat Wikiquote
• A lesson on logarithms can be found on Wikiversity
• Weisstein, Eric W.,"Logarithm",MathWorld
• Khan Academy: Logarithms, free online micro lectures
• "Logarithmic function",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Colin Byfleet,Educational video on logarithms,retrieved12 October2010
• Edward Wright,Translation of Napier's work on logarithms,archived fromthe originalon 3 December 2002,retrieved12 October2010
• Glaisher, James Whitbread Lee (1911),"Logarithm",inChisholm, Hugh(ed.),Encyclopædia Britannica,vol. 16 (11th ed.), Cambridge University Press, pp. 868–77