BigOnotation

Example of Big O notation:${\color {red}f(x)}=O{\color {blue}(g(x))}$as$x\to \infty$since there exists$M>0$(e.g.,$M=1$) and$x_{0}$(e.g.,$x_{0}=5$) such that$0\leq {\color {red}f(x)}\leq M{\color {blue}g(x)}$whenever$x\geq x_{0}$.

BigOnotationis a mathematical notation that describes thelimiting behaviorof afunctionwhen theargumenttends towards a particular value or infinity. Big O is a member of afamily of notationsinvented by German mathematiciansPaul Bachmann,Edmund Landau,and others, collectively calledBachmann–Landau notationorasymptotic notation.The letter O was chosen by Bachmann to stand forOrdnung,meaning theorder of approximation.

Incomputer science,big O notation is used toclassify algorithmsaccording to how their run time or space requirements grow as the input size grows.Inanalytic number theory,big O notation is often used to express a bound on the difference between anarithmetical functionand a better understood approximation; a famous example of such a difference is the remainder term in theprime number theorem.Big O notation is also used in many other fields to provide similar estimates.

Big O notation characterizes functions according to their growth rates: different functions with the same asymptotic growth rate may be represented using the same O notation. The letter O is used because the growth rate of a function is also referred to as theorder of the function.A description of a function in terms of big O notation usually only provides anupper boundon the growth rate of the function.

Associated with big O notation are several related notations, using the symbolso,Ω,ω,andΘ,to describe other kinds of bounds on asymptotic growth rates.

Formal definition

Let$f$,the function to be estimated, be arealorcomplexvalued function, and let$g$,the comparison function, be a real valued function. Let both functions be defined on someunboundedsubsetof the positivereal numbers,and$g(x)$be strictly positive for all large enough values of$x$.One writes $$f(x)=O{\bigl (}g(x){\bigr )}\quad {\text{ as }}x\to \infty$$ and it is read "$f(x)$is big O of$g(x)$"if theabsolute valueof$f(x)$is at most a positive constant multiple of$g(x)$for all sufficiently large values of$x$.That is,$f(x)=O{\bigl (}g(x){\bigr )}$if there exists a positive real number$M$and a real number$x_{0}$such that $$|f(x)|\leq Mg(x)\quad {\text{ for all }}x\geq x_{0}.$$ In many contexts, the assumption that we are interested in the growth rate as the variable$x$goes to infinity is left unstated, and one writes more simply that $$f(x)=O{\bigl (}g(x){\bigr )}.$$ The notation can also be used to describe the behavior of$f$near some real number$a$(often,$a=0$): we say $$f(x)=O{\bigl (}g(x){\bigr )}\quad {\text{ as }}x\to a$$ if there exist positive numbers$\delta$and$M$such that for all defined$x$with$0<|x-a|<\delta$, $$|f(x)|\leq Mg(x).$$ As$g(x)$is chosen to be strictly positive for such values of$x$,both of these definitions can be unified using thelimit superior: $$f(x)=O{\bigl (}g(x){\bigr )}\quad {\text{ as }}x\to a$$ if $$\limsup _{x\to a}{\frac {\left|f(x)\right|}{g(x)}}<\infty.$$ And in both of these definitions thelimit point$a$(whether$\infty$or not) is acluster pointof the domains of$f$and$g$,i. e., in every neighbourhood of$a$there have to be infinitely many points in common. Moreover, as pointed out in the article about thelimit inferior and limit superior,the$\textstyle \limsup _{x\to a}$(at least on theextended real number line) always exists.

In computer science, a slightly more restrictive definition is common:$f$and$g$are both required to be functions from some unbounded subset of thepositive integersto the nonnegative real numbers; then$f(x)=O{\bigl (}g(x){\bigr )}$if there exist positive integer numbers$M$and$n_{0}$such that$f(n)\leq Mg(n)$for all$n\geq n_{0}$.

Example

In typical usage theOnotation is asymptotical, that is, it refers to very largex.In this setting, the contribution of the terms that grow "most quickly" will eventually make the other ones irrelevant. As a result, the following simplification rules can be applied:

• Iff(x)is a sum of several terms, if there is one with largest growth rate, it can be kept, and all others omitted.
• Iff(x)is a product of several factors, any constants (factors in the product that do not depend onx) can be omitted.

For example, letf(x) = 6x⁴− 2x³+ 5,and suppose we wish to simplify this function, usingOnotation, to describe its growth rate asxapproaches infinity. This function is the sum of three terms:6x⁴,−2x³,and5.Of these three terms, the one with the highest growth rate is the one with the largest exponent as a function ofx,namely6x⁴.Now one may apply the second rule:6x⁴is a product of6andx⁴in which the first factor does not depend onx.Omitting this factor results in the simplified formx⁴.Thus, we say thatf(x)is a "big O" ofx⁴.Mathematically, we can writef(x) =O(x⁴).One may confirm this calculation using the formal definition: letf(x) = 6x⁴− 2x³+ 5andg(x) =x⁴.Applying theformal definitionfrom above, the statement thatf(x) =O(x⁴)is equivalent to its expansion, $$|f(x)|\leq Mx^{4}$$ for some suitable choice of a real numberx₀and a positive real numberMand for allx>x₀.To prove this, letx₀= 1andM= 13.Then, for allx>x₀: $${\begin{aligned}|6x^{4}-2x^{3}+5|&\leq 6x^{4}+|2x^{3}|+5\\&\leq 6x^{4}+2x^{4}+5x^{4}\\&=13x^{4}\end{aligned}}$$ so $$|6x^{4}-2x^{3}+5|\leq 13x^{4}.$$

Usage

Big O notation has two main areas of application:

• Inmathematics,it is commonly used to describehow closely a finite series approximates a given function,especially in the case of a truncatedTaylor seriesorasymptotic expansion
• Incomputer science,it is useful in theanalysis of algorithms

In both applications, the functiong(x)appearing within theO(·)is typically chosen to be as simple as possible, omitting constant factors and lower order terms.

There are two formally close, but noticeably different, usages of this notation:

• infiniteasymptotics
• infinitesimalasymptotics.

This distinction is only in application and not in principle, however—the formal definition for the "big O" is the same for both cases, only with different limits for the function argument.

Infinite asymptotics

Graphs of functions commonly used in the analysis of algorithms, showing the number of operationsNversus input sizenfor each function

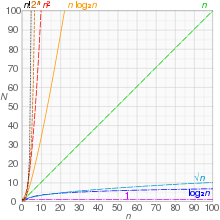
Big O notation is useful whenanalyzing algorithmsfor efficiency. For example, the time (or the number of steps) it takes to complete a problem of sizenmight be found to beT(n) = 4n²− 2n+ 2.Asngrows large, then²termwill come to dominate, so that all other terms can be neglected—for instance whenn= 500,the term4n²is 1000 times as large as the2nterm. Ignoring the latter would have negligible effect on the expression's value for most purposes. Further, thecoefficientsbecome irrelevant if we compare to any otherorderof expression, such as an expression containing a termn³orn⁴.Even ifT(n) = 1,000,000n²,ifU(n) =n³,the latter will always exceed the former oncengrows larger than1,000,000,viz.T(1,000,000) = 1,000,000³=U(1,000,000).Additionally, the number of steps depends on the details of the machine model on which the algorithm runs, but different types of machines typically vary by only a constant factor in the number of steps needed to execute an algorithm. So the big O notation captures what remains: we write either

$T(n)=O(n^{2})$

or

$T(n)\in O(n^{2})$

and say that the algorithm hasorder ofn²time complexity. The sign "="is not meant to express" is equal to "in its normal mathematical sense, but rather a more colloquial" is ", so the second expression is sometimes considered more accurate (see the"Equals sign"discussion below) while the first is considered by some as anabuse of notation.

Infinitesimal asymptotics

Big O can also be used to describe theerror termin an approximation to a mathematical function. The most significant terms are written explicitly, and then the least-significant terms are summarized in a single big O term. Consider, for example, theexponential seriesand two expressions of it that are valid whenxis small:

${\begin{aligned}e^{x}&=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\dotsb &{\text{for all }}x\\[4pt]&=1+x+{\frac {x^{2}}{2}}+O(x^{3})&{\text{as }}x\to 0\\[4pt]&=1+x+O(x^{2})&{\text{as }}x\to 0\end{aligned}}$

The middle expression (the one withO(x³)) means the absolute-value of the errore^x− (1 +x+x²/2) is at most some constant times |x³| whenxis close enough to 0.

Properties

If the functionfcan be written as a finite sum of other functions, then the fastest growing one determines the order off(n).For example,

$f(n)=9\log n+5(\log n)^{4}+3n^{2}+2n^{3}=O(n^{3})\qquad {\text{as }}n\to \infty.$

In particular, if a function may be bounded by a polynomial inn,then asntends toinfinity,one may disregardlower-orderterms of the polynomial. The setsO(n^c)andO(cⁿ)are very different. Ifcis greater than one, then the latter grows much faster. A function that grows faster thann^cfor anycis calledsuperpolynomial.One that grows more slowly than any exponential function of the formcⁿis calledsubexponential.An algorithm can require time that is both superpolynomial and subexponential; examples of this include the fastest known algorithms forinteger factorizationand the functionn^logn.

We may ignore any powers ofninside of the logarithms. The setO(logn)is exactly the same asO(log(n^c)).The logarithms differ only by a constant factor (sincelog(n^c) =clogn) and thus the big O notation ignores that. Similarly, logs with different constant bases are equivalent. On the other hand, exponentials with different bases are not of the same order. For example,2ⁿand3ⁿare not of the same order.

Changing units may or may not affect the order of the resulting algorithm. Changing units is equivalent to multiplying the appropriate variable by a constant wherever it appears. For example, if an algorithm runs in the order ofn²,replacingnbycnmeans the algorithm runs in the order ofc²n²,and the big O notation ignores the constantc².This can be written asc²n²= O(n²).If, however, an algorithm runs in the order of2ⁿ,replacingnwithcngives2^cn= (2^c)ⁿ.This is not equivalent to2ⁿin general. Changing variables may also affect the order of the resulting algorithm. For example, if an algorithm's run time isO(n)when measured in terms of the numbernofdigitsof an input numberx,then its run time isO(logx)when measured as a function of the input numberxitself, becausen=O(logx).

Product

$f_{1}=O(g_{1}){\text{ and }}f_{2}=O(g_{2})\Rightarrow f_{1}f_{2}=O(g_{1}g_{2})$

$f\cdot O(g)=O(fg)$

Sum

If$f_{1}=O(g_{1})$and$f_{2}=O(g_{2})$then$f_{1}+f_{2}=O(\max(g_{1},g_{2}))$.It follows that if$f_{1}=O(g)$and$f_{2}=O(g)$then$f_{1}+f_{2}\in O(g)$.In other words, this second statement says that$O(g)$is aconvex cone.

Multiplication by a constant

Letkbe a nonzero constant. Then$O(|k|\cdot g)=O(g)$.In other words, if$f=O(g)$,then$k\cdot f=O(g).$

Multiple variables

BigO(and little o, Ω, etc.) can also be used with multiple variables. To define bigOformally for multiple variables, suppose$f$and$g$are two functions defined on some subset of$\mathbb {R} ^{n}$.We say

$f(\mathbf {x} ){\text{ is }}O(g(\mathbf {x} ))\quad {\text{ as }}\mathbf {x} \to \infty$

if and only if there exist constants$M$and$C>0$such that$|f(\mathbf {x} )|\leq C|g(\mathbf {x} )|$for all$\mathbf {x}$with$x_{i}\geq M$for some$i.$ Equivalently, the condition that$x_{i}\geq M$for some$i$can be written$\|\mathbf {x} \|_{\infty }\geq M$,where$\|\mathbf {x} \|_{\infty }$denotes theChebyshev norm.For example, the statement

$f(n,m)=n^{2}+m^{3}+O(n+m)\quad {\text{ as }}n,m\to \infty$

asserts that there exist constantsCandMsuch that

$|f(n,m)-(n^{2}+m^{3})|\leq C|n+m|$

whenever either$m\geq M$or$n\geq M$holds. This definition allows all of the coordinates of$\mathbf {x}$to increase to infinity. In particular, the statement

$f(n,m)=O(n^{m})\quad {\text{ as }}n,m\to \infty$

(i.e.,$\exists C\,\exists M\,\forall n\,\forall m\,\cdots$) is quite different from

$\forall m\colon ~f(n,m)=O(n^{m})\quad {\text{ as }}n\to \infty$

(i.e.,$\forall m\,\exists C\,\exists M\,\forall n\,\cdots$).

Under this definition, the subset on which a function is defined is significant when generalizing statements from the univariate setting to the multivariate setting. For example, if$f(n,m)=1$and$g(n,m)=n$,then$f(n,m)=O(g(n,m))$if we restrict$f$and$g$to$[1,\infty )^{2}$,but not if they are defined on$[0,\infty )^{2}$.

This is not the only generalization of big O to multivariate functions, and in practice, there is some inconsistency in the choice of definition.

Matters of notation

Equals sign

The statement "f(x) isO(g(x)) "as defined above is usually written asf(x) =O(g(x)).Some consider this to be anabuse of notation,since the use of the equals sign could be misleading as it suggests a symmetry that this statement does not have. Asde Bruijnsays,O(x) =O(x²)is true butO(x²) =O(x)is not.Knuthdescribes such statements as "one-way equalities", since if the sides could be reversed, "we could deduce ridiculous things liken=n²from the identitiesn=O(n²)andn²=O(n²)."In another letter, Knuth also pointed out that "the equality sign is not symmetric with respect to such notations", as, in this notation, "mathematicians customarily use the = sign as they use the word" is "in English: Aristotle is a man, but a man isn't necessarily Aristotle".

For these reasons, it would be more precise to useset notationand writef(x) ∈O(g(x))(read as: "f(x)is an element ofO(g(x)) ", or"f(x) is in the setO(g(x)) "), thinking ofO(g(x)) as the class of all functionsh(x) such that|h(x)| ≤Cg(x)for some positive real numberC.However, the use of the equals sign is customary.

Other arithmetic operators

Big O notation can also be used in conjunction with other arithmetic operators in more complicated equations. For example,h(x) +O(f(x))denotes the collection of functions having the growth ofh(x) plus a part whose growth is limited to that off(x). Thus,

$g(x)=h(x)+O(f(x))$

expresses the same as

$g(x)-h(x)=O(f(x)).$

Example

Suppose analgorithmis being developed to operate on a set ofnelements. Its developers are interested in finding a functionT(n) that will express how long the algorithm will take to run (in some arbitrary measurement of time) in terms of the number of elements in the input set. The algorithm works by first calling a subroutine to sort the elements in the set and then perform its own operations. The sort has a known time complexity ofO(n²), and after the subroutine runs the algorithm must take an additional55n³+ 2n+ 10steps before it terminates. Thus the overall time complexity of the algorithm can be expressed asT(n) = 55n³+O(n²).Here the terms2n+ 10are subsumed within the faster-growingO(n²). Again, this usage disregards some of the formal meaning of the "=" symbol, but it does allow one to use the big O notation as a kind of convenient placeholder.

Multiple uses

In more complicated usage,O(·) can appear in different places in an equation, even several times on each side. For example, the following are true for$n\to \infty$: $${\begin{aligned}(n+1)^{2}&=n^{2}+O(n),\\(n+O(n^{1/2}))\cdot (n+O(\log n))^{2}&=n^{3}+O(n^{5/2}),\\n^{O(1)}&=O(e^{n}).\end{aligned}}$$ The meaning of such statements is as follows: foranyfunctions which satisfy eachO(·) on the left side, there aresomefunctions satisfying eachO(·) on the right side, such that substituting all these functions into the equation makes the two sides equal. For example, the third equation above means: "For any functionf(n) =O(1), there is some functiong(n) =O(eⁿ) such thatn^f(n)=g(n). "In terms of the" set notation "above, the meaning is that the class of functions represented by the left side is a subset of the class of functions represented by the right side. In this use the" = "is a formal symbol that unlike the usual use of" = "is not asymmetric relation.Thus for examplen^O(1)=O(eⁿ)does not imply the false statementO(eⁿ) =n^O(1).

Typesetting

Big O is typeset as an italicized uppercase "O", as in the following example:$O(n^{2})$.InTeX,it is produced by simply typing O inside math mode. Unlike Greek-named Bachmann–Landau notations, it needs no special symbol. However, some authors use the calligraphic variant${\mathcal {O}}$instead.

Orders of common functions

Further information:Time complexity § Table of common time complexities

Here is a list of classes of functions that are commonly encountered when analyzing the running time of an algorithm. In each case,cis a positive constant andnincreases without bound. The slower-growing functions are generally listed first.

Notation	Name	Example
$O(1)$	constant	Finding the median value for a sorted array of numbers; Calculating$(-1)^{n}$;Using a constant-sizelookup table
$O(\alpha (n))$	inverse Ackermann function	Amortized complexity per operation for theDisjoint-set data structure
$O(\log \log n)$	double logarithmic	Average number of comparisons spent finding an item usinginterpolation searchin a sorted array of uniformly distributed values
$O(\log n)$	logarithmic	Finding an item in a sorted array with abinary searchor a balanced searchtreeas well as all operations in abinomial heap
$O((\log n)^{c})$ ${\textstyle c>1}$	polylogarithmic	Matrix chain ordering can be solved in polylogarithmic time on aparallel random-access machine.
$O(n^{c})$ ${\textstyle 0<c<1}$	fractional power	Searching in ak-d tree
$O(n)$	linear	Finding an item in an unsorted list or in an unsorted array; adding twon-bit integers byripple carry
$O(n\log ^{*}n)$	nlog-starn	Performingtriangulationof a simple polygon usingSeidel's algorithm,where$\log ^{*}(n)={\begin{cases}0,&{\text{if }}n\leq 1\\1+\log ^{*}(\log n),&{\text{if }}n>1\end{cases}}$
$O(n\log n)=O(\log n!)$	linearithmic,loglinear, quasilinear, or "nlogn"	Performing afast Fourier transform;fastest possiblecomparison sort;heapsortandmerge sort
$O(n^{2})$	quadratic	Multiplying twon-digit numbers byschoolbook multiplication;simple sorting algorithms, such asbubble sort,selection sortandinsertion sort;(worst-case) bound on some usually faster sorting algorithms such asquicksort,Shellsort,andtree sort
$O(n^{c})$	polynomialor algebraic	Tree-adjoining grammarparsing; maximummatchingforbipartite graphs;finding thedeterminantwithLU decomposition
$L_{n}[\alpha,c]=e^{(c+o(1))(\ln n)^{\alpha }(\ln \ln n)^{1-\alpha }}$ ${\textstyle 0<\alpha <1}$	L-notationorsub-exponential	Factoring a number using thequadratic sieveornumber field sieve
$O(c^{n})$ ${\textstyle c>1}$	exponential	Finding the (exact) solution to thetravelling salesman problemusingdynamic programming;determining if two logical statements are equivalent usingbrute-force search
$O(n!)$	factorial	Solving thetravelling salesman problemvia brute-force search; generating all unrestricted permutations of aposet;finding thedeterminantwithLaplace expansion;enumeratingall partitions of a set

The statement$f(n)=O(n!)$is sometimes weakened to$f(n)=O\left(n^{n}\right)$to derive simpler formulas for asymptotic complexity. For any$k>0$and$c>0$,$O(n^{c}(\log n)^{k})$is a subset of$O(n^{c+\varepsilon })$for any$\varepsilon >0$,so may be considered as a polynomial with some bigger order.

Related asymptotic notations

BigOis widely used in computer science. Together with some other related notations, it forms the family of Bachmann–Landau notations.

Little-o notation

"Little o" redirects here. For the baseball player, seeOmar Vizquel.

Intuitively, the assertion "f(x)iso(g(x))"(read"f(x)is little-o ofg(x)") means thatg(x)grows much faster thanf(x),or equivalentlyf(x)grows much slower thang(x).As before, letfbe a real or complex valued function andga real valued function, both defined on some unbounded subset of the positivereal numbers,such thatg(x) is strictly positive for all large enough values ofx.One writes

$f(x)=o(g(x))\quad {\text{ as }}x\to \infty$

if for every positive constantεthere exists a constant$x_{0}$such that

$|f(x)|\leq \varepsilon g(x)\quad {\text{ for all }}x\geq x_{0}.$

For example, one has

$2x=o(x^{2})$and$1/x=o(1),$both as$x\to \infty.$

The difference between thedefinition of the big-O notationand the definition of little-o is that while the former has to be true forat least oneconstantM,the latter must hold foreverypositive constantε,however small.In this way, little-o notation makes astronger statementthan the corresponding big-O notation: every function that is little-o ofgis also big-O ofg,but not every function that is big-O ofgis little-o ofg.For example,$2x^{2}=O(x^{2})$but$2x^{2}\neq o(x^{2})$.

Ifg(x) is nonzero, or at least becomes nonzero beyond a certain point, the relation$f(x)=o(g(x))$is equivalent to

$\lim _{x\to \infty }{\frac {f(x)}{g(x)}}=0$(and this is in fact how Landauoriginally defined the little-o notation).

Little-o respects a number of arithmetic operations. For example,

ifcis a nonzero constant and$f=o(g)$then$c\cdot f=o(g)$,and

if$f=o(F)$and$g=o(G)$then$f\cdot g=o(F\cdot G).$

It also satisfies atransitivityrelation:

if$f=o(g)$and$g=o(h)$then$f=o(h).$

Big Omega notation

Another asymptotic notation is$\Omega$,read "big omega".There are two widespread and incompatible definitions of the statement

$f(x)=\Omega (g(x))$as$x\to a$,

whereais some real number,$\infty$,or$-\infty$,wherefandgare real functions defined in a neighbourhood ofa,and wheregis positive in this neighbourhood.

The Hardy–Littlewood definition is used mainly inanalytic number theory,and the Knuth definition mainly incomputational complexity theory;the definitions are not equivalent.

The Hardy–Littlewood definition

In 1914Godfrey Harold HardyandJohn Edensor Littlewoodintroduced the new symbol$\Omega$,which is defined as follows:

$f(x)=\Omega (g(x))$as$x\to \infty$if$\limsup _{x\to \infty }\left|{\frac {f(x)}{g(x)}}\right|>0.$

Thus$f(x)=\Omega (g(x))$is the negation of$f(x)=o(g(x))$.

In 1916 the same authors introduced the two new symbols$\Omega _{R}$and$\Omega _{L}$,defined as:

$f(x)=\Omega _{R}(g(x))$as$x\to \infty$if$\limsup _{x\to \infty }{\frac {f(x)}{g(x)}}>0$;

$f(x)=\Omega _{L}(g(x))$as$x\to \infty$if$\liminf _{x\to \infty }{\frac {f(x)}{g(x)}}<0.$

These symbols were used byEdmund Landau,with the same meanings, in 1924.After Landau, the notations were never used again exactly thus;$\Omega _{R}$became$\Omega _{+}$and$\Omega _{L}$became$\Omega _{-}$.

These three symbols$\Omega,\Omega _{+},\Omega _{-}$,as well as$f(x)=\Omega _{\pm }(g(x))$(meaning that$f(x)=\Omega _{+}(g(x))$and$f(x)=\Omega _{-}(g(x))$are both satisfied), are now currently used inanalytic number theory.

Simple examples

We have

$\sin x=\Omega (1)$as$x\to \infty,$

and more precisely

$\sin x=\Omega _{\pm }(1)$as$x\to \infty.$

We have

$\sin x+1=\Omega (1)$as$x\to \infty,$

and more precisely

$\sin x+1=\Omega _{+}(1)$as$x\to \infty;$

however

$\sin x+1\not =\Omega _{-}(1)$as$x\to \infty.$

The Knuth definition

In 1976Donald Knuthpublished a paper to justify his use of the$\Omega$-symbol to describe a stronger property.Knuth wrote: "For all the applications I have seen so far in computer science, a stronger requirement... is much more appropriate". He defined

$f(x)=\Omega (g(x))\Leftrightarrow g(x)=O(f(x))$

with the comment: "Although I have changed Hardy and Littlewood's definition of$\Omega$,I feel justified in doing so because their definition is by no means in wide use, and because there are other ways to say what they want to say in the comparatively rare cases when their definition applies. "

Family of Bachmann–Landau notations

Notation	Name	Description	Formal definition	Limit definition
$f(n)=o(g(n))$	Small O; Small Oh; Little O; Little Oh	fis dominated bygasymptotically (for any constant factor$k$)	$\forall k>0\,\exists n_{0}\,\forall n>n_{0}\colon |f(n)|\leq k\,g(n)$	$\lim _{n\to \infty }{\frac {f(n)}{g(n)}}=0$
$f(n)=O(g(n))$	Big O; Big Oh; Big Omicron	$|f|$is asymptotically bounded above byg(up to constant factor$k$)	$\exists k>0\,\exists n_{0}\,\forall n>n_{0}\colon |f(n)|\leq k\,g(n)$	$\limsup _{n\to \infty }{\frac {f(n)}{g(n)}}<\infty$
$f(n)\asymp g(n)$(Hardy's notation) or$f(n)=\Theta (g(n))$(Knuth notation)	Of the same order as (Hardy); Big Theta (Knuth)	fis asymptotically bounded bygboth above (with constant factor$k_{2}$) and below (with constant factor$k_{1}$)	$\exists k_{1}>0\,\exists k_{2}>0\,\exists n_{0}\,\forall n>n_{0}\colon$$k_{1}\,g(n)\leq f(n)\leq k_{2}\,g(n)$	$f(n)=O(g(n))$and$g(n)=O(f(n))$
$f(n)\sim g(n)$	Asymptotic equivalence	fis equal togasymptotically	$\forall \varepsilon >0\,\exists n_{0}\,\forall n>n_{0}\colon \left|{\frac {f(n)}{g(n)}}-1\right|<\varepsilon$	$\lim _{n\to \infty }{\frac {f(n)}{g(n)}}=1$
$f(n)=\Omega (g(n))$	Big Omega in complexity theory (Knuth)	fis bounded below bygasymptotically	$\exists k>0\,\exists n_{0}\,\forall n>n_{0}\colon f(n)\geq k\,g(n)$	$\liminf _{n\to \infty }{\frac {f(n)}{g(n)}}>0$
$f(n)=\omega (g(n))$	Small Omega; Little Omega	fdominatesgasymptotically	$\forall k>0\,\exists n_{0}\,\forall n>n_{0}\colon f(n)>k\,g(n)$	$\lim _{n\to \infty }{\frac {f(n)}{g(n)}}=\infty$
$f(n)=\Omega (g(n))$	Big Omega in number theory (Hardy–Littlewood)	$|f|$is not dominated bygasymptotically	$\exists k>0\,\forall n_{0}\,\exists n>n_{0}\colon |f(n)|\geq k\,g(n)$	$\limsup _{n\to \infty }{\frac {\left|f(n)\right|}{g(n)}}>0$

The limit definitions assume$g(n)>0$for sufficiently large$n$.The table is (partly) sorted from smallest to largest, in the sense that$o,O,\Theta,\sim,$(Knuth's version of)$\Omega,\omega$on functions correspond to$<,\leq,\approx,=,$$\geq,>$on the real line(the Hardy–Littlewood version of$\Omega$,however, doesn't correspond to any such description).

Computer science uses the big$O$,big Theta$\Theta$,little$o$,little omega$\omega$and Knuth's big Omega$\Omega$notations.Analytic number theory often uses the big$O$,small$o$,Hardy's$\asymp$,Hardy–Littlewood's big Omega$\Omega$(with or without the +, − or ± subscripts) and$\sim$notations.The small omega$\omega$notation is not used as often in analysis.

Use in computer science

Further information:Analysis of algorithms

Informally, especially in computer science, the bigOnotation often can be used somewhat differently to describe an asymptotictightbound where using big Theta Θ notation might be more factually appropriate in a given context.For example, when considering a functionT(n) = 73n³+ 22n²+ 58, all of the following are generally acceptable, but tighter bounds (such as numbers 2 and 3 below) are usually strongly preferred over looser bounds (such as number 1 below).

1. T(n) =O(n¹⁰⁰)
2. T(n) =O(n³)
3. T(n) = Θ(n³)

The equivalent English statements are respectively:

1. T(n) grows asymptotically no faster thann¹⁰⁰
2. T(n) grows asymptotically no faster thann³
3. T(n) grows asymptotically as fast asn³.

So while all three statements are true, progressively more information is contained in each. In some fields, however, the big O notation (number 2 in the lists above) would be used more commonly than the big Theta notation (items numbered 3 in the lists above). For example, ifT(n) represents the running time of a newly developed algorithm for input sizen,the inventors and users of the algorithm might be more inclined to put an upper asymptotic bound on how long it will take to run without making an explicit statement about the lower asymptotic bound.

Other notation

In their bookIntroduction to Algorithms,Cormen,Leiserson,RivestandSteinconsider the set of functionsfwhich satisfy

$f(n)=O(g(n))\quad (n\to \infty )~.$

In a correct notation this set can, for instance, be calledO(g), where

$$O(g)=\{f:{\text{there exist positive constants}}~c~{\text{and}}~n_{0}~{\text{such that}}~0\leq f(n)\leq cg(n){\text{ for all }}n\geq n_{0}\}.$$

The authors state that the use of equality operator (=) to denote set membership rather than the set membership operator (∈) is an abuse of notation, but that doing so has advantages.Inside an equation or inequality, the use of asymptotic notation stands for an anonymous function in the setO(g), which eliminates lower-order terms, and helps to reduce inessential clutter in equations, for example:

$2n^{2}+3n+1=2n^{2}+O(n).$

Extensions to the Bachmann–Landau notations

Another notation sometimes used in computer science isÕ(readsoft-O), which hides polylogarithmic factors. There are two definitions in use: some authors usef(n) =Õ(g(n)) asshorthandforf(n) =O(g(n)log^kn)for somek,while others use it as shorthand forf(n) =O(g(n) log^kg(n)).Wheng(n)is polynomial inn,there is no difference; however, the latter definition allows one to say, e.g. that$n2^{n}={\tilde {O}}(2^{n})$while the former definition allows for$\log ^{k}n={\tilde {O}}(1)$for any constantk.Some authors writeO^*for the same purpose as the latter definition.Essentially, it is bigOnotation, ignoringlogarithmic factorsbecause thegrowth-rateeffects of some other super-logarithmic function indicate a growth-rate explosion for large-sized input parameters that is more important to predicting bad run-time performance than the finer-point effects contributed by the logarithmic-growth factor(s). This notation is often used to obviate the "nitpicking" within growth-rates that are stated as too tightly bounded for the matters at hand (since log^knis alwayso(n^ε) for any constantkand anyε> 0).

Also, theLnotation,defined as

$L_{n}[\alpha,c]=e^{(c+o(1))(\ln n)^{\alpha }(\ln \ln n)^{1-\alpha }},$

is convenient for functions that are betweenpolynomialandexponentialin terms of$\ln n$.

Generalizations and related usages

The generalization to functions taking values in anynormed vector spaceis straightforward (replacing absolute values by norms), wherefandgneed not take their values in the same space. A generalization to functionsgtaking values in anytopological groupis also possible. The "limiting process"x→x_ocan also be generalized by introducing an arbitraryfilter base,i.e. to directednetsfandg.Theonotation can be used to definederivativesanddifferentiabilityin quite general spaces, and also (asymptotical) equivalence of functions,

$f\sim g\iff (f-g)\in o(g)$

which is anequivalence relationand a more restrictive notion than the relationship "fis Θ(g) "from above. (It reduces to limf/g= 1 iffandgare positive real valued functions.) For example, 2xis Θ(x), but2x−xis noto(x).

History (Bachmann–Landau, Hardy, and Vinogradov notations)

The symbol O was first introduced by number theoristPaul Bachmannin 1894, in the second volume of his bookAnalytische Zahlentheorie( "analytic number theory").The number theoristEdmund Landauadopted it, and was thus inspired to introduce in 1909 the notation o;hence both are now called Landau symbols. These notations were used in applied mathematics during the 1950s for asymptotic analysis. The symbol$\Omega$(in the sense "is not anoof ") was introduced in 1914 by Hardy and Littlewood.Hardy and Littlewood also introduced in 1916 the symbols$\Omega _{R}$( "right" ) and$\Omega _{L}$( "left" ),precursors of the modern symbols$\Omega _{+}$( "is not smaller than a small o of" ) and$\Omega _{-}$( "is not larger than a small o of" ). Thus the Omega symbols (with their original meanings) are sometimes also referred to as "Landau symbols". This notation$\Omega$became commonly used in number theory at least since the 1950s.

The symbol$\sim$,although it had been used before with different meanings,was given its modern definition by Landau in 1909and by Hardy in 1910.Just above on the same page of his tract Hardy defined the symbol$\asymp$,where$f(x)\asymp g(x)$means that both$f(x)=O(g(x))$and$g(x)=O(f(x))$are satisfied. The notation is still currently used in analytic number theory.In his tract Hardy also proposed the symbol$\,\asymp \!\!\!\!\!\!-$,where$f\asymp \!\!\!\!\!\!-g$means that$f\sim Kg$for some constant$K\not =0$.

In the 1970s the big O was popularized in computer science byDonald Knuth,who proposed the different notation$f(x)=\Theta (g(x))$for Hardy's$f(x)\asymp g(x)$,and proposed a different definition for the Hardy and Littlewood Omega notation.

Two other symbols coined by Hardy were (in terms of the modernOnotation)

$f\preccurlyeq g\iff f=O(g)$and$f\prec g\iff f=o(g);$

(Hardy however never defined or used the notation$\prec \!\!\prec$,nor$\ll$,as it has been sometimes reported). Hardy introduced the symbols$\preccurlyeq$and$\prec$(as well as the already mentioned other symbols) in his 1910 tract "Orders of Infinity", and made use of them only in three papers (1910–1913). In his nearly 400 remaining papers and books he consistently used the Landau symbols O and o.

Hardy's symbols$\preccurlyeq$and$\prec$(as well as$\,\asymp \!\!\!\!\!\!-$) are not used anymore. On the other hand, in the 1930s,the Russian number theoristIvan Matveyevich Vinogradovintroduced his notation$\ll$,which has been increasingly used in number theory instead of the$O$notation. We have

$f\ll g\iff f=O(g),$

and frequently both notations are used in the same paper.

The big-O originally stands for "order of" ( "Ordnung", Bachmann 1894), and is thus a Latin letter. Neither Bachmann nor Landau ever call it "Omicron". The symbol was much later on (1976) viewed by Knuth as a capitalomicron,probably in reference to his definition of the symbolOmega.The digitzeroshould not be used.

See also

• Asymptotic computational complexity
• Asymptotic expansion:Approximation of functions generalizing Taylor's formula
• Asymptotically optimal algorithm:A phrase frequently used to describe an algorithm that has an upper bound asymptotically within a constant of a lower bound for the problem
• Big O in probability notation:O_p,o_p
• Limit inferior and limit superior:An explanation of some of the limit notation used in this article
• Master theorem (analysis of algorithms):For analyzing divide-and-conquer recursive algorithms using Big O notation
• Nachbin's theorem:A precise method of boundingcomplex analyticfunctions so that the domain of convergence ofintegral transformscan be stated
• Order of approximation
• Computational complexity of mathematical operations

Further reading

• Hardy, G. H.(1910).Orders of Infinity: The 'Infinitärcalcül' of Paul du Bois-Reymond.Cambridge University Press.
• Knuth, Donald(1997). "1.2.11: Asymptotic Representations".Fundamental Algorithms.The Art of Computer Programming. Vol. 1 (3rd ed.). Addison-Wesley.ISBN978-0-201-89683-1.
• Cormen, Thomas H.;Leiserson, Charles E.;Rivest, Ronald L.;Stein, Clifford(2001). "3.1: Asymptotic notation".Introduction to Algorithms(2nd ed.). MIT Press and McGraw-Hill.ISBN978-0-262-03293-3.
• Sipser, Michael(1997).Introduction to the Theory of Computation.PWS Publishing. pp.226–228.ISBN978-0-534-94728-6.
• Avigad, Jeremy; Donnelly, Kevin (2004).Formalizing O notation in Isabelle/HOL(PDF).International Joint Conference on Automated Reasoning.doi:10.1007/978-3-540-25984-8_27.
• Black, Paul E. (11 March 2005). Black, Paul E. (ed.)."big-O notation".Dictionary of Algorithms and Data Structures.U.S. National Institute of Standards and Technology.RetrievedDecember 16,2006.
• Black, Paul E. (17 December 2004). Black, Paul E. (ed.)."little-o notation".Dictionary of Algorithms and Data Structures.U.S. National Institute of Standards and Technology.RetrievedDecember 16,2006.
• Black, Paul E. (17 December 2004). Black, Paul E. (ed.)."Ω".Dictionary of Algorithms and Data Structures.U.S. National Institute of Standards and Technology.RetrievedDecember 16,2006.
• Black, Paul E. (17 December 2004). Black, Paul E. (ed.)."ω".Dictionary of Algorithms and Data Structures.U.S. National Institute of Standards and Technology.RetrievedDecember 16,2006.
• Black, Paul E. (17 December 2004). Black, Paul E. (ed.)."Θ".Dictionary of Algorithms and Data Structures.U.S. National Institute of Standards and Technology.RetrievedDecember 16,2006.

External links

• Growth of sequences — OEIS (Online Encyclopedia of Integer Sequences) Wiki
• Introduction to Asymptotic Notations
• Big-O Notation – What is it good for
• An example of Big O in accuracy of central divided difference scheme for first derivativeArchived2018-10-07 at theWayback Machine
• A Gentle Introduction to Algorithm Complexity Analysis