Bode plot

Figure 1A:High-pass filter(1st-order, one-pole) Bode magnitude plot (top) and Bode phase plot (bottom). The red data curve is approximated by the straight black line.

Figure 1B:Low-pass filter(1st-order, one-pole) Bode magnitude plot (top) and Bode phase plot (bottom). The red data curve is approximated by the straight black line.

Inelectrical engineeringandcontrol theory,aBode plot/ˈboʊdi/is agraphof thefrequency responseof a system. It is usually a combination of aBode magnitude plot,expressing the magnitude (usually indecibels) of the frequency response, and aBode phase plot,expressing thephase shift.

As originally conceived byHendrik Wade Bodein the 1930s, the plot is anasymptoticapproximationof the frequency response,using straight line segments.

Overview

Among his several important contributions tocircuit theoryandcontrol theory,engineerHendrik Wade Bode,while working atBell Labsin the 1930s, devised a simple but accurate method for graphinggainand phase-shift plots. These bear his name,Bode gain plotandBode phase plot."Bode" is often pronounced/ˈboʊdi/BOH-dee,although the Dutch pronunciation isDutch:[ˈboːdə]BOH-duh.

Bode was faced with the problem of designing stableamplifierswithfeedbackfor use in telephone networks. He developed the graphical design technique of the Bode plots to show thegain marginandphase marginrequired to maintain stability under variations in circuit characteristics caused during manufacture or during operation.The principles developed were applied to design problems ofservomechanismsand other feedback control systems. The Bode plot is an example of analysis in thefrequency domain.

Definition

The Bode plot for alinear, time-invariantsystem withtransfer function$H(s)$($s$being the complex frequency in theLaplace domain) consists of a magnitude plot and a phase plot.

TheBode magnitude plotis the graph of the function$|H(s=j\omega )|$of frequency$\omega$(with$j$being theimaginary unit). The$\omega$-axis of the magnitude plot is logarithmic and the magnitude is given indecibels,i.e., a value for the magnitude$|H|$is plotted on the axis at$20\log _{10}|H|$.

TheBode phase plotis the graph of thephase,commonly expressed in degrees, of the transfer function$\arg \left(H(s=j\omega )\right)$as a function of$\omega$.The phase is plotted on the same logarithmic$\omega$-axis as the magnitude plot, but the value for the phase is plotted on a linear vertical axis.

Frequency response

This section illustrates that a Bode plot is a visualization of the frequency response of a system.

Consider alinear, time-invariantsystem with transfer function$H(s)$.Assume that the system is subject to a sinusoidal input with frequency$\omega$,

$u(t)=\sin(\omega t),$

that is applied persistently, i.e. from a time$-\infty$to a time$t$.The response will be of the form

$y(t)=y_{0}\sin(\omega t+\varphi ),$

i.e., also a sinusoidal signal with amplitude$y_{0}$shifted by a phase$\varphi$with respect to the input.

It can be shownthat the magnitude of the response is

$y_{0}=|H(\mathrm {j} \omega )|$(1)

and that the phase shift is

$\varphi =\arg H(\mathrm {j} \omega ).$(2)

In summary, subjected to an input with frequency$\omega$,the system responds at the same frequency with an output that is amplified by a factor$|H(\mathrm {j} \omega )|$and phase-shifted by$\arg H(\mathrm {j} \omega )$.These quantities, thus, characterize the frequency response and are shown in the Bode plot.

Rules for handmade Bode plot

For many practical problems, the detailed Bode plots can be approximated with straight-line segments that areasymptotesof the precise response. The effect of each of the terms of a multiple elementtransfer functioncan be approximated by a set of straight lines on a Bode plot. This allows a graphical solution of the overall frequency response function. Before widespread availability of digital computers, graphical methods were extensively used to reduce the need for tedious calculation; a graphical solution could be used to identify feasible ranges of parameters for a new design.

The premise of a Bode plot is that one can consider the log of a function in the form

$f(x)=A\prod (x-c_{n})^{a_{n}}$

as a sum of the logs of itszeros and poles:

$\log(f(x))=\log(A)+\sum a_{n}\log(x-c_{n}).$

This idea is used explicitly in the method for drawing phase diagrams. The method for drawing amplitude plots implicitly uses this idea, but since the log of the amplitude of each pole or zero always starts at zero and only has one asymptote change (the straight lines), the method can be simplified.

Straight-line amplitude plot

Amplitude decibels is usually done using${\text{dB}}=20\log _{10}(X)$to define decibels. Given a transfer function in the form

$H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}},$

where$x_{n}$and$y_{n}$are constants,$s=\mathrm {j} \omega$,$a_{n},b_{n}>0$,and$H$is the transfer function:

• At every value ofswhere$\omega =x_{n}$(a zero),increasethe slope of the line by$20a_{n}\ {\text{dB}}$perdecade.
• At every value ofswhere$\omega =y_{n}$(a pole),decreasethe slope of the line by$20b_{n}\ {\text{dB}}$per decade.
• The initial value of the graph depends on the boundaries. The initial point is found by putting the initial angular frequency$\omega$into the function and finding$|H(\mathrm {j} \omega )|$.
• The initial slope of the function at the initial value depends on the number and order of zeros and poles that are at values below the initial value, and is found using the first two rules.

To handle irreducible 2nd-order polynomials,$ax^{2}+bx+c$can, in many cases, be approximated as$({\sqrt {a}}x+{\sqrt {c}})^{2}$.

Note that zeros and poles happen when$\omega$isequal toa certain$x_{n}$or$y_{n}$.This is because the function in question is the magnitude of$H(\mathrm {j} \omega )$,and since it is a complex function,$|H(\mathrm {j} \omega )|={\sqrt {H\cdot H^{*}}}$.Thus at any place where there is a zero or pole involving the term$(s+x_{n})$,the magnitude of that term is${\sqrt {(x_{n}+\mathrm {j} \omega )(x_{n}-\mathrm {j} \omega )}}={\sqrt {x_{n}^{2}+\omega ^{2}}}$.

Corrected amplitude plot

To correct a straight-line amplitude plot:

• At every zero, put a point$3a_{n}\ {\text{dB}}$abovethe line.
• At every pole, put a point$3b_{n}\ {\text{dB}}$belowthe line.
• Draw a smooth curve through those points using the straight lines as asymptotes (lines which the curve approaches).

Note that this correction method does not incorporate how to handle complex values of$x_{n}$or$y_{n}$.In the case of an irreducible polynomial, the best way to correct the plot is to actually calculate the magnitude of the transfer function at the pole or zero corresponding to the irreducible polynomial, and put that dot over or under the line at that pole or zero.

Straight-line phase plot

Given a transfer function in the same form as above,

$H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}},$

the idea is to draw separate plots for each pole and zero, then add them up. The actual phase curve is given by

$\varphi (s)=-\arctan {\frac {\operatorname {Im} [H(s)]}{\operatorname {Re} [H(s)]}}.$

To draw the phase plot, foreachpole and zero:

• If$A$is positive, start line (with zero slope) at 0°.
• If$A$is negative, start line (with zero slope) at −180°.
• If the sum of the number of unstable zeros and poles is odd, add 180° to that basis.
• At every$\omega =|x_{n}|$(for stable zeros$-\operatorname {Re} (z)<0$),increasethe slope by$45a_{n}$degrees per decade, beginning one decade before$\omega =|x_{n}|$(e.g.,$|x_{n}|/10$).
• At every$\omega =|y_{n}|$(for stable poles$-\operatorname {Re} (p)<0$),decreasethe slope by$45b_{n}$degrees per decade, beginning one decade before$\omega =|y_{n}|$(e.g.,$|y_{n}|/10$).
• "Unstable" (right half-plane) poles and zeros ($\operatorname {Re} (s)>0$) have opposite behavior.
• Flatten the slope again when the phase has changed by$90a_{n}$degrees (for a zero) or$90b_{n}$degrees (for a pole).
• After plotting one line for each pole or zero, add the lines together to obtain the final phase plot; that is, the final phase plot is the superposition of each earlier phase plot.

Example

To create a straight-line plot for a first-order (one-pole) low-pass filter, one considers the normalized form of the transfer function in terms of the angular frequency:

$H_{\text{lp}}(\mathrm {j} \omega )={\frac {1}{1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}}}.$

The Bode plot is shown in Figure 1(b) above, and construction of the straight-line approximation is discussed next.

Magnitude plot

The magnitude (indecibels) of the transfer function above (normalized and converted to angular-frequency form), given by the decibel gain expression$A_{\text{vdB}}$:

${\begin{aligned}A_{\text{vdB}}&=20\log |H_{\text{lp}}(\mathrm {j} \omega )|\\&=20\log {\frac {1}{\left|1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}\right|}}\\&=-20\log \left|1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}\right|\\&=-10\log \left(1+{\frac {\omega ^{2}}{\omega _{\text{c}}^{2}}}\right).\end{aligned}}$

Then plotted versus input frequency$\omega$on a logarithmic scale, can be approximated bytwo lines,forming the asymptotic (approximate) magnitude Bode plot of the transfer function:

• The first line for angular frequencies below$\omega _{\text{c}}$is a horizontal line at 0 dB, since at low frequencies the$\omega /\omega _{\text{c}}$term is small and can be neglected, making the decibel gain equation above equal to zero.
• The second line for angular frequencies above$\omega _{\text{c}}$is a line with a slope of −20 dB per decade, since at high frequencies the$\omega /\omega _{\text{c}}$term dominates, and the decibel gain expression above simplifies to$-20\log(\omega /\omega _{\text{c}})$,which is a straight line with a slope of −20 dB per decade.

These two lines meet at thecorner frequency$\omega _{\text{c}}$.From the plot, it can be seen that for frequencies well below the corner frequency, the circuit has an attenuation of 0 dB, corresponding to a unity pass-band gain, i.e. the amplitude of the filter output equals the amplitude of the input. Frequencies above the corner frequency are attenuated – the higher the frequency, the higher theattenuation.

Phase plot

The phase Bode plot is obtained by plotting the phase angle of the transfer function given by

$\arg H_{\text{lp}}(\mathrm {j} \omega )=-\tan ^{-1}{\frac {\omega }{\omega _{\text{c}}}}$

versus$\omega$,where$\omega$and$\omega _{\text{c}}$are the input and cutoff angular frequencies respectively. For input frequencies much lower than corner, the ratio$\omega /\omega _{\text{c}}$is small, and therefore the phase angle is close to zero. As the ratio increases, the absolute value of the phase increases and becomes −45° when$\omega =\omega _{\text{c}}$.As the ratio increases for input frequencies much greater than the corner frequency, the phase angle asymptotically approaches −90°. The frequency scale for the phase plot is logarithmic.

Normalized plot

The horizontal frequency axis, in both the magnitude and phase plots, can be replaced by the normalized (nondimensional) frequency ratio$\omega /\omega _{\text{c}}$.In such a case the plot is said to be normalized, and units of the frequencies are no longer used, since all input frequencies are now expressed as multiples of the cutoff frequency$\omega _{\text{c}}$.

An example with zero and pole

Figures 2-5 further illustrate construction of Bode plots. This example with both a pole and a zero shows how to use superposition. To begin, the components are presented separately.

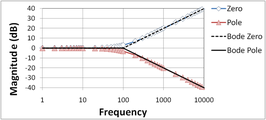
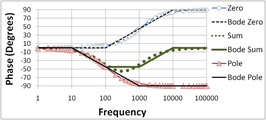
Figure 2 shows the Bode magnitude plot for a zero and a low-pass pole, and compares the two with the Bode straight line plots. The straight-line plots are horizontal up to the pole (zero) location and then drop (rise) at 20 dB/decade. The second Figure 3 does the same for the phase. The phase plots are horizontal up to a frequency factor of ten below the pole (zero) location and then drop (rise) at 45°/decade until the frequency is ten times higher than the pole (zero) location. The plots then are again horizontal at higher frequencies at a final, total phase change of 90°.

Figure 4 and Figure 5 show how superposition (simple addition) of a pole and zero plot is done. The Bode straight line plots again are compared with the exact plots. The zero has been moved to higher frequency than the pole to make a more interesting example. Notice in Figure 4 that the 20 dB/decade drop of the pole is arrested by the 20 dB/decade rise of the zero resulting in a horizontal magnitude plot for frequencies above the zero location. Notice in Figure 5 in the phase plot that the straight-line approximation is pretty approximate in the region where both pole and zero affect the phase. Notice also in Figure 5 that the range of frequencies where the phase changes in the straight line plot is limited to frequencies a factor of ten above and below the pole (zero) location. Where the phase of the pole and the zero both are present, the straight-line phase plot is horizontal because the 45°/decade drop of the pole is arrested by the overlapping 45°/decade rise of the zero in the limited range of frequencies where both are active contributors to the phase.

• Example with pole and zero
• 
  Figure 2: Bode magnitude plot for zero and low-pass pole; curves labeled "Bode" are the straight-line Bode plots
• 
  Figure 3: Bode phase plot for zero and low-pass pole; curves labeled "Bode" are the straight-line Bode plots
• 
  Figure 4: Bode magnitude plot for pole-zero combination; the location of the zero is ten times higher than in Figures 2 and 3; curves labeled "Bode" are the straight-line Bode plots
• 
  Figure 5: Bode phase plot for pole-zero combination; the location of the zero is ten times higher than in Figures 2 and 3; curves labeled "Bode" are the straight-line Bode plots

Gain margin and phase margin

See also:Phase margin

Bode plots are used to assess the stability ofnegative-feedback amplifiersby finding the gain andphase marginsof an amplifier. The notion of gain and phase margin is based upon the gain expression for a negative feedback amplifier given by

$A_{\text{FB}}={\frac {A_{\text{OL}}}{1+\beta A_{\text{OL}}}},$

whereA_FBis the gain of the amplifier with feedback (theclosed-loop gain),βis thefeedback factor,andA_OLis the gain without feedback (theopen-loop gain). The gainA_OLis a complex function of frequency, with both magnitude and phase.Examination of this relation shows the possibility of infinite gain (interpreted as instability) if the product βA_OL= −1 (that is, the magnitude of βA_OLis unity and its phase is −180°, the so-calledBarkhausen stability criterion). Bode plots are used to determine just how close an amplifier comes to satisfying this condition.

Key to this determination are two frequencies. The first, labeled here asf₁₈₀,is the frequency where the open-loop gain flips sign. The second, labeled heref_{0 dB},is the frequency where the magnitude of the product |βA_OL| = 1 = 0 dB. That is, frequencyf₁₈₀is determined by the condition

$\beta A_{\text{OL}}(f_{180})=-|\beta A_{\text{OL}}(f_{180})|=-|\beta A_{\text{OL}}|_{180},$

where vertical bars denote themagnitude of a complex number,and frequencyf_{0 dB}is determined by the condition

$|\beta A_{\text{OL}}(f_{\text{0 dB}})|=1.$

One measure of proximity to instability is thegain margin.The Bode phase plot locates the frequency where the phase of βA_OLreaches −180°, denoted here as frequencyf₁₈₀.Using this frequency, the Bode magnitude plot finds the magnitude of βA_OL.If |βA_OL|₁₈₀≥ 1, the amplifier is unstable, as mentioned. If |βA_OL|₁₈₀< 1, instability does not occur, and the separation in dB of the magnitude of |βA_OL|₁₈₀from |βA_OL| = 1 is called thegain margin.Because a magnitude of 1 is 0 dB, the gain margin is simply one of the equivalent forms:$20\log _{10}|\beta A_{\text{OL}}|_{180}=20\log _{10}|A_{\text{OL}}|-20\log _{10}\beta ^{-1}$.

Another equivalent measure of proximity to instability is thephase margin.The Bode magnitude plot locates the frequency where the magnitude of |βA_OL| reaches unity, denoted here as frequencyf_{0 dB}.Using this frequency, the Bode phase plot finds the phase of βA_OL.If the phase of βA_OL(f_{0 dB}) > −180°, the instability condition cannot be met at any frequency (because its magnitude is going to be < 1 whenf=f₁₈₀), and the distance of the phase atf_{0 dB}in degrees above −180° is called thephase margin.

If a simpleyesornoon the stability issue is all that is needed, the amplifier is stable iff_{0 dB}<f₁₈₀.This criterion is sufficient to predict stability only for amplifiers satisfying some restrictions on their pole and zero positions (minimum phasesystems). Although these restrictions usually are met, if they are not, then another method must be used, such as theNyquist plot. Optimal gain and phase margins may be computed usingNevanlinna–Pick interpolationtheory.

Examples using Bode plots

Figures 6 and 7 illustrate the gain behavior and terminology. For a three-pole amplifier, Figure 6 compares the Bode plot for the gain without feedback (theopen-loopgain)A_OLwith the gain with feedbackA_FB(theclosed-loopgain). Seenegative feedback amplifierfor more detail.

In this example,A_OL= 100 dB at low frequencies, and 1 / β = 58 dB. At low frequencies,A_FB≈ 58 dB as well.

Because the open-loop gainA_OLis plotted and not the product βA_OL,the conditionA_OL= 1 / β decidesf_{0 dB}.The feedback gain at low frequencies and for largeA_OLisA_FB≈ 1 / β (look at the formula for the feedback gain at the beginning of this section for the case of large gainA_OL), so an equivalent way to findf_{0 dB}is to look where the feedback gain intersects the open-loop gain. (Frequencyf_{0 dB}is needed later to find the phase margin.)

Near this crossover of the two gains atf_{0 dB},the Barkhausen criteria are almost satisfied in this example, and the feedback amplifier exhibits a massive peak in gain (it would be infinity if βA_OL= −1). Beyond the unity gain frequencyf_{0 dB},the open-loop gain is sufficiently small thatA_FB≈A_OL(examine the formula at the beginning of this section for the case of smallA_OL).

Figure 7 shows the corresponding phase comparison: the phase of the feedback amplifier is nearly zero out to the frequencyf₁₈₀where the open-loop gain has a phase of −180°. In this vicinity, the phase of the feedback amplifier plunges abruptly downward to become almost the same as the phase of the open-loop amplifier. (Recall,A_FB≈A_OLfor smallA_OL.)

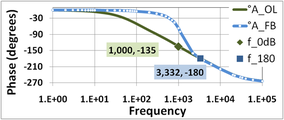
Comparing the labeled points in Figure 6 and Figure 7, it is seen that the unity gain frequencyf_{0 dB}and the phase-flip frequencyf₁₈₀are very nearly equal in this amplifier,f₁₈₀≈f_{0 dB}≈ 3.332 kHz, which means the gain margin and phase margin are nearly zero. The amplifier is borderline stable.

Figures 8 and 9 illustrate the gain margin and phase margin for a different amount of feedback β. The feedback factor is chosen smaller than in Figure 6 or 7, moving the condition | βA_OL| = 1 to lower frequency. In this example, 1 / β = 77 dB, and at low frequenciesA_FB≈ 77 dB as well.

Figure 8 shows the gain plot. From Figure 8, the intersection of 1 / β andA_OLoccurs atf_{0 dB}= 1 kHz. Notice that the peak in the gainA_FBnearf_{0 dB}is almost gone.

Figure 9 is the phase plot. Using the value off_{0 dB}= 1 kHz found above from the magnitude plot of Figure 8, the open-loop phase atf_{0 dB}is −135°, which is a phase margin of 45° above −180°.

Using Figure 9, for a phase of −180° the value off₁₈₀= 3.332 kHz (the same result as found earlier, of course). The open-loop gain from Figure 8 atf₁₈₀is 58 dB, and 1 / β = 77 dB, so the gain margin is 19 dB.

Stability is not the sole criterion for amplifier response, and in many applications a more stringent demand than stability is goodstep response.As arule of thumb,good step response requires a phase margin of at least 45°, and often a margin of over 70° is advocated, particularly where component variation due to manufacturing tolerances is an issue.See also the discussion of phase margin in thestep responsearticle.

• Examples
• 
  Figure 6: Gain of feedback amplifierA_FBin dB and corresponding open-loop amplifierA_OL.Parameter 1/β = 58 dB, and at low frequenciesA_FB≈ 58 dB as well. The gain margin in this amplifier is nearly zero because | βA_OL| = 1 occurs at almostf=f_180°.
• 
  Figure 7: Phase of feedback amplifier°A_FBin degrees and corresponding open-loop amplifier°A_OL.The phase margin in this amplifier is nearly zero because the phase-flip occurs at almost the unity gain frequencyf=f_{0 dB}where | βA_OL| = 1.
• 
  Figure 8: Gain of feedback amplifierA_FBin dB and corresponding open-loop amplifierA_OL.In this example, 1 / β = 77 dB. The gain margin in this amplifier is 19 dB.
• 
  Figure 9: Phase of feedback amplifierA_FBin degrees and corresponding open-loop amplifierA_OL.The phase margin in this amplifier is 45°.

Bode plotter

Figure 10: Amplitude diagram of a 10th-orderelectronic filterplotted using a Bode plotter

The Bode plotter is an electronic instrument resembling anoscilloscope,which produces a Bode diagram, or a graph, of a circuit's voltage gain or phase shift plotted againstfrequencyin a feedback control system or a filter. An example of this is shown in Figure 10. It is extremely useful for analyzing and testing filters and the stability offeedbackcontrol systems, through the measurement of corner (cutoff) frequencies and gain and phase margins.

This is identical to the function performed by avector network analyzer,but the network analyzer is typically used at much higher frequencies.

For education and research purposes, plotting Bode diagrams for given transfer functions facilitates better understanding and getting faster results (see external links).

Related plots

Main articles:Nyquist plotandNichols plot

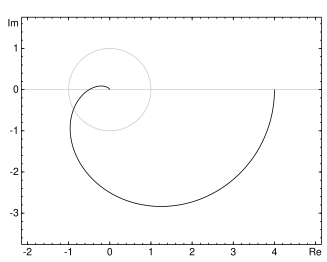
Two related plots that display the same data in differentcoordinate systemsare theNyquist plotand theNichols plot.These areparametric plots,with frequency as the input and magnitude and phase of the frequency response as the output. The Nyquist plot displays these inpolar coordinates,with magnitude mapping to radius and phase to argument (angle). The Nichols plot displays these in rectangular coordinates, on thelog scale.

• 
  Figure 11: ANyquist plot.
• 
  Figure 12: ANichols plotof the same response from Figure 11.

See also

• Analog signal processing
• Phase margin
• Bode's sensitivity integral
• Bode's magnitude (gain)–phase relation
• Electrochemical impedance spectroscopy

External links

• How to draw piecewise asymptotic Bode plots
• Gnuplot code for generating Bode plot:DIN-A4 printing template (pdf)