Lattice (order)
This article includes a list of generalreferences,butit lacks sufficient correspondinginline citations.(May 2009) |
| Transitivebinary relations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All definitions tacitly require thehomogeneous relationbetransitive:for allifandthen |
| Algebraic structures |
|---|
Alatticeis an abstract structure studied in themathematicalsubdisciplines oforder theoryandabstract algebra.It consists of apartially ordered setin which every pair of elements has a uniquesupremum(also called a least upper bound orjoin) and a uniqueinfimum(also called a greatest lower bound ormeet). An example is given by thepower setof a set, partially ordered byinclusion,for which the supremum is theunionand the infimum is theintersection.Another example is given by thenatural numbers,partially ordered bydivisibility,for which the supremum is theleast common multipleand the infimum is thegreatest common divisor.
Lattices can also be characterized asalgebraic structuressatisfying certainaxiomaticidentities.Since the two definitions are equivalent, lattice theory draws on bothorder theoryanduniversal algebra.Semilatticesinclude lattices, which in turn includeHeytingandBoolean algebras.Theselattice-likestructures all admitorder-theoreticas well as algebraic descriptions.
The sub-field ofabstract algebrathat studies lattices is calledlattice theory.
Definition
[edit]A lattice can be defined either order-theoretically as a partially ordered set, or as an algebraic structure.
As partially ordered set
[edit]Apartially ordered set(poset)is called alatticeif it is both a join- and a meet-semilattice,i.e. each two-element subsethas ajoin(i.e. least upper bound, denoted by) andduallyameet(i.e. greatest lower bound, denoted by). This definition makesandbinary operations.Both operations are monotone with respect to the given order:andimplies thatand
It follows by aninductionargument that every non-empty finite subset of a lattice has a least upper bound and a greatest lower bound. With additional assumptions, further conclusions may be possible; seeCompleteness (order theory)for more discussion of this subject. That article also discusses how one may rephrase the above definition in terms of the existence of suitableGalois connectionsbetween related partially ordered sets—an approach of special interest for thecategory theoreticapproach to lattices, and forformal concept analysis.
Given a subset of a lattice,meet and join restrict topartial functions– they are undefined if their value is not in the subsetThe resulting structure onis called apartial lattice.In addition to this extrinsic definition as a subset of some other algebraic structure (a lattice), a partial lattice can also be intrinsically defined as a set with two partial binary operations satisfying certain axioms.[1]
As algebraic structure
[edit]Alatticeis analgebraic structure,consisting of a setand two binary, commutative and associativeoperationsandonsatisfying the following axiomatic identities for all elements(sometimes calledabsorption laws):
The following two identities are also usually regarded as axioms, even though they follow from the two absorption laws taken together.[2]These are calledidempotent laws.
These axioms assert that bothandaresemilattices.The absorption laws, the only axioms above in which both meet and join appear, distinguish a lattice from an arbitrary pair of semilattice structures and assure that the two semilattices interact appropriately. In particular, each semilattice is thedualof the other. The absorption laws can be viewed as a requirement that the meet and join semilattices define the samepartial order.
Connection between the two definitions
[edit]An order-theoretic lattice gives rise to the two binary operationsandSince the commutative, associative and absorption laws can easily be verified for these operations, they makeinto a lattice in the algebraic sense.
The converse is also true. Given an algebraically defined latticeone can define a partial orderonby setting for all elementsThe laws of absorption ensure that both definitions are equivalent: and dually for the other direction.
One can now check that the relation ≤ introduced in this way defines a partial ordering within which binary meets and joins are given through the original operationsand
Since the two definitions of a lattice are equivalent, one may freely invoke aspects of either definition in any way that suits the purpose at hand.
Bounded lattice
[edit]Abounded latticeis a lattice that additionally has agreatest element(also calledmaximum,ortopelement, and denoted byorby)and aleast element(also calledminimum,orbottom,denoted byor by),which satisfy
A bounded lattice may also be defined as an algebraic structure of the formsuch thatis a lattice,(the lattice's bottom) is theidentity elementfor the join operationand(the lattice's top) is the identity element for the meet operation
A partially ordered set is a bounded lattice if and only if every finite set of elements (including the empty set) has a join and a meet. For every elementof a poset it isvacuously truethat and and therefore every element of a poset is both an upper bound and a lower bound of the empty set. This implies that the join of an empty set is the least elementand the meet of the empty set is the greatest elementThis is consistent with the associativity and commutativity of meet and join: the join of a union of finite sets is equal to the join of the joins of the sets, and dually, the meet of a union of finite sets is equal to the meet of the meets of the sets, that is, for finite subsetsandof a poset and hold. Takingto be the empty set, and which is consistent with the fact that
Every lattice can be embedded into a bounded lattice by adding a greatest and a least element. Furthermore, every non-empty finite lattice is bounded, by taking the join (respectively, meet) of all elements, denoted by(respectively) whereis the set of all elements.
Connection to other algebraic structures
[edit]Lattices have some connections to the family ofgroup-like algebraic structures.Because meet and join both commute and associate, a lattice can be viewed as consisting of two commutativesemigroupshaving the same domain. For a bounded lattice, these semigroups are in fact commutativemonoids.Theabsorption lawis the only defining identity that is peculiar to lattice theory. A bounded lattice can also be thought of as acommutative rigwithout the distributive axiom.
By commutativity, associativity and idempotence one can think of join and meet as operations on non-empty finite sets, rather than on pairs of elements. In a bounded lattice the join and meet of the empty set can also be defined (asandrespectively). This makes bounded lattices somewhat more natural than general lattices, and many authors require all lattices to be bounded.
The algebraic interpretation of lattices plays an essential role inuniversal algebra.[citation needed]
Examples
[edit]-
Pic. 1:Subsets ofunderset inclusion.The name "lattice" is suggested by the form of theHasse diagramdepicting it.
-
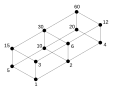
Pic. 2:Lattice of integer divisors of 60, ordered by "divides".
-
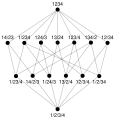
Pic. 3:Lattice ofpartitionsofordered by "refines".
-
Pic. 4:Lattice of positive integers, ordered by
-
Pic. 5:Lattice of nonnegative integer pairs, ordered componentwise.
- For any setthe collection of all subsets of(called thepower setof) can be ordered viasubset inclusionto obtain a lattice bounded byitself and the empty set. In this lattice, the supremum is provided byset unionand the infimum is provided byset intersection(see Pic. 1).
- For any setthe collection of all finite subsets ofordered by inclusion, is also a lattice, and will be bounded if and only ifis finite.
- For any setthe collection of allpartitionsofordered byrefinement,is a lattice (see Pic. 3).
- Thepositive integersin their usual order form an unbounded lattice, under the operations of "min" and "max". 1 is bottom; there is no top (see Pic. 4).
- TheCartesian squareof the natural numbers, ordered so thatifThe pairis the bottom element; there is no top (see Pic. 5).
- The natural numbers also form a lattice under the operations of taking thegreatest common divisorandleast common multiple,withdivisibilityas the order relation:ifdividesis bottom;is top. Pic. 2 shows a finite sublattice.
- Everycomplete lattice(also seebelow) is a (rather specific) bounded lattice. This class gives rise to a broad range of practicalexamples.
- The set ofcompact elementsof anarithmeticcomplete lattice is a lattice with a least element, where the lattice operations are given by restricting the respective operations of the arithmetic lattice. This is the specific property that distinguishes arithmetic lattices fromalgebraic lattices,for which the compacts only form ajoin-semilattice.Both of these classes of complete lattices are studied indomain theory.
Further examples of lattices are given for each of the additional properties discussed below.
Examples of non-lattices
[edit] |
 |
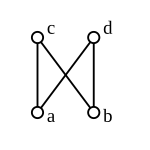 |
Most partially ordered sets are not lattices, including the following.
- A discrete poset, meaning a poset such thatimpliesis a lattice if and only if it has at most one element. In particular the two-element discrete poset is not a lattice.
- Although the setpartially ordered by divisibility is a lattice, the setso ordered is not a lattice because the pair 2, 3 lacks a join; similarly, 2, 3 lacks a meet in
- The setpartially ordered by divisibility is not a lattice. Every pair of elements has an upper bound and a lower bound, but the pair 2, 3 has three upper bounds, namely 12, 18, and 36, none of which is the least of those three under divisibility (12 and 18 do not divide each other). Likewise the pair 12, 18 has three lower bounds, namely 1, 2, and 3, none of which is the greatest of those three under divisibility (2 and 3 do not divide each other).
Morphisms of lattices
[edit]
The appropriate notion of amorphismbetween two lattices flows easily from theabovealgebraic definition. Given two latticesandalattice homomorphismfromLtoMis a functionsuch that for all
Thusis ahomomorphismof the two underlyingsemilattices.When lattices with more structure are considered, the morphisms should "respect" the extra structure, too. In particular, abounded-lattice homomorphism(usually called just "lattice homomorphism" )between two bounded latticesandshould also have the following property:
In the order-theoretic formulation, these conditions just state that a homomorphism of lattices is a functionpreservingbinary meets and joins. For bounded lattices, preservation of least and greatest elements is just preservation of join and meet of the empty set.
Any homomorphism of lattices is necessarilymonotonewith respect to the associated ordering relation; seeLimit preserving function.The converse is not true: monotonicity by no means implies the required preservation of meets and joins (see Pic. 9), although anorder-preservingbijectionis a homomorphism if itsinverseis also order-preserving.
Given the standard definition ofisomorphismsas invertible morphisms, alattice isomorphismis just abijectivelattice homomorphism. Similarly, alattice endomorphismis a lattice homomorphism from a lattice to itself, and alattice automorphismis a bijective lattice endomorphism. Lattices and their homomorphisms form acategory.
Letandbe two lattices with0and1.A homomorphism fromtois called0,1-separatingif and only if(separates0) and(separates 1).
Sublattices
[edit]Asublatticeof a latticeis a subset ofthat is a lattice with the same meet and join operations asThat is, ifis a lattice andis a subset ofsuch that for every pair of elementsbothandare inthenis a sublattice of[3]
A sublatticeof a latticeis aconvex sublatticeofifandimplies thatbelongs tofor all elements
Properties of lattices
[edit]We now introduce a number of important properties that lead to interesting special classes of lattices. One, boundedness, has already been discussed.
Completeness
[edit]A poset is called acomplete latticeifallits subsets have both a join and a meet. In particular, every complete lattice is a bounded lattice. While bounded lattice homomorphisms in general preserve only finite joins and meets, complete lattice homomorphisms are required to preserve arbitrary joins and meets.
Every poset that is a complete semilattice is also a complete lattice. Related to this result is the interesting phenomenon that there are various competing notions of homomorphism for this class of posets, depending on whether they are seen as complete lattices, complete join-semilattices, complete meet-semilattices, or as join-complete or meet-complete lattices.
"Partial lattice" is not the opposite of "complete lattice" – rather, "partial lattice", "lattice", and "complete lattice" are increasingly restrictive definitions.
Conditional completeness
[edit]Aconditionally complete latticeis a lattice in which everynonemptysubsetthat has an upper boundhas a join (that is, a least upper bound). Such lattices provide the most direct generalization of thecompleteness axiomof thereal numbers.A conditionally complete lattice is either a complete lattice, or a complete lattice without its maximum elementits minimum elementor both.[4][5]
Distributivity
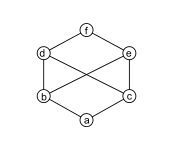
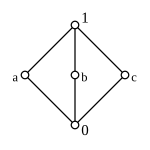
[edit]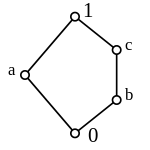 The labelled elements also violate the distributivity equationbut satisfy its dual |
 |
Since lattices come with two binary operations, it is natural to ask whether one of themdistributesover the other, that is, whether one or the other of the followingduallaws holds for every three elements:
- Distributivity ofover
- Distributivity ofover
A lattice that satisfies the first or, equivalently (as it turns out), the second axiom, is called adistributive lattice. The only non-distributive lattices with fewer than 6 elements are called M3and N5;[6]they are shown in Pictures 10 and 11, respectively. A lattice is distributive if and only if it does not have asublatticeisomorphic to M3or N5.[7]Each distributive lattice is isomorphic to a lattice of sets (with union and intersection as join and meet, respectively).[8]
For an overview of stronger notions of distributivity that are appropriate for complete lattices and that are used to define more special classes of lattices such asframesandcompletely distributive lattices,seedistributivity in order theory.
Modularity
[edit]For some applications the distributivity condition is too strong, and the following weaker property is often useful. A latticeismodularif, for all elementsthe following identity holds:
(Modular identity)
This condition is equivalent to the following axiom:
implies(Modular law)
A lattice is modular if and only if it does not have asublatticeisomorphic to N5(shown in Pic. 11).[7]
Besides distributive lattices, examples of modular lattices are the lattice of submodules of amodule(hencemodular), the lattice oftwo-sided idealsof aring,and the lattice ofnormal subgroupsof agroup.Theset of first-order termswith the ordering "is more specific than" is a non-modular lattice used inautomated reasoning.
Semimodularity
[edit]A finite lattice is modular if and only if it is both upper and lowersemimodular.For a graded lattice, (upper) semimodularity is equivalent to the following condition on the rank function
Another equivalent (for graded lattices) condition isBirkhoff's condition:
- for eachandinifandboth coverthencovers bothand
A lattice is called lower semimodular if its dual is semimodular. For finite lattices this means that the previous conditions hold withandexchanged, "covers" exchanged with "is covered by", and inequalities reversed.[9]
Continuity and algebraicity
[edit]Indomain theory,it is natural to seek to approximate the elements in a partial order by "much simpler" elements. This leads to the class ofcontinuous posets,consisting of posets where every element can be obtained as the supremum of adirected setof elements that areway-belowthe element. If one can additionally restrict these to thecompact elementsof a poset for obtaining these directed sets, then the poset is evenalgebraic.Both concepts can be applied to lattices as follows:
- Acontinuous latticeis a complete lattice that is continuous as a poset.
- Analgebraic latticeis a complete lattice that is algebraic as a poset.
Both of these classes have interesting properties. For example, continuous lattices can be characterized as algebraic structures (with infinitary operations) satisfying certain identities. While such a characterization is not known for algebraic lattices, they can be described "syntactically" viaScott information systems.
Complements and pseudo-complements
[edit]Letbe a bounded lattice with greatest element 1 and least element 0. Two elementsandofarecomplementsof each other if and only if:
In general, some elements of a bounded lattice might not have a complement, and others might have more than one complement. For example, the setwith its usual ordering is a bounded lattice, anddoes not have a complement. In the bounded lattice N5,the elementhas two complements, viz.and(see Pic. 11). A bounded lattice for which every element has a complement is called acomplemented lattice.
A complemented lattice that is also distributive is aBoolean algebra.For a distributive lattice, the complement ofwhen it exists, is unique.
In the case that the complement is unique, we writeand equivalently,The corresponding unaryoperationovercalled complementation, introduces an analogue of logicalnegationinto lattice theory.
Heyting algebrasare an example of distributive lattices where some members might be lacking complements. Every elementof a Heyting algebra has, on the other hand, apseudo-complement,also denotedThe pseudo-complement is the greatest elementsuch thatIf the pseudo-complement of every element of a Heyting algebra is in fact a complement, then the Heyting algebra is in fact a Boolean algebra.
Jordan–Dedekind chain condition
[edit]Achainfromtois a setwhere Thelengthof this chain isn,or one less than its number of elements. A chain ismaximalifcoversfor all
If for any pair,andwhereall maximal chains fromtohave the same length, then the lattice is said to satisfy theJordan–Dedekind chain condition.
Graded/ranked
[edit]A latticeis calledgraded,sometimesranked(but seeRanked posetfor an alternative meaning), if it can be equipped with arank functionsometimes to,compatible with the ordering (sowhenever) such that whenevercoversthenThe value of the rank function for a lattice element is called itsrank.
A lattice elementis said tocoveranother elementifbut there does not exist asuch that Here,meansand
Free lattices
[edit]Any setmay be used to generate thefree semilatticeThe free semilattice is defined to consist of all of the finite subsets ofwith the semilattice operation given by ordinaryset union.The free semilattice has theuniversal property.For thefree latticeover a setWhitmangave a construction based on polynomials over's members.[10][11]
Important lattice-theoretic notions
[edit]We now define some order-theoretic notions of importance to lattice theory. In the following, letbe an element of some latticeis called:
- Join irreducibleifimpliesfor allIfhas a bottom elementsome authors require.[12]When the first condition is generalized to arbitrary joinsis calledcompletely join irreducible(or-irreducible). The dual notion ismeet irreducibility(-irreducible). For example, in Pic. 2, the elements 2, 3, 4, and 5 are join irreducible, while 12, 15, 20, and 30 are meet irreducible. Depending on definition, the bottom element 1 and top element 60 may or may not be considered join irreducible and meet irreducible, respectively. In the lattice ofreal numberswith the usual order, each element is join irreducible, but none is completely join irreducible.
- Join primeifimpliesAgain some authors require,although this is unusual.[13]This too can be generalized to obtain the notioncompletely join prime.The dual notion ismeet prime.Every join-prime element is also join irreducible, and every meet-prime element is also meet irreducible. The converse holds ifis distributive.
Lethave a bottom element 0. An elementofis anatomifand there exists no elementsuch thatThenis called:
- Atomicif for every nonzero elementofthere exists an atomofsuch that[14]
- Atomisticif every element ofis asupremumof atoms.[15]
However, many sources and mathematical communities use the term "atomic" to mean "atomistic" as defined above.[citation needed]
The notions ofidealsand the dual notion offiltersrefer to particular kinds ofsubsetsof a partially ordered set, and are therefore important for lattice theory. Details can be found in the respective entries.
See also
[edit]- Join and meet– Concept in order theory
- Map of lattices– Concept in mathematics
- Orthocomplemented lattice
- Total order– Order whose elements are all comparable
- Ideal– Nonempty, upper-bounded, downward-closed subset andfilter(dual notions)
- Skew lattice– Algebraic Structure(generalization to non-commutative join and meet)
- Eulerian lattice
- Post's lattice– lattice of all clones (sets of logical connectives closed under composition and containing all projections) on a two-element set {0, 1}, ordered by inclusion
- Tamari lattice– mathematical object formed by an order on the way of parenthesing an expression
- Young–Fibonacci lattice
- 0,1-simple lattice
Applications that use lattice theory
[edit]Note that in many applications the sets are only partial lattices: not every pair of elements has a meet or join.
- Pointless topology
- Lattice of subgroups
- Spectral space
- Invariant subspace
- Closure operator
- Abstract interpretation
- Subsumption lattice
- Fuzzy settheory
- Algebraizations of first-order logic
- Semantics of programming languages
- Domain theory
- Ontology (computer science)
- Multiple inheritance
- Formal concept analysisandLattice Miner(theory and tool)
- Bloom filter
- Information flow
- Ordinal optimization
- Quantum logic
- Median graph
- Knowledge space
- Regular language learning
- Analogical modeling
Notes
[edit]- ^Grätzer 2003,p.52.
- ^Birkhoff 1948,p.18."sinceand dually ". Birkhoff attributes this toDedekind 1897,p.8
- ^Burris, Stanley N., and Sankappanavar, H. P., 1981.A Course in Universal Algebra.Springer-Verlag.ISBN3-540-90578-2.
- ^Baker, Kirby (2010)."Complete Lattices"(PDF).UCLA Department of Mathematics.Retrieved8 June2022.
- ^Kaplansky, Irving (1972).Set Theory and Metric Spaces(2nd ed.). New York City:AMS Chelsea Publishing.p. 14.ISBN9780821826942.
- ^Davey & Priestley (2002),Exercise 4.1,p. 104.
- ^abDavey & Priestley (2002),Theorem 4.10,p. 89.
- ^Davey & Priestley (2002),Theorem 10.21,pp. 238–239.
- ^Stanley, Richard P(1997),Enumerative Combinatorics (vol. 1),Cambridge University Press, pp. 103–104,ISBN0-521-66351-2
- ^Philip Whitman (1941). "Free Lattices I".Annals of Mathematics.42(1): 325–329.doi:10.2307/1969001.JSTOR1969001.
- ^Philip Whitman (1942). "Free Lattices II".Annals of Mathematics.43(1): 104–115.doi:10.2307/1968883.JSTOR1968883.
- ^Davey & Priestley 2002,p. 53.
- ^Hoffmann, Rudolf-E. (1981).Continuous posets, prime spectra of completely distributive complete lattices, and Hausdorff compactifications.Continuous Lattices. Vol. 871. pp. 159–208.doi:10.1007/BFb0089907.
- ^Grätzer 2003,p. 246, Exercise 3.
- ^Grätzer 2003,p. 234, after Def.1.
References
[edit]Monographs available free online:
- Burris, Stanley N., and Sankappanavar, H. P., 1981.A Course in Universal Algebra.Springer-Verlag.ISBN3-540-90578-2.
- Jipsen, Peter, and Henry Rose,Varieties of Lattices,Lecture Notes in Mathematics 1533, Springer Verlag, 1992.ISBN0-387-56314-8.
Elementary texts recommended for those with limitedmathematical maturity:
- Donnellan, Thomas, 1968.Lattice Theory.Pergamon.
- Grätzer, George,1971.Lattice Theory: First concepts and distributive lattices.W. H. Freeman.
The standard contemporary introductory text, somewhat harder than the above:
- Davey, B. A.;Priestley, H. A.(2002),Introduction to Lattices and Order,Cambridge University Press,ISBN978-0-521-78451-1
Advanced monographs:
- Garrett Birkhoff,1967.Lattice Theory,3rd ed. Vol. 25 of AMS Colloquium Publications.American Mathematical Society.
- Robert P. Dilworthand Crawley, Peter, 1973.Algebraic Theory of Lattices.Prentice-Hall.ISBN978-0-13-022269-5.
- Grätzer, George (2003).General Lattice Theory(Second ed.). Basel: Birkhäuser.ISBN978-3-7643-6996-5.
On free lattices:
- R. Freese, J. Jezek, and J. B. Nation, 1985. "Free Lattices". Mathematical Surveys and Monographs Vol. 42.Mathematical Association of America.
- Johnstone, P. T.,1982.Stone spaces.Cambridge Studies in Advanced Mathematics 3. Cambridge University Press.
On the history of lattice theory:
- Štĕpánka Bilová (2001). Eduard Fuchs (ed.).Lattice theory — its birth and life(PDF).Prometheus. pp. 250–257.
- Birkhoff, Garrett (1948).Lattice Theory(2nd ed.).Textbook with numerous attributions in the footnotes.
- Schlimm, Dirk (November 2011). "On the creative role of axiomatics. The discovery of lattices by Schröder, Dedekind, Birkhoff, and others".Synthese.183(1): 47–68.CiteSeerX10.1.1.594.8898.doi:10.1007/s11229-009-9667-9.S2CID11012081.Summary of the history of lattices.
- Dedekind, Richard(1897),"Über Zerlegungen von Zahlen durch ihre grössten gemeinsamen Teiler"(PDF),Braunschweiger Festschrift,doi:10.24355/dbbs.084-200908140200-2
On applications of lattice theory:
- Garrett Birkhoff (1967). James C. Abbot (ed.).What can Lattices do for you?.Van Nostrand.Table of contents
External links
[edit]- "Lattice-ordered group",Encyclopedia of Mathematics,EMS Press,2001 [1994]
- Weisstein, Eric W."Lattice".MathWorld.
- J.B. Nation,Notes on Lattice Theory,course notes, revised 2017.
- Ralph Freese,"Lattice Theory Homepage".
- OEISsequence A006966 (Number of unlabeled lattices withnelements)