Cantor set

Not to be confused withCantor space.

Inmathematics,theCantor setis asetof points lying on a singleline segmentthat has a number of unintuitive properties. It was discovered in 1874 byHenry John Stephen Smithand mentioned by German mathematicianGeorg Cantorin 1883.

Through consideration of this set, Cantor and others helped lay the foundations of modernpoint-set topology.The most common construction is theCantor ternary set,built by removing the middle third of a line segment and then repeating the process with the remaining shorter segments. Cantor mentioned this ternary construction only in passing, as an example of aperfect setthat isnowhere dense(,Anmerkungen zu §10, /p. 590).

More generally, in topology,aCantor spaceis a topological space homeomorphic to the Cantor ternary set (equipped with its subspace topology). By a theorem ofL. E. J. Brouwer,this is equivalent to being perfect, nonempty, compact, metrizable and zero dimensional.

Expansion of a Cantor set. Each point in the set is represented here by a vertical line.

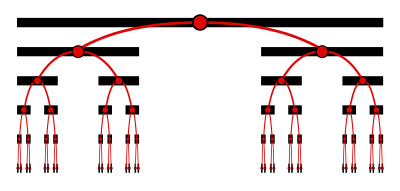
Construction and formula of the ternary set

The Cantor ternary set${\mathcal {C}}$is created by iteratively deleting theopenmiddle third from a set of line segments. One starts by deleting the open middle third${\textstyle \left({\frac {1}{3}},{\frac {2}{3}}\right)}$from theinterval$\textstyle \left[0,1\right]$,leaving two line segments:${\textstyle \left[0,{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},1\right]}$.Next, the open middle third of each of these remaining segments is deleted, leaving four line segments:${\textstyle \left[0,{\frac {1}{9}}\right]\cup \left[{\frac {2}{9}},{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},{\frac {7}{9}}\right]\cup \left[{\frac {8}{9}},1\right]}$. The Cantor ternary set contains all points in the interval$[0,1]$that are not deleted at any step in thisinfinite process.The same facts can be described recursively by setting

$C_{0}:=[0,1]$

and

$C_{n}:={\frac {C_{n-1}}{3}}\cup \left({\frac {2}{3}}+{\frac {C_{n-1}}{3}}\right)={\frac {1}{3}}{\bigl (}C_{n-1}\cup \left(2+C_{n-1}\right){\bigr )}$

for$n\geq 1$,so that

${\mathcal {C}}:=$${\color {Blue}\lim _{n\to \infty }C_{n}}$$=\bigcap _{n=0}^{\infty }C_{n}=\bigcap _{n=m}^{\infty }C_{n}$  for any  $m\geq 0$.

The first six steps of this process are illustrated below.

Using the idea of self-similar transformations,$T_{L}(x)=x/3,$$T_{R}(x)=(2+x)/3$and$C_{n}=T_{L}(C_{n-1})\cup T_{R}(C_{n-1}),$the explicit closed formulas for the Cantor set are

${\mathcal {C}}=[0,1]\,\setminus \,\bigcup _{n=0}^{\infty }\bigcup _{k=0}^{3^{n}-1}\left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)\!,$

where every middle third is removed as the open interval${\textstyle \left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)}$from theclosed interval${\textstyle \left[{\frac {3k+0}{3^{n+1}}},{\frac {3k+3}{3^{n+1}}}\right]=\left[{\frac {k+0}{3^{n}}},{\frac {k+1}{3^{n}}}\right]}$surrounding it, or

${\mathcal {C}}=\bigcap _{n=1}^{\infty }\bigcup _{k=0}^{3^{n-1}-1}\left(\left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]\right)\!,$

where the middle third${\textstyle \left({\frac {3k+1}{3^{n}}},{\frac {3k+2}{3^{n}}}\right)}$of the foregoing closed interval${\textstyle \left[{\frac {k+0}{3^{n-1}}},{\frac {k+1}{3^{n-1}}}\right]=\left[{\frac {3k+0}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]}$is removed by intersecting with${\textstyle \left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]\!.}$

This process of removing middle thirds is a simple example of afinite subdivision rule.The complement of the Cantor ternary set is an example of afractal string.

In arithmetical terms, the Cantor set consists of allreal numbersof theunit interval$[0,1]$that do not require the digit 1 in order to be expressed as aternary(base 3) fraction. As the above diagram illustrates, each point in the Cantor set is uniquely located by a path through an infinitely deepbinary tree,where the path turns left or right at each level according to which side of a deleted segment the point lies on. Representing each left turn with 0 and each right turn with 2 yields the ternary fraction for a point.

Mandelbrot's construction by "curdling"

InThe Fractal Geometry of Nature,mathematicianBenoit Mandelbrotprovides a whimsical thought experiment to assist non-mathematical readers in imagining the construction of${\mathcal {C}}$.His narrative begins with imagining a bar, perhaps of lightweight metal, in which the bar's matter "curdles" by iteratively shifting towards its extremities. As the bar's segments become smaller, they become thin, dense slugs that eventually grow too small and faint to see.

CURDLING: The construction of the Cantor bar results from the process I call curdling. It begins with a round bar. It is best to think of it as having a very low density. Then matter "curdles" out of this bar's middle third into the end thirds, so that the positions of the latter remain unchanged. Next matter curdles out of the middle third of each end third into its end thirds, and so on ad infinitum until one is left with an infinitely large number of infinitely thin slugs of infinitely high density. These slugs are spaced along the line in the very specific fashion induced by the generating process. In this illustration, curdling (which eventually requires hammering!) stops when both the printer's press and our eye cease to follow; the last line is indistinguishable from the last but one: each of its ultimate parts is seen as a gray slug rather than two parallel black slugs.

Composition

Since the Cantor set is defined as the set of points not excluded, the proportion (i.e.,measure) of the unit interval remaining can be found by total length removed. This total is thegeometric progression

$\sum _{n=0}^{\infty }{\frac {2^{n}}{3^{n+1}}}={\frac {1}{3}}+{\frac {2}{9}}+{\frac {4}{27}}+{\frac {8}{81}}+\cdots ={\frac {1}{3}}\left({\frac {1}{1-{\frac {2}{3}}}}\right)=1.$

So that the proportion left is 1 − 1 = 0.

This calculation suggests that the Cantor set cannot contain any interval of non-zero length. It may seem surprising that there should be anything left—after all, the sum of the lengths of the removed intervals is equal to the length of the original interval. However, a closer look at the process reveals that there must be something left, since removing the "middle third" of each interval involved removingopen sets(sets that do not include their endpoints). So removing the line segment (1/3,2/3) from the original interval [0, 1] leaves behind the points1/3and2/3.Subsequent steps do not remove these (or other) endpoints, since the intervals removed are always internal to the intervals remaining. So the Cantor set is notempty,and in fact contains anuncountably infinitenumber of points (as follows from the above description in terms of paths in an infinite binary tree).

It may appear thatonlythe endpoints of the construction segments are left, but that is not the case either. The number1/4,for example, has the unique ternary form 0.020202... = 0.02.It is in the bottom third, and the top third of that third, and the bottom third of that top third, and so on. Since it is never in one of the middle segments, it is never removed. Yet it is also not an endpoint of any middle segment, because it is not a multiple of any power of 1/3. All endpoints of segments areterminatingternary fractions and are contained in the set

$\left\{x\in [0,1]\mid \exists i\in \mathbb {N} _{0}:x\,3^{i}\in \mathbb {Z} \right\}\qquad {\Bigl (}\subset \mathbb {N} _{0}\,3^{-\mathbb {N} _{0}}{\Bigr )}$

which is acountably infiniteset. As tocardinality,almost allelements of the Cantor set are not endpoints of intervals, norrationalpoints like 1/4. The whole Cantor set is in fact not countable.

Properties

Cardinality

It can be shown that there are as many points left behind in this process as there were to begin with, and that therefore, the Cantor set isuncountable.To see this, we show that there is afunctionffrom the Cantor set${\mathcal {C}}$to the closed interval [0,1] that issurjective(i.e.fmaps from${\mathcal {C}}$onto [0,1]) so that the cardinality of${\mathcal {C}}$is no less than that of [0,1]. Since${\mathcal {C}}$is asubsetof [0,1], its cardinality is also no greater, so the two cardinalities must in fact be equal, by theCantor–Bernstein–Schröder theorem.

To construct this function, consider the points in the [0, 1] interval in terms of base 3 (orternary) notation. Recall that the proper ternary fractions, more precisely: the elements of${\bigl (}\mathbb {Z} \setminus \{0\}{\bigr )}\cdot 3^{-\mathbb {N} _{0}}$,admit more than one representation in this notation, as for example1/3,that can be written as 0.1₃= 0.10₃,but also as 0.0222...₃= 0.02₃,and2/3,that can be written as 0.2₃= 0.20₃but also as 0.1222...₃= 0.12₃. When we remove the middle third, this contains the numbers with ternary numerals of the form 0.1xxxxx...₃where xxxxx...₃is strictly between 00000...₃and 22222...₃.So the numbers remaining after the first step consist of

• Numbers of the form 0.0xxxxx...₃(including 0.022222...₃= 1/3)
• Numbers of the form 0.2xxxxx...₃(including 0.222222...₃= 1)

This can be summarized by saying that those numbers with a ternary representation such that the first digit after theradix pointis not 1 are the ones remaining after the first step.

The second step removes numbers of the form 0.01xxxx...₃and 0.21xxxx...₃,and (with appropriate care for the endpoints) it can be concluded that the remaining numbers are those with a ternary numeral where neither of the firsttwodigits is 1.

Continuing in this way, for a number not to be excluded at stepn,it must have a ternary representation whosenth digit is not 1. For a number to be in the Cantor set, it must not be excluded at any step, it must admit a numeral representation consisting entirely of 0s and 2s.

It is worth emphasizing that numbers like 1,1/3= 0.1₃and7/9= 0.21₃are in the Cantor set, as they have ternary numerals consisting entirely of 0s and 2s: 1 = 0.222...₃= 0.2₃,1/3= 0.0222...₃= 0.02₃and7/9= 0.20222...₃= 0.202₃. All the latter numbers are "endpoints", and these examples are rightlimit pointsof${\mathcal {C}}$.The same is true for the left limit points of${\mathcal {C}}$,e.g.2/3= 0.1222...₃= 0.12₃= 0.20₃and8/9= 0.21222...₃= 0.212₃= 0.220₃.All these endpoints areproper ternaryfractions (elements of$\mathbb {Z} \cdot 3^{-\mathbb {N} _{0}}$) of the formp/q,where denominatorqis apower of 3when the fraction is in itsirreducibleform.The ternary representation of these fractions terminates (i.e., is finite) or — recall from above that proper ternary fractions each have 2 representations — is infinite and "ends" in either infinitely many recurring 0s or infinitely many recurring 2s. Such a fraction is a leftlimit pointof${\mathcal {C}}$if its ternary representation contains no 1's and "ends" in infinitely many recurring 0s. Similarly, a proper ternary fraction is a right limit point of${\mathcal {C}}$if it again its ternary expansion contains no 1's and "ends" in infinitely many recurring 2s.

This set of endpoints isdensein${\mathcal {C}}$(but not dense in [0, 1]) and makes up acountably infiniteset. The numbers in${\mathcal {C}}$which arenotendpoints also have only 0s and 2s in their ternary representation, but they cannot end in an infinite repetition of the digit 0, nor of the digit 2, because then it would be an endpoint.

The function from${\mathcal {C}}$to [0,1] is defined by taking the ternary numerals that do consist entirely of 0s and 2s, replacing all the 2s by 1s, and interpreting the sequence as abinaryrepresentation of a real number. In a formula,

$f{\bigg (}\sum _{k\in \mathbb {N} }a_{k}3^{-k}{\bigg )}=\sum _{k\in \mathbb {N} }{\frac {a_{k}}{2}}2^{-k}$where$\forall k\in \mathbb {N}:a_{k}\in \{0,2\}.$

For any numberyin [0,1], its binary representation can be translated into a ternary representation of a numberxin${\mathcal {C}}$by replacing all the 1s by 2s. With this,f(x) =yso thatyis in therangeoff.For instance ify=3/5= 0.100110011001...₂= 0.1001,we writex= 0.2002= 0.200220022002...₃=7/10.Consequently,fis surjective. However,fisnotinjective— the values for whichf(x) coincides are those at opposing ends of one of themiddle thirdsremoved. For instance, take

1/3= 0.02₃(which is a right limit point of${\mathcal {C}}$and a left limit point of the middle third [1/3,2/3]) and

2/3= 0.20₃(which is a left limit point of${\mathcal {C}}$and a right limit point of the middle third [1/3,2/3])

so

${\begin{array}{lcl}f{\bigl (}{}^{1}\!\!/\!_{3}{\bigr )}=f(0.0{\overline {2}}_{3})=0.0{\overline {1}}_{2}=\!\!&\!\!0.1_{2}\!\!&\!\!=0.1{\overline {0}}_{2}=f(0.2{\overline {0}}_{3})=f{\bigl (}{}^{2}\!\!/\!_{3}{\bigr )}.\\&\parallel \\&{}^{1}\!\!/\!_{2}\end{array}}$

Thus there are as many points in the Cantor set as there are in the interval [0, 1] (which has theuncountablecardinality${\mathfrak {c}}=2^{\aleph _{0}}$).However, the set of endpoints of the removed intervals is countable, so there must be uncountably many numbers in the Cantor set which are not interval endpoints. As noted above, one example of such a number is1/4,which can be written as 0.020202...₃= 0.02in ternary notation. In fact, given any$a\in [-1,1]$,there exist$x,y\in {\mathcal {C}}$such that$a=y-x$.This was first demonstrated bySteinhausin 1917, whoproved,via a geometric argument, the equivalent assertion that$\{(x,y)\in \mathbb {R} ^{2}\mid y=x+a\}\;\cap \;({\mathcal {C}}\times {\mathcal {C}})\neq \emptyset$for every$a\in [-1,1]$.Since this construction provides an injection from$[-1,1]$to${\mathcal {C}}\times {\mathcal {C}}$,we have$|{\mathcal {C}}\times {\mathcal {C}}|\geq |[-1,1]|={\mathfrak {c}}$as an immediatecorollary.Assuming that$|A\times A|=|A|$for any infinite set$A$(a statement shown to be equivalent to theaxiom of choiceby Tarski), this provides another demonstration that$|{\mathcal {C}}|={\mathfrak {c}}$.

The Cantor set contains as many points as the interval from which it is taken, yet itself contains no interval of nonzero length. Theirrational numbershave the same property, but the Cantor set has the additional property of beingclosed,so it is not evendensein any interval, unlike the irrational numbers which are dense in every interval.

It has beenconjecturedthat allalgebraicirrational numbers arenormal.Since members of the Cantor set are not normal, this would imply that all members of the Cantor set are either rational ortranscendental.

Self-similarity

The Cantor set is the prototype of afractal.It isself-similar,because it is equal to two copies of itself, if each copy is shrunk by a factor of 3 and translated. More precisely, the Cantor set is equal to the union of two functions, the left and right self-similarity transformations of itself,$T_{L}(x)=x/3$and$T_{R}(x)=(2+x)/3$,which leave the Cantor set invariant up tohomeomorphism:$T_{L}({\mathcal {C}})\cong T_{R}({\mathcal {C}})\cong {\mathcal {C}}=T_{L}({\mathcal {C}})\cup T_{R}({\mathcal {C}}).$

Repeatediterationof$T_{L}$and$T_{R}$can be visualized as an infinitebinary tree.That is, at each node of the tree, one may consider the subtree to the left or to the right. Taking the set$\{T_{L},T_{R}\}$together withfunction compositionforms amonoid,thedyadic monoid.

Theautomorphismsof the binary tree are its hyperbolic rotations, and are given by themodular group.Thus, the Cantor set is ahomogeneous spacein the sense that for any two points$x$and$y$in the Cantor set${\mathcal {C}}$,there exists a homeomorphism$h:{\mathcal {C}}\to {\mathcal {C}}$with$h(x)=y$.An explicit construction of$h$can be described more easily if we see the Cantor setas a product spaceof countably many copies of the discrete space$\{0,1\}$.Then the map$h:\{0,1\}^{\mathbb {N} }\to \{0,1\}^{\mathbb {N} }$defined by$h_{n}(u):=u_{n}+x_{n}+y_{n}\mod 2$is aninvolutivehomeomorphism exchanging$x$and$y$.

Conservation law

It has been found that some form of conservation law is always responsible behind scaling and self-similarity. In the case of Cantor set it can be seen that the$d_{f}$th moment (where$d_{f}=\ln(2)/\ln(3)$is thefractal dimension) of all the surviving intervals at any stage of the construction process is equal to a constant which is one in the case of the Cantor set. We know that there are$N=2^{n}$intervals of size$1/3^{n}$present in the system at the$n$th step of its construction. Then if we label the surviving intervals as$x_{1},x_{2},\ldots,x_{2^{n}}$then the$d_{f}$th moment is$x_{1}^{d_{f}}+x_{2}^{d_{f}}+\cdots +x_{2^{n}}^{d_{f}}=1$since$x_{1}=x_{2}=\cdots =x_{2^{n}}=1/3^{n}$.

TheHausdorff dimensionof the Cantor set is equal to ln(2)/ln(3) ≈ 0.631.

Topological and analytical properties

Although "the" Cantor set typically refers to the original, middle-thirds Cantor set described above, topologists often talk about "a" Cantor set, which means anytopological spacethat ishomeomorphic(topologically equivalent) to it.

As the above summation argument shows, the Cantor set is uncountable but hasLebesgue measure0. Since the Cantor set is thecomplementof aunionofopen sets,it itself is aclosedsubset of the reals, and therefore acomplete metric space.Since it is alsototally bounded,theHeine–Borel theoremsays that it must becompact.

For any point in the Cantor set and any arbitrarily smallneighborhoodof the point, there is some other number with a ternary numeral of only 0s and 2s, as well as numbers whose ternary numerals contain 1s. Hence, every point in the Cantor set is anaccumulation point(also called a cluster point or limit point) of the Cantor set, but none is aninterior point.A closed set in which every point is an accumulation point is also called aperfect setintopology,while a closed subset of the interval with no interior points isnowhere densein the interval.

Every point of the Cantor set is also an accumulation point of the complement of the Cantor set.

For any two points in the Cantor set, there will be some ternary digit where they differ — one will have 0 and the other 2. By splitting the Cantor set into "halves" depending on the value of this digit, one obtains a partition of the Cantor set into two closed sets that separate the original two points. In therelative topologyon the Cantor set, the points have been separated by aclopen set.Consequently, the Cantor set istotally disconnected.As a compact totally disconnectedHausdorff space,the Cantor set is an example of aStone space.

As a topological space, the Cantor set is naturally homeomorphic to theproductof countably many copies of the space$\{0,1\}$,where each copy carries thediscrete topology.This is the space of allsequencesin two digits

$2^{\mathbb {N} }=\{(x_{n})\mid x_{n}\in \{0,1\}{\text{ for }}n\in \mathbb {N} \},$

which can also be identified with the set of2-adic integers.Thebasisfor the open sets of theproduct topologyarecylinder sets;the homeomorphism maps these to thesubspace topologythat the Cantor set inherits from the natural topology on thereal line.This characterization of theCantor spaceas a product of compact spaces gives a second proof that Cantor space is compact, viaTychonoff's theorem.

From the above characterization, the Cantor set is homeomorphic to thep-adic integers,and, if one point is removed from it, to thep-adic numbers.

The Cantor set is a subset of the reals, which are ametric spacewith respect to theordinary distance metric;therefore the Cantor set itself is a metric space, by using that same metric. Alternatively, one can use thep-adic metricon$2^{\mathbb {N} }$:given two sequences$(x_{n}),(y_{n})\in 2^{\mathbb {N} }$,the distance between them is$d((x_{n}),(y_{n}))=2^{-k}$,where$k$is the smallest index such that$x_{k}\neq y_{k}$;if there is no such index, then the two sequences are the same, and one defines the distance to be zero. These two metrics generate the sametopologyon the Cantor set.

We have seen above that the Cantor set is a totally disconnectedperfectcompact metric space. Indeed, in a sense it is the only one: every nonempty totally disconnected perfect compact metric space is homeomorphic to the Cantor set. SeeCantor spacefor more on spaces homeomorphic to the Cantor set.

The Cantor set is sometimes regarded as "universal" in thecategoryofcompactmetric spaces, since any compact metric space is acontinuousimageof the Cantor set; however this construction is not unique and so the Cantor set is notuniversalin the precisecategoricalsense. The "universal" property has important applications infunctional analysis,where it is sometimes known as therepresentation theorem for compact metric spaces.

For anyintegerq≥ 2, the topology on thegroupG =Z_q^ω(the countable direct sum) is discrete. Although thePontrjagin dualΓ is alsoZ_q^ω,the topology of Γ is compact. One can see that Γ is totally disconnected and perfect - thus it is homeomorphic to the Cantor set. It is easiest to write out the homeomorphism explicitly in the caseq= 2. (See Rudin 1962 p 40.)

Measure and probability

The Cantor set can be seen as thecompact groupof binary sequences, and as such, it is endowed with a naturalHaar measure.When normalized so that the measure of the set is 1, it is a model of an infinite sequence of coin tosses. Furthermore, one can show that the usualLebesgue measureon the interval is an image of the Haar measure on the Cantor set, while the natural injection into the ternary set is a canonical example of asingular measure.It can also be shown that the Haar measure is an image of anyprobability,making the Cantor set a universal probability space in some ways.

InLebesgue measuretheory, the Cantor set is an example of a set which is uncountable and has zero measure.In contrast, the set has aHausdorff measureof 1 in its dimension of log 2 / log 3.

Cantor numbers

If we define a Cantor number as a member of the Cantor set, then

1. Every real number in [0, 2] is the sum of two Cantor numbers.
2. Between any two Cantor numbers there is a number that is not a Cantor number.

Descriptive set theory

The Cantor set is ameagre set(or a set of first category) as a subset of [0,1] (although not as a subset of itself, since it is aBaire space). The Cantor set thus demonstrates that notions of "size" in terms of cardinality, measure, and (Baire) category need not coincide. Like the set$\mathbb {Q} \cap [0,1]$,the Cantor set${\mathcal {C}}$is "small" in the sense that it is a null set (a set of measure zero) and it is a meagre subset of [0,1]. However, unlike$\mathbb {Q} \cap [0,1]$,which is countable and has a "small" cardinality,$\aleph _{0}$,the cardinality of${\mathcal {C}}$is the same as that of [0,1], the continuum${\mathfrak {c}}$,and is "large" in the sense of cardinality. In fact, it is also possible to construct a subset of [0,1] that is meagre but of positive measure and a subset that is non-meagre but of measure zero:By taking the countable union of "fat" Cantor sets${\mathcal {C}}^{(n)}$of measure$\lambda =(n-1)/n$(see Smith–Volterra–Cantor set below for the construction), we obtain a set${\textstyle {\mathcal {A}}:=\bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$which has a positive measure (equal to 1) but is meagre in [0,1], since each${\mathcal {C}}^{(n)}$is nowhere dense. Then consider the set${\textstyle {\mathcal {A}}^{\mathrm {c} }=[0,1]\setminus \bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$.Since${\mathcal {A}}\cup {\mathcal {A}}^{\mathrm {c} }=[0,1]$,${\mathcal {A}}^{\mathrm {c} }$cannot be meagre, but since$\mu ({\mathcal {A}})=1$,${\mathcal {A}}^{\mathrm {c} }$must have measure zero.

Variants

Radial plot of the first ten steps

Smith–Volterra–Cantor set

Main article:Smith–Volterra–Cantor set

Instead of repeatedly removing the middle third of every piece as in the Cantor set, we could also keep removing any other fixed percentage (other than 0% and 100%) from the middle. In the case where the middle8/10of the interval is removed, we get a remarkably accessible case — the set consists of all numbers in [0,1] that can be written as a decimal consisting entirely of 0s and 9s. If a fixed percentage is removed at each stage, then the limiting set will have measure zero, since the length of the remainder$(1-f)^{n}\to 0$as$n\to \infty$for any$f$such that$0<f\leq 1$.

On the other hand, "fat Cantor sets" of positive measure can be generated by removal of smaller fractions of the middle of the segment in each iteration. Thus, one can construct sets homeomorphic to the Cantor set that have positive Lebesgue measure while still being nowhere dense. If an interval of length$r^{n}$($r\leq 1/3$) is removed from the middle of each segment at thenth iteration, then the total length removed is${\textstyle \sum _{n=1}^{\infty }2^{n-1}r^{n}=r/(1-2r)}$,and the limiting set will have aLebesgue measureof$\lambda =(1-3r)/(1-2r)$.Thus, in a sense, the middle-thirds Cantor set is a limiting case with$r=1/3$.If$0<r<1/3$,then the remainder will have positive measure with$0<\lambda <1$.The case$r=1/4$is known as theSmith–Volterra–Cantor set,which has a Lebesgue measure of$1/2$.

Stochastic Cantor set

One can modify the construction of the Cantor set by dividing randomly instead of equally. Besides, to incorporate time we can divide only one of the available intervals at each step instead of dividing all the available intervals. In the case of stochastic triadic Cantor set the resulting process can be described by the following rate equation

${\frac {\partial c(x,t)}{\partial t}}=-{\frac {x^{2}}{2}}c(x,t)+2\int _{x}^{\infty }(y-x)c(y,t)\,dy,$

and for the stochastic dyadic Cantor set

${{\partial c(x,t)} \over {\partial t}}=-xc(x,t)+(1+p)\int _{x}^{\infty }c(y,t)\,dy,$

where$c(x,t)dx$is the number of intervals of size between$x$and$x+dx$.In the case of triadic Cantor set the fractal dimension is$0.5616$which is less than its deterministic counterpart$0.6309$.In the case of stochastic dyadic Cantor set the fractal dimension is$p$which is again less than that of its deterministic counterpart$\ln(1+p)/\ln 2$.In the case of stochastic dyadic Cantor set the solution for$c(x,t)$exhibitsdynamic scalingas its solution in the long-time limit is$t^{-(1+d_{f})}e^{-xt}$where the fractal dimension of the stochastic dyadic Cantor set$d_{f}=p$.In either case, like triadic Cantor set, the$d_{f}$th moment (${\textstyle \int x^{d_{f}}c(x,t)\,dx={\text{constant}}}$) of stochastic triadic and dyadic Cantor set too are conserved quantities.

Cantor dust

Cantor dustis a multi-dimensional version of the Cantor set. It can be formed by taking a finiteCartesian productof the Cantor set with itself, making it aCantor space.Like the Cantor set, Cantor dust haszero measure.

Cantor cubesrecursion progression towards Cantor dust

Cantor dust(2D)

Cantor dust(3D)

A different 2D analogue of the Cantor set is theSierpinski carpet,where a square is divided up into nine smaller squares, and the middle one removed. The remaining squares are then further divided into nine each and the middle removed, and so on ad infinitum.One 3D analogue of this is theMenger sponge.

Historical remarks

an image of the 2nd iteration of Cantor dust in two dimensions

an image of the 4th iteration of Cantor dust in two dimensions

Cantor introduced what we call today the Cantor ternary set${\mathcal {C}}$as an example "of aperfect point-set,which is not everywhere-dense in any interval, however small. "Cantor described${\mathcal {C}}$in terms of ternary expansions, as "the set of all real numbers given by the formula:$z=c_{1}/3+c_{2}/3^{2}+\cdots +c_{\nu }/3^{\nu }+\cdots$where the coefficients$c_{\nu }$arbitrarily take the two values 0 and 2, and the series can consist of a finite number or an infinite number of elements. "

A topological space$P$is perfect if all its points are limit points or, equivalently, if it coincides with itsderived set$P'$.Subsets of the real line, like${\mathcal {C}}$,can be seen as topological spaces under the induced subspace topology.

Cantor was led to the study of derived sets by his results on uniqueness oftrigonometric series.The latter did much to set him on the course for developing anabstract, general theory of infinite sets.

Benoit Mandelbrotwrote much on Cantor dusts and their relation tonatural fractalsandstatistical physics.He further reflected on the puzzling or even upsetting nature of such structures to those in the mathematics and physics community. InThe Fractal geometry of Nature,he described how "When I started on this topic in 1962, everyone was agreeing that Cantor dusts are at least as monstrous as theKochandPeano curves,"and added that" every self-respecting physicist was automatically turned off by a mention of Cantor, ready to run a mile from anyone claiming${\mathcal {C}}$to be interesting in science. "

See also

an image of the 6th iteration of Cantor dust in two dimensions

• The indicator function of the Cantor set
• Smith–Volterra–Cantor set
• Cantor function
• Cantor cube
• Antoine's necklace
• Koch snowflake
• Knaster–Kuratowski fan
• List of fractals by Hausdorff dimension
• Moser–de Bruijn sequence

  

  Column capital with pattern evocative of the Cantor set, but expressed in binary rather than ternary. Engraving of Île de Philae fromDescription d'Égypteby Jean-Baptiste Prosper Jollois and Édouard Devilliers, Imprimerie Impériale, Paris, 1809-1828

References

• Steen, Lynn Arthur;Seebach, J. Arthur Jr.(1995) [1978].Counterexamples in Topology(Doverreprint of 1978 ed.). Berlin, New York:Springer-Verlag.Example 29.ISBN978-0-486-68735-3.MR0507446.
• Wise, Gary L.; Hall, Eric B. (1993).Counterexamples in Probability and Real Analysis.New York:Oxford University Press.Chapter 1.ISBN0-19-507068-2.
• Falconer, K. J.(24 July 1986).Geometry of Fractal Sets.Cambridge Tracts in Mathematics.Cambridge University Press.ISBN0521337054.
• Mattila, Pertti (25 February 1999).Geometry of Sets and Measures in Euclidean Space: Fractals and rectifiability.Cambridge studies in advanced mathematics. Cambridge University Press.ISBN0521655951.
• Mattila, Pertti (2015).Fourier Analysis and Hausdorff Dimension.Cambridge studies in advanced mathematics. Cambridge University Press.ISBN9781316227619..
• Zygmund, A.(1958).Trigonometric Series, Vols. I and II.Cambridge University Press.

External links

• "Cantor set",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Cantor SetsandCantor Set and Functionatcut-the-knot
• Cantor Setat Platonic Realms