Capillary wave

"Rippled waves" redirects here. Not to be confused withRippled wave.For ripples in electricity, seeRipple (electrical).For other uses, seeRipple (disambiguation).

Capillary waves (ripples) in water

Ripples on Lifjord inØksnes Municipality,Norway

Capillary waves produced bydropletimpacts on the interface between water and air.

Acapillary waveis awavetraveling along thephase boundaryof a fluid, whosedynamicsandphase velocityare dominated by the effects ofsurface tension.

Capillary waves are common innature,and are often referred to asripples.Thewavelengthof capillary waves on water is typically less than a few centimeters, with aphase speedin excess of 0.2–0.3 meter/second.

A longer wavelength on a fluid interface will result ingravity–capillary waveswhich are influenced by both the effects of surface tension andgravity,as well as by fluidinertia.Ordinarygravity waveshave a still longer wavelength.

When generated by light wind in open water, a nautical name for them iscat's pawwaves. Light breezes which stir up such small ripples are also sometimes referred to as cat's paws. On the open ocean, much largerocean surface waves(seasandswells) may result from coalescence of smaller wind-caused ripple-waves.

Dispersion relation

Thedispersion relationdescribes the relationship betweenwavelengthandfrequencyin waves. Distinction can be made between pure capillary waves – fully dominated by the effects of surface tension – and gravity–capillary waves which are also affected by gravity.

Capillary waves, proper

The dispersion relation for capillary waves is

$\omega ^{2}={\frac {\sigma }{\rho +\rho '}}\,|k|^{3},$

where$\omega$is theangular frequency,$\sigma$thesurface tension,$\rho$thedensityof the heavier fluid,$\rho '$the density of the lighter fluid and$k$thewavenumber.Thewavelengthis $\lambda ={\frac {2\pi }{k}}.$ For the boundary between fluid and vacuum (free surface), the dispersion relation reduces to

$\omega ^{2}={\frac {\sigma }{\rho }}\,|k|^{3}.$

Gravity–capillary waves

Dispersion of gravity–capillary waves on the surface of deep water (zero mass density of upper layer,$\rho '=0$). Phase and group velocity divided by$\scriptstyle {\sqrt[{4}]{g\sigma /\rho }}$as a function of inverse relative wavelength$\scriptstyle {\frac {1}{\lambda }}{\sqrt {\sigma /(\rho g)}}$.
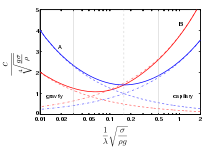
• Blue lines (A): phase velocity, Red lines (B): group velocity.
• Drawn lines: dispersion relation for gravity–capillary waves.
• Dashed lines: dispersion relation for deep-water gravity waves.
• Dash-dotted lines: dispersion relation valid for deep-water capillary waves.

When capillary waves are also affected substantially by gravity, they are called gravity–capillary waves. Their dispersion relation reads, for waves on the interface between two fluids of infinite depth:

$\omega ^{2}=|k|\left({\frac {\rho -\rho '}{\rho +\rho '}}g+{\frac {\sigma }{\rho +\rho '}}k^{2}\right),$

where$g$is the acceleration due togravity,$\rho$and$\rho '$are themass densityof the two fluids$(\rho >\rho ')$.The factor$(\rho -\rho ')/(\rho +\rho ')$in the first term is theAtwood number.

Gravity wave regime

Further information:Airy wave theory

For large wavelengths (small$k=2\pi /\lambda$), only the first term is relevant and one hasgravity waves. In this limit, the waves have agroup velocityhalf thephase velocity:following a single wave's crest in a group one can see the wave appearing at the back of the group, growing and finally disappearing at the front of the group.

Capillary wave regime

Shorter (large$k$) waves (e.g. 2 mm for the water–air interface), which are proper capillary waves, do the opposite: an individual wave appears at the front of the group, grows when moving towards the group center and finally disappears at the back of the group. Phase velocity is two thirds of group velocity in this limit.

Phase velocity minimum

Between these two limits is a point at which the dispersion caused by gravity cancels out the dispersion due to the capillary effect. At a certain wavelength, the group velocity equals the phase velocity, and there is no dispersion. At precisely this same wavelength, the phase velocity of gravity–capillary waves as a function of wavelength (or wave number) has a minimum. Waves with wavelengths much smaller than this critical wavelength$\lambda _{m}$are dominated by surface tension, and much above by gravity. The value of this wavelength and the associated minimum phase speed$c_{m}$are:

$\lambda _{m}=2\pi {\sqrt {\frac {\sigma }{(\rho -\rho ')g}}}\quad {\text{and}}\quad c_{m}={\sqrt {\frac {2{\sqrt {(\rho -\rho ')g\sigma }}}{\rho +\rho '}}}.$

For theair–waterinterface,$\lambda _{m}$is found to be 1.7 cm (0.67 in), and$c_{m}$is 0.23 m/s (0.75 ft/s).

If one drops a small stone or droplet into liquid, the waves then propagate outside an expanding circle of fluid at rest; this circle is acausticwhich corresponds to the minimal group velocity.

Derivation

AsRichard Feynmanput it, "[water waves] that are easily seen by everyone and which are usually used as an example of waves in elementary courses [...] are the worst possible example [...]; they have all the complications that waves can have."The derivation of the general dispersion relation is therefore quite involved.

There are three contributions to the energy, due to gravity, tosurface tension,and tohydrodynamics.The first two are potential energies, and responsible for the two terms inside the parenthesis, as is clear from the appearance of$g$and$\sigma$.For gravity, an assumption is made of the density of the fluids being constant (i.e., incompressibility), and likewise$g$(waves are not high enough for gravitation to change appreciably). For surface tension, the deviations from planarity (as measured by derivatives of the surface) are supposed to be small. For common waves both approximations are good enough.

The third contribution involves thekinetic energiesof the fluids. It is the most complicated and calls for ahydrodynamicframework. Incompressibility is again involved (which is satisfied if the speed of the waves is much less than the speed of sound in the media), together with the flow beingirrotational– the flow is thenpotential.These are typically also good approximations for common situations.

The resulting equation for the potential (which isLaplace equation) can be solved with the proper boundary conditions. On one hand, the velocity must vanish well below the surface (in the "deep water" case, which is the one we consider, otherwise a more involved result is obtained, seeOcean surface waves.) On the other, its vertical component must match the motion of the surface. This contribution ends up being responsible for the extra$k$outside the parenthesis, which causesallregimes to be dispersive, both at low values of$k$,and high ones (except around the one value at which the two dispersions cancel out.)

Dispersion relation for gravity–capillary waves on an interface between two semi–infinite fluid domains

Consider two fluid domains, separated by an interface with surface tension. The mean interface position is horizontal. It separates the upper from the lower fluid, both having a different constant mass density,$\rho$and$\rho '$for the lower and upper domain respectively. The fluid is assumed to beinviscidandincompressible,and the flow is assumed to beirrotational.Then the flows arepotential,and the velocity in the lower and upper layer can be obtained from$\nabla \phi$and$\nabla \phi '$,respectively. Here$\phi (x,y,z,t)$and$\phi '(x,y,z,t)$arevelocity potentials. Three contributions to the energy are involved: thepotential energy$V_{g}$due togravity,the potential energy$V_{st}$due to thesurface tensionand thekinetic energy$T$of the flow. The part$V_{g}$due to gravity is the simplest: integrating the potential energy density due to gravity,$\rho gz$(or$\rho 'gz$) from a reference height to the position of the surface,$z=\eta (x,y,t)$: $V_{\mathrm {g} }=\iint dx\,dy\;\int _{0}^{\eta }dz\;(\rho -\rho ')gz={\frac {1}{2}}(\rho -\rho ')g\iint dx\,dy\;\eta ^{2},$ assuming the mean interface position is at$z=0$. An increase in area of the surface causes a proportional increase of energy due to surface tension: $V_{\mathrm {st} }=\sigma \iint dx\,dy\;\left[{\sqrt {1+\left({\frac {\partial \eta }{\partial x}}\right)^{2}+\left({\frac {\partial \eta }{\partial y}}\right)^{2}}}-1\right]\approx {\frac {1}{2}}\sigma \iint dx\,dy\;\left[\left({\frac {\partial \eta }{\partial x}}\right)^{2}+\left({\frac {\partial \eta }{\partial y}}\right)^{2}\right],$ where the first equality is the area in this (Monge's) representation, and the second applies for small values of the derivatives (surfaces not too rough). The last contribution involves thekinetic energyof the fluid: $T={\frac {1}{2}}\iint dx\,dy\;\left[\int _{-\infty }^{\eta }dz\;\rho \,\left|\mathbf {\nabla } \Phi \right|^{2}+\int _{\eta }^{+\infty }dz\;\rho '\,\left|\mathbf {\nabla } \Phi '\right|^{2}\right].$ Use is made of the fluid being incompressible and its flow is irrotational (often, sensible approximations). As a result, both$\phi (x,y,z,t)$and$\phi '(x,y,z,t)$must satisfy theLaplace equation: $\nabla ^{2}\Phi =0$and$\nabla ^{2}\Phi '=0.$ These equations can be solved with the proper boundary conditions:$\phi$and$\phi '$must vanish well away from the surface (in the "deep water" case, which is the one we consider). UsingGreen's identity,and assuming the deviations of the surface elevation to be small (so thez–integrations may be approximated by integrating up to$z=0$instead of$z=\eta$), the kinetic energy can be written as: $T\approx {\frac {1}{2}}\iint dx\,dy\;\left[\rho \,\Phi \,{\frac {\partial \Phi }{\partial z}}\;-\;\rho '\,\Phi '\,{\frac {\partial \Phi '}{\partial z}}\right]_{{\text{at }}z=0}.$ To find the dispersion relation, it is sufficient to consider asinusoidalwave on the interface, propagating in thex–direction: $\eta =a\,\cos \,(kx-\omega t)=a\,\cos \,\theta,$ with amplitude$a$and wavephase$\theta =kx-\omega t$.The kinematic boundary condition at the interface, relating the potentials to the interface motion, is that the vertical velocity components must match the motion of the surface: ${\frac {\partial \Phi }{\partial z}}={\frac {\partial \eta }{\partial t}}$and${\frac {\partial \Phi '}{\partial z}}={\frac {\partial \eta }{\partial t}}$at$z=0$. To tackle the problem of finding the potentials, one may tryseparation of variables,when both fields can be expressed as: ${\begin{aligned}\Phi (x,y,z,t)&=+{\frac {1}{|k|}}{\text{e}}^{+|k|z}\,\omega a\,\sin \,\theta,\\\Phi '(x,y,z,t)&=-{\frac {1}{|k|}}{\text{e}}^{-|k|z}\,\omega a\,\sin \,\theta.\end{aligned}}$ Then the contributions to the wave energy, horizontally integrated over one wavelength$\lambda =2\pi /k$in thex–direction, and over a unit width in they–direction, become: ${\begin{aligned}V_{\text{g}}&={\frac {1}{4}}(\rho -\rho ')ga^{2}\lambda,\\V_{\text{st}}&={\frac {1}{4}}\sigma k^{2}a^{2}\lambda,\\T&={\frac {1}{4}}(\rho +\rho '){\frac {\omega ^{2}}{|k|}}a^{2}\lambda.\end{aligned}}$ The dispersion relation can now be obtained from theLagrangian$L=T-V$,with$V$the sum of the potential energies by gravity$V_{g}$and surface tension$V_{st}$: $L={\frac {1}{4}}\left[(\rho +\rho '){\frac {\omega ^{2}}{|k|}}-(\rho -\rho ')g-\sigma k^{2}\right]a^{2}\lambda.$ For sinusoidal waves and linear wave theory, thephase–averaged Lagrangianis always of the form$L=D(\omega,k)a^{2}$,so that variation with respect to the only free parameter,$a$,gives the dispersion relation$D(\omega,k)=0$.In our case$D(\omega,k)$is just the expression in the square brackets, so that the dispersion relation is: $\omega ^{2}=|k|\left({\frac {\rho -\rho '}{\rho +\rho '}}\,g+{\frac {\sigma }{\rho +\rho '}}\,k^{2}\right),$ the same as above. As a result, the average wave energy per unit horizontal area,$(T+V)/\lambda$,is: ${\bar {E}}={\frac {1}{2}}\,\left[(\rho -\rho ')\,g+\sigma k^{2}\right]\,a^{2}.$ As usual for linear wave motions, the potential and kinetic energy are equal (equipartitionholds):$T=V$.

See also

• Capillary action
• Dispersion (water waves)
• Fluid pipe
• Ocean surface wave
• Thermal capillary wave
• Two-phase flow
• Wave-formed ripple

Gallery

• 
  Ripples on water created bywater striders
• 
  Light breeze ripples in the surface water of a lake

References

• Longuet-Higgins, M. S.(1963). "The generation of capillary waves by steep gravity waves".Journal of Fluid Mechanics.16(1): 138–159.Bibcode:1963JFM....16..138L.doi:10.1017/S0022112063000641.ISSN1469-7645.S2CID119740891.
• Lamb, H.(1994).Hydrodynamics(6th ed.). Cambridge University Press.ISBN978-0-521-45868-9.
• Phillips, O. M.(1977).The dynamics of the upper ocean(2nd ed.). Cambridge University Press.ISBN0-521-29801-6.
• Dingemans, M. W. (1997).Water wave propagation over uneven bottoms.Advanced Series on Ocean Engineering. Vol. 13. World Scientific, Singapore. pp. 2 Parts, 967 pages.ISBN981-02-0427-2.
• Safran, Samuel (1994).Statistical thermodynamics of surfaces, interfaces, and membranes.Addison-Wesley.
• Tufillaro, N. B.; Ramshankar, R.; Gollub, J. P. (1989)."Order-disorder transition in capillary ripples".Physical Review Letters.62(4): 422–425.Bibcode:1989PhRvL..62..422T.doi:10.1103/PhysRevLett.62.422.PMID10040229.

External links

• Capillary waves entry at sklogwiki