Limit (category theory)

Incategory theory,a branch ofmathematics,the abstract notion of alimitcaptures the essential properties of universal constructions such asproducts,pullbacksandinverse limits.Thedual notionof acolimitgeneralizes constructions such asdisjoint unions,direct sums,coproducts,pushoutsanddirect limits.

Limits and colimits, like the strongly related notions ofuniversal propertiesandadjoint functors,exist at a high level of abstraction. In order to understand them, it is helpful to first study the specific examples these concepts are meant to generalize.

Definition

Limits and colimits in acategory $C$ are defined by means of diagrams in $C$ .Formally, adiagramof shape $J$ in $C$ is afunctorfrom $J$ to $C$ :

F:J\to C.

The category $J$ is thought of as anindex category,and the diagram $F$ is thought of as indexing a collection of objects andmorphismsin $C$ patterned on $J$ .

One is most often interested in the case where the category $J$ is asmallor evenfinitecategory. A diagram is said to besmallorfinitewhenever $J$ is.

Limits

Let $F:J\to C$ be a diagram of shape $J$ in a category $C$ .Aconeto $F$ is an object $N$ of $C$ together with a family $\psi _{X}:N\to F(X)$ of morphisms indexed by the objects $X$ of $J$ ,such that for every morphism $f:X\to Y$ in $J$ ,we have $F(f)\circ \psi _{X}=\psi _{Y}$ .

Alimitof the diagram $F:J\to C$ is a cone $(L,\phi )$ to $F$ such that for every cone $(N,\psi )$ to $F$ there exists auniquemorphism $u:N\to L$ such that $\phi _{X}\circ u=\psi _{X}$ for all $X$ in $J$ .

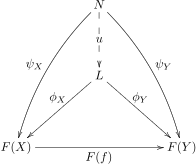
One says that the cone $(N,\psi )$ factors through the cone $(L,\phi )$ with the unique factorization $u$ .The morphism $u$ is sometimes called themediating morphism.

Limits are also referred to asuniversal cones,since they are characterized by auniversal property(see below for more information). As with every universal property, the above definition describes a balanced state of generality: The limit object $L$ has to be general enough to allow any cone to factor through it; on the other hand, $L$ has to be sufficiently specific, so that onlyonesuch factorization is possible for every cone.

Limits may also be characterized asterminal objectsin thecategory of conestoF.

It is possible that a diagram does not have a limit at all. However, if a diagram does have a limit then this limit is essentially unique: it is uniqueup toa uniqueisomorphism.For this reason one often speaks ofthelimit ofF.

Colimits

Thedual notionsof limits and cones are colimits and co-cones. Although it is straightforward to obtain the definitions of these by inverting all morphisms in the above definitions, we will explicitly state them here:

Aco-coneof a diagram $F:J\to C$ is an object $N$ of $C$ together with a family of morphisms

\psi _{X}:F(X)\to N

for every object $X$ of $J$ ,such that for every morphism $f:X\to Y$ in $J$ ,we have $\psi _{Y}\circ F(f)=\psi _{X}$ .

Acolimitof a diagram $F:J\to C$ is a co-cone $(L,\phi )$ of $F$ such that for any other co-cone $(N,\psi )$ of $F$ there exists a unique morphism $u:L\to N$ such that $u\circ \phi _{X}=\psi _{X}$ for all $X$ in $J$ .

Colimits are also referred to asuniversal co-cones.They can be characterized asinitial objectsin thecategory of co-conesfrom $F$ .

As with limits, if a diagram $F$ has a colimit then this colimit is unique up to a unique isomorphism.

Variations

Limits and colimits can also be defined for collections of objects and morphisms without the use of diagrams. The definitions are the same (note that in definitions above we never needed to use composition of morphisms in $J$ ). This variation, however, adds no new information. Any collection of objects and morphisms defines a (possibly large)directed graph $G$ .If we let $J$ be thefree categorygenerated by $G$ ,there is a universal diagram $F:J\to C$ whose image contains $G$ .The limit (or colimit) of this diagram is the same as the limit (or colimit) of the original collection of objects and morphisms.

Weak limitandweak colimitsare defined like limits and colimits, except that the uniqueness property of the mediating morphism is dropped.

Examples

Limits

The definition of limits is general enough to subsume several constructions useful in practical settings. In the following we will consider the limit (L,φ) of a diagramF:J→C.

Terminal objects.IfJis the empty category there is only one diagram of shapeJ:the empty one (similar to theempty functionin set theory). A cone to the empty diagram is essentially just an object ofC.The limit ofFis any object that is uniquely factored through by every other object. This is just the definition of aterminal object.
Products.IfJis adiscrete categorythen a diagramFis essentially nothing but afamilyof objects ofC,indexed byJ.The limitLofFis called theproductof these objects. The coneφconsists of a family of morphismsφ_X:L→F(X) called theprojectionsof the product. In thecategory of sets,for instance, the products are given byCartesian productsand the projections are just the natural projections onto the various factors.
- Powers.A special case of a product is when the diagramFis aconstant functorto an objectXofC.The limit of this diagram is called theJ^thpowerofXand denotedX^J.
Equalizers.IfJis a category with two objects and two parallel morphisms from one object to the other, then a diagram of shapeJis a pair of parallel morphisms inC.The limitLof such a diagram is called anequalizerof those morphisms.
- Kernels.Akernelis a special case of an equalizer where one of the morphisms is azero morphism.
Pullbacks.LetFbe a diagram that picks out three objectsX,Y,andZinC,where the only non-identity morphisms aref:X→Zandg:Y→Z.The limitLofFis called apullbackor afiber product.It can nicely be visualized as acommutative square:

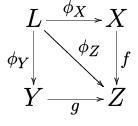
Inverse limits.LetJbe adirected set(considered as a small category by adding arrowsi→jif and only ifi≥j) and letF:J^op→Cbe a diagram. The limit ofFis called aninverse limitorprojective limit.
IfJ=1,the category with a single object and morphism, then a diagram of shapeJis essentially just an objectXofC.A cone to an objectXis just a morphism with codomainX.A morphismf:Y→Xis a limit of the diagramXif and only iffis anisomorphism.More generally, ifJis any category with aninitial objecti,then any diagram of shapeJhas a limit, namely any object isomorphic toF(i). Such an isomorphism uniquely determines a universal cone toF.
Topological limits.Limits of functions are a special case oflimits of filters,which are related to categorical limits as follows. Given atopological spaceX,denote byFthe set of filters onX,x∈Xa point,V(x) ∈Ftheneighborhood filterofx,A∈Fa particular filter and $F_{x,A}=\{G\in F\mid V(x)\cup A\subset G\}$ the set of filters finer thanAand that converge tox.The filtersFare given a small and thin category structure by adding an arrowA→Bif and only ifA⊆B.The injection $I_{x,A}:F_{x,A}\to F$ becomes a functor and the following equivalence holds:

xis a topological limit ofAif and only ifAis a categorical limit of

I_{x,A}

Colimits

Examples of colimits are given by the dual versions of the examples above:

Initial objectsare colimits of empty diagrams.
Coproductsare colimits of diagrams indexed by discrete categories.
- Copowersare colimits of constant diagrams from discrete categories.
Coequalizersare colimits of a parallel pair of morphisms.
- Cokernelsare coequalizers of a morphism and a parallel zero morphism.
Pushoutsare colimits of a pair of morphisms with common domain.
Direct limitsare colimits of diagrams indexed by directed sets.

Properties

Existence of limits

A given diagramF:J→Cmay or may not have a limit (or colimit) inC.Indeed, there may not even be a cone toF,let alone a universal cone.

A categoryCis said tohave limits of shapeJif every diagram of shapeJhas a limit inC.Specifically, a categoryCis said to

have productsif it has limits of shapeJfor everysmalldiscrete categoryJ(it need not have large products),
have equalizersif it has limits of shape $\bullet \rightrightarrows \bullet$ (i.e. every parallel pair of morphisms has an equalizer),
have pullbacksif it has limits of shape $\bullet \rightarrow \bullet \leftarrow \bullet$ (i.e. every pair of morphisms with common codomain has a pullback).

Acomplete categoryis a category that has all small limits (i.e. all limits of shapeJfor every small categoryJ).

One can also make the dual definitions. A categoryhas colimits of shapeJif every diagram of shapeJhas a colimit inC.Acocomplete categoryis one that has all small colimits.

Theexistence theorem for limitsstates that if a categoryChas equalizers and all products indexed by the classes Ob(J) and Hom(J), thenChas all limits of shapeJ.^[1]^{: §V.2 Thm.1}In this case, the limit of a diagramF:J→Ccan be constructed as the equalizer of the two morphisms^[1]^{: §V.2 Thm.2}

s,t:\prod _{i\in \operatorname {Ob} (J)}F(i)\rightrightarrows \prod _{f\in \operatorname {Hom} (J)}F(\operatorname {cod} (f))

given (in component form) by

{\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatorname {dom} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}\\t&={\bigl (}\pi _{\operatorname {cod} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}.\end{aligned}}

There is a dualexistence theorem for colimitsin terms of coequalizers and coproducts. Both of these theorems give sufficient and necessary conditions for the existence of all (co)limits of shapeJ.

Universal property

Limits and colimits are important special cases ofuniversal constructions.

LetCbe a category and letJbe a small index category. Thefunctor categoryC^Jmay be thought of as the category of all diagrams of shapeJinC.Thediagonal functor

\Delta:{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}

is the functor that maps each objectNinCto the constant functor Δ(N):J→CtoN.That is, Δ(N)(X) =Nfor each objectXinJand Δ(N)(f) = id_Nfor each morphismfinJ.

Given a diagramF:J→C(thought of as an object inC^J), anatural transformationψ:Δ(N) →F(which is just a morphism in the categoryC^J) is the same thing as a cone fromNtoF.To see this, first note that Δ(N)(X) =Nfor all X implies that the components ofψare morphismsψ_X:N→F(X), which all share the domainN.Moreover, the requirement that the cone's diagrams commute is true simply because thisψis a natural transformation. (Dually, a natural transformationψ:F→ Δ(N) is the same thing as a co-cone fromFtoN.)

Therefore, the definitions of limits and colimits can then be restated in the form:

A limit ofFis a universal morphism from Δ toF.
A colimit ofFis a universal morphism fromFto Δ.

Adjunctions

Like all universal constructions, the formation of limits and colimits is functorial in nature. In other words, if every diagram of shapeJhas a limit inC(forJsmall) there exists alimit functor

\lim:{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}

which assigns each diagram its limit and eachnatural transformationη:F→Gthe unique morphism lim η: limF→ limGcommuting with the corresponding universal cones. This functor isright adjointto the diagonal functor Δ:C→C^J. This adjunction gives a bijection between the set of all morphisms fromNto limFand the set of all cones fromNtoF

\operatorname {Hom} (N,\lim F)\cong \operatorname {Cone} (N,F)

which is natural in the variablesNandF.The counit of this adjunction is simply the universal cone from limFtoF.If the index categoryJisconnected(and nonempty) then the unit of the adjunction is an isomorphism so that lim is a left inverse of Δ. This fails ifJis not connected. For example, ifJis a discrete category, the components of the unit are thediagonal morphismsδ:N→N^J.

Dually, if every diagram of shapeJhas a colimit inC(forJsmall) there exists acolimit functor

\operatorname {colim}:{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}

which assigns each diagram its colimit. This functor isleft adjointto the diagonal functor Δ:C→C^J,and one has a natural isomorphism

\operatorname {Hom} (\operatorname {colim} F,N)\cong \operatorname {Cocone} (F,N).

The unit of this adjunction is the universal cocone fromFto colimF.IfJis connected (and nonempty) then the counit is an isomorphism, so that colim is a left inverse of Δ.

Note that both the limit and the colimit functors arecovariantfunctors.

As representations of functors

One can useHom functorsto relate limits and colimits in a categoryCto limits inSet,thecategory of sets.This follows, in part, from the fact the covariant Hom functor Hom(N,–):C→Setpreserves all limitsinC.By duality, the contravariant Hom functor must take colimits to limits.

If a diagramF:J→Chas a limit inC,denoted by limF,there is acanonical isomorphism

\operatorname {Hom} (N,\lim F)\cong \lim \operatorname {Hom} (N,F-)

which is natural in the variableN.Here the functor Hom(N,F–) is the composition of the Hom functor Hom(N,–) withF.This isomorphism is the unique one which respects the limiting cones.

One can use the above relationship to define the limit ofFinC.The first step is to observe that the limit of the functor Hom(N,F–) can be identified with the set of all cones fromNtoF:

\lim \operatorname {Hom} (N,F-)=\operatorname {Cone} (N,F).

The limiting cone is given by the family of maps π_X:Cone(N,F) → Hom(N,FX) where $π$ _X(ψ) =ψ_X.If one is given an objectLofCtogether with anatural isomorphismΦ:Hom(L,–) → Cone(–,F), the objectLwill be a limit ofFwith the limiting cone given byΦ_L(id_L). In fancy language, this amounts to saying that a limit ofFis arepresentationof the functor Cone(–,F):C→Set.

Dually, if a diagramF:J→Chas a colimit inC,denoted colimF,there is a unique canonical isomorphism

\operatorname {Hom} (\operatorname {colim} F,N)\cong \lim \operatorname {Hom} (F-,N)

which is natural in the variableNand respects the colimiting cones. Identifying the limit of Hom(F–,N) with the set Cocone(F,N), this relationship can be used to define the colimit of the diagramFas a representation of the functor Cocone(F,–).

Interchange of limits and colimits of sets

LetIbe a finite category andJbe a smallfiltered category.For anybifunctor

F:I\times J\to \mathbf {Set},

there is anatural isomorphism

\operatorname {colim} \limits _{J}\lim _{I}F(i,j)\rightarrow \lim _{I}\operatorname {colim} \limits _{J}F(i,j).

In words, filtered colimits inSetcommute with finite limits. It also holds that small colimits commute with small limits.^[2]

Functors and limits

IfF:J→Cis a diagram inCandG:C→Dis afunctorthen by composition (recall that a diagram is just a functor) one obtains a diagramGF:J→D.A natural question is then:

“How are the limits ofGFrelated to those ofF?”

Preservation of limits

A functorG:C→Dinduces a map from Cone(F) to Cone(GF): ifΨis a cone fromNtoFthenGΨis a cone fromGNtoGF.The functorGis said topreserve the limits ofFif (GL,Gφ) is a limit ofGFwhenever (L,φ) is a limit ofF.(Note that if the limit ofFdoes not exist, thenGvacuouslypreserves the limits ofF.)

A functorGis said topreserve all limits of shapeJif it preserves the limits of all diagramsF:J→C.For example, one can say thatGpreserves products, equalizers, pullbacks, etc. Acontinuous functoris one that preserves allsmalllimits.

One can make analogous definitions for colimits. For instance, a functorGpreserves the colimits ofFifG(L,φ) is a colimit ofGFwhenever (L,φ) is a colimit ofF.Acocontinuous functoris one that preserves allsmallcolimits.

IfCis acomplete category,then, by the above existence theorem for limits, a functorG:C→Dis continuous if and only if it preserves (small) products and equalizers. Dually,Gis cocontinuous if and only if it preserves (small) coproducts and coequalizers.

An important property ofadjoint functorsis that every right adjoint functor is continuous and every left adjoint functor is cocontinuous. Since adjoint functors exist in abundance, this gives numerous examples of continuous and cocontinuous functors.

For a given diagramF:J→Cand functorG:C→D,if bothFandGFhave specified limits there is a unique canonical morphism

\tau _{F}:G\lim F\to \lim GF

which respects the corresponding limit cones. The functorGpreserves the limits ofFif and only if this map is an isomorphism. If the categoriesCandDhave all limits of shapeJthen lim is a functor and the morphisms τ_Fform the components of anatural transformation

\tau:G\lim \to \lim G^{J}.

The functorGpreserves all limits of shapeJif and only if τ is a natural isomorphism. In this sense, the functorGcan be said tocommute with limits(up toa canonical natural isomorphism).

Preservation of limits and colimits is a concept that only applies tocovariantfunctors. Forcontravariant functorsthe corresponding notions would be a functor that takes colimits to limits, or one that takes limits to colimits.

Lifting of limits

A functorG:C→Dis said tolift limitsfor a diagramF:J→Cif whenever (L,φ) is a limit ofGFthere exists a limit (L′,φ′) ofFsuch thatG(L′,φ′) = (L,φ). A functorGlifts limits of shapeJif it lifts limits for all diagrams of shapeJ.One can therefore talk about lifting products, equalizers, pullbacks, etc. Finally, one says thatGlifts limitsif it lifts all limits. There are dual definitions for the lifting of colimits.

A functorGlifts limits uniquelyfor a diagramFif there is a unique preimage cone (L′,φ′) such that (L′,φ′) is a limit ofFandG(L′,φ′) = (L,φ). One can show thatGlifts limits uniquely if and only if it lifts limits and isamnestic.

Lifting of limits is clearly related to preservation of limits. IfGlifts limits for a diagramFandGFhas a limit, thenFalso has a limit andGpreserves the limits ofF.It follows that:

IfGlifts limits of all shapeJandDhas all limits of shapeJ,thenCalso has all limits of shapeJandGpreserves these limits.
IfGlifts all small limits andDis complete, thenCis also complete andGis continuous.

The dual statements for colimits are equally valid.

Creation and reflection of limits

LetF:J→Cbe a diagram. A functorG:C→Dis said to

create limitsforFif whenever (L,φ) is a limit ofGFthere exists a unique cone (L′,φ′) toFsuch thatG(L′,φ′) = (L,φ), and furthermore, this cone is a limit ofF.
reflect limitsforFif each cone toFwhose image underGis a limit ofGFis already a limit ofF.

Dually, one can define creation and reflection of colimits.

The following statements are easily seen to be equivalent:

The functorGcreates limits.
The functorGlifts limits uniquely and reflects limits.

There are examples of functors which lift limits uniquely but neither create nor reflect them.

Examples

Everyrepresentable functorC→Setpreserves limits (but not necessarily colimits). In particular, for any objectAofC,this is true of the covariantHom functorHom(A,–):C→Set.
Theforgetful functorU:Grp→Setcreates (and preserves) all small limits andfiltered colimits;however,Udoes not preserve coproducts. This situation is typical of algebraic forgetful functors.
Thefree functorF:Set→Grp(which assigns to every setSthefree groupoverS) is left adjoint to forgetful functorUand is, therefore, cocontinuous. This explains why thefree productof two free groupsGandHis the free group generated by thedisjoint unionof the generators ofGandH.
The inclusion functorAb→Grpcreates limits but does not preserve coproducts (the coproduct of two abelian groups being thedirect sum).
The forgetful functorTop→Setlifts limits and colimits uniquely but creates neither.
LetMet_cbe the category ofmetric spaceswithcontinuous functionsfor morphisms. The forgetful functorMet_c→Setlifts finite limits but does not lift them uniquely.

A note on terminology

Older terminology referred to limits as "inverse limits" or "projective limits", and to colimits as "direct limits" or "inductive limits". This has been the source of a lot of confusion.

There are several ways to remember the modern terminology. First of all,

cokernels,
coproducts,
coequalizers, and
codomains

are types of colimits, whereas

kernels,
products
equalizers, and
domains

are types of limits. Second, the prefix "co" implies "first variable of the $\operatorname {Hom}$ ".Terms like" cohomology "and" cofibration "all have a slightly stronger association with the first variable, i.e., the contravariant variable, of the $\operatorname {Hom}$ bifunctor.

References

^^a ^bMac Lane, Saunders(1998).Categories for the Working Mathematician.Graduate Texts in Mathematics.Vol. 5 (2nd ed.).Springer-Verlag.ISBN 0-387-98403-8.Zbl 0906.18001.
^commutativity of limits and colimitsat thenLab

External links

Interactive Web pagewhich generates examples of limits and colimits in the category of finite sets. Written byJocelyn Paine.
Limitat thenLab

[Mac_Lane-1] Mac Lane, Saunders(1998).Categories for the Working Mathematician.Graduate Texts in Mathematics.Vol. 5 (2nd ed.).Springer-Verlag.ISBN 0-387-98403-8.Zbl 0906.18001.

[2] utativity of limits and colimitsat thenLab

[1]

[2]

Limit (category theory)

Definition

Limits

Colimits

Variations

Examples

Limits

Colimits

Properties

Existence of limits

Universal property

Adjunctions

As representations of functors

Interchange of limits and colimits of sets

Functors and limits

Preservation of limits

Lifting of limits

Creation and reflection of limits

Examples

A note on terminology

See also

References

Further reading

External links