Commutative property

"Commutative" redirects here. For other uses, seeCommutative (disambiguation).

Commutative property

Type	Property
Field	Algebra
Statement	Abinary operationiscommutativeif changing the order of theoperandsdoes not change the result.
Symbolic statement	$x*y=y*x\quad \forall x,y\in S.$

Inmathematics,abinary operationiscommutativeif changing the order of theoperandsdoes not change the result. It is a fundamental property of many binary operations, and manymathematical proofsdepend on it. Perhaps most familiar as a property of arithmetic, e.g."3 + 4 = 4 + 3"or"2 × 5 = 5 × 2",the property can also be used in more advanced settings. The name is needed because there are operations, such asdivisionandsubtraction,that do not have it (for example,"3 − 5 ≠ 5 − 3"); such operations arenotcommutative, and so are referred to asnoncommutative operations.The idea that simple operations, such as themultiplicationandadditionof numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized.A similar property exists forbinary relations;a binary relation is said to besymmetricif the relation applies regardless of the order of its operands; for example,equalityis symmetric as two equal mathematical objects are equal regardless of their order.

Mathematical definitions

Abinary operation$*$on asetSis calledcommutativeif $$x*y=y*x\qquad {\mbox{for all }}x,y\in S.$$ In other words, an operation is commutative if every two elements commute. An operation that does not satisfy the above property is callednoncommutative.

One says thatxcommuteswithyor thatxandycommuteunder$*$if $$x*y=y*x.$$ That is, a specific pair of elements may commute even if the operation is (strictly) noncommutative.

Examples

The cumulation of apples, which can be seen as an addition of natural numbers, is commutative.

Commutative operations

The addition of vectors is commutative, because${\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}.$

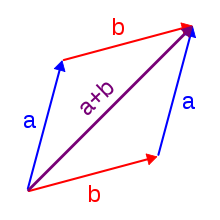
• Additionandmultiplicationare commutative in mostnumber systems,and, in particular, betweennatural numbers,integers,rational numbers,real numbersandcomplex numbers.This is also true in everyfield.
• Addition is commutative in everyvector spaceand in everyalgebra.
• Unionandintersectionare commutative operations onsets.
• "And"and"or"are commutativelogical operations.

Noncommutative operations

Division, subtraction, and exponentiation

See also:Equation xy = yx

Divisionis noncommutative, since$1\div 2\neq 2\div 1$.

Subtractionis noncommutative, since$0-1\neq 1-0$.However it is classified more precisely asanti-commutative,since$0-1=-(1-0)$.

Exponentiationis noncommutative, since$2^{3}\neq 3^{2}$.This property leads to two different "inverse" operations of exponentiation (namely, thenth-rootoperation and thelogarithmoperation), whereas multiplication only has one inverse operation.

Truth functions

Sometruth functionsare noncommutative, since thetruth tablesfor the functions are different when one changes the order of the operands. For example, the truth tables for(A ⇒ B) = (¬A ∨ B)and(B ⇒ A) = (A ∨ ¬B)are

A	B	A ⇒ B	B ⇒ A
F	F	T	T
F	T	T	F
T	F	F	T
T	T	T	T

Function composition of linear functions

Function compositionoflinear functionsfrom thereal numbersto the real numbers is almost always noncommutative. For example, let$f(x)=2x+1$and$g(x)=3x+7$.Then $$(f\circ g)(x)=f(g(x))=2(3x+7)+1=6x+15$$ and $$(g\circ f)(x)=g(f(x))=3(2x+1)+7=6x+10$$ This also applies more generally forlinearandaffine transformationsfrom avector spaceto itself (see below for the Matrix representation).

Matrix multiplication

Matrix multiplicationofsquare matricesis almost always noncommutative, for example: $${\begin{bmatrix}0&2\\0&1\end{bmatrix}}={\begin{bmatrix}1&1\\0&1\end{bmatrix}}{\begin{bmatrix}0&1\\0&1\end{bmatrix}}\neq {\begin{bmatrix}0&1\\0&1\end{bmatrix}}{\begin{bmatrix}1&1\\0&1\end{bmatrix}}={\begin{bmatrix}0&1\\0&1\end{bmatrix}}$$

Vector product

The vector product (orcross product) of two vectors in three dimensions isanti-commutative;i.e.,b×a= −(a×b).

History and etymology

The first known use of the term was in a French Journal published in 1814

Records of the implicit use of the commutative property go back to ancient times. TheEgyptiansused the commutative property ofmultiplicationto simplify computingproducts.Euclidis known to have assumed the commutative property of multiplication in his bookElements.Formal uses of the commutative property arose in the late 18th and early 19th centuries, when mathematicians began to work on a theory of functions. Today the commutative property is a well-known and basic property used in most branches of mathematics.

The first recorded use of the termcommutativewas in a memoir byFrançois Servoisin 1814,which used the wordcommutativeswhen describing functions that have what is now called the commutative property.Commutativeis the feminine form of the French adjectivecommutatif,which is derived from the French nouncommutationand the French verbcommuter,meaning "to exchange" or "to switch", a cognate ofto commute.The term then appeared in English in 1838.inDuncan Gregory's article entitled "On the real nature of symbolical algebra" published in 1840 in theTransactions of the Royal Society of Edinburgh.

Propositional logic

Rule of replacement

In truth-functional propositional logic,commutation,orcommutativityrefer to twovalidrules of replacement.The rules allow one to transposepropositional variableswithinlogical expressionsinlogical proofs.The rules are: $$(P\lor Q)\Leftrightarrow (Q\lor P)$$ and $$(P\land Q)\Leftrightarrow (Q\land P)$$ where "$\Leftrightarrow$"is ametalogicalsymbolrepresenting "can be replaced in aproofwith ".

Truth functional connectives

Commutativityis a property of somelogical connectivesof truth functionalpropositional logic.The followinglogical equivalencesdemonstrate that commutativity is a property of particular connectives. The following are truth-functionaltautologies.

Commutativity of conjunction

$(P\land Q)\leftrightarrow (Q\land P)$

Commutativity of disjunction

$(P\lor Q)\leftrightarrow (Q\lor P)$

Commutativity of implication (also called the law of permutation)

${\big (}P\to (Q\to R){\big )}\leftrightarrow {\big (}Q\to (P\to R){\big )}$

Commutativity of equivalence (also called the complete commutative law of equivalence)

$(P\leftrightarrow Q)\leftrightarrow (Q\leftrightarrow P)$

Set theory

Ingroupandset theory,many algebraic structures are called commutative when certain operands satisfy the commutative property. In higher branches of mathematics, such asanalysisandlinear algebrathe commutativity of well-known operations (such asadditionandmultiplicationon real and complex numbers) is often used (or implicitly assumed) in proofs.

Mathematical structures and commutativity

• Acommutative semigroupis a set endowed with a total,associativeand commutative operation.
• If the operation additionally has anidentity element,we have acommutative monoid
• Anabelian group,orcommutative groupis agroupwhose group operation is commutative.
• Acommutative ringis aringwhosemultiplicationis commutative. (Addition in a ring is always commutative.)
• In afieldboth addition and multiplication are commutative.

Related properties

Associativity

Main article:Associative property

The associative property is closely related to the commutative property. The associative property of an expression containing two or more occurrences of the same operator states that the order operations are performed in does not affect the final result, as long as the order of terms does not change. In contrast, the commutative property states that the order of the terms does not affect the final result.

Most commutative operations encountered in practice are also associative. However, commutativity does not imply associativity. A counterexample is the function $$f(x,y)={\frac {x+y}{2}},$$ which is clearly commutative (interchangingxandydoes not affect the result), but it is not associative (since, for example,$f(-4,f(0,+4))=-1$but$f(f(-4,0),+4)=+1$). More such examples may be found incommutative non-associative magmas.Furthermore, associativity does not imply commutativity either – for example multiplication ofquaternionsor ofmatricesis always associative but not always commutative.

Distributive

Main article:Distributive property

Symmetry

Graph showing the symmetry of the addition function

Some forms ofsymmetrycan be directly linked to commutativity. When a commutative operation is written as abinary function$z=f(x,y),$then this function is called asymmetric function,and itsgraphinthree-dimensional spaceis symmetric across the plane$y=x$.For example, if the functionfis defined as$f(x,y)=x+y$then$f$is a symmetric function.

For relations, asymmetric relationis analogous to a commutative operation, in that if a relationRis symmetric, then$aRb\Leftrightarrow bRa$.

Non-commuting operators in quantum mechanics

Main article:Canonical commutation relation

Inquantum mechanicsas formulated bySchrödinger,physical variables are represented bylinear operatorssuch as$x$(meaning multiply by$x$), and${\textstyle {\frac {d}{dx}}}$.These two operators do not commute as may be seen by considering the effect of theircompositions${\textstyle x{\frac {d}{dx}}}$and${\textstyle {\frac {d}{dx}}x}$(also called products of operators) on a one-dimensionalwave function$\psi (x)$: $$x\cdot {\mathrm {d} \over \mathrm {d} x}\psi =x\cdot \psi '\ \neq \ \psi +x\cdot \psi '={\mathrm {d} \over \mathrm {d} x}\left(x\cdot \psi \right)$$

According to theuncertainty principleofHeisenberg,if the two operators representing a pair of variables do not commute, then that pair of variables are mutuallycomplementary,which means they cannot be simultaneously measured or known precisely. For example, the position and the linearmomentumin the$x$-direction of a particle are represented by the operators$x$and$-i\hbar {\frac {\partial }{\partial x}}$,respectively (where$\hbar$is thereduced Planck constant). This is the same example except for the constant$-i\hbar$,so again the operators do not commute and the physical meaning is that the position and linear momentum in a given direction are complementary.

See also

• Anticommutative property
• Centralizer and normalizer(also called a commutant)
• Commutative diagram
• Commutative (neurophysiology)
• Commutator
• Parallelogram law
• Particle statistics(for commutativity inphysics)
• Proof that Peano's axioms imply the commutativity of the addition of natural numbers
• Quasi-commutative property
• Trace monoid
• Commuting probability

References

Books

• Axler, Sheldon (1997).Linear Algebra Done Right, 2e.Springer.ISBN0-387-98258-2.

  Abstract algebra theory. Covers commutativity in that context. Uses property throughout book.

• Copi, Irving M.; Cohen, Carl (2005).Introduction to Logic(12th ed.). Prentice Hall.ISBN9780131898349.
• Gallian, Joseph (2006).Contemporary Abstract Algebra(6e ed.). Houghton Mifflin.ISBN0-618-51471-6.

  Linear algebra theory. Explains commutativity in chapter 1, uses it throughout.

• Goodman, Frederick (2003).Algebra: Abstract and Concrete, Stressing Symmetry(2e ed.). Prentice Hall.ISBN0-13-067342-0.

  Abstract algebra theory. Uses commutativity property throughout book.

• Hurley, Patrick J.; Watson, Lori (2016).A Concise Introduction to Logic(12th ed.). Cengage Learning.ISBN978-1-337-51478-1.

Articles

• Lumpkin, B. (1997)."The Mathematical Legacy of Ancient Egypt – A Response To Robert Palter"(PDF)(Unpublished manuscript). Archived fromthe original(PDF)on 13 July 2007.

  Article describing the mathematical ability of ancient civilizations.

• Gay, Robins R.; Shute, Charles C. D. (1987).The Rhind Mathematical Papyrus: An Ancient Egyptian Text.British Museum.ISBN0-7141-0944-4.

  Translation and interpretation of theRhind Mathematical Papyrus.

Online resources

• "Commutativity",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Krowne, Aaron,CommutativeatPlanetMath., Accessed 8 August 2007.

  Definition of commutativity and examples of commutative operations

• Weisstein, Eric W."Commute".MathWorld.,Accessed 8 August 2007.

  Explanation of the term commute

• "Yark".Examples of non-commutative operationsatPlanetMath., Accessed 8 August 2007

  Examples proving some noncommutative operations

• O'Conner, J.J.; Robertson, E.F."History of real numbers".MacTutor.Retrieved8 August2007.

  Article giving the history of the real numbers

• Cabillón, Julio; Miller, Jeff."Earliest Known Uses of Mathematical Terms".Retrieved22 November2008.

  Page covering the earliest uses of mathematical terms

• O'Conner, J.J.; Robertson, E.F."biography of François Servois".MacTutor.Archived fromthe originalon 2 September 2009.Retrieved8 August2007.

  Biography of Francois Servois, who first used the term