Stress (mechanics)

Stress
Stress
	Residual stressesinside a plastic protractor are revealed bypolarized light.
Common symbols	σ
SI unit	pascal
Other units	psi,bar
InSI base units	Pa =kg⋅m−1⋅s−2
Dimension

Incontinuum mechanics,stressis aphysical quantitythat describesforcespresent duringdeformation.For example, an object being pulled apart, such as a stretched elastic band, is subject totensilestress and may undergoelongation.An object being pushed together, such as a crumpled sponge, is subject tocompressivestress and may undergo shortening.^[1]^[2]The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress hasdimensionof force per area, withSI unitsof newtons per square meter (N/m²) orpascal(Pa).^[1]

Stress expresses the internal forces that neighbouringparticlesof a continuous material exert on each other, whilestrainis the measure of the relativedeformationof the material.^[3]For example, when asolidvertical bar is supporting an overheadweight,each particle in the bar pushes on the particles immediately below it. When aliquidis in a closed container underpressure,each particle gets pushed against by all the surrounding particles. The container walls and thepressure-inducing surface (such as a piston) push against them in (Newtonian)reaction.These macroscopic forces are actually the net result of a very large number ofintermolecular forcesandcollisionsbetween the particles in thosemolecules.Stress is frequently represented by a lowercase Greek letter sigma (σ).^[3]

Strain inside a material may arise by various mechanisms, such asstressas applied by external forces to the bulk material (likegravity) or to its surface (likecontact forces,external pressure, orfriction). Anystrain (deformation)of a solid material generates an internalelastic stress,analogous to the reaction force of aspring,that tends to restore the material to its original non-deformed state. In liquids andgases,only deformations that change the volume generate persistent elastic stress. If the deformation changes gradually with time, even in fluids there will usually be someviscous stress,opposing that change. Elastic and viscous stresses are usually combined under the namemechanical stress.

Significant stress may exist even when deformation is negligible or non-existent (a common assumption when modeling the flow of water). Stress may exist in the absence of external forces; suchbuilt-in stressis important, for example, inprestressed concreteandtempered glass.Stress may also be imposed on a material without the application ofnet forces,for example bychanges in temperatureorchemicalcomposition, or by externalelectromagnetic fields(as inpiezoelectricandmagnetostrictivematerials).

The relation between mechanical stress, strain, and thestrain ratecan be quite complicated, although alinear approximationmay be adequate in practice if the quantities are sufficiently small. Stress that exceeds certainstrength limitsof the material will result in permanent deformation (such asplastic flow,fracture,cavitation) or even change itscrystal structureandchemical composition.

History

Roman-era bridge inSwitzerland.The stone arches in the bridge are subject tocompressivestresses.

Incabridge on theApurimac River.The rope in the bridge is subject totensilestresses.

Humans have known about stress inside materials since ancient times. Until the 17th century, this understanding was largely intuitive and empirical, though this did not prevent the development of relatively advanced technologies like thecomposite bowandglass blowing.^[4]

Over several millennia, architects and builders in particular, learned how to put together carefully shaped wood beams and stone blocks to withstand, transmit, and distribute stress in the most effective manner, with ingenious devices such as thecapitals,arches,cupolas,trussesand theflying buttressesofGothic cathedrals.

Ancient and medieval architects did develop some geometrical methods and simple formulas to compute the proper sizes of pillars and beams, but the scientific understanding of stress became possible only after the necessary tools were invented in the 17th and 18th centuries:Galileo Galilei's rigorousexperimental method,René Descartes'scoordinatesandanalytic geometry,andNewton'slaws of motion and equilibriumandcalculus of infinitesimals.^[5]With those tools,Augustin-Louis Cauchywas able to give the first rigorous and general mathematical model of a deformed elastic body by introducing the notions of stress and strain.^[6]Cauchy observed that the force across an imaginary surface was a linear function of its normal vector; and, moreover, that it must be a symmetric function (with zero total momentum). The understanding of stress in liquids started with Newton, who provided a differential formula for friction forces (shear stress) in parallellaminar flow.

Definition

Stress is defined as the force across a small boundary per unit area of that boundary, for all orientations of the boundary.^[7]Derived from a fundamental physical quantity (force) and a purely geometrical quantity (area), stress is also a fundamental quantity, like velocity,torqueorenergy,that can be quantified and analyzed without explicit consideration of the nature of the material or of its physical causes.

Following the basic premises of continuum mechanics, stress is amacroscopicconcept. Namely, the particles considered in its definition and analysis should be just small enough to be treated as homogeneous in composition and state, but still large enough to ignorequantumeffects and the detailed motions of molecules. Thus, the force between two particles is actually the average of a very large number of atomic forces between their molecules; and physical quantities like mass, velocity, and forces that act through the bulk of three-dimensional bodies, like gravity, are assumed to be smoothly distributed over them.^[8]^: 90–106Depending on the context, one may also assume that the particles are large enough to allow the averaging out of other microscopic features, like the grains of ametalrod or thefibersof a piece ofwood.

Quantitatively, the stress is expressed by theCauchy traction vectorTdefined as thetraction forceFbetween adjacent parts of the material across an imaginary separating surfaceS,divided by the area ofS.^[9]^: 41–50In afluidat rest the force is perpendicular to the surface, and is the familiarpressure.In asolid,or in aflowof viscousliquid,the forceFmay not be perpendicular toS;hence the stress across a surface must be regarded a vector quantity, not a scalar. Moreover, the direction and magnitude generally depend on the orientation ofS.Thus the stress state of the material must be described by atensor,called the(Cauchy) stress tensor;which is alinear functionthat relates thenormal vectornof a surfaceSto the traction vectorTacrossS.With respect to any chosencoordinate system,the Cauchy stress tensor can be represented as asymmetric matrixof 3×3 real numbers. Even within ahomogeneousbody, the stress tensor may vary from place to place, and may change over time; therefore, the stress within a material is, in general, a time-varyingtensor field.

Normal and shear

In general, the stressTthat a particlePapplies on another particleQacross a surfaceScan have any direction relative toS.The vectorTmay be regarded as the sum of two components: thenormalstress(compressionortension) perpendicular to the surface, and theshear stressthat is parallel to the surface.

If the normal unit vectornof the surface (pointing fromQtowardsP) is assumed fixed, the normal component can be expressed by a single number, thedot productT·n.This number will be positive ifPis "pulling" onQ(tensile stress), and negative ifPis "pushing" againstQ(compressive stress) The shear component is then the vectorT− (T·n)n.

Units

The dimension of stress is that ofpressure,and therefore its coordinates are measured in the same units as pressure: namely,pascals(Pa, that is,newtonspersquare metre) in theInternational System,orpoundspersquare inch(psi) in theImperial system.Because mechanical stresses easily exceed a million Pascals, MPa, which stands for megapascal, is a common unit of stress.

Causes and effects

Glass vase with thecraqueléeffect. The cracks are the result of brief but intense stress created when the semi-molten piece is briefly dipped in water.^[10]

Stress in a material body may be due to multiple physical causes, including external influences and internal physical processes. Some of these agents (like gravity, changes intemperatureandphase,and electromagnetic fields) act on the bulk of the material, varying continuously with position and time. Other agents (like external loads and friction, ambient pressure, and contact forces) may create stresses and forces that are concentrated on certain surfaces, lines or points; and possibly also on very short time intervals (as in theimpulsesdue to collisions). Inactive matter,self-propulsion of microscopic particles generates macroscopic stress profiles.^[11]In general, the stress distribution in a body is expressed as apiecewise continuous functionof space and time.

Conversely, stress is usually correlated with various effects on the material, possibly including changes in physical properties likebirefringence,polarization,andpermeability.The imposition of stress by an external agent usually creates somestrain (deformation)in the material, even if it is too small to be detected. In a solid material, such strain will in turn generate an internal elastic stress, analogous to the reaction force of a stretchedspring,tending to restore the material to its original undeformed state. Fluid materials (liquids,gasesandplasmas) by definition can only oppose deformations that would change their volume. If the deformation changes with time, even in fluids there will usually be some viscous stress, opposing that change. Such stresses can be either shear or normal in nature. Molecular origin of shear stresses in fluids is given in the article onviscosity.The same for normal viscous stresses can be found in Sharma (2019).^[12]

The relation between stress and its effects and causes, including deformation and rate of change of deformation, can be quite complicated (although alinear approximationmay be adequate in practice if the quantities are small enough). Stress that exceeds certainstrength limitsof the material will result in permanent deformation (such asplastic flow,fracture,cavitation) or even change itscrystal structureandchemical composition.

Simple types

In some situations, the stress within a body may adequately be described by a single number, or by a single vector (a number and a direction). Three suchsimple stresssituations, that are often encountered in engineering design, are theuniaxial normal stress,thesimple shear stress,and theisotropic normal stress.^[13]

Uniaxial normal

A common situation with a simple stress pattern is when a straight rod, with uniform material and cross section, is subjected totensionby opposite forces of magnitude $F$ along its axis. If the system is inequilibriumand not changing with time, and the weight of the bar can be neglected, then through each transversal section of the bar the top part must pull on the bottom part with the same force,Fwith continuity through the full cross-sectional area,A.Therefore, the stress σ throughout the bar, across any horizontal surface, can be expressed simply by the single number σ, calculated simply with the magnitude of those forces,F,and cross sectional area,A. $\sigma ={\frac {F}{A}}$ On the other hand, if one imagines the bar being cut along its length, parallel to the axis, there will be no force (hence no stress) between the two halves across the cut. This type of stress may be called (simple) normal stress or uniaxial stress; specifically, (uniaxial, simple, etc.) tensile stress.^[13]If the load iscompressionon the bar, rather than stretching it, the analysis is the same except that the forceFand the stress $\sigma$ change sign, and the stress is called compressive stress.

This analysis assumes the stress is evenly distributed over the entire cross-section. In practice, depending on how the bar is attached at the ends and how it was manufactured, this assumption may not be valid. In that case, the value $\sigma$ =F/Awill be only the average stress, calledengineering stressornominal stress.If the bar's lengthLis many times its diameterD,and it has no gross defects orbuilt-in stress,then the stress can be assumed to be uniformly distributed over any cross-section that is more than a few timesDfrom both ends. (This observation is known as theSaint-Venant's principle).

Normal stress occurs in many other situations besides axial tension and compression. If an elastic bar with uniform and symmetric cross-section is bent in one of its planes of symmetry, the resultingbending stresswill still be normal (perpendicular to the cross-section), but will vary over the cross section: the outer part will be under tensile stress, while the inner part will be compressed. Another variant of normal stress is thehoop stressthat occurs on the walls of a cylindricalpipeorvesselfilled with pressurized fluid.

Shear

Another simple type of stress occurs when a uniformly thick layer of elastic material like glue or rubber is firmly attached to two stiff bodies that are pulled in opposite directions by forces parallel to the layer; or a section of a soft metal bar that is being cut by the jaws of ascissors-like tool.LetFbe the magnitude of those forces, andMbe the midplane of that layer. Just as in the normal stress case, the part of the layer on one side ofMmust pull the other part with the same forceF.Assuming that the direction of the forces is known, the stress acrossMcan be expressed simply by the single number $\tau$ ,calculated simply with the magnitude of those forces,Fand the cross sectional area,A. $\tau ={\frac {F}{A}}$ Unlike normal stress, thissimple shear stressis directed parallel to the cross-section considered, rather than perpendicular to it.^[13]For any planeSthat is perpendicular to the layer, the net internal force acrossS,and hence the stress, will be zero.

As in the case of an axially loaded bar, in practice the shear stress may not be uniformly distributed over the layer; so, as before, the ratioF/Awill only be an average ( "nominal", "engineering" ) stress. That average is often sufficient for practical purposes.^[14]^: 292Shear stress is observed also when a cylindrical bar such as ashaftis subjected to opposite torques at its ends. In that case, the shear stress on each cross-section is parallel to the cross-section, but oriented tangentially relative to the axis, and increases with distance from the axis. Significant shear stress occurs in the middle plate (the "web" ) ofI-beamsunder bending loads, due to the web constraining the end plates ( "flanges" ).

Isotropic

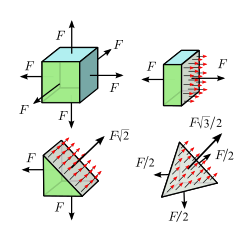
Another simple type of stress occurs when the material body is under equal compression or tension in all directions. This is the case, for example, in a portion of liquid or gas at rest, whether enclosed in some container or as part of a larger mass of fluid; or inside a cube of elastic material that is being pressed or pulled on all six faces by equal perpendicular forces — provided, in both cases, that the material is homogeneous, without built-in stress, and that the effect of gravity and other external forces can be neglected.

In these situations, the stress across any imaginary internal surface turns out to be equal in magnitude and always directed perpendicularly to the surface independently of the surface's orientation. This type of stress may be calledisotropic normalor justisotropic;if it is compressive, it is calledhydrostatic pressureor justpressure.Gases by definition cannot withstand tensile stresses, but some liquids may withstand very large amounts of isotropic tensile stress under some circumstances. seeZ-tube.

Cylinder

Parts withrotational symmetry,such as wheels, axles, pipes, and pillars, are very common in engineering. Often the stress patterns that occur in such parts have rotational or evencylindrical symmetry.The analysis of suchcylinder stressescan take advantage of the symmetry to reduce the dimension of the domain and/or of the stress tensor.

General types

Often, mechanical bodies experience more than one type of stress at the same time; this is calledcombined stress.In normal and shear stress, the magnitude of the stress is maximum for surfaces that are perpendicular to a certain direction $d$ ,and zero across any surfaces that are parallel to $d$ .When the shear stress is zero only across surfaces that are perpendicular to one particular direction, the stress is calledbiaxial,and can be viewed as the sum of two normal or shear stresses. In the most general case, calledtriaxial stress,the stress is nonzero across every surface element.

Cauchy tensor

Combined stresses cannot be described by a single vector. Even if the material is stressed in the same way throughout the volume of the body, the stress across any imaginary surface will depend on the orientation of that surface, in a non-trivial way.

Cauchy observed that the stress vector $T$ across a surface will always be alinear functionof the surface'snormal vector $n$ ,the unit-length vector that is perpendicular to it. That is, $T={\boldsymbol {\sigma }}(n)$ ,where the function ${\boldsymbol {\sigma }}$ satisfies ${\boldsymbol {\sigma }}(\alpha u+\beta v)=\alpha {\boldsymbol {\sigma }}(u)+\beta {\boldsymbol {\sigma }}(v)$ for any vectors $u,v$ and any real numbers $\alpha,\beta$ . The function ${\boldsymbol {\sigma }}$ ,now called the(Cauchy) stress tensor,completely describes the stress state of a uniformly stressed body. (Today, any linear connection between two physical vector quantities is called atensor,reflecting Cauchy's original use to describe the "tensions" (stresses) in a material.) Intensor calculus, ${\boldsymbol {\sigma }}$ is classified as a second-order tensor oftype(0,2) or (1,1) depending on convention.

Like any linear map between vectors, the stress tensor can be represented in any chosenCartesian coordinate systemby a 3×3 matrix of real numbers. Depending on whether the coordinates are numbered $x_{1},x_{2},x_{3}$ or named $x,y,z$ ,the matrix may be written as ${\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}$ or ${\begin{bmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{bmatrix}}$ The stress vector $T={\boldsymbol {\sigma }}(n)$ across a surface withnormal vector $n$ (which iscovariant-"row; horizontal"- vector) with coordinates $n_{1},n_{2},n_{3}$ is then a matrix product $T=n\cdot {\boldsymbol {\sigma }}$ (where T in upper index istransposition,and as a result we getcovariant(row) vector) (look onCauchy stress tensor), that is ${\begin{bmatrix}T_{1}&T_{2}&T_{3}\end{bmatrix}}={\begin{bmatrix}n_{1}&n_{2}&n_{3}\end{bmatrix}}\cdot {\begin{bmatrix}\sigma _{11}&\sigma _{21}&\sigma _{31}\\\sigma _{12}&\sigma _{22}&\sigma _{32}\\\sigma _{13}&\sigma _{23}&\sigma _{33}\end{bmatrix}}$

The linear relation between $T$ and $n$ follows from the fundamental laws ofconservation of linear momentumandstatic equilibriumof forces, and is therefore mathematically exact, for any material and any stress situation. The components of the Cauchy stress tensor at every point in a material satisfy the equilibrium equations (Cauchy's equations of motionfor zero acceleration). Moreover, the principle ofconservation of angular momentumimplies that the stress tensor issymmetric,that is $\sigma _{12}=\sigma _{21}$ , $\sigma _{13}=\sigma _{31}$ ,and $\sigma _{23}=\sigma _{32}$ .Therefore, the stress state of the medium at any point and instant can be specified by only six independent parameters, rather than nine. These may be written ${\begin{bmatrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{xy}&\sigma _{y}&\tau _{yz}\\\tau _{xz}&\tau _{yz}&\sigma _{z}\end{bmatrix}}$ where the elements $\sigma _{x},\sigma _{y},\sigma _{z}$ are called theorthogonal normal stresses(relative to the chosen coordinate system), and $\tau _{xy},\tau _{xz},\tau _{yz}$ theorthogonal shear stresses.^{[citation needed]}

Change of coordinates

The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is theMohr's circleof stress distribution.

As a symmetric 3×3 real matrix, the stress tensor ${\boldsymbol {\sigma }}$ has three mutually orthogonal unit-lengtheigenvectors $e_{1},e_{2},e_{3}$ and three realeigenvalues $\lambda _{1},\lambda _{2},\lambda _{3}$ ,such that ${\boldsymbol {\sigma }}e_{i}=\lambda _{i}e_{i}$ .Therefore, in a coordinate system with axes $e_{1},e_{2},e_{3}$ ,the stress tensor is a diagonal matrix, and has only the three normal components $\lambda _{1},\lambda _{2},\lambda _{3}$ theprincipal stresses.If the three eigenvalues are equal, the stress is anisotropiccompression or tension, always perpendicular to any surface, there is no shear stress, and the tensor is a diagonal matrix in any coordinate frame.

Tensor field

In general, stress is not uniformly distributed over a material body, and may vary with time. Therefore, the stress tensor must be defined for each point and each moment, by considering aninfinitesimalparticle of the medium surrounding that point, and taking the average stresses in that particle as being the stresses at the point.

Thin plates

Human-made objects are often made from stock plates of various materials by operations that do not change their essentially two-dimensional character, like cutting, drilling, gentle bending and welding along the edges. The description of stress in such bodies can be simplified by modeling those parts as two-dimensional surfaces rather than three-dimensional bodies.

In that view, one redefines a "particle" as being an infinitesimal patch of the plate's surface, so that the boundary between adjacent particles becomes an infinitesimal line element; both are implicitly extended in the third dimension, normal to (straight through) the plate. "Stress" is then redefined as being a measure of the internal forces between two adjacent "particles" across their common line element, divided by the length of that line. Some components of the stress tensor can be ignored, but since particles are not infinitesimal in the third dimension one can no longer ignore the torque that a particle applies on its neighbors. That torque is modeled as abending stressthat tends to change thecurvatureof the plate. These simplifications may not hold at welds, at sharp bends and creases (where theradius of curvatureis comparable to the thickness of the plate).

Thin beams

The analysis of stress can be considerably simplified also for thin bars, beams or wires of uniform (or smoothly varying) composition and cross-section that are subjected to moderate bending and twisting. For those bodies, one may consider only cross-sections that are perpendicular to the bar's axis, and redefine a "particle" as being a piece of wire with infinitesimal length between two such cross sections. The ordinary stress is then reduced to a scalar (tension or compression of the bar), but one must take into account also abending stress(that tries to change the bar's curvature, in some direction perpendicular to the axis) and atorsional stress(that tries to twist or un-twist it about its axis).

Analysis

Stress analysisis a branch ofapplied physicsthat covers the determination of the internal distribution of internal forces in solid objects. It is an essential tool in engineering for the study and design of structures such as tunnels, dams, mechanical parts, and structural frames, under prescribed or expected loads. It is also important in many other disciplines; for example, in geology, to study phenomena likeplate tectonics,vulcanism andavalanches;and in biology, to understand the anatomy of living beings.

Goals and assumptions

Stress analysis is generally concerned with objects and structures that can be assumed to be in macroscopicstatic equilibrium.ByNewton's laws of motion,any external forces being applied to such a system must be balanced by internal reaction forces,^[15]^: 97which are almost always surface contact forces between adjacent particles — that is, as stress.^[9]Since every particle needs to be in equilibrium, this reaction stress will generally propagate from particle to particle, creating a stress distribution throughout the body. The typical problem in stress analysis is to determine these internal stresses, given the external forces that are acting on the system. The latter may bebody forces(such as gravity or magnetic attraction), that act throughout the volume of a material;^[16]^: 42–81or concentrated loads (such as friction between an axle and abearing,or the weight of a train wheel on a rail), that are imagined to act over a two-dimensional area, or along a line, or at single point.

In stress analysis one normally disregards the physical causes of the forces or the precise nature of the materials. Instead, one assumes that the stresses are related to deformation (and, in non-static problems, to the rate of deformation) of the material by knownconstitutive equations.^[17]

Methods

Stress analysis may be carried out experimentally, by applying loads to the actual artifact or to scale model, and measuring the resulting stresses, by any of several available methods. This approach is often used for safety certification and monitoring. Most stress is analysed by mathematical methods, especially during design. The basic stress analysis problem can be formulated byEuler's equations of motionfor continuous bodies (which are consequences ofNewton's lawsfor conservation oflinear momentumandangular momentum) and theEuler-Cauchy stress principle,together with the appropriate constitutive equations. Thus one obtains a system ofpartial differential equationsinvolving the stress tensor field and thestrain tensorfield, as unknown functions to be determined. The external body forces appear as the independent ( "right-hand side" ) term in the differential equations, while the concentrated forces appear as boundary conditions. The basic stress analysis problem is therefore aboundary-value problem.

Stress analysis forelasticstructures is based on thetheory of elasticityandinfinitesimal strain theory.When the applied loads cause permanent deformation, one must use more complicated constitutive equations, that can account for the physical processes involved (plastic flow,fracture,phase change,etc.). Engineered structures are usually designed so the maximum expected stresses are well within the range oflinear elasticity(the generalization ofHooke's lawfor continuous media); that is, the deformations caused by internal stresses are linearly related to them. In this case the differential equations that define the stress tensor are linear, and the problem becomes much easier. For one thing, the stress at any point will be a linear function of the loads, too. For small enough stresses, even non-linear systems can usually be assumed to be linear.

Stress analysis is simplified when the physical dimensions and the distribution of loads allow the structure to be treated as one- or two-dimensional. In the analysis of trusses, for example, the stress field may be assumed to be uniform and uniaxial over each member. Then the differential equations reduce to a finite set of equations (usually linear) with finitely many unknowns. In other contexts one may be able to reduce the three-dimensional problem to a two-dimensional one, and/or replace the general stress and strain tensors by simpler models like uniaxial tension/compression, simple shear, etc.

Still, for two- or three-dimensional cases one must solve a partial differential equation problem. Analytical or closed-form solutions to the differential equations can be obtained when the geometry, constitutive relations, and boundary conditions are simple enough. Otherwise one must generally resort to numerical approximations such as thefinite element method,thefinite difference method,and theboundary element method.

Measures

Other useful stress measures include the first and secondPiola–Kirchhoff stress tensors,theBiot stress tensor,and theKirchhoff stress tensor.

References

^^a ^b"12.3 Stress, Strain, and Elastic Modulus - University Physics Volume 1 | OpenStax".openstax.org.19 September 2016.Retrieved2022-11-02.
^"Class Physical-Quantity in theory Physical-Quantities".www-ksl.stanford.edu.Retrieved2022-11-02.
^^a ^b"What is Shear Stress - Materials - Definition".Material Properties.2020-07-31.Retrieved2022-11-02.
^Gordon, J.E. (2003).Structures, or, Why things don't fall down(2. Da Capo Press ed.). Cambridge, MA: Da Capo Press.ISBN 0306812835.
^Jacob Lubliner (2008)."Plasticity Theory"Archived2010-03-31 at theWayback Machine(revised edition). Dover Publications.ISBN 0-486-46290-0
^https://archive.org/details/historyofstrengt0000timo_k8r2/page/110/mode/2up,pp.107-110
^Wai-Fah Chen and Da-Jian Han (2007),"Plasticity for Structural Engineers".J. Ross PublishingISBN 1-932159-75-4
^Peter Chadwick (1999),"Continuum Mechanics: Concise Theory and Problems".Dover Publications, series "Books on Physics".ISBN 0-486-40180-4.pages
^^a ^bI-Shih Liu (2002),"Continuum Mechanics".SpringerISBN 3-540-43019-9
^(2009)The art of making glass.Lamberts Glashütte (LambertsGlas) product brochure. Accessed on 2013-02-08.
^Marchetti, M. C.; Joanny, J. F.; Ramaswamy, S.; Liverpool, T. B.; Prost, J.; Rao, Madan; Simha, R. Aditi (2013). "Hydrodynamics of soft active matter".Reviews of Modern Physics.85(3): 1143–1189.Bibcode:2013RvMP...85.1143M.doi:10.1103/RevModPhys.85.1143.
^Sharma, B and Kumar, R "Estimation of bulk viscosity of dilute gases using a nonequilibrium molecular dynamics approach.",Physical Review E,100, 013309 (2019)
^^a ^b ^cRonald L. Huston and Harold Josephs (2009), "Practical Stress Analysis in Engineering Design". 3rd edition, CRC Press, 634 pages.ISBN 9781574447132
^Walter D. Pilkey, Orrin H. Pilkey (1974),"Mechanics of solids"(book)
^Donald Ray Smith and Clifford Truesdell (1993)"An Introduction to Continuum Mechanics after Truesdell and Noll". Springer.ISBN 0-7923-2454-4
^Fridtjov Irgens (2008),"Continuum Mechanics".Springer.ISBN 3-540-74297-2
^William S. Slaughter (2012),"The Linearized Theory of Elasticity".Birkhäuser BaselISBN 978-0-8176-4117-7