Contact mechanics

Stresses in a contact area loaded simultaneously with a normal and a tangential force. Stresses were made visible usingphotoelasticity.

Contact mechanicsis the study of thedeformationofsolidsthat touch each other at one or more points.A central distinction in contact mechanics is betweenstressesactingperpendicularto the contacting bodies' surfaces (known asnormal stress) andfrictionalstresses actingtangentiallybetween the surfaces (shear stress).Normal contact mechanicsorfrictionless contact mechanicsfocuses on normal stresses caused by appliednormal forcesand by theadhesionpresent on surfaces in close contact, even if they are clean and dry. Frictional contact mechanicsemphasizes the effect of friction forces.

Contact mechanics is part of mechanicalengineering.The physical and mathematical formulation of the subject is built upon themechanics of materialsandcontinuum mechanicsand focuses on computations involvingelastic,viscoelastic,andplasticbodies instaticordynamiccontact. Contact mechanics provides necessary information for the safe and energy efficient design of technical systems and for the study oftribology,contact stiffness,electrical contact resistanceandindentation hardness.Principles of contacts mechanics are implemented towards applications such as locomotive wheel-rail contact,couplingdevices,brakingsystems,tires,bearings,combustion engines,mechanical linkages,gasketseals,metalworking,metal forming,ultrasonic welding,electrical contacts,and many others. Current challenges faced in the field may includestress analysisof contact and coupling members and the influence oflubricationand materialdesignonfrictionandwear.Applications of contact mechanics further extend into themicro- andnanotechnologicalrealm.

The original work in contact mechanics dates back to 1881 with the publication of the paper "On the contact of elastic solids"("Ueber die Berührung fester elastischer Körper") byHeinrich Hertz.Hertz was attempting to understand how the optical properties of multiple, stackedlensesmight change with theforceholding them together. Hertzian contact stress refers to the localized stresses that develop as two curved surfaces come in contact and deform slightly under the imposed loads. This amount of deformation is dependent on themodulus of elasticityof the material in contact. It gives the contact stress as a function of the normal contact force, the radii of curvature of both bodies and the modulus of elasticity of both bodies. Hertzian contact stress forms the foundation for the equations for load bearing capabilities andfatiguelife in bearings, gears, and any other bodies where two surfaces are in contact.

History

When a sphere is pressed against an elastic material, the contact area increases.

Classical contact mechanics is most notably associated with Heinrich Hertz.In 1882, Hertz solved the contact problem of two elastic bodies with curved surfaces. This still-relevant classical solution provides a foundation for modern problems in contact mechanics. For example, inmechanical engineeringandtribology,Hertzian contact stressis a description of the stress within mating parts. The Hertzian contact stress usually refers to the stress close to the area of contact between two spheres of different radii.

It was not until nearly one hundred years later thatJohnson,Kendall, and Roberts found a similar solution for the case ofadhesivecontact.This theory was rejected byBoris Derjaguinand co-workerswho proposed a different theory of adhesionin the 1970s. The Derjaguin model came to be known as the DMT (after Derjaguin, Muller and Toporov) model,and the Johnson et al. model came to be known as the JKR (after Johnson, Kendall and Roberts) model for adhesive elastic contact. This rejection proved to be instrumental in the development of the Taborand later Maugisparameters that quantify which contact model (of the JKR and DMT models) represent adhesive contact better for specific materials.

Further advancement in the field of contact mechanics in the mid-twentieth century may be attributed to names such asBowdenandTabor.Bowden and Tabor were the first to emphasize the importance of surface roughness for bodies in contact.Through investigation of the surface roughness, the true contact area between friction partners is found to be less than the apparent contact area. Such understanding also drastically changed the direction of undertakings in tribology. The works of Bowden and Tabor yielded several theories in contact mechanics of rough surfaces.

The contributions of Archard (1957)must also be mentioned in discussion of pioneering works in this field. Archard concluded that, even for rough elastic surfaces, the contact area is approximately proportional to thenormal force.Further important insights along these lines were provided by Greenwood and Williamson (1966),Bush (1975),and Persson (2002).The main findings of these works were that the true contact surface in rough materials is generally proportional to the normal force, while the parameters of individual micro-contacts (i.e., pressure, size of the micro-contact) are only weakly dependent upon the load.

Classical solutions for non-adhesive elastic contact

The theory of contact between elastic bodies can be used to find contact areas and indentation depths for simple geometries. Some commonly used solutions are listed below. The theory used to compute these solutions is discussed later in the article. Solutions for multitude of other technically relevant shapes, e.g. the truncated cone, the worn sphere, rough profiles, hollow cylinders, etc. can be found in

Contact between a sphere and a half-space

Contact of an elastic sphere with an elastic half-space

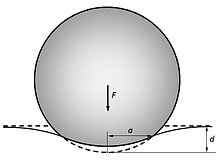
An elasticsphereofradius$R$indents an elastichalf-spacewhere total deformation is$d$,causing a contact area of radius

$a={\sqrt {Rd}}$

The applied force$F$is related to the displacement$d$by

$F={\frac {4}{3}}E^{*}R^{\frac {1}{2}}d^{\frac {3}{2}}$

where

${\frac {1}{E^{*}}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}$

and$E_{1}$,$E_{2}$are theelastic moduliand$\nu _{1}$,$\nu _{2}$thePoisson's ratiosassociated with each body.

The distribution of normal pressure in the contact area as a function of distance from the center of the circle is

$p(r)=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{\frac {1}{2}}$

where$p_{0}$is the maximum contact pressure given by

$p_{0}={\frac {3F}{2\pi a^{2}}}={\frac {1}{\pi }}\left({\frac {6F{E^{*}}^{2}}{R^{2}}}\right)^{\frac {1}{3}}$

The radius of the circle is related to the applied load$F$by the equation

$a^{3}={\cfrac {3FR}{4E^{*}}}$

The total deformation$d$is related to the maximum contact pressure by

$d={\frac {a^{2}}{R}}=\left({\frac {9F^{2}}{16{E^{*}}^{2}R}}\right)^{\frac {1}{3}}$

The maximum shear stress occurs in the interior at$z\approx 0.49a$for$\nu =0.33$.

Contact between two spheres

Contact between two spheres.

Contact between two crossed cylinders of equal radius.

For contact between two spheres of radii$R_{1}$and$R_{2}$,the area of contact is a circle of radius$a$.The equations are the same as for a sphere in contact with a half plane except that the effective radius$R$is defined as

${\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}$

Contact between two crossed cylinders of equal radius

This is equivalent to contact between a sphere of radius$R$and aplane.

Contact between a rigid cylinder with flat end and an elastic half-space

Contact between a rigid cylindrical indenter and an elastic half-space.

If a rigidcylinderis pressed into an elastic half-space, it creates a pressure distribution described by

$p(r)=p_{0}\left(1-{\frac {r^{2}}{R^{2}}}\right)^{-{\frac {1}{2}}}$

where$R$is the radius of the cylinder and

$p_{0}={\frac {1}{\pi }}E^{*}{\frac {d}{R}}$

The relationship between the indentation depth and the normal force is given by

$F=2RE^{*}d$

Contact between a rigid conical indenter and an elastic half-space

Contact between a rigid conical indenter and an elastic half-space.

In the case ofindentationof an elastic half-space of Young's modulus$E$using a rigidconicalindenter, the depth of the contact region$\epsilon$and contact radius$a$are related by

$\epsilon =a\tan(\theta )$

with$\theta$defined as the angle between the plane and the side surface of the cone. The total indentation depth$d$is given by:

$d={\frac {\pi }{2}}\epsilon$

The total force is

$F={\frac {\pi E}{2\left(1-\nu ^{2}\right)}}a^{2}\tan(\theta )={\frac {2E}{\pi \left(1-\nu ^{2}\right)}}{\frac {d^{2}}{\tan(\theta )}}$

The pressure distribution is given by

$p\left(r\right)={\frac {Ed}{\pi a\left(1-\nu ^{2}\right)}}\ln \left({\frac {a}{r}}+{\sqrt {\left({\frac {a}{r}}\right)^{2}-1}}\right)={\frac {Ed}{\pi a\left(1-\nu ^{2}\right)}}\cosh ^{-1}\left({\frac {a}{r}}\right)$

The stress has alogarithmicsingularityat the tip of the cone.

Contact between two cylinders with parallel axes

Contact between two cylinders with parallel axes

In contact between two cylinders with parallel axes, the force is linearly proportional to the length of cylindersLand to the indentation depthd:

$F\approx {\frac {\pi }{4}}E^{*}Ld$

The radii of curvature are entirely absent from this relationship. The contact radius is described through the usual relationship

$a={\sqrt {Rd}}$

with

${\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}$

as in contact between two spheres. The maximum pressure is equal to

$p_{0}=\left({\frac {E^{*}F}{\pi LR}}\right)^{\frac {1}{2}}$

Bearing contact

Main article:Bearing pressure

The contact in the case ofbearingsis often a contact between a convex surface (male cylinder or sphere) and a concave surface (female cylinder or sphere:boreorhemispherical cup).

The Method of Dimensionality Reduction

Contact between a sphere and an elastic half-space and one-dimensional replaced model.

Some contact problems can be solved with the Method of Dimensionality Reduction (MDR). In this method, the initial three-dimensional system is replaced with a contact of a body with a linear elastic or viscoelastic foundation (see fig.). The properties of one-dimensional systems coincide exactly with those of the original three-dimensional system, if the form of the bodies is modified and the elements of the foundation are defined according to the rules of the MDR.MDR is based on the solution to axisymmetric contact problems first obtained by Ludwig Föppl (1941) and Gerhard Schubert (1942)

However, for exact analytical results, it is required that the contact problem is axisymmetric and the contacts are compact.

Hertzian theory of non-adhesive elastic contact

The classical theory of contact focused primarily on non-adhesive contact where no tension force is allowed to occur within the contact area, i.e., contacting bodies can be separated without adhesion forces. Several analytical and numerical approaches have been used to solve contact problems that satisfy the no-adhesion condition. Complex forces andmomentsare transmitted between the bodies where they touch, so problems in contact mechanics can become quite sophisticated. In addition, the contact stresses are usually a nonlinear function of the deformation. To simplify the solution procedure, aframe of referenceis usually defined in which the objects (possibly in motion relative to one another) are static. They interact through surface tractions (or pressures/stresses) at their interface.

As an example, consider two objects which meet at some surface$S$in the ($x$,$y$)-plane with the$z$-axis assumed normal to the surface. One of the bodies will experience a normally-directedpressuredistribution$p_{z}=p(x,y)=q_{z}(x,y)$and in-planesurface tractiondistributions$q_{x}=q_{x}(x,y)$and$q_{y}=q_{y}(x,y)$over the region$S$.In terms of aNewtonianforce balance, the forces:

$P_{z}=\int _{S}p(x,y)~\mathrm {d} A~;~~Q_{x}=\int _{S}q_{x}(x,y)~\mathrm {d} A~;~~Q_{y}=\int _{S}q_{y}(x,y)~\mathrm {d} A$

must be equal and opposite to the forces established in the other body. The moments corresponding to these forces:

$M_{x}=\int _{S}y~q_{z}(x,y)~\mathrm {d} A~;~~M_{y}=\int _{S}-x~q_{z}(x,y)~\mathrm {d} A~;~~M_{z}=\int _{S}[x~q_{y}(x,y)-y~q_{x}(x,y)]~\mathrm {d} A$

are also required to cancel between bodies so that they arekinematicallyimmobile.

Assumptions in Hertzian theory

The following assumptions are made in determining the solutions ofHertziancontact problems:

• The strains are small and within the elastic limit.
• The surfaces are continuous and non-conforming (implying that the area of contact is much smaller than the characteristic dimensions of the contacting bodies).
• Each body can be considered an elastic half-space.
• The surfaces are frictionless.

Additional complications arise when some or all these assumptions are violated and such contact problems are usually callednon-Hertzian.

Analytical solution techniques

Contact between two spheres.

Analytical solution methods for non-adhesive contact problem can be classified into two types based on the geometry of the area of contact.Aconforming contactis one in which the two bodies touch at multiple points before any deformation takes place (i.e., they just "fit together" ). Anon-conforming contactis one in which the shapes of the bodies are dissimilar enough that, under zero load, they only touch at a point (or possibly along a line). In the non-conforming case, the contact area is small compared to the sizes of the objects and thestressesare highly concentrated in this area. Such a contact is calledconcentrated,otherwise it is calleddiversified.

A common approach inlinear elasticityis tosuperposea number of solutions each of which corresponds to a point load acting over the area of contact. For example, in the case of loading of ahalf-plane,theFlamant solutionis often used as a starting point and then generalized to various shapes of the area of contact. The force and moment balances between the two bodies in contact act as additional constraints to the solution.

Point contact on a (2D) half-plane

Main article:Flamant solution

Schematic of the loading on a plane by force P at a point (0, 0).

A starting point for solving contact problems is to understand the effect of a "point-load" applied to an isotropic, homogeneous, and linear elastic half-plane, shown in the figure to the right. The problem may be eitherplane stressorplane strain.This is aboundary value problemof linear elasticity subject to the tractionboundary conditions:

$\sigma _{xz}(x,0)=0~;~~\sigma _{z}(x,z)=-P\delta (x,z)$

where$\delta (x,z)$is theDirac delta function.The boundary conditions state that there are no shear stresses on the surface and a singular normal force P is applied at (0, 0). Applying these conditions to the governing equations of elasticity produces the result

${\begin{aligned}\sigma _{xx}&=-{\frac {2P}{\pi }}{\frac {x^{2}z}{\left(x^{2}+z^{2}\right)^{2}}}\\\sigma _{zz}&=-{\frac {2P}{\pi }}{\frac {z^{3}}{\left(x^{2}+z^{2}\right)^{2}}}\\\sigma _{xz}&=-{\frac {2P}{\pi }}{\frac {xz^{2}}{\left(x^{2}+z^{2}\right)^{2}}}\end{aligned}}$

for some point,$(x,y)$,in the half-plane. The circle shown in the figure indicates a surface on which the maximum shear stress is constant. From this stress field, thestraincomponents and thus thedisplacementsof all material points may be determined.

Line contact on a (2D) half-plane

Normal loading over a region

Suppose, rather than a point load$P$,a distributed load$p(x)$is applied to the surface instead, over the range$a<x<b$.The principle of linear superposition can be applied to determine the resulting stress field as the solution to theintegralequations:

${\begin{aligned}\sigma _{xx}&=-{\frac {2z}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\left(x-x'\right)^{2}\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}~;~~\sigma _{zz}=-{\frac {2z^{3}}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\\[3pt]\sigma _{xz}&=-{\frac {2z^{2}}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\left(x-x'\right)\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\end{aligned}}$

Shear loading over a region

The same principle applies for loading on the surface in the plane of the surface. These kinds of tractions would tend to arise as a result of friction. The solution is similar the above (for both singular loads$Q$and distributed loads$q(x)$) but altered slightly:

${\begin{aligned}\sigma _{xx}&=-{\frac {2}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(x-x'\right)^{3}\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}~;~~\sigma _{zz}=-{\frac {2z^{2}}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(x-x'\right)\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\\[3pt]\sigma _{xz}&=-{\frac {2z}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(x-x'\right)^{2}\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\end{aligned}}$

These results may themselves be superposed onto those given above for normal loading to deal with more complex loads.

Point contact on a (3D) half-space

Analogously to the Flamant solution for the 2D half-plane, fundamental solutions are known for the linearly elastic 3D half-space as well. These were found byBoussinesqfor a concentrated normal load and by Cerruti for a tangential load. See the section on this inLinear elasticity.

Numerical solution techniques

Distinctions between conforming and non-conforming contact do not have to be made when numerical solution schemes are employed to solve contact problems. These methods do not rely on further assumptions within the solution process since they base solely on the general formulation of the underlying equations.Besides the standard equations describing the deformation and motion of bodies two additional inequalities can be formulated. The first simply restricts the motion and deformation of the bodies by the assumption that no penetration can occur. Hence the gap$h$between two bodies can only be positive or zero

$h\geq 0$

where$h=0$denotes contact. The second assumption in contact mechanics is related to the fact, that no tension force is allowed to occur within the contact area (contacting bodies can be lifted up without adhesion forces). This leads to an inequality which the stresses have to obey at the contact interface. It is formulated for the normal stress$\sigma _{n}=\mathbf {t} \cdot \mathbf {n}$.

At locations where there is contact between the surfaces the gap is zero, i.e.$h=0$,and there the normal stress is different than zero, indeed,$\sigma _{n}<0$.At locations where the surfaces are not in contact the normal stress is identical to zero;$\sigma _{n}=0$,while the gap is positive; i.e.,$h>0$.This type of complementarity formulation can be expressed in the so-calledKuhn–Tuckerform, viz.

$h\geq 0\,,\quad \sigma _{n}\leq 0\,,\quad \sigma _{n}\,h=0\,.$

These conditions are valid in a general way. The mathematical formulation of the gap depends upon the kinematics of the underlying theory of the solid (e.g., linear or nonlinear solid in two- or three dimensions,beamorshellmodel). By restating the normal stress$\sigma _{n}$in terms of the contact pressure,$p$;i.e.,$p=-\sigma _{n}$the Kuhn-Tucker problem can be restated as in standard complementarity form i.e.$$h\geq 0\,,\quad p\geq 0\,,\quad p\,h=0\,.$$In the linear elastic case the gap can be formulated as$${h}=h_{0}+{g}+u,$$where$h_{0}$is the rigid body separation,$g$is the geometry/topography of the contact (cylinder and roughness) and$u$is the elastic deformation/deflection. If the contacting bodies are approximated as linear elastic half spaces, the Boussinesq-Cerruti integral equation solution can be applied to express the deformation ($u$) as a function of the contact pressure ($p$); i.e.,$$u=\int _{\infty }^{\infty }K(x-s)p(s)ds,$$where$$K(x-s)={\frac {2}{\pi E^{*}}}\ln |x-s|$$for line loading of an elastic half space and$$K(x-s)={\frac {1}{\pi E^{*}}}{\frac {1}{\sqrt {\left(x_{1}-s_{1}\right)^{2}+\left(x_{2}-s_{2}\right)^{2}}}}$$for point loading of an elastic half-space.

After discretization the linear elastic contact mechanics problem can be stated in standard Linear Complementarity Problem (LCP) form.

${\begin{aligned}\mathbf {h} &=\mathbf {h} _{0}+\mathbf {g} +\mathbf {Cp},\\\mathbf {h} \cdot \mathbf {p} &=0,\,\,\,\mathbf {p} \geq 0,\,\,\,\mathbf {h} \geq 0,\\\end{aligned}}$

where$\mathbf {C}$is a matrix, whose elements are so called influence coefficients relating the contact pressure and the deformation. The strict LCP formulation of the CM problem presented above, allows for direct application of well-established numerical solution techniques such asLemke's pivoting algorithm.The Lemke algorithm has the advantage that it finds the numerically exact solution within a finite number of iterations. The MATLAB implementation presented byAlmqvist et al.is one example that can be employed to solve the problem numerically. In addition, an example code for an LCP solution of a 2D linear elastic contact mechanics problem has also been made public at MATLAB file exchange byAlmqvist et al.

Contact between rough surfaces

When two bodies with rough surfaces are pressed against each other, the true contact area formed between the two bodies,$A$,is much smaller than the apparent or nominal contact area$A_{0}$.The mechanics of contacting rough surfaces are discussed in terms of normal contact mechanics and static frictional interactions.Natural and engineering surfaces typically exhibit roughness features, known as asperities, across a broad range of length scales down to the molecular level, with surface structures exhibiting self affinity, also known assurface fractality.It is recognized that the self affine structure of surfaces is the origin of the linear scaling of true contact area with applied pressure.Assuming a model of shearing welded contacts intribologicalinteractions, this ubiquitously observed linearity between contact area and pressure can also be considered the origin of the linearity of the relationship between static friction and applied normal force.

In contact between a "random rough" surface and an elastic half-space, the true contact area is related to the normal force$F$by

$A={\frac {\kappa }{E^{*}h'}}F$

with$h'$equal to the root mean square (also known as the quadratic mean) of the surface slope and$\kappa \approx 2$.The median pressure in the true contact surface

$p_{\mathrm {av} }={\frac {F}{A}}\approx {\frac {1}{2}}E^{*}h'$

can be reasonably estimated as half of the effective elastic modulus$E^{*}$multiplied with the root mean square of the surface slope$h'$.

An overview of the GW model

Greenwood and Williamson in 1966 (GW)proposed a theory of elastic contact mechanics of rough surfaces which is today the foundation of many theories in tribology (friction, adhesion, thermal and electrical conductance, wear, etc.). They considered the contact between a smooth rigid plane and a nominally flat deformable rough surface covered with round tip asperities of the same radius R. Their theory assumes that the deformation of each asperity is independent of that of its neighbours and is described by the Hertz model. The heights of asperities have a random distribution. The probability that asperity height is between$z$and$z+dz$is$\phi (z)dz$.The authors calculated the number of contact spots n, the total contact area$A_{r}$and the total load P in general case. They gave those formulas in two forms: in the basic and using standardized variables. If one assumes that N asperities covers a rough surface, then the expected number of contacts is

$n=N\int _{d}^{\infty }\phi (z)dz$

The expected total area of contact can be calculated from the formula

$A_{a}=N\pi R\int _{d}^{\infty }(z-d)\phi (z)dz$

and the expected total force is given by

$P={\frac {4}{3}}NE_{r}{\sqrt {R}}\int _{d}^{\infty }(z-d)^{\frac {3}{2}}\phi (z)dz$

where:

R, radius of curvature of the microasperity,

z, height of the microasperity measured from the profile line,

d, close the surface,

$E_{r}=\left({\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}\right)^{-1}$,composite Young's modulus of elasticity,

$E_{i}$,modulus of elasticity of the surface,

$\nu _{i}$,Poisson's surface coefficients.

Greenwood and Williamson introduced standardized separation$h=d/\sigma$and standardized height distribution$\phi ^{*}(s)$whose standard deviation is equal to one. Below are presented the formulas in the standardized form.

${\begin{aligned}F_{n}(h)&=\int _{h}^{\infty }(s-h)^{n}\phi ^{*}(s)ds\\n&=\eta A_{n}F_{0}(h)\\A_{a}&=\pi \eta AR\sigma F_{1}(h)\\P&={\frac {4}{3}}\eta AE_{r}{\sqrt {R}}\sigma ^{\frac {3}{2}}F_{\frac {3}{2}}(h)\end{aligned}}$

where:

d is the separation,

$A$is the nominal contact area,

$\eta$is the surface density of asperities,

$E^{*}$is the effective Young modulus.

$A$and$P$can be determined when the$F_{n}(h)$terms are calculated for the given surfaces using the convolution of the surface roughness$\phi ^{*}(s)$.Several studies have followed the suggested curve fits for$F_{n}(h)$assuming a Gaussian surface high distribution with curve fits presented by Arcoumanis et al.and Jedynakamong others. It has been repeatedly observed that engineering surfaces do not demonstrate Gaussian surface height distributions e.g. Peklenik.Leighton et al.presented fits for crosshatched IC engine cylinder liner surfaces together with a process for determining the$F_{n}(h)$terms for any measured surfaces. Leighton et al.demonstrated that Gaussian fit data is not accurate for modelling any engineered surfaces and went on to demonstratethat early running of the surfaces results in a gradual transition which significantly changes the surface topography, load carrying capacity and friction.

Recently the exact approximants to$A_{r}$and$P$were published by Jedynak.They are given by the following rational formulas, which are approximants to the integrals$F_{n}(h)$.They are calculated for the Gaussian distribution of asperities, which have been shown to be unrealistic for engineering surface but can be assumed where friction, load carrying capacity or real contact area results are not critical to the analysis.

$F_{n}(h)={\frac {a_{0}+a_{1}h+a_{2}h^{2}+a_{3}h^{3}}{1+b_{1}h+b_{2}h^{2}+b_{3}h^{3}+b_{4}h^{4}+b_{5}h^{5}+b_{6}h^{6}}}\exp \left(-{\frac {h^{2}}{2}}\right)$

For$F_{1}(h)$the coefficients are

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.398942280401,0.159773702775,0.0389687688311,0.00364356495452]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=\left[1.653807476138,1.170419428529,0.448892964428,0.0951971709160,0.00931642803836,-6.383774657279\times 10^{-6}\right]\end{aligned}}$

The maximum relative error is$9.93\times 10^{-8}\%$.

For$F_{\frac {3}{2}}(h)$the coefficients are

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.430019993662,0.101979509447,0.0229040629580,0.000688602924]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1.671117125984,1.199586555505,0.46936532151,0.102632881122,0.010686348714,0.0000517200271]\end{aligned}}$

The maximum relative error is$1.91\times 10^{-7}\%$.The paperalso contains the exact expressions for$F_{n}(h)$

${\begin{aligned}F_{1}(h)&={\frac {1}{\sqrt {2\pi }}}\exp \left(-{\frac {1}{2}}h^{2}\right)-{\frac {1}{2}}h\,\operatorname {erfc} \left({\frac {h}{\sqrt {2}}}\right)\\F_{\frac {3}{2}}(h)&={\frac {1}{4{\sqrt {\pi }}}}\exp \left(-{\frac {h^{2}}{4}}\right){\sqrt {h}}\left(\left(h^{2}+1\right)K_{\frac {1}{4}}\left({\frac {h^{2}}{4}}\right)-h^{2}K_{\frac {3}{4}}\left({\frac {h^{2}}{4}}\right)\right)\end{aligned}}$

where erfc(z) means the complementary error function and$K_{\nu }(z)$is the modified Bessel function of the second kind.

For the situation where the asperities on the two surfaces have a Gaussian height distribution and the peaks can be assumed to be spherical,the average contact pressure is sufficient to cause yield when$p_{\text{av}}=1.1\sigma _{y}\approx 0.39\sigma _{0}$where$\sigma _{y}$is the uniaxialyield stressand$\sigma _{0}$is the indentation hardness.Greenwood and Williamsondefined a dimensionless parameter$\Psi$called theplasticity indexthat could be used to determine whether contact would be elastic or plastic.

The Greenwood-Williamson model requires knowledge of two statistically dependent quantities; the standard deviation of the surface roughness and the curvature of the asperity peaks. An alternative definition of the plasticity index has been given by Mikic.Yield occurs when the pressure is greater than the uniaxial yield stress. Since the yield stress is proportional to the indentation hardness$\sigma _{0}$,Mikic defined the plasticity index for elastic-plastic contact to be

$\Psi ={\frac {E^{*}h'}{\sigma _{0}}}>{\frac {2}{3}}~.$

In this definition$\Psi$represents the micro-roughness in a state of complete plasticity and only one statistical quantity, the rms slope, is needed which can be calculated from surface measurements. For$\Psi <{\frac {2}{3}}$,the surface behaves elastically during contact.

In both the Greenwood-Williamson and Mikic models the load is assumed to be proportional to the deformed area. Hence, whether the system behaves plastically or elastically is independent of the applied normal force.

An overview of the GT model

The model proposed by Greenwood and Tripp (GT),extended the GW model to contact between two rough surfaces. The GT model is widely used in the field of elastohydrodynamic analysis.

The most frequently cited equations given by the GT model are for the asperity contact area

$A_{a}=\pi ^{2}(\eta \beta \sigma )^{2}AF_{2}(\lambda ),$

and load carried by asperities

$P={\frac {8{\sqrt {2}}}{15}}\pi (\eta \beta \sigma )^{2}{\sqrt {\frac {\sigma }{\beta }}}E'AF_{\frac {5}{2}}(\lambda ),$

where:

$\eta \beta \sigma$,roughness parameter,

$A$,nominal contact area,

$\lambda$,Stribeck oil film parameter, first defined by Stribeck \cite{gt} as$\lambda =h/\sigma$,

$E'$,effective elastic modulus,

$F_{2},F_{\frac {5}{2}}(\lambda )$,statistical functions introduced to match the assumed Gaussian distribution of asperities.

Leighton et al.presented fits for crosshatched IC engine cylinder liner surfaces together with a process for determining the$F_{n}(h)$terms for any measured surfaces. Leighton et al.demonstrated that Gaussian fit data is not accurate for modelling any engineered surfaces and went on to demonstratethat early running of the surfaces results in a gradual transition which significantly changes the surface topography, load carrying capacity and friction.

The exact solutions for$A_{a}$and$P$are firstly presented by Jedynak.They are expressed by$F_{n}$as follows. They are calculated for the Gaussian distribution of asperities, which have been shown to be unrealistic for engineering surface but can be assumed where friction, load carrying capacity or real contact area results are not critical to the analysis.

${\begin{aligned}F_{2}&={\frac {1}{2}}\left(h^{2}+1\right)\operatorname {erfc} \left({\frac {h}{\sqrt {2}}}\right)-{\frac {h}{\sqrt {2\pi }}}\exp \left(-{\frac {h^{2}}{2}}\right)\\F_{\frac {5}{2}}&={\frac {1}{8{\sqrt {\pi }}}}\exp \left(-{\frac {h^{2}}{4}}\right)h^{\frac {3}{2}}\left(\left(2h^{2}+3\right)K_{\frac {3}{4}}\left({\frac {h^{2}}{4}}\right)-\left(2h^{2}+5\right)K_{\frac {1}{4}}\left({\frac {h^{2}}{4}}\right)\right)\end{aligned}}$

where erfc(z) means the complementary error function and$K_{\nu }(z)$is the modified Bessel function of the second kind.

In paperone can find comprehensive review of existing approximants to$F_{\frac {5}{2}}$.New proposals give the most accurate approximants to$F_{\frac {5}{2}}$and$F_{2}$,which are reported in the literature. They are given by the following rational formulas, which are very exact approximants to integrals$F_{n}(h)$.They are calculated for the Gaussian distribution of asperities

$F_{n}(h)={\frac {a_{0}+a_{1}h+a_{2}h^{2}+a_{3}h^{3}}{1+b_{1}h+b_{2}h^{2}+b_{3}h^{3}+b_{4}h^{4}+b_{5}h^{5}+b_{6}h^{6}}}\exp \left(-{\frac {h^{2}}{2}}\right)$

For$F_{2}(h)$the coefficients are

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.5,0.182536384941,0.039812283118,0.003684879001]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1.960841785003,1.708677456715,0.856592986083,0.264996791567,0.049257843893,0.004640740133]\end{aligned}}$

The maximum relative error is$1.68\times 10^{-7}\%$.

For$F_{\frac {5}{2}}(h)$the coefficients are

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.616634218997,0.108855827811,0.023453835635,0.000449332509]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1.919948267476,1.635304362591,0.799392556572,0.240278859212,0.043178653945,0.003863334276]\end{aligned}}$

The maximum relative error is$4.98\times 10^{-8}\%$.

Adhesive contact between elastic bodies

When two solid surfaces are brought into close proximity, they experience attractivevan der Waals forces.Bradley's van der Waals modelprovides a means of calculating the tensile force between two rigid spheres with perfectly smooth surfaces. The Hertzian model of contact does not consider adhesion possible. However, in the late 1960s, several contradictions were observed when the Hertz theory was compared with experiments involving contact between rubber and glass spheres.

It was observedthat, though Hertz theory applied at large loads, at low loads

• the area of contact was larger than that predicted by Hertz theory,
• the area of contact had a non-zero value even when the load was removed, and
• there was even strong adhesion if the contacting surfaces were clean and dry.

This indicated that adhesive forces were at work. The Johnson-Kendall-Roberts (JKR) model and the Derjaguin-Muller-Toporov (DMT) models were the first to incorporate adhesion into Hertzian contact.

Bradley model of rigid contact

It is commonly assumed that the surface force between two atomic planes at a distance$z$from each other can be derived from theLennard-Jones potential.With this assumption

$F(z)={\cfrac {16\gamma }{3z_{0}}}\left[\left({\cfrac {z}{z_{0}}}\right)^{-9}-\left({\cfrac {z}{z_{0}}}\right)^{-3}\right]$

where$F$is the force (positive in compression),$2\gamma$is the total surface energy ofbothsurfaces per unit area, and$z_{0}$is the equilibrium separation of the two atomic planes.

The Bradley model applied the Lennard-Jones potential to find the force of adhesion between two rigid spheres. The total force between the spheres is found to be

$F_{a}(z)={\cfrac {16\gamma \pi R}{3}}\left[{\cfrac {1}{4}}\left({\cfrac {z}{z_{0}}}\right)^{-8}-\left({\cfrac {z}{z_{0}}}\right)^{-2}\right]~;~~{\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}$

where$R_{1},R_{2}$are the radii of the two spheres.

The two spheres separate completely when thepull-off forceis achieved at$z=z_{0}$at which point

$F_{a}=F_{c}=-4\gamma \pi R.$

Johnson-Kendall-Roberts (JKR) model of elastic contact

Schematic of contact area for the JKR model.

JKR test with a rigid bead on a deformable planar material: complete cycle

To incorporate the effect of adhesion in Hertzian contact, Johnson, Kendall, andRobertsformulated the JKR theory of adhesive contact using a balance between the storedelastic energyand the loss insurface energy.The JKR model considers the effect of contact pressure and adhesion only inside the area of contact. The general solution for the pressure distribution in the contact area in the JKR model is

$p(r)=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{\frac {1}{2}}+p_{0}'\left(1-{\frac {r^{2}}{a^{2}}}\right)^{-{\frac {1}{2}}}$

Note that in the original Hertz theory, the term containing$p_{0}'$was neglected on the ground that tension could not be sustained in the contact zone. For contact between two spheres

$p_{0}={\frac {2aE^{*}}{\pi R}};\quad p_{0}'=-\left({\frac {4\gamma E^{*}}{\pi a}}\right)^{\frac {1}{2}}$

where$a\,$is the radius of the area of contact,$F$is the applied force,$2\gamma$is the total surface energy ofbothsurfaces per unit contact area, $R_{i},\,E_{i},\,\nu _{i},~~i=1,2$are the radii, Young's moduli, and Poisson's ratios of the two spheres, and

${\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}};\quad {\frac {1}{E^{*}}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}$

The approach distance between the two spheres is given by

$d={\frac {\pi a}{2E^{*}}}\left(p_{0}+2p_{0}'\right)={\frac {a^{2}}{R}}$

The Hertz equation for the area of contact between two spheres, modified to take into account the surface energy, has the form

$a^{3}={\frac {3R}{4E^{*}}}\left(F+6\gamma \pi R+{\sqrt {12\gamma \pi RF+(6\gamma \pi R)^{2}}}\right)$

When the surface energy is zero,$\gamma =0$,the Hertz equation for contact between two spheres is recovered. When the applied load is zero, the contact radius is

$a^{3}={\frac {9R^{2}\gamma \pi }{E^{*}}}$

The tensile load at which the spheres are separated (i.e.,$a=0$) is predicted to be

$F_{\text{c}}=-3\gamma \pi R\,$

This force is also called thepull-off force.Note that this force is independent of the moduli of the two spheres. However, there is another possible solution for the value of$a$at this load. This is the critical contact area$a_{\text{c}}$,given by

$a_{\text{c}}^{3}={\frac {9R^{2}\gamma \pi }{4E^{*}}}$

If we define thework of adhesionas

$\Delta \gamma =\gamma _{1}+\gamma _{2}-\gamma _{12}$

where$\gamma _{1},\gamma _{2}$are the adhesive energies of the two surfaces and$\gamma _{12}$is an interaction term, we can write the JKR contact radius as

$a^{3}={\frac {3R}{4E^{*}}}\left(F+3\Delta \gamma \pi R+{\sqrt {6\Delta \gamma \pi RF+(3\Delta \gamma \pi R)^{2}}}\right)$

The tensile load at separation is

$F=-{\frac {3}{2}}\Delta \gamma \pi R\,$

and the critical contact radius is given by

$a_{\text{c}}^{3}={\frac {9R^{2}\Delta \gamma \pi }{8E^{*}}}$

The critical depth of penetration is

$d_{\text{c}}={\frac {a_{c}^{2}}{R}}=\left(R^{\frac {1}{2}}{\frac {9\Delta \gamma \pi }{4E^{*}}}\right)^{\frac {2}{3}}$

Derjaguin-Muller-Toporov (DMT) model of elastic contact

The Derjaguin-Muller-Toporov (DMT) modelis an alternative model for adhesive contact which assumes that the contact profile remains the same as in Hertzian contact but with additional attractive interactions outside the area of contact.

The radius of contact between two spheres from DMT theory is

$a^{3}={\cfrac {3R}{4E^{*}}}\left(F+4\gamma \pi R\right)$

and the pull-off force is

$F_{c}=-4\gamma \pi R\,$

When the pull-off force is achieved the contact area becomes zero and there is no singularity in the contact stresses at the edge of the contact area.

In terms of the work of adhesion$\Delta \gamma$

$a^{3}={\cfrac {3R}{4E^{*}}}\left(F+2\Delta \gamma \pi R\right)$

and

$F_{c}=-2\Delta \gamma \pi R\,$

Tabor parameter

In 1977, Taborshowed that the apparent contradiction between the JKR and DMT theories could be resolved by noting that the two theories were the extreme limits of a single theory parametrized by theTabor parameter($\mu$) defined as

$\mu:={\frac {d_{c}}{z_{0}}}\approx \left[{\frac {R(\Delta \gamma )^{2}}{{E^{*}}^{2}z_{0}^{3}}}\right]^{\frac {1}{3}}$

where$z_{0}$is the equilibrium separation between the two surfaces in contact. The JKR theory applies to large, compliant spheres for which$\mu$is large. The DMT theory applies for small, stiff spheres with small values of$\mu$.

Subsequently, Derjaguin and his collaboratorsby applying Bradley's surface force law to an elastic half space, confirmed that as the Tabor parameter increases, the pull-off force falls from the Bradley value$2\pi R\Delta \gamma$to the JKR value$(3/2)\pi R\Delta \gamma$.More detailed calculations were later done by Greenwoodrevealing the S-shaped load/approach curve which explains the jumping-on effect. A more efficient method of doing the calculations and additional results were given by Feng

Maugis-Dugdale model of elastic contact

Schematic of contact area for the Maugis-Dugdale model.

Further improvement to the Tabor idea was provided by Maugiswho represented the surface force in terms of a Dugdalecohesive zoneapproximation such that the work of adhesion is given by

$\Delta \gamma =\sigma _{0}~h_{0}$

where$\sigma _{0}$is the maximum force predicted by the Lennard-Jones potential and$h_{0}$is the maximum separation obtained by matching the areas under the Dugdale and Lennard-Jones curves (see adjacent figure). This means that the attractive force is constant for$z_{0}\leq z\leq z_{0}+h_{0}$.There is not further penetration in compression. Perfect contact occurs in an area of radius$a$and adhesive forces of magnitude$\sigma _{0}$extend to an area of radius$c>a$.In the region$a<r<c$,the two surfaces are separated by a distance$h(r)$with$h(a)=0$and$h(c)=h_{0}$.The ratio$m$is defined as

$m:={\frac {c}{a}}$.

In the Maugis-Dugdale theory,the surface traction distribution is divided into two parts - one due to the Hertz contact pressure and the other from the Dugdale adhesive stress. Hertz contact is assumed in the region$-a<r<a$.The contribution to the surface traction from the Hertz pressure is given by

$p^{H}(r)=\left({\frac {3F^{H}}{2\pi a^{2}}}\right)\left(1-{\frac {r^{2}}{a^{2}}}\right)^{\frac {1}{2}}$

where the Hertz contact force$F^{H}$is given by

$F^{H}={\frac {4E^{*}a^{3}}{3R}}$

The penetration due to elastic compression is

$d^{H}={\frac {a^{2}}{R}}$

The vertical displacement at$r=c$is

$u^{H}(c)={\cfrac {1}{\pi R}}\left[a^{2}\left(2-m^{2}\right)\sin ^{-1}\left({\frac {1}{m}}\right)+a^{2}{\sqrt {m^{2}-1}}\right]$

and the separation between the two surfaces at$r=c$is

$h^{H}(c)={\frac {c^{2}}{2R}}-d^{H}+u^{H}(c)$

The surface traction distribution due to the adhesive Dugdale stress is

$p^{D}(r)={\begin{cases}-{\frac {\sigma _{0}}{\pi }}\cos ^{-1}\left[{\frac {2-m^{2}-{\frac {r^{2}}{a^{2}}}}{m^{2}\left(1-{\frac {r^{2}}{m^{2}a^{2}}}\right)}}\right]&\quad {\text{for}}\quad r\leq a\\-\sigma _{0}&\quad {\text{for}}\quad a\leq r\leq c\end{cases}}$

The total adhesive force is then given by

$F^{D}=-2\sigma _{0}m^{2}a^{2}\left[\cos ^{-1}\left({\frac {1}{m}}\right)+{\frac {1}{m^{2}}}{\sqrt {m^{2}-1}}\right]$

The compression due to Dugdale adhesion is

$d^{D}=-\left({\frac {2\sigma _{0}a}{E^{*}}}\right){\sqrt {m^{2}-1}}$

and the gap at$r=c$is

$h^{D}(c)=\left({\frac {4\sigma _{0}a}{\pi E^{*}}}\right)\left[{\sqrt {m^{2}-1}}\cos ^{-1}\left({\frac {1}{m}}\right)+1-m\right]$

The net traction on the contact area is then given by$p(r)=p^{H}(r)+p^{D}(r)$and the net contact force is$F=F^{H}+F^{D}$.When$h(c)=h^{H}(c)+h^{D}(c)=h_{0}$the adhesive traction drops to zero.

Non-dimensionalized values of$a,c,F,d$are introduced at this stage that are defied as

${\bar {a}}=\alpha a~;~~{\bar {c}}:=\alpha c~;~~{\bar {d}}:=\alpha ^{2}Rd~;~~\alpha:=\left({\frac {4E^{*}}{3\pi \Delta \gamma R^{2}}}\right)^{\frac {1}{3}}~;~~{\bar {A}}:=\pi c^{2}~;~~{\bar {F}}={\frac {F}{\pi \Delta \gamma R}}$

In addition, Maugis proposed a parameter$\lambda$which is equivalent to the Tabor parameter$\mu$.This parameter is defined as

$\lambda:=\sigma _{0}\left({\frac {9R}{2\pi \Delta \gamma {E^{*}}^{2}}}\right)^{\frac {1}{3}}\approx 1.16\mu$

where the step cohesive stress$\sigma _{0}$equals to the theoretical stress of the Lennard-Jones potential

$\sigma _{\text{th}}={\frac {16\Delta \gamma }{9{\sqrt {3}}z_{0}}}$

Zheng and Yusuggested another value for the step cohesive stress

$\sigma _{0}=\exp \left(-{\frac {223}{420}}\right)\cdot {\frac {\Delta \gamma }{z_{0}}}\approx 0.588{\frac {\Delta \gamma }{z_{0}}}$

to match the Lennard-Jones potential, which leads to

$\lambda \approx 0.663\mu$

Then the net contact force may be expressed as

${\bar {F}}={\bar {a}}^{3}-\lambda {\bar {a}}^{2}\left[{\sqrt {m^{2}-1}}+m^{2}\sec ^{-1}m\right]$

and the elastic compression as

${\bar {d}}={\bar {a}}^{2}-{\frac {4}{3}}~\lambda {\bar {a}}{\sqrt {m^{2}-1}}$

The equation for the cohesive gap between the two bodies takes the form

${\frac {\lambda {\bar {a}}^{2}}{2}}\left[\left(m^{2}-2\right)\sec ^{-1}m+{\sqrt {m^{2}-1}}\right]+{\frac {4\lambda {\bar {a}}}{3}}\left[{\sqrt {m^{2}-1}}\sec ^{-1}m-m+1\right]=1$

This equation can be solved to obtain values of$c$for various values of$a$and$\lambda$.For large values of$\lambda$,$m\rightarrow 1$and the JKR model is obtained. For small values of$\lambda$the DMT model is retrieved.

Carpick-Ogletree-Salmeron (COS) model

The Maugis-Dugdale model can only be solved iteratively if the value of$\lambda$is not known a-priori. The Carpick-Ogletree-Salmeron approximate solutionsimplifies the process by using the following relation to determine the contact radius$a$:

$a=a_{0}(\beta )\left({\frac {\beta +{\sqrt {1-F/F_{c}(\beta )}}}{1+\beta }}\right)^{\frac {2}{3}}$

where$a_{0}$is the contact area at zero load, and$\beta$is a transition parameter that is related to$\lambda$by

$\lambda \approx -0.924\ln(1-1.02\beta )$

The case$\beta =1$corresponds exactly to JKR theory while$\beta =0$corresponds to DMT theory. For intermediate cases$0<\beta <1$the COS model corresponds closely to the Maugis-Dugdale solution for$0.1<\lambda <5$.

Influence of contact shape

Even in the presence of perfectly smooth surfaces, geometry can come into play in form of the macroscopic shape of the contacting region. When a rigid punch with flat but oddly shaped face is carefully pulled off its soft counterpart, its detachment occurs not instantaneously but detachment fronts start at pointed corners and travel inwards, until the final configuration is reached which for macroscopically isotropic shapes is almost circular. The main parameter determining the adhesive strength of flat contacts occurs to be the maximum linear size of the contact.The process of detachment can as observed experimentally can be seen in the film.

See also

• Adhesive– Non-metallic material used to bond various materials together
• Adhesive bonding– Joining technique used in manufacture and repair
• Adhesion railway– Railway relying on adhesion to move trains
• Adhesive surface forces– Molecular property
• Bearing capacity– Capacity of soil to support loads
• Collision– Instance of two or more bodies physically contacting each other within a short period of time
• Contact dynamics– Motion of multibody systems
• Contact resistance– Electrical resistance attributed to contacting interfaces (ECR)
• Dispersive adhesion– Adhesion between materials due to intermolecular interactions
• Electrostatic generator– Device that generates electrical charge on a high voltage electrode
• Energetically modified cement– Class of cements, mechanically processed to transform reactivity
• Frictional contact mechanics– Study of the deformation of bodies in the presence of frictional effects
• Friction drive– Mechanical power transmission by friction between components
• Galling– Form of wear caused by adhesion between sliding surfaces
• Goniometer– Angle measuring instrument
• Non-smooth mechanics– Modeling approach in mechanics
• Plastic wrap– Thin plastic film used for sealing food
• Rolling (metalworking)– Metal forming process
• Shock (mechanics)– Sudden transient acceleration
• Signorini problem– Elastostatics problem in linear elasticity
• Surface tension– Tendency of a liquid surface to shrink to reduce surface area
• Tribology– Science and engineering of interacting surfaces in relative motion
• Unilateral contact– Mechanical constraint which prevents penetration between two bodies
• Wetting– Ability of a liquid to maintain contact with a solid surface

References

See Also:Contact Mechanics for Soft Hemi-Elliptical Fingertip

External links

• [1]:More about contact stresses and the evolution of bearing stress equations can be found in this publication by NASA Glenn Research Center head the NASA Bearing, Gearing and Transmission Section, Erwin Zaretsky.
• [2]:A MATLAB routine to solve the linear elastic contact mechanics problem entitled; "An LCP solution of the linear elastic contact mechanics problem" is provided at the file exchange at MATLAB Central.
• [3]:Contact mechanics calculator.
• [4]:detailed calculations and formulae of JKR theory for two spheres.
• [5]:A Matlab code for Hertz contact analysis (includes line, point and elliptical cases).
• [6]:JKR, MD, and DMT models of adhesion (Matlab routines).