Probability distribution

For other uses, seeDistribution.

Inprobability theoryandstatistics,aprobability distributionis the mathematicalfunctionthat gives the probabilities of occurrence of possibleoutcomesfor anexperiment.It is a mathematical description of arandomphenomenon in terms of itssample spaceand theprobabilitiesofevents(subsetsof the sample space).

For instance, ifXis used to denote the outcome of a coin toss ( "the experiment" ), then the probability distribution ofXwould take the value 0.5 (1 in 2 or 1/2) forX= heads,and 0.5 forX= tails(assuming thatthe coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values.

Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names.

Introduction

A probability distribution is a mathematical description of the probabilities of events, subsets of thesample space.The sample space, often represented in notation by$\ \Omega \,$is thesetof all possibleoutcomesof a random phenomenon being observed. The sample space may be any set: a set ofreal numbers,a set of descriptive labels, a set ofvectors,a set of arbitrary non-numerical values, etc. For example, the sample space of a coin flip could be Ω ={"heads", "tails"}.

To define probability distributions for the specific case ofrandom variables(so the sample space can be seen as a numeric set), it is common to distinguish betweendiscreteandabsolutely continuousrandom variables.In the discrete case, it is sufficient to specify aprobability mass function$\ p\$assigning a probability to each possible outcome (e.g. when throwing a fairdie,each of the six digits“1”to“6”,corresponding to the number of dots on the die, has the probability$\ {\tfrac {1}{6}}~).$The probability of aneventis then defined to be the sum of the probabilities of all outcomes that satisfy the event; for example, the probability of the event "the die rolls an even value" is $$\ p({\text{ “}}2{\text{” }})+p({\text{ “}}4{\text{” }})+p({\text{ “}}6{\text{” }})={\tfrac {1}{6}}+{\tfrac {1}{6}}+{\tfrac {1}{6}}={\tfrac {1}{2}}~.$$

In contrast, when a random variable takes values from a continuum then by convention, any individual outcome is assigned probability zero. For suchcontinuous random variables,only events that include infinitely many outcomes such as intervals have probability greater than 0.

For example, consider measuring the weight of a piece of ham in the supermarket, and assume the scale can provide arbitrarily many digits of precision. Then, the probability that it weighsexactly500gmust be zero because no matter how high the level of precision chosen, it cannot be assumed the there are no non-zero decimal digits in the remaining omitted digits ignored by the precision level.

However, for the same use case, it is possible to meet quality control requirements such as that a package of "500 g" of ham must weigh between 490 g and 510 g with at least 98% probability. This is possible because this measurement does not require as much precision from the underlying equipment.

Figure 1: The left graph shows a probability density function. The right graph shows the cumulative distribution function. The value atain the cumulative distribution equals the area under the probability density curve up to the pointa.

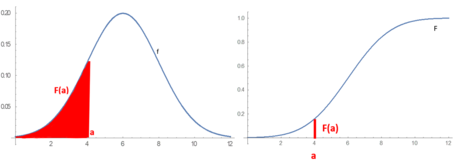
Absolutely continuous probability distributions can be described in several ways. Theprobability density functiondescribes theinfinitesimalprobability of any given value, and the probability that the outcome lies in a given interval can be computed byintegratingthe probability density function over that interval.An alternative description of the distribution is by means of thecumulative distribution function,which describes the probability that the random variable is no larger than a given value (i.e.,$\ {\boldsymbol {\mathcal {P}}}(X<x)\$for some$\ x\$).The cumulative distribution function is the area under theprobability density functionfrom$\ -\infty \$to$\ x\,$as shown in figure 1.

General probability definition

A probability distribution can be described in various forms, such as by a probability mass function or a cumulative distribution function. One of the most general descriptions, which applies for absolutely continuous and discrete variables, is by means of a probability function$P\colon {\mathcal {A}}\to \mathbb {R}$whoseinput space${\mathcal {A}}$is aσ-algebra,and gives areal numberprobabilityas its output, particularly, a number in$[0,1]\subseteq \mathbb {R}$.

The probability function$P$can take as argument subsets of the sample space itself, as in the coin toss example, where the function$P$was defined so thatP(heads) = 0.5andP(tails) = 0.5.However, because of the widespread use ofrandom variables,which transform the sample space into a set of numbers (e.g.,$\mathbb {R}$,$\mathbb {N}$), it is more common to study probability distributions whose argument are subsets of these particular kinds of sets (number sets),and all probability distributions discussed in this article are of this type. It is common to denote as$P(X\in E)$the probability that a certain value of the variable$X$belongs to a certain event$E$.

The above probability function only characterizes a probability distribution if it satisfies all theKolmogorov axioms,that is:

1. $P(X\in E)\geq 0\;\forall E\in {\mathcal {A}}$,so the probability is non-negative
2. $P(X\in E)\leq 1\;\forall E\in {\mathcal {A}}$,so no probability exceeds$1$
3. $P(X\in \bigcup _{i}E_{i})=\sum _{i}P(X\in E_{i})$for any countable disjoint family of sets$\{E_{i}\}$

The concept of probability function is made more rigorous by defining it as the element of aprobability space$(X,{\mathcal {A}},P)$,where$X$is the set of possible outcomes,${\mathcal {A}}$is the set of all subsets$E\subset X$whose probability can be measured, and$P$is the probability function, orprobability measure,that assigns a probability to each of these measurable subsets$E\in {\mathcal {A}}$.

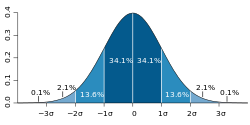
Probability distributions usually belong to one of two classes. Adiscrete probability distributionis applicable to the scenarios where the set of possible outcomes isdiscrete(e.g. a coin toss, a roll of a die) and the probabilities are encoded by a discrete list of the probabilities of the outcomes; in this case the discrete probability distribution is known asprobability mass function.On the other hand,absolutely continuous probability distributionsare applicable to scenarios where the set of possible outcomes can take on values in a continuous range (e.g. real numbers), such as the temperature on a given day. In the absolutely continuous case, probabilities are described by aprobability density function,and the probability distribution is by definition the integral of the probability density function.Thenormal distributionis a commonly encountered absolutely continuous probability distribution. More complex experiments, such as those involvingstochastic processesdefined incontinuous time,may demand the use of more generalprobability measures.

A probability distribution whose sample space is one-dimensional (for example real numbers, list of labels, ordered labels or binary) is calledunivariate,while a distribution whose sample space is avector spaceof dimension 2 or more is calledmultivariate.A univariate distribution gives the probabilities of a singlerandom variabletaking on various different values; a multivariate distribution (ajoint probability distribution) gives the probabilities of arandom vector– a list of two or more random variables – taking on various combinations of values. Important and commonly encountered univariate probability distributions include thebinomial distribution,thehypergeometric distribution,and thenormal distribution.A commonly encountered multivariate distribution is themultivariate normal distribution.

Besides the probability function, the cumulative distribution function, the probability mass function and the probability density function, themoment generating functionand thecharacteristic functionalso serve to identify a probability distribution, as they uniquely determine an underlying cumulative distribution function.

Figure 2: Theprobability density function(pdf) of thenormal distribution,also called Gaussian or "bell curve", the most important absolutely continuous random distribution. As notated on the figure, the probabilities of intervals of values correspond to the area under the curve.

Terminology

Some key concepts and terms, widely used in the literature on the topic of probability distributions, are listed below.

Basic terms

• Random variable:takes values from a sample space; probabilities describe which values and set of values are taken more likely.
• Event:set of possible values (outcomes) of a random variable that occurs with a certain probability.
• Probability functionorprobability measure:describes the probability$P(X\in E)$that the event$E,$occurs.
• Cumulative distribution function:function evaluating theprobabilitythat$X$will take a value less than or equal to$x$for a random variable (only for real-valued random variables).
• Quantile function:the inverse of the cumulative distribution function. Gives$x$such that, with probability$q$,$X$will not exceed$x$.

Discrete probability distributions

• Discrete probability distribution:for many random variables with finitely or countably infinitely many values.
• Probability mass function(pmf): function that gives the probability that a discrete random variable is equal to some value.
• Frequency distribution:a table that displays the frequency of various outcomesin a sample.
• Relative frequencydistribution:afrequency distributionwhere each value has been divided (normalized) by a number of outcomes in asample(i.e. sample size).
• Categorical distribution:for discrete random variables with a finite set of values.

Absolutely continuous probability distributions

• Absolutely continuous probability distribution:for many random variables with uncountably many values.
• Probability density function(pdf) orprobability density:function whose value at any given sample (or point) in thesample space(the set of possible values taken by the random variable) can be interpreted as providing arelative likelihoodthat the value of the random variable would equal that sample.

Related terms

• Support:set of values that can be assumed with non-zero probability (or probability density in the case of a continuous distribution) by the random variable. For a random variable$X$,it is sometimes denoted as$R_{X}$.
• Tail:the regions close to the bounds of the random variable, if the pmf or pdf are relatively low therein. Usually has the form$X>a$,$X<b$or a union thereof.
• Head:the region where the pmf or pdf is relatively high. Usually has the form$a<X<b$.
• Expected valueormean:theweighted averageof the possible values, using their probabilities as their weights; or the continuous analog thereof.
• Median:the value such that the set of values less than the median, and the set greater than the median, each have probabilities no greater than one-half.
• Mode:for a discrete random variable, the value with highest probability; for an absolutely continuous random variable, a location at which the probability density function has a local peak.
• Quantile:the q-quantile is the value$x$such that$P(X<x)=q$.
• Variance:the second moment of the pmf or pdf about the mean; an important measure of thedispersionof the distribution.
• Standard deviation:the square root of the variance, and hence another measure of dispersion.
• Symmetry:a property of some distributions in which the portion of the distribution to the left of a specific value (usually the median) is a mirror image of the portion to its right.
• Skewness:a measure of the extent to which a pmf or pdf "leans" to one side of its mean. The thirdstandardized momentof the distribution.
• Kurtosis:a measure of the "fatness" of the tails of a pmf or pdf. The fourth standardized moment of the distribution.

Cumulative distribution function

In the special case of a real-valued random variable, the probability distribution can equivalently be represented by a cumulative distribution function instead of a probability measure. The cumulative distribution function of a random variable$X$with regard to a probability distribution$p$is defined as $$F(x)=P(X\leq x).$$

The cumulative distribution function of any real-valued random variable has the properties:

• $F(x)$is non-decreasing;
• $F(x)$isright-continuous;
• $0\leq F(x)\leq 1$;
• $\lim _{x\to -\infty }F(x)=0$and$\lim _{x\to \infty }F(x)=1$;and
• $\Pr(a<X\leq b)=F(b)-F(a)$.

Conversely, any function$F:\mathbb {R} \to \mathbb {R}$that satisfies the first four of the properties above is the cumulative distribution function of some probability distribution on the real numbers.

Any probability distribution can be decomposed as themixtureof adiscrete,anabsolutely continuousand asingular continuous distribution,and thus any cumulative distribution function admits a decomposition as theconvex sumof the three according cumulative distribution functions.

Discrete probability distribution

Main article:Probability mass function

Figure 3: Theprobability mass function(pmf)$p(S)$specifies the probability distribution for the sum$S$of counts from twodice.For example, the figure shows that$p(11)=2/36=1/18$.The pmf allows the computation of probabilities of events such as$P(X>9)=1/12+1/18+1/36=1/6$,and all other probabilities in the distribution.

Figure 4: The probability mass function of a discrete probability distribution. The probabilities of thesingletons{1}, {3}, and {7} are respectively 0.2, 0.5, 0.3. A set not containing any of these points has probability zero.

Figure 5: Thecdfof a discrete probability distribution,...

Figure 6:... of a continuous probability distribution,...

Figure 7:... of a distribution which has both a continuous part and a discrete part

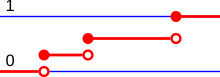
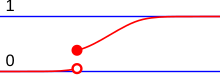
Adiscrete probability distributionis the probability distribution of a random variable that can take on only a countable number of values(almost surely)which means that the probability of any event$E$can be expressed as a (finite orcountably infinite) sum: $$P(X\in E)=\sum _{\omega \in A\cap E}P(X=\omega ),$$ where$A$is a countable set with$P(X\in A)=1$.Thus the discrete random variables (i.e. random variables whose probability distribution is discrete) are exactly those with aprobability mass function$p(x)=P(X=x)$.In the case where the range of values is countably infinite, these values have to decline to zero fast enough for the probabilities to add up to 1. For example, if$p(n)={\tfrac {1}{2^{n}}}$for$n=1,2,...$,the sum of probabilities would be$1/2+1/4+1/8+\dots =1$.

Well-known discrete probability distributions used in statistical modeling include thePoisson distribution,theBernoulli distribution,thebinomial distribution,thegeometric distribution,thenegative binomial distributionandcategorical distribution.When asample(a set of observations) is drawn from a larger population, the sample points have anempirical distributionthat is discrete, and which provides information about the population distribution. Additionally, thediscrete uniform distributionis commonly used in computer programs that make equal-probability random selections between a number of choices.

Cumulative distribution function

A real-valued discrete random variable can equivalently be defined as a random variable whose cumulative distribution function increases only byjump discontinuities—that is, its cdf increases only where it "jumps" to a higher value, and is constant in intervals without jumps. The points where jumps occur are precisely the values which the random variable may take. Thus the cumulative distribution function has the form $$F(x)=P(X\leq x)=\sum _{\omega \leq x}p(\omega ).$$

The points where the cdf jumps always form a countable set; this may be any countable set and thus may even be dense in the real numbers.

Dirac delta representation

A discrete probability distribution is often represented withDirac measures,the probability distributions ofdeterministic random variables.For any outcome$\omega$,let$\delta _{\omega }$be the Dirac measure concentrated at$\omega$.Given a discrete probability distribution, there is a countable set$A$with$P(X\in A)=1$and a probability mass function$p$.If$E$is any event, then $$P(X\in E)=\sum _{\omega \in A}p(\omega )\delta _{\omega }(E),$$or in short,$$P_{X}=\sum _{\omega \in A}p(\omega )\delta _{\omega }.$$

Similarly, discrete distributions can be represented with theDirac delta functionas ageneralizedprobability density function$f$,where$$f(x)=\sum _{\omega \in A}p(\omega )\delta (x-\omega ),$$which means $$P(X\in E)=\int _{E}f(x)\,dx=\sum _{\omega \in A}p(\omega )\int _{E}\delta (x-\omega )=\sum _{\omega \in A\cap E}p(\omega )$$for any event$E.$

Indicator-function representation

For a discrete random variable$X$,let$u_{0},u_{1},\dots$be the values it can take with non-zero probability. Denote

$$\Omega _{i}=X^{-1}(u_{i})=\{\omega:X(\omega )=u_{i}\},\,i=0,1,2,\dots$$

These aredisjoint sets,and for such sets

$$P\left(\bigcup _{i}\Omega _{i}\right)=\sum _{i}P(\Omega _{i})=\sum _{i}P(X=u_{i})=1.$$

It follows that the probability that$X$takes any value except for$u_{0},u_{1},\dots$is zero, and thus one can write$X$as

$$X(\omega )=\sum _{i}u_{i}1_{\Omega _{i}}(\omega )$$

except on a set of probability zero, where$1_{A}$is the indicator function of$A$.This may serve as an alternative definition of discrete random variables.

One-point distribution

A special case is the discrete distribution of a random variable that can take on only one fixed value; in other words, it is adeterministic distribution.Expressed formally, the random variable$X$has a one-point distribution if it has a possible outcome$x$such that$P(X{=}x)=1.$All other possible outcomes then have probability 0. Its cumulative distribution function jumps immediately from 0 to 1.

Absolutely continuous probability distribution

Main article:Probability density function

Anabsolutely continuous probability distributionis a probability distribution on the real numbers with uncountably many possible values, such as a whole interval in the real line, and where the probability of any event can be expressed as an integral.More precisely, a real random variable$X$has anabsolutely continuousprobability distribution if there is a function$f:\mathbb {R} \to [0,\infty ]$such that for each interval$I=[a,b]\subset \mathbb {R}$the probability of$X$belonging to$I$is given by the integral of$f$over$I$: $$P\left(a\leq X\leq b\right)=\int _{a}^{b}f(x)\,dx.$$ This is the definition of aprobability density function,so that absolutely continuous probability distributions are exactly those with a probability density function. In particular, the probability for$X$to take any single value$a$(that is,$a\leq X\leq a$) is zero, because anintegralwith coinciding upper and lower limits is always equal to zero. If the interval$[a,b]$is replaced by any measurable set$A$,the according equality still holds: $$P(X\in A)=\int _{A}f(x)\,dx.$$

Anabsolutely continuous random variableis a random variable whose probability distribution is absolutely continuous.

There are many examples of absolutely continuous probability distributions:normal,uniform,chi-squared,andothers.

Cumulative distribution function

Absolutely continuous probability distributions as defined above are precisely those with anabsolutely continuouscumulative distribution function. In this case, the cumulative distribution function$F$has the form $$F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)\,dt$$ where$f$is a density of the random variable$X$with regard to the distribution$P$.

Note on terminology:Absolutely continuous distributions ought to be distinguished fromcontinuous distributions,which are those having a continuous cumulative distribution function. Every absolutely continuous distribution is a continuous distribution but the inverse is not true, there existsingular distributions,which are neither absolutely continuous nor discrete nor a mixture of those, and do not have a density. An example is given by theCantor distribution.Some authors however use the term "continuous distribution" to denote all distributions whose cumulative distribution function isabsolutely continuous,i.e. refer to absolutely continuous distributions as continuous distributions.

For a more general definition of density functions and the equivalent absolutely continuous measures seeabsolutely continuous measure.

Kolmogorov definition

Main articles:Probability spaceandProbability measure

In themeasure-theoreticformalization ofprobability theory,arandom variableis defined as ameasurable function$X$from aprobability space$(\Omega,{\mathcal {F}},\mathbb {P} )$to ameasurable space$({\mathcal {X}},{\mathcal {A}})$.Given that probabilities of events of the form$\{\omega \in \Omega \mid X(\omega )\in A\}$satisfyKolmogorov's probability axioms,theprobability distribution of$X$is theimage measure$X_{*}\mathbb {P}$of$X$,which is aprobability measureon$({\mathcal {X}},{\mathcal {A}})$satisfying$X_{*}\mathbb {P} =\mathbb {P} X^{-1}$.

Other kinds of distributions

Figure 8: One solution for theRabinovich–Fabrikant equations.What is the probability of observing a state on a certain place of the support (i.e., the red subset)?

Absolutely continuous and discrete distributions with support on$\mathbb {R} ^{k}$or$\mathbb {N} ^{k}$are extremely useful to model a myriad of phenomena,since most practical distributions are supported on relatively simple subsets, such ashypercubesorballs.However, this is not always the case, and there exist phenomena with supports that are actually complicated curves$\gamma:[a,b]\rightarrow \mathbb {R} ^{n}$within some space$\mathbb {R} ^{n}$or similar. In these cases, the probability distribution is supported on the image of such curve, and is likely to be determined empirically, rather than finding a closed formula for it.

One example is shown in the figure to the right, which displays the evolution of asystem of differential equations(commonly known as theRabinovich–Fabrikant equations) that can be used to model the behaviour ofLangmuir wavesinplasma.When this phenomenon is studied, the observed states from the subset are as indicated in red. So one could ask what is the probability of observing a state in a certain position of the red subset; if such a probability exists, it is called the probability measure of the system.

This kind of complicated support appears quite frequently indynamical systems.It is not simple to establish that the system has a probability measure, and the main problem is the following. Let$t_{1}\ll t_{2}\ll t_{3}$be instants in time and$O$a subset of the support; if the probability measure exists for the system, one would expect the frequency of observing states inside set$O$would be equal in interval$[t_{1},t_{2}]$and$[t_{2},t_{3}]$,which might not happen; for example, it could oscillate similar to a sine,$\sin(t)$,whose limit when$t\rightarrow \infty$does not converge. Formally, the measure exists only if the limit of the relative frequency converges when the system is observed into the infinite future.The branch of dynamical systems that studies the existence of a probability measure isergodic theory.

Note that even in these cases, the probability distribution, if it exists, might still be termed "absolutely continuous" or "discrete" depending on whether the support is uncountable or countable, respectively.

Random number generation

Main article:Pseudo-random number sampling

Most algorithms are based on apseudorandom number generatorthat produces numbers$X$that are uniformly distributed in thehalf-open interval[0, 1).Theserandom variates$X$are then transformed via some algorithm to create a new random variate having the required probability distribution. With this source of uniform pseudo-randomness, realizations of any random variable can be generated.

For example, suppose$U$has a uniform distribution between 0 and 1. To construct a random Bernoulli variable for some$0<p<1$,we define $$X={\begin{cases}1,&{\text{if }}U<p\\0,&{\text{if }}U\geq p\end{cases}}$$ so that $$\Pr(X=1)=\Pr(U<p)=p,\quad \Pr(X=0)=\Pr(U\geq p)=1-p.$$

This random variableXhas a Bernoulli distribution with parameter$p$.This is a transformation of discrete random variable.

For a distribution function$F$of an absolutely continuous random variable, an absolutely continuous random variable must be constructed.$F^{\mathit {inv}}$,an inverse function of$F$,relates to the uniform variable$U$: $${U\leq F(x)}={F^{\mathit {inv}}(U)\leq x}.$$

For example, suppose a random variable that has an exponential distribution$F(x)=1-e^{-\lambda x}$must be constructed.

$${\begin{aligned}F(x)=u&\Leftrightarrow 1-e^{-\lambda x}=u\\[2pt]&\Leftrightarrow e^{-\lambda x}=1-u\\[2pt]&\Leftrightarrow -\lambda x=\ln(1-u)\\[2pt]&\Leftrightarrow x={\frac {-1}{\lambda }}\ln(1-u)\end{aligned}}$$ so$F^{\mathit {inv}}(u)={\frac {-1}{\lambda }}\ln(1-u)$and if$U$has a$U(0,1)$distribution, then the random variable$X$is defined by$X=F^{\mathit {inv}}(U)={\frac {-1}{\lambda }}\ln(1-U)$.This has an exponential distribution of$\lambda$.

A frequent problem in statistical simulations (theMonte Carlo method) is the generation ofpseudo-random numbersthat are distributed in a given way.

Common probability distributions and their applications

For a more comprehensive list, seeList of probability distributions.

The concept of the probability distribution and the random variables which they describe underlies the mathematical discipline of probability theory, and the science of statistics. There is spread or variability in almost any value that can be measured in a population (e.g. height of people, durability of a metal, sales growth, traffic flow, etc.); almost all measurements are made with some intrinsic error; in physics, many processes are described probabilistically, from thekinetic properties of gasesto thequantum mechanicaldescription offundamental particles.For these and many other reasons, simplenumbersare often inadequate for describing a quantity, while probability distributions are often more appropriate.

The following is a list of some of the most common probability distributions, grouped by the type of process that they are related to. For a more complete list, seelist of probability distributions,which groups by the nature of the outcome being considered (discrete, absolutely continuous, multivariate, etc.)

All of the univariate distributions below are singly peaked; that is, it is assumed that the values cluster around a single point. In practice, actually observed quantities may cluster around multiple values. Such quantities can be modeled using amixture distribution.

Linear growth (e.g. errors, offsets)

• Normal distribution(Gaussian distribution), for a single such quantity; the most commonly used absolutely continuous distribution

Exponential growth (e.g. prices, incomes, populations)

• Log-normal distribution,for a single such quantity whose log isnormallydistributed
• Pareto distribution,for a single such quantity whose log isexponentiallydistributed; the prototypicalpower lawdistribution

Uniformly distributed quantities

• Discrete uniform distribution,for a finite set of values (e.g. the outcome of a fair dice)
• Continuous uniform distribution,for absolutely continuously distributed values

Bernoulli trials (yes/no events, with a given probability)

• Basic distributions:
  • Bernoulli distribution,for the outcome of a single Bernoulli trial (e.g. success/failure, yes/no)
  • Binomial distribution,for the number of "positive occurrences" (e.g. successes, yes votes, etc.) given a fixed total number ofindependentoccurrences
  • Negative binomial distribution,for binomial-type observations but where the quantity of interest is the number of failures before a given number of successes occurs
  • Geometric distribution,for binomial-type observations but where the quantity of interest is the number of failures before the first success; a special case of thenegative binomial distribution
• Related to sampling schemes over a finite population:
  • Hypergeometric distribution,for the number of "positive occurrences" (e.g. successes, yes votes, etc.) given a fixed number of total occurrences, usingsampling without replacement
  • Beta-binomial distribution,for the number of "positive occurrences" (e.g. successes, yes votes, etc.) given a fixed number of total occurrences, sampling using aPólya urn model(in some sense, the "opposite" ofsampling without replacement)

Categorical outcomes (events withKpossible outcomes)

• Categorical distribution,for a single categorical outcome (e.g. yes/no/maybe in a survey); a generalization of theBernoulli distribution
• Multinomial distribution,for the number of each type of categorical outcome, given a fixed number of total outcomes; a generalization of thebinomial distribution
• Multivariate hypergeometric distribution,similar to themultinomial distribution,but usingsampling without replacement;a generalization of thehypergeometric distribution

Poisson process (events that occur independently with a given rate)

• Poisson distribution,for the number of occurrences of a Poisson-type event in a given period of time
• Exponential distribution,for the time before the next Poisson-type event occurs
• Gamma distribution,for the time before the next k Poisson-type events occur

Absolute values of vectors with normally distributed components

• Rayleigh distribution,for the distribution of vector magnitudes with Gaussian distributed orthogonal components. Rayleigh distributions are found in RF signals with Gaussian real and imaginary components.
• Rice distribution,a generalization of the Rayleigh distributions for where there is a stationary background signal component. Found inRician fadingof radio signals due to multipath propagation and in MR images with noise corruption on non-zero NMR signals.

Normally distributed quantities operated with sum of squares

• Chi-squared distribution,the distribution of a sum of squaredstandard normalvariables; useful e.g. for inference regarding thesample varianceof normally distributed samples (seechi-squared test)
• Student's t distribution,the distribution of the ratio of astandard normalvariable and the square root of a scaledchi squaredvariable; useful for inference regarding themeanof normally distributed samples with unknown variance (seeStudent's t-test)
• F-distribution,the distribution of the ratio of two scaledchi squaredvariables; useful e.g. for inferences that involve comparing variances or involvingR-squared(the squaredcorrelation coefficient)

As conjugate prior distributions in Bayesian inference

Main article:Conjugate prior

• Beta distribution,for a single probability (real number between 0 and 1); conjugate to theBernoulli distributionandbinomial distribution
• Gamma distribution,for a non-negative scaling parameter; conjugate to the rate parameter of aPoisson distributionorexponential distribution,theprecision(inversevariance) of anormal distribution,etc.
• Dirichlet distribution,for a vector of probabilities that must sum to 1; conjugate to thecategorical distributionandmultinomial distribution;generalization of thebeta distribution
• Wishart distribution,for a symmetricnon-negative definitematrix; conjugate to the inverse of thecovariance matrixof amultivariate normal distribution;generalization of thegamma distribution

Some specialized applications of probability distributions

• Thecache language modelsand otherstatistical language modelsused innatural language processingto assign probabilities to the occurrence of particular words and word sequences do so by means of probability distributions.
• In quantum mechanics, the probability density of finding the particle at a given point is proportional to the square of the magnitude of the particle'swavefunctionat that point (seeBorn rule). Therefore, the probability distribution function of the position of a particle is described by${\textstyle P_{a\leq x\leq b}(t)=\int _{a}^{b}dx\,|\Psi (x,t)|^{2}}$,probability that the particle's positionxwill be in the intervala≤x≤bin dimension one, and a similartriple integralin dimension three. This is a key principle of quantum mechanics.
• Probabilistic load flow inpower-flow studyexplains the uncertainties of input variables as probability distribution and provides the power flow calculation also in term of probability distribution.
• Prediction of natural phenomena occurrences based on previousfrequency distributionssuch astropical cyclones,hail, time in between events, etc.

Fitting

This section is an excerpt fromProbability distribution fitting.[edit]

Probability distribution fittingor simply distribution fitting is the fitting of a probability distribution to a series of data concerning the repeated measurement of a variable phenomenon. The aim of distribution fitting is topredicttheprobabilityor toforecastthefrequencyof occurrence of the magnitude of the phenomenon in a certain interval.

There are many probability distributions (seelist of probability distributions) of which some can be fitted more closely to the observed frequency of the data than others, depending on the characteristics of the phenomenon and of the distribution. The distribution giving a close fit is supposed to lead to good predictions.

In distribution fitting, therefore, one needs to select a distribution that suits the data well.

See also

• Conditional probability distribution
• Empirical probability distribution
• Histogram
• Joint probability distribution
• Probability measure
• Quasiprobability distribution
• Riemann–Stieltjes integral application to probability theory

Lists

• List of probability distributions
• List of statistical topics

References

Sources

• den Dekker, A. J.; Sijbers, J. (2014). "Data distributions in magnetic resonance images: A review".Physica Medica.30(7): 725–741.doi:10.1016/j.ejmp.2014.05.002.PMID25059432.
• Vapnik, Vladimir Naumovich (1998).Statistical Learning Theory.John Wiley and Sons.

External links

• "Probability distribution",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Field Guide to Continuous Probability Distributions,Gavin E. Crooks.
• Distinguishing probability measure, function and distribution,Math Stack Exchange