Curl (mathematics)

"Rotor (operator)" redirects here. For the geometric algebra concept, seeRotor (mathematics).For other uses, seeRotation operator (disambiguation).

Depiction of a two-dimensional vector field with a uniform curl.

Invector calculus,thecurl,also known asrotor,is avector operatorthat describes theinfinitesimalcirculationof avector fieldin three-dimensionalEuclidean space.The curl at a point in the field is represented by avectorwhose length and direction denote themagnitudeand axis of the maximum circulation.The curl of a field is formally defined as the circulation density at each point of the field.

A vector field whose curl is zero is calledirrotational.The curl is a form ofdifferentiationfor vector fields. The corresponding form of thefundamental theorem of calculusisStokes' theorem,which relates thesurface integralof the curl of a vector field to theline integralof the vector field around the boundary curve.

The notationcurlFis more common in North America. In the rest of the world, particularly in 20th century scientific literature, the alternative notationrotFis traditionally used, which comes from the "rate of rotation" that it represents. To avoid confusion, modern authors tend to use thecross productnotation with thedel(nabla) operator, as in$\nabla \times \mathbf {F}$,which also reveals the relation between curl (rotor),divergence,andgradientoperators.

Unlike thegradientanddivergence,curl as formulated in vector calculus does not generalize simply to other dimensions; somegeneralizationsare possible, but only in three dimensions is the geometrically defined curl of a vector field again a vector field. This deficiency is a direct consequence of the limitations of vector calculus; on the other hand, when expressed as an antisymmetric tensor field via the wedge operator ofgeometric calculus,the curl generalizes to all dimensions. The circumstance is similar to that attending the 3-dimensionalcross product,and indeed the connection is reflected in the notation$\nabla \times$for the curl.

The name "curl" was first suggested byJames Clerk Maxwellin 1871but the concept was apparently first used in the construction of an optical field theory byJames MacCullaghin 1839.

Definition

The components ofFat positionr,normal and tangent to a closed curveCin a plane, enclosing a planarvector area$\mathbf {A} =A\mathbf {\hat {n}}$.

Right-hand rule

Convention for vector orientation of the line integral

The thumb points in the direction of$\mathbf {\hat {n}}$and the fingers curl along the orientation ofC

The curl of a vector fieldF,denoted bycurlF,or$\nabla \times \mathbf {F}$,orrotF,is an operator that mapsC^kfunctions inR³toC^k−1functions inR³,and in particular, it maps continuously differentiable functionsR³→R³to continuous functionsR³→R³.It can be defined in several ways, to be mentioned below:

One way to define the curl of a vector field at a point is implicitly through its components along various axes passing through the point: if$\mathbf {\hat {u}}$is any unit vector, the component of the curl ofFalong the direction$\mathbf {\hat {u}}$may be defined to be the limiting value of a closedline integralin a plane perpendicular to$\mathbf {\hat {u}}$divided by the area enclosed, as the path of integration is contracted indefinitely around the point.

More specifically, the curl is defined at a pointpas $$(\nabla \times \mathbf {F} )(p)\cdot \mathbf {\hat {u}} \ {\overset {\underset {\mathrm {def} }{}}{{}={}}}\lim _{A\to 0}{\frac {1}{|A|}}\oint _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {r}$$ where theline integralis calculated along theboundaryCof theareaAin question,|A|being the magnitude of the area. This equation defines the component of the curl ofFalong the direction$\mathbf {\hat {u}}$.The infinitesimal surfaces bounded byChave$\mathbf {\hat {u}}$as theirnormal.Cis oriented via theright-hand rule.

The above formula means that the component of the curl of a vector field along a certain axis is theinfinitesimalarea densityof the circulation of the field in a plane perpendicular to that axis. This formula does nota prioridefine a legitimate vector field, for the individual circulation densities with respect to various axesa priorineed not relate to each other in the same way as the components of a vector do; that theydoindeed relate to each other in this precise manner must be proven separately.

To this definition fits naturally theKelvin–Stokes theorem,as a global formula corresponding to the definition. It equates thesurface integralof the curl of a vector field to the above line integral taken around the boundary of the surface.

Another way one can define the curl vector of a functionFat a point is explicitly as the limiting value of a vector-valued surface integral around a shell enclosingpdivided by the volume enclosed, as the shell is contracted indefinitely aroundp.

More specifically, the curl may be defined by the vector formula $$(\nabla \times \mathbf {F} )(p){\overset {\underset {\mathrm {def} }{}}{{}={}}}\lim _{V\to 0}{\frac {1}{|V|}}\oint _{S}\mathbf {\hat {n}} \times \mathbf {F} \ \mathrm {d} S$$ where the surface integral is calculated along the boundarySof the volumeV,|V|being the magnitude of the volume, and$\mathbf {\hat {n}}$pointing outward from the surfaceSperpendicularly at every point inS.

In this formula, the cross product in the integrand measures the tangential component ofFat each point on the surfaceS,and points along the surface at right angles to thetangential projectionofF.Integrating this cross product over the whole surface results in a vector whose magnitude measures the overall circulation ofFaroundS,and whose direction is at right angles to this circulation. The above formula says that thecurlof a vector field at a point is theinfinitesimal volume densityof this "circulation vector" around the point.

To this definition fits naturally another global formula (similar to the Kelvin-Stokes theorem) which equates thevolume integralof the curl of a vector field to the above surface integral taken over the boundary of the volume.

Whereas the above two definitions of the curl are coordinate free, there is another "easy to memorize" definition of the curl in curvilinearorthogonal coordinates,e.g. inCartesian coordinates,spherical,cylindrical,or evenellipticalorparabolic coordinates:$${\begin{aligned}&(\operatorname {curl} \mathbf {F} )_{1}={\frac {1}{h_{2}h_{3}}}\left({\frac {\partial (h_{3}F_{3})}{\partial u_{2}}}-{\frac {\partial (h_{2}F_{2})}{\partial u_{3}}}\right),\\[5pt]&(\operatorname {curl} \mathbf {F} )_{2}={\frac {1}{h_{3}h_{1}}}\left({\frac {\partial (h_{1}F_{1})}{\partial u_{3}}}-{\frac {\partial (h_{3}F_{3})}{\partial u_{1}}}\right),\\[5pt]&(\operatorname {curl} \mathbf {F} )_{3}={\frac {1}{h_{1}h_{2}}}\left({\frac {\partial (h_{2}F_{2})}{\partial u_{1}}}-{\frac {\partial (h_{1}F_{1})}{\partial u_{2}}}\right).\end{aligned}}$$

The equation for each component(curlF)_kcan be obtained by exchanging each occurrence of a subscript 1, 2, 3 in cyclic permutation: 1 → 2, 2 → 3, and 3 → 1 (where the subscripts represent the relevant indices).

If(x₁,x₂,x₃)are theCartesian coordinatesand(u₁,u₂,u₃)are the orthogonal coordinates, then $$h_{i}={\sqrt {\left({\frac {\partial x_{1}}{\partial u_{i}}}\right)^{2}+\left({\frac {\partial x_{2}}{\partial u_{i}}}\right)^{2}+\left({\frac {\partial x_{3}}{\partial u_{i}}}\right)^{2}}}$$ is the length of the coordinate vector corresponding tou_i.The remaining two components of curl result fromcyclic permutationofindices:3,1,2 → 1,2,3 → 2,3,1.

Usage

In practice, the two coordinate-free definitions described above are rarely used because in virtually all cases, the curloperatorcan be applied using some set ofcurvilinear coordinates,for which simpler representations have been derived.

The notation∇ ×Fhas its origins in the similarities to the 3-dimensionalcross product,and it is useful as amnemonicinCartesian coordinatesif∇is taken as a vectordifferential operatordel.Such notation involvingoperatorsis common inphysicsandalgebra.

Expanded in 3-dimensionalCartesian coordinates(seeDel in cylindrical and spherical coordinatesforsphericalandcylindricalcoordinate representations),∇ ×Fis, forFcomposed of[F_x,F_y,F_z](where the subscripts indicate the components of the vector, not partial derivatives): $$\nabla \times \mathbf {F} ={\begin{vmatrix}{\boldsymbol {\hat {\imath }}}&{\boldsymbol {\hat {\jmath }}}&{\boldsymbol {\hat {k}}}\\[5mu]{\dfrac {\partial }{\partial x}}&{\dfrac {\partial }{\partial y}}&{\dfrac {\partial }{\partial z}}\\[5mu]F_{x}&F_{y}&F_{z}\end{vmatrix}}$$ wherei,j,andkare theunit vectorsfor thex-,y-, andz-axes, respectively. This expands as follows: $$\nabla \times \mathbf {F} =\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right){\boldsymbol {\hat {\imath }}}+\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right){\boldsymbol {\hat {\jmath }}}+\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right){\boldsymbol {\hat {k}}}$$

Although expressed in terms of coordinates, the result is invariant under proper rotations of the coordinate axes but the result inverts under reflection.

In a general coordinate system, the curl is given by $$(\nabla \times \mathbf {F} )^{k}={\frac {1}{\sqrt {g}}}\varepsilon ^{k\ell m}\nabla _{\ell }F_{m}$$ whereεdenotes theLevi-Civita tensor,∇thecovariant derivative,$g$is thedeterminantof themetric tensorand theEinstein summation conventionimplies that repeated indices are summed over. Due to the symmetry of the Christoffel symbols participating in the covariant derivative, this expression reduces to the partial derivative: $$(\nabla \times \mathbf {F} )={\frac {1}{\sqrt {g}}}\mathbf {R} _{k}\varepsilon ^{k\ell m}\partial _{\ell }F_{m}$$ whereR_kare the local basis vectors. Equivalently, using theexterior derivative,the curl can be expressed as: $$\nabla \times \mathbf {F} =\left(\star {\big (}{\mathrm {d} }\mathbf {F} ^{\flat }{\big )}\right)^{\sharp }$$

Here♭and♯are themusical isomorphisms,and★is theHodge star operator.This formula shows how to calculate the curl ofFin any coordinate system, and how to extend the curl to anyorientedthree-dimensionalRiemannianmanifold. Since this depends on a choice of orientation, curl is achiraloperation. In other words, if the orientation is reversed, then the direction of the curl is also reversed.

Examples

Example 1

Suppose the vector field describes thevelocity fieldof afluid flow(such as a large tank ofliquidorgas) and a small ball is located within the fluid or gas (the center of the ball being fixed at a certain point). If the ball has a rough surface, the fluid flowing past it will make it rotate. The rotation axis (oriented according to the right hand rule) points in the direction of the curl of the field at the center of the ball, and the angular speed of the rotation is half the magnitude of the curl at this point. The curl of the vector field at any point is given by the rotation of an infinitesimal area in thexy-plane (forz-axis component of the curl),zx-plane (fory-axis component of the curl) andyz-plane (forx-axis component of the curl vector). This can be seen in the examples below.

Example 2

Vector fieldF(x,y)=[y,−x](left) and its curl (right).

Thevector field $$\mathbf {F} (x,y,z)=y{\boldsymbol {\hat {\imath }}}-x{\boldsymbol {\hat {\jmath }}}$$ can be decomposed as $$F_{x}=y,F_{y}=-x,F_{z}=0.$$

Upon visual inspection, the field can be described as "rotating". If the vectors of the field were to represent a linearforceacting on objects present at that point, and an object were to be placed inside the field, the object would start to rotate clockwise around itself. This is true regardless of where the object is placed.

Calculating the curl: $$\nabla \times \mathbf {F} =0{\boldsymbol {\hat {\imath }}}+0{\boldsymbol {\hat {\jmath }}}+\left({\frac {\partial }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right){\boldsymbol {\hat {k}}}=-2{\boldsymbol {\hat {k}}}$$

The resulting vector field describing the curl would at all points be pointing in the negativezdirection. The results of this equation align with what could have been predicted using theright-hand ruleusing aright-handed coordinate system.Being a uniform vector field, the object described before would have the same rotational intensity regardless of where it was placed.

Example 3

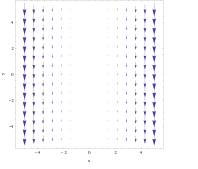
Vector fieldF(x,y) = [0, −x²](left) and its curl (right).

For the vector field $$\mathbf {F} (x,y,z)=-x^{2}{\boldsymbol {\hat {\jmath }}}$$

the curl is not as obvious from the graph. However, taking the object in the previous example, and placing it anywhere on the linex= 3,the force exerted on the right side would be slightly greater than the force exerted on the left, causing it to rotate clockwise. Using the right-hand rule, it can be predicted that the resulting curl would be straight in the negativezdirection. Inversely, if placed onx= −3,the object would rotate counterclockwise and the right-hand rule would result in a positivezdirection.

Calculating the curl: $${\nabla }\times \mathbf {F} =0{\boldsymbol {\hat {\imath }}}+0{\boldsymbol {\hat {\jmath }}}+{\frac {\partial }{\partial x}}\left(-x^{2}\right){\boldsymbol {\hat {k}}}=-2x{\boldsymbol {\hat {k}}}.$$

The curl points in the negativezdirection whenxis positive and vice versa. In this field, the intensity of rotation would be greater as the object moves away from the planex= 0.

Further examples

• In a vector field describing the linear velocities of each part of a rotating disk inuniform circular motion,the curl has the same value at all points, and this value turns out to be exactly two times the vectorialangular velocityof the disk (oriented as usual by theright-hand rule). More generally, for any flowing mass, the linear velocity vector field at each point of the mass flow has a curl (thevorticityof the flow at that point) equal to exactly two times thelocalvectorial angular velocity of the mass about the point.
• For any solid object subject to an external physical force (such as gravity or the electromagnetic force), one may consider the vector field representing the infinitesimal force-per-unit-volume contributions acting at each of the points of the object. This force field may create a nettorqueon the object about its center of mass, and this torque turns out to be directly proportional and vectorially parallel to the (vector-valued) integral of thecurlof the force field over the whole volume.
• Of the fourMaxwell's equations,two—Faraday's lawandAmpère's law—can be compactly expressed using curl. Faraday's law states that the curl of an electric field is equal to the opposite of the time rate of change of the magnetic field, while Ampère's law relates the curl of the magnetic field to the current and the time rate of change of the electric field.

Identities

Main article:Vector calculus identities

In generalcurvilinear coordinates(not only in Cartesian coordinates), the curl of a cross product of vector fieldsvandFcan be shown to be $$\nabla \times \left(\mathbf {v\times F} \right)={\Big (}\left(\mathbf {\nabla \cdot F} \right)+\mathbf {F\cdot \nabla } {\Big )}\mathbf {v} -{\Big (}\left(\mathbf {\nabla \cdot v} \right)+\mathbf {v\cdot \nabla } {\Big )}\mathbf {F} \.$$

Interchanging the vector fieldvand∇operator, we arrive at the cross product of a vector field with curl of a vector field: $$\mathbf {v\ \times } \left(\mathbf {\nabla \times F} \right)=\nabla _{\mathbf {F} }\left(\mathbf {v\cdot F} \right)-\left(\mathbf {v\cdot \nabla } \right)\mathbf {F} \,$$ where∇_Fis the Feynman subscript notation, which considers only the variation due to the vector fieldF(i.e., in this case,vis treated as being constant in space).

Another example is the curl of a curl of a vector field. It can be shown that in general coordinates $$\nabla \times \left(\mathbf {\nabla \times F} \right)=\mathbf {\nabla } (\mathbf {\nabla \cdot F} )-\nabla ^{2}\mathbf {F} \,$$ and this identity defines thevector LaplacianofF,symbolized as∇²F.

The curl of thegradientofanyscalar fieldφis always thezero vectorfield $$\nabla \times (\nabla \varphi )={\boldsymbol {0}}$$ which follows from theantisymmetryin the definition of the curl, and thesymmetry of second derivatives.

Thedivergenceof the curl of any vector field is equal to zero: $$\nabla \cdot (\nabla \times \mathbf {F} )=0.$$

Ifφis a scalar valued function andFis a vector field, then $$\nabla \times (\varphi \mathbf {F} )=\nabla \varphi \times \mathbf {F} +\varphi \nabla \times \mathbf {F}$$

Generalizations

The vector calculus operations ofgrad,curl, anddivare most easily generalized in the context of differential forms, which involves a number of steps. In short, they correspond to the derivatives of 0-forms, 1-forms, and 2-forms, respectively. The geometric interpretation of curl as rotation corresponds to identifyingbivectors(2-vectors) in 3 dimensions with thespecial orthogonal Lie algebra${\mathfrak {so}}(3)$of infinitesimal rotations (in coordinates, skew-symmetric 3 × 3 matrices), while representing rotations by vectors corresponds to identifying 1-vectors (equivalently, 2-vectors) and${\mathfrak {so}}(3)$,these all being 3-dimensional spaces.

Differential forms

Main article:Differential form

In 3 dimensions, a differential 0-form is a real-valued functionf(x,y,z);a differential 1-form is the following expression, where the coefficients are functions: $$a_{1}\,dx+a_{2}\,dy+a_{3}\,dz;$$ a differential 2-form is the formal sum, again with function coefficients: $$a_{12}\,dx\wedge dy+a_{13}\,dx\wedge dz+a_{23}\,dy\wedge dz;$$ and a differential 3-form is defined by a single term with one function as coefficient: $$a_{123}\,dx\wedge dy\wedge dz.$$ (Here thea-coefficients are real functions of three variables; the "wedge products", e.g.dx∧dy,can be interpreted as some kind of oriented area elements,dx∧dy= −dy∧dx,etc.)

Theexterior derivativeof ak-form inR³is defined as the(k+ 1)-form from above—and inRⁿif, e.g., $$\omega ^{(k)}=\sum _{1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n}a_{i_{1},\ldots,i_{k}}\,dx_{i_{1}}\wedge \cdots \wedge dx_{i_{k}},$$ then the exterior derivativedleads to $$d\omega ^{(k)}=\sum _{\scriptstyle {j=1} \atop \scriptstyle {i_{1}<\cdots <i_{k}}}^{n}{\frac {\partial a_{i_{1},\ldots,i_{k}}}{\partial x_{j}}}\,dx_{j}\wedge dx_{i_{1}}\wedge \cdots \wedge dx_{i_{k}}.$$

The exterior derivative of a 1-form is therefore a 2-form, and that of a 2-form is a 3-form. On the other hand, because of the interchangeability of mixed derivatives, $${\frac {\partial ^{2}}{\partial x_{i}\,\partial x_{j}}}={\frac {\partial ^{2}}{\partial x_{j}\,\partial x_{i}}},$$ and antisymmetry, $$dx_{i}\wedge dx_{j}=-dx_{j}\wedge dx_{i}$$

the twofold application of the exterior derivative yields$0$(the zero$k+2$-form).

Thus, denoting the space ofk-forms byΩ^k(R³)and the exterior derivative bydone gets a sequence: $$0\,{\overset {d}{\longrightarrow }}\;\Omega ^{0}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{1}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{2}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\;\Omega ^{3}\left(\mathbb {R} ^{3}\right)\,{\overset {d}{\longrightarrow }}\,0.$$

HereΩ^k(Rⁿ)is the space of sections of theexterior algebraΛ^k(Rⁿ)vector bundleoverRⁿ,whose dimension is thebinomial coefficient(ⁿ
_k);note thatΩ^k(R³) = 0fork> 3ork< 0.Writing only dimensions, one obtains a row ofPascal's triangle:

0 → 1 → 3 → 3 → 1 → 0;

the 1-dimensional fibers correspond to scalar fields, and the 3-dimensional fibers to vector fields, as described below. Modulo suitable identifications, the three nontrivial occurrences of the exterior derivative correspond to grad, curl, and div.

Differential forms and the differential can be defined on any Euclidean space, or indeed any manifold, without any notion of a Riemannian metric. On aRiemannian manifold,or more generallypseudo-Riemannian manifold,k-forms can be identified withk-vectorfields (k-forms arek-covector fields, and a pseudo-Riemannian metric gives an isomorphism between vectors and covectors), and on anorientedvector space with anondegenerate form(an isomorphism between vectors and covectors), there is an isomorphism betweenk-vectors and(n−k)-vectors; in particular on (the tangent space of) an oriented pseudo-Riemannian manifold. Thus on an oriented pseudo-Riemannian manifold, one can interchangek-forms,k-vector fields,(n−k)-forms, and(n−k)-vector fields; this is known asHodge duality.Concretely, onR³this is given by:

• 1-forms and 1-vector fields: the 1-forma_xdx+a_ydy+a_zdzcorresponds to the vector field(a_x,a_y,a_z).
• 1-forms and 2-forms: one replacesdxby the dual quantitydy∧dz(i.e., omitdx), and likewise, taking care of orientation:dycorresponds todz∧dx= −dx∧dz,anddzcorresponds todx∧dy.Thus the forma_xdx+a_ydy+a_zdzcorresponds to the "dual form"a_zdx∧dy+a_ydz∧dx+a_xdy∧dz.

Thus, identifying 0-forms and 3-forms with scalar fields, and 1-forms and 2-forms with vector fields:

• grad takes a scalar field (0-form) to a vector field (1-form);
• curl takes a vector field (1-form) to a pseudovector field (2-form);
• div takes a pseudovector field (2-form) to a pseudoscalar field (3-form)

On the other hand, the fact thatd²= 0corresponds to the identities $$\nabla \times (\nabla f)=\mathbf {0}$$ for any scalar fieldf,and $$\nabla \cdot (\nabla \times \mathbf {v} )=0$$ for any vector fieldv.

Grad and div generalize to all oriented pseudo-Riemannian manifolds, with the same geometric interpretation, because the spaces of 0-forms andn-forms at each point are always 1-dimensional and can be identified with scalar fields, while the spaces of 1-forms and(n− 1)-forms are always fiberwisen-dimensional and can be identified with vector fields.

Curl does not generalize in this way to 4 or more dimensions (or down to 2 or fewer dimensions); in 4 dimensions the dimensions are

0 → 1 → 4 → 6 → 4 → 1 → 0;

so the curl of a 1-vector field (fiberwise 4-dimensional) is a2-vector field,which at each point belongs to 6-dimensional vector space, and so one has $$\omega ^{(2)}=\sum _{i<k=1,2,3,4}a_{i,k}\,dx_{i}\wedge dx_{k},$$ which yields a sum of six independent terms, and cannot be identified with a 1-vector field. Nor can one meaningfully go from a 1-vector field to a 2-vector field to a 3-vector field (4 → 6 → 4), as taking the differential twice yields zero (d²= 0). Thus there is no curl function from vector fields to vector fields in other dimensions arising in this way.

However, one can define a curl of a vector field as a2-vector fieldin general, as described below.

Curl geometrically

2-vectors correspond to the exterior powerΛ²V;in the presence of an inner product, in coordinates these are the skew-symmetric matrices, which are geometrically considered as thespecial orthogonal Lie algebra${\mathfrak {so}}$(V)of infinitesimal rotations. This has(ⁿ
₂)=1/2n(n− 1)dimensions, and allows one to interpret the differential of a 1-vector field as its infinitesimal rotations. Only in 3 dimensions (or trivially in 0 dimensions) we haven=1/2n(n− 1),which is the most elegant and common case. In 2 dimensions the curl of a vector field is not a vector field but a function, as 2-dimensional rotations are given by an angle (a scalar – an orientation is required to choose whether one counts clockwise or counterclockwise rotations as positive); this is not the div, but is rather perpendicular to it. In 3 dimensions the curl of a vector field is a vector field as is familiar (in 1 and 0 dimensions the curl of a vector field is 0, because there are no non-trivial 2-vectors), while in 4 dimensions the curl of a vector field is, geometrically, at each point an element of the 6-dimensional Lie algebra${\mathfrak {so}}(4)$.

The curl of a 3-dimensional vector field which only depends on 2 coordinates (sayxandy) is simply a vertical vector field (in thezdirection) whose magnitude is the curl of the 2-dimensional vector field, as in the examples on this page.

Considering curl as a 2-vector field (an antisymmetric 2-tensor) has been used to generalize vector calculus and associated physics to higher dimensions.

Inverse

Main article:Helmholtz decomposition

In the case where the divergence of a vector fieldVis zero, a vector fieldWexists such thatV= curl(W).This is why themagnetic field,characterized by zero divergence, can be expressed as the curl of amagnetic vector potential.

IfWis a vector field withcurl(W) =V,then adding any gradient vector fieldgrad(f)toWwill result in another vector fieldW+ grad(f)such thatcurl(W+ grad(f)) =Vas well. This can be summarized by saying that the inverse curl of a three-dimensional vector field can be obtained up to an unknownirrotational fieldwith theBiot–Savart law.

See also

• Helmholtz decomposition
• Del in cylindrical and spherical coordinates
• Vorticity

Further reading

• Korn, Granino Arthur andTheresa M. Korn(January 2000).Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review.New York: Dover Publications. pp. 157–160.ISBN0-486-41147-8.
• Schey, H. M. (1997).Div, Grad, Curl, and All That: An Informal Text on Vector Calculus.New York: Norton.ISBN0-393-96997-5.

External links

• "Curl",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• "Multivariable calculus".mathinsight.org.RetrievedFebruary 12,2022.
• "Divergence and Curl: The Language of Maxwell's Equations, Fluid Flow, and More".June 21, 2018.Archivedfrom the original on 2021-11-24 – viaYouTube.