Dual space

Inmathematics,anyvector space$V$has a correspondingdual vector space(or justdual spacefor short) consisting of alllinear formson$V,$together with the vector space structure ofpointwiseaddition and scalar multiplication by constants.

The dual space as defined above is defined for all vector spaces, and to avoid ambiguity may also be called thealgebraic dual space. When defined for atopological vector space,there is a subspace of the dual space, corresponding tocontinuous linear functionals,called thecontinuous dual space.

Dual vector spaces find application in many branches of mathematics that use vector spaces, such as intensoranalysis withfinite-dimensionalvector spaces. When applied to vector spaces of functions (which are typically infinite-dimensional), dual spaces are used to describemeasures,distributions,andHilbert spaces.Consequently, the dual space is an important concept infunctional analysis.

Early terms fordualincludepolarer Raum[Hahn 1927],espace conjugué,adjoint space[Alaoglu 1940], andtransponierter Raum[Schauder 1930] and [Banach 1932]. The termdualis due toBourbaki1938.

Algebraic dual space

Given anyvector space$V$over afield$F$,the(algebraic) dual space$V^{*}$(alternatively denoted by$V^{\lor }$or$V'$)is defined as the set of alllinear maps$\varphi:V\to F$(linear functionals). Since linear maps are vector spacehomomorphisms,the dual space may be denoted$\hom(V,F)$. The dual space$V^{*}$itself becomes a vector space over$F$when equipped with an addition and scalar multiplication satisfying:

${\begin{aligned}(\varphi +\psi )(x)&=\varphi (x)+\psi (x)\\(a\varphi )(x)&=a\left(\varphi (x)\right)\end{aligned}}$

for all$\varphi,\psi \in V^{*}$,$x\in V$,and$a\in F$.

Elements of the algebraic dual space$V^{*}$are sometimes calledcovectors,one-forms,orlinear forms.

The pairing of a functional$\varphi$in the dual space$V^{*}$and an element$x$of$V$is sometimes denoted by a bracket:$\varphi (x)=[x,\varphi ]$ or$\varphi (x)=\langle x,\varphi \rangle$.This pairing defines a nondegeneratebilinear mapping$\langle \cdot,\cdot \rangle:V\times V^{*}\to F$called thenatural pairing.

Finite-dimensional case

See also:Dual basis

If$V$is finite-dimensional, then$V^{*}$has the same dimension as$V$.Given abasis$\{\mathbf {e} _{1},\dots,\mathbf {e} _{n}\}$in$V$,it is possible to construct a specific basis in$V^{*}$,called thedual basis.This dual basis is a set$\{\mathbf {e} ^{1},\dots,\mathbf {e} ^{n}\}$of linear functionals on$V$,defined by the relation

$\mathbf {e} ^{i}(c^{1}\mathbf {e} _{1}+\cdots +c^{n}\mathbf {e} _{n})=c^{i},\quad i=1,\ldots,n$

for any choice of coefficients$c^{i}\in F$.In particular, letting in turn each one of those coefficients be equal to one and the other coefficients zero, gives the system of equations

$\mathbf {e} ^{i}(\mathbf {e} _{j})=\delta _{j}^{i}$

where$\delta _{j}^{i}$is theKronecker deltasymbol. This property is referred to as thebi-orthogonality property.

Proof

Consider$\{\mathbf {e} _{1},\dots,\mathbf {e} _{n}\}$the basis of V. Let$\{\mathbf {e} ^{1},\dots,\mathbf {e} ^{n}\}$be defined as the following: $\mathbf {e} ^{i}(c^{1}\mathbf {e} _{1}+\cdots +c^{n}\mathbf {e} _{n})=c^{i},\quad i=1,\ldots,n$. These are a basis of$V^{*}$because: The$\mathbf {e} ^{i},i=1,2,\dots,n,$are linear functionals, which map$x,y\in V$such as$x=\alpha _{1}\mathbf {e} _{1}+\dots +\alpha _{n}\mathbf {e} _{n}$and$y=\beta _{1}\mathbf {e} _{1}+\dots +\beta _{n}\mathbf {e} _{n}$to scalars$\mathbf {e} ^{i}(x)=\alpha _{i}$and$\mathbf {e} ^{i}(y)=\beta _{i}$.Then also,$x+\lambda y=(\alpha _{1}+\lambda \beta _{1})\mathbf {e} _{1}+\dots +(\alpha _{n}+\lambda \beta _{n})\mathbf {e} _{n}$and$\mathbf {e} ^{i}(x+\lambda y)=\alpha _{i}+\lambda \beta _{i}=\mathbf {e} ^{i}(x)+\lambda \mathbf {e} ^{i}(y)$.Therefore,$\mathbf {e} ^{i}\in V^{*}$for$i=1,2,\dots,n$. Suppose$\lambda _{1}\mathbf {e} ^{1}+\cdots +\lambda _{n}\mathbf {e} ^{n}=0\in V^{*}$.Applying this functional on the basis vectors of$V$successively, lead us to$\lambda _{1}=\lambda _{2}=\dots =\lambda _{n}=0$(The functional applied in$\mathbf {e} _{i}$results in$\lambda _{i}$). Therefore,$\{\mathbf {e} ^{1},\dots,\mathbf {e} ^{n}\}$is linearly independent on$V^{*}$. Lastly, consider$g\in V^{*}$.Then $g(x)=g(\alpha _{1}\mathbf {e} _{1}+\dots +\alpha _{n}\mathbf {e} _{n})=\alpha _{1}g(\mathbf {e} _{1})+\dots +\alpha _{n}g(\mathbf {e} _{n})=\mathbf {e} ^{1}(x)g(\mathbf {e} _{1})+\dots +\mathbf {e} ^{n}(x)g(\mathbf {e} _{n})$ and$\{\mathbf {e} ^{1},\dots,\mathbf {e} ^{n}\}$generates$V^{*}$.Hence, it is a basis of$V^{*}$.

For example, if$V$is$\mathbb {R} ^{2}$,let its basis be chosen as$\{\mathbf {e} _{1}=(1/2,1/2),\mathbf {e} _{2}=(0,1)\}$.The basis vectors are not orthogonal to each other. Then,$\mathbf {e} ^{1}$and$\mathbf {e} ^{2}$areone-forms(functions that map a vector to a scalar) such that$\mathbf {e} ^{1}(\mathbf {e} _{1})=1$,$\mathbf {e} ^{1}(\mathbf {e} _{2})=0$,$\mathbf {e} ^{2}(\mathbf {e} _{1})=0$,and$\mathbf {e} ^{2}(\mathbf {e} _{2})=1$.(Note: The superscript here is the index, not an exponent.) This system of equations can be expressed using matrix notation as

${\begin{bmatrix}e^{11}&e^{12}\\e^{21}&e^{22}\end{bmatrix}}{\begin{bmatrix}e_{11}&e_{21}\\e_{12}&e_{22}\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\end{bmatrix}}.$

Solving for the unknown values in the first matrix shows the dual basis to be$\{\mathbf {e} ^{1}=(2,0),\mathbf {e} ^{2}=(-1,1)\}$.Because$\mathbf {e} ^{1}$and$\mathbf {e} ^{2}$are functionals, they can be rewritten as$\mathbf {e} ^{1}(x,y)=2x$and$\mathbf {e} ^{2}(x,y)=-x+y$.

In general, when$V$is$\mathbb {R} ^{n}$,if$E=[\mathbf {e} _{1}|\cdots |\mathbf {e} _{n}]$is a matrix whose columns are the basis vectors and${\hat {E}}=[\mathbf {e} ^{1}|\cdots |\mathbf {e} ^{n}]$is a matrix whose columns are the dual basis vectors, then

${\hat {E}}^{\textrm {T}}\cdot E=I_{n},$

where$I_{n}$is theidentity matrixof order$n$.The biorthogonality property of these two basis sets allows any point$\mathbf {x} \in V$to be represented as

$\mathbf {x} =\sum _{i}\langle \mathbf {x},\mathbf {e} ^{i}\rangle \mathbf {e} _{i}=\sum _{i}\langle \mathbf {x},\mathbf {e} _{i}\rangle \mathbf {e} ^{i},$

even when the basis vectors are not orthogonal to each other. Strictly speaking, the above statement only makes sense once the inner product$\langle \cdot,\cdot \rangle$and the corresponding duality pairing are introduced, as described below in§ Bilinear products and dual spaces.

In particular,$\mathbb {R} ^{n}$can be interpreted as the space of columns of$n$real numbers,its dual space is typically written as the space ofrowsof$n$real numbers. Such a row acts on$\mathbb {R} ^{n}$as a linear functional by ordinarymatrix multiplication.This is because a functional maps every$n$-vector$x$into a real number$y$.Then, seeing this functional as a matrix$M$,and$x$as an$n\times 1$matrix, and$y$a$1\times 1$matrix (trivially, a real number) respectively, if$Mx=y$then, by dimension reasons,$M$must be a$1\times n$matrix; that is,$M$must be a row vector.

If$V$consists of the space of geometricalvectorsin the plane, then thelevel curvesof an element of$V^{*}$form a family of parallel lines in$V$,because the range is 1-dimensional, so that every point in the range is a multiple of any one nonzero element. So an element of$V^{*}$can be intuitively thought of as a particular family of parallel lines covering the plane. To compute the value of a functional on a given vector, it suffices to determine which of the lines the vector lies on. Informally, this "counts" how many lines the vector crosses. More generally, if$V$is a vector space of any dimension, then thelevel setsof a linear functional in$V^{*}$are parallel hyperplanes in$V$,and the action of a linear functional on a vector can be visualized in terms of these hyperplanes.

Infinite-dimensional case

If$V$is not finite-dimensional but has abasis$\mathbf {e} _{\alpha }$indexed by an infinite set$A$,then the same construction as in the finite-dimensional case yieldslinearly independentelements$\mathbf {e} ^{\alpha }$($\alpha \in A$) of the dual space, but they will not form a basis.

For instance, consider the space$\mathbb {R} ^{\infty }$,whose elements are thosesequencesof real numbers that contain only finitely many non-zero entries, which has a basis indexed by the natural numbers$\mathbb {N}$.For$i\in \mathbb {N}$,$\mathbf {e} _{i}$is the sequence consisting of all zeroes except in the$i$-th position, which is 1. The dual space of$\mathbb {R} ^{\infty }$is (isomorphic to)$\mathbb {R} ^{\mathbb {N} }$,the space ofallsequences of real numbers: each real sequence$(a_{n})$defines a function where the element$(x_{n})$of$\mathbb {R} ^{\infty }$is sent to the number

$\sum _{n}a_{n}x_{n},$

which is a finite sum because there are only finitely many nonzero$x_{n}$.Thedimensionof$\mathbb {R} ^{\infty }$iscountably infinite,whereas$\mathbb {R} ^{\mathbb {N} }$does not have a countable basis.

This observation generalizes to anyinfinite-dimensional vector space$V$over any field$F$:a choice of basis$\{\mathbf {e} _{\alpha }:\alpha \in A\}$identifies$V$with the space$(F^{A})_{0}$of functions$f:A\to F$such that$f_{\alpha }=f(\alpha )$is nonzero for only finitely many$\alpha \in A$,where such a function$f$is identified with the vector

$\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }$

in$V$(the sum is finite by the assumption on$f$,and any$v\in V$may be written uniquely in this way by the definition of the basis).

The dual space of$V$may then be identified with the space$F^{A}$ofallfunctions from$A$to$F$:a linear functional$T$on$V$is uniquely determined by the values$\theta _{\alpha }=T(\mathbf {e} _{\alpha })$it takes on the basis of$V$,and any function$\theta:A\to F$(with$\theta (\alpha )=\theta _{\alpha }$) defines a linear functional$T$on$V$by

$T\left(\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }\right)=\sum _{\alpha \in A}f_{\alpha }T(e_{\alpha })=\sum _{\alpha \in A}f_{\alpha }\theta _{\alpha }.$

Again, the sum is finite because$f_{\alpha }$is nonzero for only finitely many$\alpha$.

The set$(F^{A})_{0}$may be identified (essentially by definition) with thedirect sumof infinitely many copies of$F$(viewed as a 1-dimensional vector space over itself) indexed by$A$,i.e. there are linear isomorphisms

$V\cong (F^{A})_{0}\cong \bigoplus _{\alpha \in A}F.$

On the other hand,$F^{A}$is (again by definition), thedirect productof infinitely many copies of$F$indexed by$A$,and so the identification

$V^{*}\cong \left(\bigoplus _{\alpha \in A}F\right)^{*}\cong \prod _{\alpha \in A}F^{*}\cong \prod _{\alpha \in A}F\cong F^{A}$

is a special case of ageneral resultrelating direct sums (ofmodules) to direct products.

If a vector space is not finite-dimensional, then its (algebraic) dual space isalwaysof larger dimension (as acardinal number) than the original vector space. This is in contrast to the case of the continuous dual space, discussed below, which may beisomorphicto the original vector space even if the latter is infinite-dimensional.

The proof of this inequality between dimensions results from the following.

If$V$is an infinite-dimensional$F$-vector space, the arithmetical properties ofcardinal numbersimplies that

$\mathrm {dim} (V)=|A|<|F|^{|A|}=|V^{\ast }|=\mathrm {max} (|\mathrm {dim} (V^{\ast })|,|F|),$

where cardinalities are denoted asabsolute values.For proving that$\mathrm {dim} (V)<\mathrm {dim} (V^{*}),$it suffices to prove that$|F|\leq |\mathrm {dim} (V^{\ast })|,$which can be done with an argument similar toCantor's diagonal argument.The exact dimension of the dual is given by theErdős–Kaplansky theorem.

Bilinear products and dual spaces

IfVis finite-dimensional, thenVis isomorphic toV^∗.But there is in general nonatural isomorphismbetween these two spaces.Anybilinear form⟨·,·⟩onVgives a mapping ofVinto its dual space via

$v\mapsto \langle v,\cdot \rangle$

where the right hand side is defined as the functional onVtaking eachw∈Vto⟨v,w⟩.In other words, the bilinear form determines a linear mapping

$\Phi _{\langle \cdot,\cdot \rangle }:V\to V^{*}$

defined by

$\left[\Phi _{\langle \cdot,\cdot \rangle }(v),w\right]=\langle v,w\rangle.$

If the bilinear form isnondegenerate,then this is an isomorphism onto a subspace ofV^∗. IfVis finite-dimensional, then this is an isomorphism onto all ofV^∗.Conversely, any isomorphism$\Phi$fromVto a subspace ofV^∗(resp., all ofV^∗ifVis finite dimensional) defines a unique nondegenerate bilinear form$\langle \cdot,\cdot \rangle _{\Phi }$onVby

$\langle v,w\rangle _{\Phi }=(\Phi (v))(w)=[\Phi (v),w].\,$

Thus there is a one-to-one correspondence between isomorphisms ofVto a subspace of (resp., all of)V^∗and nondegenerate bilinear forms onV.

If the vector spaceVis over thecomplexfield, then sometimes it is more natural to considersesquilinear formsinstead of bilinear forms. In that case, a given sesquilinear form⟨·,·⟩determines an isomorphism ofVwith thecomplex conjugateof the dual space

$\Phi _{\langle \cdot,\cdot \rangle }:V\to {\overline {V^{*}}}.$

The conjugate of the dual space${\overline {V^{*}}}$can be identified with the set of all additive complex-valued functionalsf:V→Csuch that

$f(\alpha v)={\overline {\alpha }}f(v).$

Injection into the double-dual

There is anaturalhomomorphism$\Psi$from$V$into the double dual$V^{**}=\{\Phi:V^{*}\to F:\Phi \ \mathrm {linear} \}$,defined by$(\Psi (v))(\varphi )=\varphi (v)$for all$v\in V,\varphi \in V^{*}$.In other words, if$\mathrm {ev} _{v}:V^{*}\to F$is the evaluation map defined by$\varphi \mapsto \varphi (v)$,then$\Psi:V\to V^{**}$is defined as the map$v\mapsto \mathrm {ev} _{v}$.This map$\Psi$is alwaysinjective;and it is always anisomorphismif$V$is finite-dimensional. Indeed, the isomorphism of a finite-dimensional vector space with its double dual is an archetypal example of anatural isomorphism. Infinite-dimensional Hilbert spaces are not isomorphic to their algebraic double duals, but instead to their continuous double duals.

Transpose of a linear map

Main article:Transpose of a linear map

Iff:V→Wis alinear map,then thetranspose(ordual)f^∗:W^∗→V^∗is defined by

$f^{*}(\varphi )=\varphi \circ f\,$

for every$\varphi \in W^{*}$.The resulting functional$f^{*}(\varphi )$in$V^{*}$is called thepullbackof$\varphi$along$f$.

The following identity holds for all$\varphi \in W^{*}$and$v\in V$:

$[f^{*}(\varphi ),\,v]=[\varphi,\,f(v)],$

where the bracket [·,·] on the left is the natural pairing ofVwith its dual space, and that on the right is the natural pairing ofWwith its dual. This identity characterizes the transpose,and is formally similar to the definition of theadjoint.

The assignmentf↦f^∗produces aninjectivelinear map between the space of linear operators fromVtoWand the space of linear operators fromW^∗toV^∗;this homomorphism is anisomorphismif and only ifWis finite-dimensional. IfV=Wthen the space of linear maps is actually analgebraundercomposition of maps,and the assignment is then anantihomomorphismof algebras, meaning that(fg)^∗=g^∗f^∗. In the language ofcategory theory,taking the dual of vector spaces and the transpose of linear maps is therefore acontravariant functorfrom the category of vector spaces overFto itself. It is possible to identify (f^∗)^∗withfusing the natural injection into the double dual.

If the linear mapfis represented by thematrixAwith respect to two bases ofVandW,thenf^∗is represented by thetransposematrixA^Twith respect to the dual bases ofW^∗andV^∗,hence the name. Alternatively, asfis represented byAacting on the left on column vectors,f^∗is represented by the same matrix acting on the right on row vectors. These points of view are related by the canonical inner product onRⁿ,which identifies the space of column vectors with the dual space of row vectors.

Quotient spaces and annihilators

Let$S$be a subset of$V$. Theannihilatorof$S$in$V^{*}$,denoted here$S^{0}$,is the collection of linear functionals$f\in V^{*}$such that$[f,s]=0$for all$s\in S$. That is,$S^{0}$consists of all linear functionals$f:V\to F$such that the restriction to$S$vanishes:$f|_{S}=0$. Within finite dimensional vector spaces, the annihilator is dual to (isomorphic to) theorthogonal complement.

The annihilator of a subset is itself a vector space. The annihilator of the zero vector is the whole dual space:$\{0\}^{0}=V^{*}$,and the annihilator of the whole space is just the zero covector:$V^{0}=\{0\}\subseteq V^{*}$. Furthermore, the assignment of an annihilator to a subset of$V$reverses inclusions, so that if$\{0\}\subseteq S\subseteq T\subseteq V$,then

$\{0\}\subseteq T^{0}\subseteq S^{0}\subseteq V^{*}.$

If$A$and$B$are two subsets of$V$then

$A^{0}+B^{0}\subseteq (A\cap B)^{0}.$

If$(A_{i})_{i\in I}$is any family of subsets of$V$indexed by$i$belonging to some index set$I$,then

$\left(\bigcup _{i\in I}A_{i}\right)^{0}=\bigcap _{i\in I}A_{i}^{0}.$

In particular if$A$and$B$are subspaces of$V$then

$(A+B)^{0}=A^{0}\cap B^{0}$

and

$(A\cap B)^{0}=A^{0}+B^{0}.$

If$V$is finite-dimensional and$W$is avector subspace,then

$W^{00}=W$

after identifying$W$with its image in the second dual space under the double duality isomorphism$V\approx V^{**}$.In particular, forming the annihilator is aGalois connectionon the lattice of subsets of a finite-dimensional vector space.

If$W$is a subspace of$V$then thequotient space$V/W$is a vector space in its own right, and so has a dual. By thefirst isomorphism theorem,a functional$f:V\to F$factors through$V/W$if and only if$W$is in thekernelof$f$.There is thus an isomorphism

$(V/W)^{*}\cong W^{0}.$

As a particular consequence, if$V$is adirect sumof two subspaces$A$and$B$,then$V^{*}$is a direct sum of$A^{0}$and$B^{0}$.

Dimensional analysis

The dual space is analogous to a "negative" -dimensional space. Most simply, since a vector$v\in V$can be paired with a covector$\varphi \in V^{*}$by the natural pairing $\langle x,\varphi \rangle:=\varphi (x)\in F$to obtain a scalar, a covector can "cancel" the dimension of a vector, similar toreducing a fraction.Thus while the direct sum$V\oplus V^{*}$is a⁠$2n$⁠-dimensional space (if⁠$V$⁠is⁠$n$⁠-dimensional),⁠$V^{*}$⁠behaves as an⁠$(-n)$⁠-dimensional space, in the sense that its dimensions can be canceled against the dimensions of⁠$V$⁠.This is formalized bytensor contraction.

This arises in physics viadimensional analysis,where the dual space has inverse units.Under the natural pairing, these units cancel, and the resulting scalar value isdimensionless,as expected. For example, in (continuous)Fourier analysis,or more broadlytime–frequency analysis:given a one-dimensional vector space with aunit of time⁠$t$⁠,the dual space has units offrequency:occurrencesperunit of time (units of⁠$1/t$⁠). For example, if time is measured inseconds,the corresponding dual unit is theinverse second:over the course of 3 seconds, an event that occurs 2 times per second occurs a total of 6 times, corresponding to$3s\cdot 2s^{-1}=6$.Similarly, if the primal space measures length, the dual space measuresinverse length.

Continuous dual space

When dealing withtopological vector spaces,thecontinuouslinear functionals from the space into the base field$\mathbb {F} =\mathbb {C}$(or$\mathbb {R}$) are particularly important. This gives rise to the notion of the "continuous dual space" or "topological dual" which is a linear subspace of the algebraic dual space$V^{*}$,denoted by$V'$. For anyfinite-dimensionalnormed vector space or topological vector space, such asEuclideann-space,the continuous dual and the algebraic dual coincide. This is however false for any infinite-dimensional normed space, as shown by the example ofdiscontinuous linear maps. Nevertheless, in the theory oftopological vector spacesthe terms "continuous dual space" and "topological dual space" are often replaced by "dual space".

For atopological vector space$V$itscontinuous dual space,ortopological dual space,or justdual space(in the sense of the theory of topological vector spaces)$V'$is defined as the space of all continuous linear functionals$\varphi:V\to {\mathbb {F} }$.

Important examples for continuous dual spaces are the space of compactly supportedtest functions${\mathcal {D}}$and its dual${\mathcal {D}}',$the space of arbitrarydistributions(generalized functions); the space of arbitrary test functions${\mathcal {E}}$and its dual${\mathcal {E}}',$the space of compactly supported distributions; and the space of rapidly decreasing test functions${\mathcal {S}},$theSchwartz space,and its dual${\mathcal {S}}',$the space oftempered distributions(slowly growing distributions) in the theory ofgeneralized functions.

Properties

IfXis aHausdorfftopological vector space(TVS), then the continuous dual space ofXis identical to the continuous dual space of thecompletionofX.

Topologies on the dual

Main articles:Polar topologyandDual system

There is a standard construction for introducing a topology on the continuous dual$V'$of a topological vector space$V$.Fix a collection${\mathcal {A}}$ofbounded subsetsof$V$. This gives the topology on$V$of uniform convergence on sets from${\mathcal {A}},$or what is the same thing, the topology generated byseminormsof the form

$\|\varphi \|_{A}=\sup _{x\in A}|\varphi (x)|,$

where$\varphi$is a continuous linear functional on$V$,and$A$runs over the class${\mathcal {A}}.$

This means that a net of functionals$\varphi _{i}$tends to a functional$\varphi$in$V'$if and only if

${\text{ for all }}A\in {\mathcal {A}}\qquad \|\varphi _{i}-\varphi \|_{A}=\sup _{x\in A}|\varphi _{i}(x)-\varphi (x)|{\underset {i\to \infty }{\longrightarrow }}0.$

Usually (but not necessarily) the class${\mathcal {A}}$is supposed to satisfy the following conditions:

• Each point$x$of$V$belongs to some set$A\in {\mathcal {A}}$:

  ${\text{ for all }}x\in V\quad {\text{ there exists some }}A\in {\mathcal {A}}\quad {\text{ such that }}x\in A.$

• Each two sets$A\in {\mathcal {A}}$and$B\in {\mathcal {A}}$are contained in some set$C\in {\mathcal {A}}$:

  ${\text{ for all }}A,B\in {\mathcal {A}}\quad {\text{ there exists some }}C\in {\mathcal {A}}\quad {\text{ such that }}A\cup B\subseteq C.$

• ${\mathcal {A}}$is closed under the operation of multiplication by scalars:

  ${\text{ for all }}A\in {\mathcal {A}}\quad {\text{ and all }}\lambda \in {\mathbb {F} }\quad {\text{ such that }}\lambda \cdot A\in {\mathcal {A}}.$

If these requirements are fulfilled then the corresponding topology on$V'$is Hausdorff and the sets

$U_{A}~=~\left\{\varphi \in V'~:~\quad \|\varphi \|_{A}<1\right\},\qquad {\text{ for }}A\in {\mathcal {A}}$

form its local base.

Here are the three most important special cases.

• Thestrong topologyon$V'$is the topology of uniform convergence onbounded subsetsin$V$(so here${\mathcal {A}}$can be chosen as the class of all bounded subsets in$V$).

If$V$is anormed vector space(for example, aBanach spaceor aHilbert space) then the strong topology on$V'$is normed (in fact a Banach space if the field of scalars is complete), with the norm

$\|\varphi \|=\sup _{\|x\|\leq 1}|\varphi (x)|.$

• Thestereotype topologyon$V'$is the topology of uniform convergence ontotally bounded setsin$V$(so here${\mathcal {A}}$can be chosen as the class of all totally bounded subsets in$V$).
• Theweak topologyon$V'$is the topology of uniform convergence on finite subsets in$V$(so here${\mathcal {A}}$can be chosen as the class of all finite subsets in$V$).

Each of these three choices of topology on$V'$leads to a variant ofreflexivity propertyfor topological vector spaces:

• If$V'$is endowed with thestrong topology,then the corresponding notion of reflexivity is the standard one: the spaces reflexive in this sense are just calledreflexive.
• If$V'$is endowed with the stereotype dual topology, then the corresponding reflexivity is presented in the theory ofstereotype spaces:the spaces reflexive in this sense are calledstereotype.
• If$V'$is endowed with theweak topology,then the corresponding reflexivity is presented in the theory ofdual pairs:the spaces reflexive in this sense are arbitrary (Hausdorff) locally convex spaces with the weak topology.

Examples

Let 1 <p< ∞ be a real number and consider the Banach spaceℓ^pof allsequencesa= (a_n)for which

$\|\mathbf {a} \|_{p}=\left(\sum _{n=0}^{\infty }|a_{n}|^{p}\right)^{\frac {1}{p}}<\infty.$

Define the numberqby1/p+ 1/q= 1.Then the continuous dual ofℓ^pis naturally identified withℓ^q:given an element$\varphi \in (\ell ^{p})'$,the corresponding element ofℓ^qis the sequence$(\varphi (\mathbf {e} _{n}))$where$\mathbf {e} _{n}$denotes the sequence whosen-th term is 1 and all others are zero. Conversely, given an elementa= (a_n) ∈ℓ^q,the corresponding continuous linear functional$\varphi$onℓ^pis defined by

$\varphi (\mathbf {b} )=\sum _{n}a_{n}b_{n}$

for allb= (b_n) ∈ℓ^p(seeHölder's inequality).

In a similar manner, the continuous dual ofℓ¹is naturally identified withℓ^∞(the space of bounded sequences). Furthermore, the continuous duals of the Banach spacesc(consisting of allconvergentsequences, with thesupremum norm) andc₀(the sequences converging to zero) are both naturally identified withℓ¹.

By theRiesz representation theorem,the continuous dual of a Hilbert space is again a Hilbert space which isanti-isomorphicto the original space. This gives rise to thebra–ket notationused by physicists in the mathematical formulation ofquantum mechanics.

By theRiesz–Markov–Kakutani representation theorem,the continuous dual of certain spaces of continuous functions can be described using measures.

Transpose of a continuous linear map

See also:Transpose of a linear mapandDual system § Transposes

IfT:V → Wis a continuous linear map between two topological vector spaces, then the (continuous) transposeT′:W′ → V′is defined by the same formula as before:

$T'(\varphi )=\varphi \circ T,\quad \varphi \in W'.$

The resulting functionalT′(φ)is inV′.The assignmentT → T′produces a linear map between the space of continuous linear maps fromVtoWand the space of linear maps fromW′toV′. WhenTandUare composable continuous linear maps, then

$(U\circ T)'=T'\circ U'.$

WhenVandWare normed spaces, the norm of the transpose inL(W′,V′)is equal to that ofTinL(V,W). Several properties of transposition depend upon theHahn–Banach theorem. For example, the bounded linear mapThas dense range if and only if the transposeT′is injective.

WhenTis acompactlinear map between two Banach spacesVandW,then the transposeT′is compact. This can be proved using theArzelà–Ascoli theorem.

WhenVis a Hilbert space, there is an antilinear isomorphismi_VfromVonto its continuous dualV′. For every bounded linear mapTonV,the transpose and theadjointoperators are linked by

$i_{V}\circ T^{*}=T'\circ i_{V}.$

WhenTis a continuous linear map between two topological vector spacesVandW,then the transposeT′is continuous whenW′andV′are equipped with "compatible" topologies: for example, when forX=VandX=W,both dualsX′have thestrong topologyβ(X′,X)of uniform convergence on bounded sets ofX,or both have the weak-∗ topologyσ(X′,X)of pointwise convergence onX. The transposeT′is continuous fromβ(W′,W)toβ(V′,V),or fromσ(W′,W)toσ(V′,V).

Annihilators

Assume thatWis a closed linear subspace of a normed spaceV,and consider the annihilator ofWinV′,

$W^{\perp }=\{\varphi \in V':W\subseteq \ker \varphi \}.$

Then, the dual of the quotientV / W can be identified withW^⊥,and the dual ofWcan be identified with the quotientV′ / W^⊥. Indeed, letPdenote the canonicalsurjectionfromVonto the quotientV / W ;then, the transposeP′is an isometric isomorphism from(V / W )′intoV′,with range equal toW^⊥. Ifjdenotes the injection map fromWintoV,then the kernel of the transposej′is the annihilator ofW:

$\ker(j')=W^{\perp }$

and it follows from theHahn–Banach theoremthatj′induces an isometric isomorphism V′ / W^⊥→W′.

Further properties

If the dual of a normed spaceVisseparable,then so is the spaceVitself. The converse is not true: for example, the spaceℓ¹is separable, but its dualℓ^∞is not.

Double dual

This is anatural transformationof vector addition from a vector space to its double dual.⟨x₁,x₂⟩denotes theordered pairof two vectors. The addition + sendsx₁andx₂tox₁+x₂.The addition +′ induced by the transformation can be defined as$[\Psi (x_{1})+'\Psi (x_{2})](\varphi )=\varphi (x_{1}+x_{2})=\varphi (x)$for any$\varphi$in the dual space.

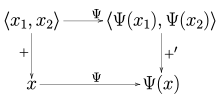
In analogy with the case of the algebraic double dual, there is always a naturally defined continuous linear operatorΨ:V→V′′from a normed spaceVinto its continuous double dualV′′,defined by

$\Psi (x)(\varphi )=\varphi (x),\quad x\in V,\ \varphi \in V'.$

As a consequence of theHahn–Banach theorem,this map is in fact anisometry,meaning‖ Ψ(x) ‖ = ‖x‖for allx∈V. Normed spaces for which the map Ψ is abijectionare calledreflexive.

WhenVis atopological vector spacethen Ψ(x) can still be defined by the same formula, for everyx∈V,however several difficulties arise. First, whenVis notlocally convex,the continuous dual may be equal to { 0 } and the map Ψ trivial. However, ifVisHausdorffand locally convex, the map Ψ is injective fromVto the algebraic dualV′^∗of the continuous dual, again as a consequence of the Hahn–Banach theorem.

Second, even in the locally convex setting, several natural vector space topologies can be defined on the continuous dualV′,so that the continuous double dualV′′is not uniquely defined as a set. Saying that Ψ maps fromVtoV′′,or in other words, that Ψ(x) is continuous onV′for everyx∈V,is a reasonable minimal requirement on the topology ofV′,namely that the evaluation mappings

$\varphi \in V'\mapsto \varphi (x),\quad x\in V,$

be continuous for the chosen topology onV′.Further, there is still a choice of a topology onV′′,and continuity of Ψ depends upon this choice. As a consequence, definingreflexivityin this framework is more involved than in the normed case.

See also

• Covariance and contravariance of vectors
• Dual module
• Dual norm
• Duality (mathematics)
• Duality (projective geometry)
• Pontryagin duality
• Reciprocal lattice– dual space basis, in crystallography

Bibliography

• Axler, Sheldon Jay(2015).Linear Algebra Done Right(3rd ed.).Springer.ISBN978-3-319-11079-0.
• Bourbaki, Nicolas(1989).Elements of mathematics, Algebra I.Springer-Verlag.ISBN3-540-64243-9.
• Bourbaki, Nicolas(2003).Elements of mathematics, Topological vector spaces.Springer-Verlag.
• Halmos, Paul Richard(1974) [1958].Finite-Dimensional Vector Spaces(2nd ed.).Springer.ISBN0-387-90093-4.
• Katznelson, Yitzhak;Katznelson, Yonatan R. (2008).A (Terse) Introduction to Linear Algebra.American Mathematical Society.ISBN978-0-8218-4419-9.
• Lang, Serge(2002),Algebra,Graduate Texts in Mathematics,vol. 211 (Revised third ed.), New York: Springer-Verlag,ISBN978-0-387-95385-4,MR1878556,Zbl0984.00001
• Tu, Loring W.(2011).An Introduction to Manifolds(2nd ed.).Springer.ISBN978-1-4419-7400-6.
• Mac Lane, Saunders;Birkhoff, Garrett(1999).Algebra(3rd ed.). AMS Chelsea Publishing.ISBN0-8218-1646-2..
• Misner, Charles W.;Thorne, Kip S.;Wheeler, John A.(1973).Gravitation.W. H. Freeman.ISBN0-7167-0344-0.
• Narici, Lawrence; Beckenstein, Edward (2011).Topological Vector Spaces.Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press.ISBN978-1584888666.OCLC144216834.
• Rudin, Walter(1973).Functional Analysis.International Series in Pure and Applied Mathematics. Vol. 25 (First ed.). New York, NY:McGraw-Hill Science/Engineering/Math.ISBN9780070542259.
• Rudin, Walter(1991).Functional Analysis.International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY:McGraw-Hill Science/Engineering/Math.ISBN978-0-07-054236-5.OCLC21163277.
• Robertson, A.P.; Robertson, W. (1964).Topological vector spaces.Cambridge University Press.
• Schaefer, Helmut H.(1966).Topological vector spaces.New York: The Macmillan Company.
• Schaefer, Helmut H.;Wolff, Manfred P. (1999).Topological Vector Spaces.GTM.Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer.ISBN978-1-4612-7155-0.OCLC840278135.
• Trèves, François(2006) [1967].Topological Vector Spaces, Distributions and Kernels.Mineola, N.Y.: Dover Publications.ISBN978-0-486-45352-1.OCLC853623322.

External links

• Weisstein, Eric W."Dual Vector Space".MathWorld.