Gamma distribution

Gamma

Probability density function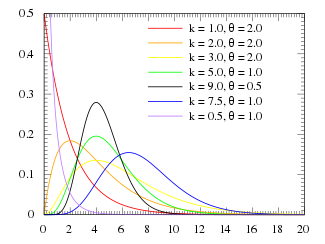
Cumulative distribution function
Parameters	k> 0shape θ> 0scale	α> 0shape β> 0rate
Support	$x\in (0,\infty )$	$x\in (0,\infty )$
PDF	$f(x)={\frac {1}{\Gamma (k)\theta ^{k}}}x^{k-1}e^{-x/\theta }$	$f(x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{\alpha -1}e^{-\beta x}$
CDF	$F(x)={\frac {1}{\Gamma (k)}}\gamma \left(k,{\frac {x}{\theta }}\right)$	$F(x)={\frac {1}{\Gamma (\alpha )}}\gamma (\alpha,\beta x)$
Mean	$k\theta$	${\frac {\alpha }{\beta }}$
Median	No simple closed form	No simple closed form
Mode	$(k-1)\theta {\text{ for }}k\geq 1$,$0{\text{ for }}k<1$	${\frac {\alpha -1}{\beta }}{\text{ for }}\alpha \geq 1{\text{, }}0{\text{ for }}\alpha <1$
Variance	$k\theta ^{2}$	${\frac {\alpha }{\beta ^{2}}}$
Skewness	${\frac {2}{\sqrt {k}}}$	${\frac {2}{\sqrt {\alpha }}}$
Excess kurtosis	${\frac {6}{k}}$	${\frac {6}{\alpha }}$
Entropy	${\begin{aligned}k&+\ln \theta +\ln \Gamma (k)\\&+(1-k)\psi (k)\end{aligned}}$	${\begin{aligned}\alpha &-\ln \beta +\ln \Gamma (\alpha )\\&+(1-\alpha )\psi (\alpha )\end{aligned}}$
MGF	$(1-\theta t)^{-k}{\text{ for }}t<{\frac {1}{\theta }}$	$\left(1-{\frac {t}{\beta }}\right)^{-\alpha }{\text{ for }}t<\beta$
CF	$(1-\theta it)^{-k}$	$\left(1-{\frac {it}{\beta }}\right)^{-\alpha }$
Fisher information	$I(k,\theta )={\begin{pmatrix}\psi ^{(1)}(k)&\theta ^{-1}\\\theta ^{-1}&k\theta ^{-2}\end{pmatrix}}$	$I(\alpha,\beta )={\begin{pmatrix}\psi ^{(1)}(\alpha )&-\beta ^{-1}\\-\beta ^{-1}&\alpha \beta ^{-2}\end{pmatrix}}$
Method of moments	$k={\frac {E[X]^{2}}{V[X]}}\quad \quad$$\theta ={\frac {V[X]}{E[X]}}\quad \quad$	$\alpha ={\frac {E[X]^{2}}{V[X]}}$$\beta ={\frac {E[X]}{V[X]}}$

Inprobability theoryandstatistics,thegamma distributionis a versatile two-parameterfamily of continuousprobability distributions.Theexponential distribution,Erlang distribution,andchi-squared distributionare special cases of the gamma distribution. There are two equivalent parameterizations in common use:

1. With ashape parameterkand ascale parameterθ
2. With a shape parameter$\alpha =k$and an inverse scale parameter⁠$\beta =1/\theta$⁠,called arate parameter.

In each of these forms, both parameters are positive real numbers.

The distribution has important applications in various fields, includingeconometrics,Bayesian statistics,life testing. In econometrics, the (k, θ) parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of anErlang distributionfor integer k values. Bayesian statistics prefer the (α, β) parameterization, utilizing the gamma distribution as aconjugate priorfor several inverse scale parameters, facilitating analytical tractability in posterior distribution computations. The probability density and cumulative distribution functions of the gamma distribution vary based on the chosen parameterization, both offering insights into the behavior of gamma-distributed random variables. The gamma distribution is integral to modeling a range of phenomena due to its flexible shape, which can capture various statistical distributions, including the exponential and chi-squared distributions under specific conditions. Its mathematical properties, such as mean, variance, skewness, and higher moments, provide a toolset for statistical analysis and inference. Practical applications of the distribution span several disciplines, underscoring its importance in theoretical and applied statistics.

The gamma distribution is themaximum entropy probability distribution(both with respect to a uniform base measure and a$1/x$base measure) for a random variableXfor whichE[X] =kθ=α/βis fixed and greater than zero, andE[lnX] =ψ(k) + lnθ=ψ(α) − lnβis fixed (ψis thedigamma function).

Definitions

The parameterization withkandθappears to be more common ineconometricsand other applied fields, where the gamma distribution is frequently used to model waiting times. For instance, inlife testing,the waiting time until death is arandom variablethat is frequently modeled with a gamma distribution. See Hogg and Craigfor an explicit motivation.

The parameterization withαandβis more common inBayesian statistics,where the gamma distribution is used as aconjugate priordistribution for various types of inverse scale (rate) parameters, such as theλof anexponential distributionor aPoisson distribution– or for that matter, theβof the gamma distribution itself. The closely relatedinverse-gamma distributionis used as a conjugate prior for scale parameters, such as thevarianceof anormal distribution.

Ifkis a positiveinteger,then the distribution represents anErlang distribution;i.e., the sum ofkindependentexponentially distributedrandom variables,each of which has a mean ofθ.

Characterization using shapeαand rateβ

The gamma distribution can be parameterized in terms of ashape parameterα=kand an inverse scale parameterβ= 1/θ,called arate parameter.A random variableXthat is gamma-distributed with shapeαand rateβis denoted

$X\sim \Gamma (\alpha,\beta )\equiv \operatorname {Gamma} (\alpha,\beta )$

The corresponding probability density function in the shape-rate parameterization is

${\begin{aligned}f(x;\alpha,\beta )&={\frac {x^{\alpha -1}e^{-\beta x}\beta ^{\alpha }}{\Gamma (\alpha )}}\quad {\text{ for }}x>0\quad \alpha,\beta >0,\\[6pt]\end{aligned}}$

where$\Gamma (\alpha )$is thegamma function. For all positive integers,$\Gamma (\alpha )=(\alpha -1)!$.

Thecumulative distribution functionis the regularized gamma function:

$F(x;\alpha,\beta )=\int _{0}^{x}f(u;\alpha,\beta )\,du={\frac {\gamma (\alpha,\beta x)}{\Gamma (\alpha )}},$

where$\gamma (\alpha,\beta x)$is the lowerincomplete gamma function.

Ifαis a positiveinteger(i.e., the distribution is anErlang distribution), the cumulative distribution function has the following series expansion:

$F(x;\alpha,\beta )=1-\sum _{i=0}^{\alpha -1}{\frac {(\beta x)^{i}}{i!}}e^{-\beta x}=e^{-\beta x}\sum _{i=\alpha }^{\infty }{\frac {(\beta x)^{i}}{i!}}.$

Characterization using shapekand scaleθ

A random variableXthat is gamma-distributed with shapekand scaleθis denoted by

$X\sim \Gamma (k,\theta )\equiv \operatorname {Gamma} (k,\theta )$

Illustration of the gamma PDF for parameter values overkandxwithθset to1, 2, 3, 4, 5,and6.One can see eachθlayer by itself here[2]as well as byk[3]andx.[4].

Theprobability density functionusing the shape-scale parametrization is

$f(x;k,\theta )={\frac {x^{k-1}e^{-x/\theta }}{\theta ^{k}\Gamma (k)}}\quad {\text{ for }}x>0{\text{ and }}k,\theta >0.$

HereΓ(k)is thegamma functionevaluated atk.

Thecumulative distribution functionis the regularized gamma function:

$F(x;k,\theta )=\int _{0}^{x}f(u;k,\theta )\,du={\frac {\gamma \left(k,{\frac {x}{\theta }}\right)}{\Gamma (k)}},$

where$\gamma \left(k,{\frac {x}{\theta }}\right)$is the lowerincomplete gamma function.

It can also be expressed as follows, ifkis a positiveinteger(i.e., the distribution is anErlang distribution):

$F(x;k,\theta )=1-\sum _{i=0}^{k-1}{\frac {1}{i!}}\left({\frac {x}{\theta }}\right)^{i}e^{-x/\theta }=e^{-x/\theta }\sum _{i=k}^{\infty }{\frac {1}{i!}}\left({\frac {x}{\theta }}\right)^{i}.$

Both parametrizations are common because either can be more convenient depending on the situation.

Properties

Mean and variance

The mean of gamma distribution is given by the product of its shape and scale parameters:

$\mu =k\theta =\alpha /\beta$

The variance is:

$\sigma ^{2}=k\theta ^{2}=\alpha /\beta ^{2}$

The square root of the inverse shape parameter gives thecoefficient of variation:

$\sigma /\mu =k^{-0.5}=1/{\sqrt {\alpha }}$

Skewness

Theskewnessof the gamma distribution only depends on its shape parameter,k,and it is equal to$2/{\sqrt {k}}.$

Higher moments

Then-thraw momentis given by:

$\mathrm {E} [X^{n}]=\theta ^{n}{\frac {\Gamma (k+n)}{\Gamma (k)}}=\theta ^{n}\prod _{i=1}^{n}(k+i-1)\;{\text{ for }}n=1,2,\ldots.$

Median approximations and bounds

Bounds and asymptotic approximations to the median of the gamma distribution. The cyan-colored region indicates the large gap between published lower and upper bounds before 2021.

Unlike the mode and the mean, which have readily calculable formulas based on the parameters, the median does not have a closed-form equation. The median for this distribution is the valueνsuch that

${\frac {1}{\Gamma (k)\theta ^{k}}}\int _{0}^{\nu }x^{k-1}e^{-x/\theta }dx={\frac {1}{2}}.$

A rigorous treatment of the problem of determining an asymptotic expansion and bounds for the median of the gamma distribution was handled first by Chen and Rubin, who proved that (for$\theta =1$)

$k-{\frac {1}{3}}<\nu (k)<k,$

where$\mu (k)=k$is the mean and$\nu (k)$is the median of the${\text{Gamma}}(k,1)$distribution.For other values of the scale parameter, the mean scales to$\mu =k\theta$,and the median bounds and approximations would be similarly scaled byθ.

K. P. Choi found the first five terms in aLaurent seriesasymptotic approximation of the median by comparing the median toRamanujan's$\theta$function.Berg and Pedersen found more terms:

$\nu (k)=k-{\frac {1}{3}}+{\frac {8}{405k}}+{\frac {184}{25515k^{2}}}+{\frac {2248}{3444525k^{3}}}-{\frac {19006408}{15345358875k^{4}}}-O\left({\frac {1}{k^{5}}}\right)+\cdots$

Two gamma distribution median asymptotes which were proved in 2023 to be bounds (upper solid red and lower dashed red), of the from$\nu (k)\approx 2^{-1/k}(A+k)$,and an interpolation between them that makes an approximation (dotted red) that is exact at k = 1 and has maximum relative error of about 0.6%. The cyan shaded region is the remaining gap between upper and lower bounds (or conjectured bounds), including these new bounds and the bounds in the previous figure.

Log–log plotof upper (solid) and lower (dashed) bounds to the median of a gamma distribution and the gaps between them. The green, yellow, and cyan regions represent the gap before the Lyon 2021 paper. The green and yellow narrow that gap with the lower bounds that Lyon proved. Lyon's bounds proved in 2023 further narrow the yellow. Mostly within the yellow, closed-form rational-function-interpolated conjectured bounds are plotted along with the numerically calculated median (dotted) value. Tighter interpolated bounds exist but are not plotted, as they would not be resolved at this scale.

Partial sums of these series are good approximations for high enoughk;they are not plotted in the figure, which is focused on the low-kregion that is less well approximated.

Berg and Pedersen also proved many properties of the median, showing that it is a convex function ofk,and that the asymptotic behavior near$k=0$is$\nu (k)\approx e^{-\gamma }2^{-1/k}$(whereγis theEuler–Mascheroni constant), and that for all$k>0$the median is bounded by$k2^{-1/k}<\nu (k)<ke^{-1/3k}$.

A closer linear upper bound, for$k\geq 1$only, was provided in 2021 by Gaunt and Merkle,relying on the Berg and Pedersen result that the slope of$\nu (k)$is everywhere less than 1:

$\nu (k)\leq k-1+\log 2~~$for$k\geq 1$(with equality at$k=1$)

which can be extended to a bound for all$k>0$by taking the max with the chord shown in the figure, since the median was proved convex.

An approximation to the median that is asymptotically accurate at highkand reasonable down to$k=0.5$or a bit lower follows from theWilson–Hilferty transformation:

$\nu (k)=k\left(1-{\frac {1}{9k}}\right)^{3}$

which goes negative for$k<1/9$.

In 2021, Lyon proposed several approximations of the form$\nu (k)\approx 2^{-1/k}(A+Bk)$.He conjectured values ofAandBfor which this approximation is an asymptotically tight upper or lower bound for all$k>0$.In particular, he proposed these closed-form bounds, which he proved in 2023:

$\nu _{L\infty }(k)=2^{-1/k}(\log 2-{\frac {1}{3}}+k)\quad$is a lower bound, asymptotically tight as$k\to \infty$

$\nu _{U}(k)=2^{-1/k}(e^{-\gamma }+k)\quad$is an upper bound, asymptotically tight as$k\to 0$

Lyon also showed (informally in 2021, rigorously in 2023) two other lower bounds that are notclosed-form expressions,including this one involving thegamma function,based on solving the integral expression substituting 1 for$e^{-x}$:

$\nu (k)>\left({\frac {2}{\Gamma (k+1)}}\right)^{-1/k}\quad$(approaching equality as$k\to 0$)

and the tangent line at$k=1$where the derivative was found to be$\nu ^{\prime }(1)\approx 0.9680448$:

$\nu (k)\geq \nu (1)+(k-1)\nu ^{\prime }(1)\quad$(with equality at$k=1$)

$\nu (k)\geq \log 2+(k-1)(\gamma -2\operatorname {Ei} (-\log 2)-\log \log 2)$

where Ei is theexponential integral.

Additionally, he showed that interpolations between bounds could provide excellent approximations or tighter bounds to the median, including an approximation that is exact at$k=1$(where$\nu (1)=\log 2$) and has a maximum relative error less than 0.6%. Interpolated approximations and bounds are all of the form

$\nu (k)\approx {\tilde {g}}(k)\nu _{L\infty }(k)+(1-{\tilde {g}}(k))\nu _{U}(k)$

where${\tilde {g}}$is an interpolating function running monotonically from 0 at lowkto 1 at highk,approximating an ideal, or exact, interpolator$g(k)$:

$g(k)={\frac {\nu _{U}(k)-\nu (k)}{\nu _{U}(k)-\nu _{L\infty }(k)}}$

For the simplest interpolating function considered, a first-order rational function

${\tilde {g}}_{1}(k)={\frac {k}{b_{0}+k}}$

the tightest lower bound has

$b_{0}={\frac {{\frac {8}{405}}+e^{-\gamma }\log 2-{\frac {\log ^{2}2}{2}}}{e^{-\gamma }-\log 2+{\frac {1}{3}}}}-\log 2\approx 0.143472$

and the tightest upper bound has

$b_{0}={\frac {e^{-\gamma }-\log 2+{\frac {1}{3}}}{1-{\frac {e^{-\gamma }\pi ^{2}}{12}}}}\approx 0.374654$

The interpolated bounds are plotted (mostly inside the yellow region) in thelog–log plotshown. Even tighter bounds are available using different interpolating functions, but not usually with closed-form parameters like these.

Summation

IfX_ihas aGamma(k_i,θ)distribution fori= 1, 2,...,N(i.e., all distributions have the same scale parameterθ), then

$\sum _{i=1}^{N}X_{i}\sim \mathrm {Gamma} \left(\sum _{i=1}^{N}k_{i},\theta \right)$

provided allX_iareindependent.

For the cases where theX_iareindependentbut have different scale parameters, see Mathaior Moschopoulos.

The gamma distribution exhibitsinfinite divisibility.

Scaling

If

$X\sim \mathrm {Gamma} (k,\theta ),$

then, for anyc> 0,

$cX\sim \mathrm {Gamma} (k,c\,\theta ),$by moment generating functions,

or equivalently, if

$X\sim \mathrm {Gamma} \left(\alpha,\beta \right)$(shape-rate parameterization)

$cX\sim \mathrm {Gamma} \left(\alpha,{\frac {\beta }{c}}\right),$

Indeed, we know that ifXis anexponential r.v.with rateλ,thencXis an exponential r.v. with rateλ/c;the same thing is valid with Gamma variates (and this can be checked using themoment-generating function,see, e.g.,these notes,10.4-(ii)): multiplication by a positive constantcdivides the rate (or, equivalently, multiplies the scale).

Exponential family

The gamma distribution is a two-parameterexponential familywithnatural parametersk− 1and−1/θ(equivalently,α− 1and−β), andnatural statisticsXandlnX.

If the shape parameterkis held fixed, the resulting one-parameter family of distributions is anatural exponential family.

Logarithmic expectation and variance

One can show that

$\operatorname {E} [\ln X]=\psi (\alpha )-\ln \beta$

or equivalently,

$\operatorname {E} [\ln X]=\psi (k)+\ln \theta$

whereψis thedigamma function.Likewise,

$\operatorname {var} [\ln X]=\psi ^{(1)}(\alpha )=\psi ^{(1)}(k)$

where$\psi ^{(1)}$is thetrigamma function.

This can be derived using theexponential familyformula for themoment generating function of the sufficient statistic,because one of the sufficient statistics of the gamma distribution islnx.

Information entropy

Theinformation entropyis

${\begin{aligned}\operatorname {H} (X)&=\operatorname {E} [-\ln p(X)]\\[4pt]&=\operatorname {E} [-\alpha \ln \beta +\ln \Gamma (\alpha )-(\alpha -1)\ln X+\beta X]\\[4pt]&=\alpha -\ln \beta +\ln \Gamma (\alpha )+(1-\alpha )\psi (\alpha ).\end{aligned}}$

In thek,θparameterization, theinformation entropyis given by

$\operatorname {H} (X)=k+\ln \theta +\ln \Gamma (k)+(1-k)\psi (k).$

Kullback–Leibler divergence

Illustration of the Kullback–Leibler (KL) divergence for two gamma PDFs. Hereβ=β₀+ 1which are set to1, 2, 3, 4, 5,and6.The typical asymmetry for the KL divergence is clearly visible.

TheKullback–Leibler divergence(KL-divergence), ofGamma(α_p,β_p)( "true" distribution) fromGamma(α_q,β_q)( "approximating" distribution) is given by

${\begin{aligned}D_{\mathrm {KL} }(\alpha _{p},\beta _{p};\alpha _{q},\beta _{q})={}&(\alpha _{p}-\alpha _{q})\psi (\alpha _{p})-\log \Gamma (\alpha _{p})+\log \Gamma (\alpha _{q})\\&{}+\alpha _{q}(\log \beta _{p}-\log \beta _{q})+\alpha _{p}{\frac {\beta _{q}-\beta _{p}}{\beta _{p}}}.\end{aligned}}$

Written using thek,θparameterization, the KL-divergence ofGamma(k_p,θ_p)fromGamma(k_q,θ_q)is given by

${\begin{aligned}D_{\mathrm {KL} }(k_{p},\theta _{p};k_{q},\theta _{q})={}&(k_{p}-k_{q})\psi (k_{p})-\log \Gamma (k_{p})+\log \Gamma (k_{q})\\&{}+k_{q}(\log \theta _{q}-\log \theta _{p})+k_{p}{\frac {\theta _{p}-\theta _{q}}{\theta _{q}}}.\end{aligned}}$

Laplace transform

TheLaplace transformof the gamma PDF is

$F(s)=(1+\theta s)^{-k}={\frac {\beta ^{\alpha }}{(s+\beta )^{\alpha }}}.$

Related distributions

General

• Let$X_{1},X_{2},\ldots,X_{n}$be$n$independent and identically distributed random variables following anexponential distributionwith rate parameter λ, then$\sum _{i}X_{i}$~ Gamma(n, λ) where n is the shape parameter andλis the rate, and${\textstyle {\bar {X}}={\frac {1}{n}}\sum _{i}X_{i}\sim \operatorname {Gamma} (n,n*\lambda )}$.
• IfX~ Gamma(1,λ)(in the shape–rate parametrization), thenXhas anexponential distributionwith rate parameterλ.In the shape-scale parametrization,X~ Gamma(1,λ)has an exponential distribution with rate parameter1/λ.
• IfX~ Gamma(ν/2, 2)(in the shape–scale parametrization), thenXis identical toχ²(ν),thechi-squared distributionwithνdegrees of freedom. Conversely, ifQ~χ²(ν)andcis a positive constant, thencQ~ Gamma(ν/2, 2c).
• Ifθ= 1/k,one obtains theSchulz-Zimm distribution,which is most prominently used to model polymer chain lengths.
• Ifkis aninteger,the gamma distribution is anErlang distributionand is the probability distribution of the waiting time until thek-th "arrival" in a one-dimensionalPoisson processwith intensity1/θ.If

$X\sim \Gamma (k\in \mathbf {Z},\theta ),\qquad Y\sim \operatorname {Pois} \left({\frac {x}{\theta }}\right),$

then

$P(X>x)=P(Y<k).$

• IfXhas aMaxwell–Boltzmann distributionwith parametera,then

$X^{2}\sim \Gamma \left({\frac {3}{2}},2a^{2}\right).$

• IfX~ Gamma(k,θ),then${\textstyle \log X}$follows an exponential-gamma (abbreviated exp-gamma) distribution.It is sometimes referred to as the log-gamma distribution.Formulas for its mean and variance are in the section#Logarithmic expectation and variance.
• IfX~ Gamma(k,θ),then${\sqrt {X}}$follows ageneralized gamma distributionwith parametersp= 2,d= 2k,and$a={\sqrt {\theta }}$.
• More generally, ifX~ Gamma(k,θ),then$X^{q}$for$q>0$follows ageneralized gamma distributionwith parametersp= 1/q,d=k/q,and$a=\theta ^{q}$.
• IfX~ Gamma(k,θ)with shapekand scaleθ,then1/X~ Inv-Gamma(k,θ⁻¹)(seeInverse-gamma distributionfor derivation).
• Parametrization 1: If$X_{k}\sim \Gamma (\alpha _{k},\theta _{k})\,$are independent, then${\frac {\alpha _{2}\theta _{2}X_{1}}{\alpha _{1}\theta _{1}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})$,or equivalently,${\frac {X_{1}}{X_{2}}}\sim \beta '\left(\alpha _{1},\alpha _{2},1,{\frac {\theta _{1}}{\theta _{2}}}\right)$
• Parametrization 2: If$X_{k}\sim \Gamma (\alpha _{k},\beta _{k})\,$are independent, then${\frac {\alpha _{2}\beta _{1}X_{1}}{\alpha _{1}\beta _{2}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})$,or equivalently,${\frac {X_{1}}{X_{2}}}\sim \beta '\left(\alpha _{1},\alpha _{2},1,{\frac {\beta _{2}}{\beta _{1}}}\right)$
• IfX~ Gamma(α,θ)andY~ Gamma(β,θ)are independently distributed, thenX/(X+Y)has abeta distributionwith parametersαandβ,andX/(X+Y)is independent ofX+Y,which isGamma(α+β,θ)-distributed.
• IfX_i~ Gamma(α_i,1)are independently distributed, then the vector (X₁/S,...,X_n/S),whereS=X₁+... +X_n,follows aDirichlet distributionwith parametersα₁,...,α_n.
• For largekthe gamma distribution converges tonormal distributionwith meanμ=kθand varianceσ²=kθ².
• The gamma distribution is theconjugate priorfor the precision of thenormal distributionwith knownmean.
• Thematrix gamma distributionand theWishart distributionare multivariate generalizations of the gamma distribution (samples are positive-definite matrices rather than positive real numbers).
• The gamma distribution is a special case of thegeneralized gamma distribution,thegeneralized integer gamma distribution,and thegeneralized inverse Gaussian distribution.
• Among the discrete distributions, thenegative binomial distributionis sometimes considered the discrete analog of the gamma distribution.
• Tweedie distributions– the gamma distribution is a member of the family of Tweedieexponential dispersion models.
• ModifiedHalf-normal distribution– the Gamma distribution is a member of the family ofModified half-normal distribution.The corresponding density is$f(x\mid \alpha,\beta,\gamma )={\frac {2\beta ^{\frac {\alpha }{2}}x^{\alpha -1}\exp(-\beta x^{2}+\gamma x)}{\Psi {\left({\frac {\alpha }{2}},{\frac {\gamma }{\sqrt {\beta }}}\right)}}}$,where$\Psi (\alpha,z)={}_{1}\Psi _{1}\left({\begin{matrix}\left(\alpha,{\frac {1}{2}}\right)\\(1,0)\end{matrix}};z\right)$denotes theFox–Wright Psi function.
• For the shape-scale parameterization$x|\theta \sim \Gamma (k,\theta )$,if the scale parameter$\theta \sim IG(b,1)$where$IG$denotes theInverse-gamma distribution,then the marginal distribution$x\sim \beta '(k,b)$where$\beta '$denotes theBeta prime distribution.

Compound gamma

If the shape parameter of the gamma distribution is known, but the inverse-scale parameter is unknown, then a gamma distribution for the inverse scale forms a conjugate prior. Thecompound distribution,which results from integrating out the inverse scale, has a closed-form solution known as thecompound gamma distribution.

If, instead, the shape parameter is known but the mean is unknown, with the prior of the mean being given by another gamma distribution, then it results inK-distribution.

Weibull and stable count

The gamma distribution$f(x;k)\,(k>1)$can be expressed as the product distribution of aWeibull distributionand a variant form of thestable count distribution. Its shape parameter$k$can be regarded as the inverse of Lévy's stability parameter in the stable count distribution: $$f(x;k)=\displaystyle \int _{0}^{\infty }{\frac {1}{u}}\,W_{k}\left({\frac {x}{u}}\right)\left[ku^{k-1}\,{\mathfrak {N}}_{\frac {1}{k}}\left(u^{k}\right)\right]\,du,$$ where${\mathfrak {N}}_{\alpha }(\nu )$is a standard stable count distribution of shape$\alpha =1/k$,and$W_{k}(x)$is a standard Weibull distribution of shape$k$.

Statistical inference

Parameter estimation

Maximum likelihood estimation

The likelihood function forNiidobservations(x₁,...,x_N)is

$L(k,\theta )=\prod _{i=1}^{N}f(x_{i};k,\theta )$

from which we calculate the log-likelihood function

$\ell (k,\theta )=(k-1)\sum _{i=1}^{N}\ln x_{i}-\sum _{i=1}^{N}{\frac {x_{i}}{\theta }}-Nk\ln \theta -N\ln \Gamma (k)$

Finding the maximum with respect toθby taking the derivative and setting it equal to zero yields themaximum likelihoodestimator of theθparameter, which equals thesample mean${\bar {x}}$divided by the shape parameterk:

${\hat {\theta }}={\frac {1}{kN}}\sum _{i=1}^{N}x_{i}={\frac {\bar {x}}{k}}$

Substituting this into the log-likelihood function gives

$\ell (k)=(k-1)\sum _{i=1}^{N}\ln x_{i}-Nk-Nk\ln \left({\frac {\sum x_{i}}{kN}}\right)-N\ln \Gamma (k)$

We need at least two samples:$N\geq 2$,because for$N=1$,the function$\ell (k)$increases without bounds as$k\to \infty$.For$k>0$,it can be verified that$\ell (k)$is strictlyconcave,by usinginequality properties of the polygamma function.Finding the maximum with respect tokby taking the derivative and setting it equal to zero yields

$\ln k-\psi (k)=\ln \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)-{\frac {1}{N}}\sum _{i=1}^{N}\ln x_{i}=\ln {\bar {x}}-{\overline {\ln x}}$

whereψis thedigamma functionand${\overline {\ln x}}$is the sample mean oflnx.There is no closed-form solution fork.The function is numerically very well behaved, so if a numerical solution is desired, it can be found using, for example,Newton's method.An initial value ofkcan be found either using themethod of moments,or using the approximation

$\ln k-\psi (k)\approx {\frac {1}{2k}}\left(1+{\frac {1}{6k+1}}\right)$

If we let

$s=\ln \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)-{\frac {1}{N}}\sum _{i=1}^{N}\ln x_{i}=\ln {\bar {x}}-{\overline {\ln x}}$

thenkis approximately

$k\approx {\frac {3-s+{\sqrt {(s-3)^{2}+24s}}}{12s}}$

which is within 1.5% of the correct value.An explicit form for the Newton–Raphson update of this initial guess is:

$k\leftarrow k-{\frac {\ln k-\psi (k)-s}{{\frac {1}{k}}-\psi ^{\prime }(k)}}.$

At the maximum-likelihood estimate$({\hat {k}},{\hat {\theta }})$,the expected values forxand$\ln x$agree with the empirical averages:

${\begin{aligned}{\hat {k}}{\hat {\theta }}&={\bar {x}}&&{\text{and}}&\psi ({\hat {k}})+\ln {\hat {\theta }}&={\overline {\ln x}}.\end{aligned}}$

Caveat for small shape parameter

For data,$(x_{1},\ldots,x_{N})$,that is represented in afloating pointformat that underflows to 0 for values smaller than$\varepsilon$,the logarithms that are needed for the maximum-likelihood estimate will cause failure if there are any underflows. If we assume the data was generated by a gamma distribution with cdf$F(x;k,\theta )$,then the probability that there is at least one underflow is:

$P({\text{underflow}})=1-(1-F(\varepsilon;k,\theta ))^{N}$

This probability will approach 1 for smallkand largeN.For example, at$k=10^{-2}$,$N=10^{4}$and$\varepsilon =2.25\times 10^{-308}$,$P({\text{underflow}})\approx 0.9998$.A workaround is to instead have the data in logarithmic format.

In order to test an implementation of a maximum-likelihood estimator that takes logarithmic data as input, it is useful to be able to generate non-underflowing logarithms of random gamma variates, when$k<1$.Following the implementation inscipy.stats.loggamma,this can be done as follows:sample$Y\sim {\text{Gamma}}(k+1,\theta )$and$U\sim {\text{Uniform}}$independently. Then the required logarithmic sample is$Z=\ln(Y)+\ln(U)/k$,so that$\exp(Z)\sim {\text{Gamma}}(k,\theta )$.

Closed-form estimators

There exist consistent closed-form estimators ofkandθthat are derived from the likelihood of thegeneralized gamma distribution.

The estimate for the shapekis

${\hat {k}}={\frac {N\sum _{i=1}^{N}x_{i}}{N\sum _{i=1}^{N}x_{i}\ln x_{i}-\sum _{i=1}^{N}x_{i}\sum _{i=1}^{N}\ln x_{i}}}$

and the estimate for the scaleθis

${\hat {\theta }}={\frac {1}{N^{2}}}\left(N\sum _{i=1}^{N}x_{i}\ln x_{i}-\sum _{i=1}^{N}x_{i}\sum _{i=1}^{N}\ln x_{i}\right)$

Using the sample mean ofx,the sample mean oflnx,and the sample mean of the productx·lnxsimplifies the expressions to:

${\hat {k}}={\bar {x}}/{\hat {\theta }}$

${\hat {\theta }}={\overline {x\ln {x}}}-{\bar {x}}{\overline {\ln {x}}}.$

If the rate parameterization is used, the estimate of${\hat {\beta }}=1/{\hat {\theta }}$.

These estimators are not strictly maximum likelihood estimators, but are instead referred to as mixed type log-moment estimators. They have however similar efficiency as the maximum likelihood estimators.

Although these estimators are consistent, they have a small bias. A bias-corrected variant of the estimator for the scaleθis

${\tilde {\theta }}={\frac {N}{N-1}}{\hat {\theta }}$

A bias correction for the shape parameterkis given as

${\tilde {k}}={\hat {k}}-{\frac {1}{N}}\left(3{\hat {k}}-{\frac {2}{3}}\left({\frac {\hat {k}}{1+{\hat {k}}}}\right)-{\frac {4}{5}}{\frac {\hat {k}}{(1+{\hat {k}})^{2}}}\right)$

Bayesian minimum mean squared error

With knownkand unknownθ,the posterior density function for theta (using the standard scale-invariantpriorforθ) is

$P(\theta \mid k,x_{1},\dots,x_{N})\propto {\frac {1}{\theta }}\prod _{i=1}^{N}f(x_{i};k,\theta )$

Denoting

$y\equiv \sum _{i=1}^{N}x_{i},\qquad P(\theta \mid k,x_{1},\dots,x_{N})=C(x_{i})\theta ^{-Nk-1}e^{-y/\theta }$

Integration with respect toθcan be carried out using a change of variables, revealing that1/θis gamma-distributed with parametersα=Nk,β=y.

$\int _{0}^{\infty }\theta ^{-Nk-1+m}e^{-y/\theta }\,d\theta =\int _{0}^{\infty }x^{Nk-1-m}e^{-xy}\,dx=y^{-(Nk-m)}\Gamma (Nk-m)\!$

The moments can be computed by taking the ratio (mbym= 0)

$\operatorname {E} [x^{m}]={\frac {\Gamma (Nk-m)}{\Gamma (Nk)}}y^{m}$

which shows that the mean ± standard deviation estimate of the posterior distribution forθis

${\frac {y}{Nk-1}}\pm {\sqrt {\frac {y^{2}}{(Nk-1)^{2}(Nk-2)}}}.$

Bayesian inference

Conjugate prior

InBayesian inference,thegamma distributionis theconjugate priorto many likelihood distributions: thePoisson,exponential,normal(with known mean),Pareto,gamma with known shapeσ,inverse gammawith known shape parameter, andGompertzwith known scale parameter.

The gamma distribution'sconjugate prioris:

$p(k,\theta \mid p,q,r,s)={\frac {1}{Z}}{\frac {p^{k-1}e^{-\theta ^{-1}q}}{\Gamma (k)^{r}\theta ^{ks}}},$

whereZis the normalizing constant with no closed-form solution. The posterior distribution can be found by updating the parameters as follows:

${\begin{aligned}p'&=p\prod \nolimits _{i}x_{i},\\q'&=q+\sum \nolimits _{i}x_{i},\\r'&=r+n,\\s'&=s+n,\end{aligned}}$

wherenis the number of observations, andx_iis thei-th observation.

Occurrence and applications

Consider a sequence of events, with the waiting time for each event being an exponential distribution with rateβ.Then the waiting time for then-th event to occur is the gamma distribution with integer shape$\alpha =n$.This construction of the gamma distribution allows it to model a wide variety of phenomena where several sub-events, each taking time with exponential distribution, must happen in sequence for a major event to occur.Examples include the waiting time ofcell-division events,number of compensatory mutations for a given mutation,waiting time until a repair is necessary for a hydraulic system,and so on.

In biophysics, the dwell time between steps of a molecular motor likeATP synthaseis nearly exponential at constant ATP concentration, revealing that each step of the motor takes a single ATP hydrolysis. If there were n ATP hydrolysis events, then it would be a gamma distribution with degree n.

The gamma distribution has been used to model the size ofinsurance claimsand rainfalls.This means that aggregate insurance claims and the amount of rainfall accumulated in a reservoir are modelled by agamma process– much like theexponential distributiongenerates aPoisson process.

The gamma distribution is also used to model errors in multi-levelPoisson regressionmodels because amixtureofPoisson distributionswith gamma-distributed rates has a known closed form distribution, callednegative binomial.

In wireless communication, the gamma distribution is used to model themulti-path fadingof signal power;see alsoRayleigh distributionandRician distribution.

Inoncology,the age distribution ofcancerincidenceoften follows the gamma distribution, wherein the shape and scale parameters predict, respectively, the number ofdriver eventsand the time interval between them.

Inneuroscience,the gamma distribution is often used to describe the distribution ofinter-spike intervals.

Inbacterialgene expression,thecopy numberof aconstitutively expressedprotein often follows the gamma distribution, where the scale and shape parameter are, respectively, the mean number of bursts per cell cycle and the mean number ofprotein moleculesproduced by a single mRNA during its lifetime.

Ingenomics,the gamma distribution was applied inpeak callingstep (i.e., in recognition of signal) inChIP-chipandChIP-seqdata analysis.

In Bayesian statistics, the gamma distribution is widely used as aconjugate prior.It is the conjugate prior for theprecision(i.e. inverse of the variance) of anormal distribution.It is also the conjugate prior for theexponential distribution.

Inphylogenetics,the gamma distribution is the most commonly used approach to model among-sites rate variationwhenmaximum likelihood,Bayesian,ordistance matrix methodsare used to estimate phylogenetic trees. Phylogenetic analyzes that use the gamma distribution to model rate variation estimate a single parameter from the data because they limit consideration to distributions whereα=β.This parameterization means that the mean of this distribution is 1 and the variance is1/α.Maximum likelihood and Bayesian methods typically use a discrete approximation to the continuous gamma distribution.

Random variate generation

Given the scaling property above, it is enough to generate gamma variables withθ= 1,as we can later convert to any value ofβwith a simple division.

Suppose we wish to generate random variables fromGamma(n+δ,1),where n is a non-negative integer and0 <δ< 1.Using the fact that aGamma(1, 1)distribution is the same as anExp(1)distribution, and noting the method ofgenerating exponential variables,we conclude that ifUisuniformly distributedon (0, 1], then−lnUis distributedGamma(1, 1)(i.e.inverse transform sampling). Now, using the "α-addition "property of gamma distribution, we expand this result:

$-\sum _{k=1}^{n}\ln U_{k}\sim \Gamma (n,1)$

whereU_kare all uniformly distributed on (0, 1] andindependent.All that is left now is to generate a variable distributed asGamma(δ,1)for0 <δ< 1and apply the "α-addition "property once more. This is the most difficult part.

Random generation of gamma variates is discussed in detail by Devroye,noting that none are uniformly fast for all shape parameters. For small values of the shape parameter, the algorithms are often not valid.For arbitrary values of the shape parameter, one can apply the Ahrens and Dietermodified acceptance-rejection method Algorithm GD (shapek≥ 1), or transformation methodwhen0 <k< 1.Also see Cheng and Feast Algorithm GKM 3or Marsaglia's squeeze method.

The following is a version of the Ahrens-Dieteracceptance–rejection method:

1. GenerateU,VandWasiiduniform (0, 1] variates.
2. If$U\leq {\frac {e}{e+\delta }}$then$\xi =V^{1/\delta }$and$\eta =W\xi ^{\delta -1}$.Otherwise,$\xi =1-\ln V$and$\eta =We^{-\xi }$.
3. If$\eta >\xi ^{\delta -1}e^{-\xi }$then go to step 1.
4. ξis distributed asΓ(δ,1).

A summary of this is

$\theta \left(\xi -\sum _{i=1}^{\lfloor k\rfloor }\ln U_{i}\right)\sim \Gamma (k,\theta )$

where$\scriptstyle \lfloor k\rfloor$is the integer part ofk,ξis generated via the algorithm above withδ= {k}(the fractional part ofk) and theU_kare all independent.

While the above approach is technically correct, Devroye notes that it is linear in the value ofkand generally is not a good choice. Instead, he recommends using either rejection-based or table-based methods, depending on context.

For example, Marsaglia's simple transformation-rejection method relying on one normal variateXand one uniform variateU:

1. Set$d=a-{\frac {1}{3}}$and$c={\frac {1}{\sqrt {9d}}}$.
2. Set$v=(1+cX)^{3}$.
3. If$v>0$and$\ln U<{\frac {X^{2}}{2}}+d-dv+d\ln v$return$dv$,else go back to step 2.

With$1\leq a=\alpha =k$generates a gamma distributed random number in time that is approximately constant withk.The acceptance rate does depend onk,with an acceptance rate of 0.95, 0.98, and 0.99 for k=1, 2, and 4. Fork< 1,one can use$\gamma _{\alpha }=\gamma _{1+\alpha }U^{1/\alpha }$to boostkto be usable with this method.

InMatlabnumbers can be generated using the function gamrnd(), which uses the k, θ representation.

External links

• "Gamma-distribution",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Weisstein, Eric W."Gamma distribution".MathWorld.
• ModelAssist (2017)Uses of the gamma distribution in risk modeling, including applied examples in ExcelArchived2017-05-09 at theWayback Machine.
• Engineering Statistics Handbook