Gauge theory

For a more accessible and less technical introduction to this topic, seeIntroduction to gauge theory.

This article discusses the physics of gauge theories. For the mathematical field of gauge theory, seeGauge theory (mathematics).

Inphysics,agauge theoryis a type offield theoryin which theLagrangian,and hence the dynamics of the system itself, do not change underlocal transformationsaccording to certain smooth families of operations (Lie groups). Formally, the Lagrangian isinvariantunder these transformations.

The termgaugerefers to any specific mathematical formalism to regulate redundantdegrees of freedomin the Lagrangian of a physical system. The transformations between possible gauges, calledgauge transformations,form a Lie group—referred to as thesymmetry groupor thegauge groupof the theory. Associated with any Lie group is theLie algebraofgroup generators.For each group generator there necessarily arises a corresponding field (usually avector field) called thegauge field.Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (calledgauge invariance). When such a theory isquantized,thequantaof the gauge fields are calledgauge bosons.If the symmetry group is non-commutative, then the gauge theory is referred to asnon-abeliangauge theory,the usual example being theYang–Mills theory.

Many powerful theories in physics are described byLagrangiansthat areinvariantunder some symmetry transformation groups. When they are invariant under a transformation identically performed ateverypointin thespacetimein which the physical processes occur, they are said to have aglobal symmetry.Local symmetry,the cornerstone of gauge theories, is a stronger constraint. In fact, a global symmetry is just a local symmetry whose group's parameters are fixed in spacetime (the same way a constant value can be understood as a function of a certain parameter, the output of which is always the same).

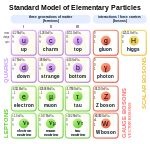
Gauge theories are important as the successful field theories explaining the dynamics ofelementary particles.Quantum electrodynamicsis anabeliangauge theory with the symmetry groupU(1)and has one gauge field, theelectromagnetic four-potential,with thephotonbeing the gauge boson. TheStandard Modelis a non-abelian gauge theory with the symmetry group U(1) ×SU(2)×SU(3)and has a total of twelve gauge bosons: thephoton,threeweak bosonsand eightgluons.

Gauge theories are also important in explaininggravitationin the theory ofgeneral relativity.Its case is somewhat unusual in that the gauge field is a tensor, theLanczos tensor.Theories ofquantum gravity,beginning withgauge gravitation theory,also postulate the existence of a gauge boson known as thegraviton.Gauge symmetries can be viewed as analogues of theprinciple of general covarianceof general relativity in which the coordinate system can be chosen freely under arbitrarydiffeomorphismsof spacetime. Both gauge invariance and diffeomorphism invariance reflect a redundancy in the description of the system. An alternative theory of gravitation,gauge theory gravity,replaces the principle of general covariance with a true gauge principle with new gauge fields.

Historically, these ideas were first stated in the context ofclassical electromagnetismand later ingeneral relativity.However, the modern importance of gauge symmetries appeared first in therelativistic quantum mechanicsofelectrons–quantum electrodynamics,elaborated on below. Today, gauge theories are useful incondensed matter,nuclearandhigh energy physicsamong other subfields.

History

The concept and the name of gauge theory derives from the work ofHermann Weylin 1918.Weyl, in an attempt to generalize the geometrical ideas ofgeneral relativityto includeelectromagnetism,conjectured thatEichinvarianzor invariance under the change ofscale(or "gauge" ) might also be a local symmetry of general relativity. After the development ofquantum mechanics,Weyl,Vladimir FockandFritz Londonreplaced the simple scale factor with acomplexquantity and turned the scale transformation into a change ofphase,which is aU(1)gauge symmetry. This explained theelectromagnetic fieldeffect on thewave functionof achargedquantum mechanicalparticle.Weyl's 1929 paper introduced the modern concept of gauge invariancesubsequently popularized byPauliin his 1941 review.In retrospect,Maxwell's formulation, in 1864–65, ofelectrodynamics( "A Dynamical Theory of the Electromagnetic Field") suggested the possibility of invariance, when he stated that any vector field whose curl vanishes—and can therefore normally be written as agradientof a function—could be added to the vector potential without affecting themagnetic field.Similarly unnoticed,Hilberthad derived theEinstein field equationsby postulating the invariance of theactionunder a general coordinate transformation. The importance of these symmetry invariances remained unnoticed until Weyl's work.

Inspired by Pauli's descriptions of connection between charge conservation and field theory driven by invariance,Chen Ning Yangsought a field theory foratomic nucleibinding based on conservation of nuclearisospin.In 1954, Yang andRobert Millsgeneralized the gauge invariance of electromagnetism, constructing a theory based on the action of the (non-abelian) SU(2) symmetrygroupon theisospindoublet ofprotonsandneutrons.This is similar to the action of theU(1)group on thespinorfieldsofquantum electrodynamics.

TheYang-Mills theorybecame the prototype theory to resolve some of the great confusion inelementary particle physics. This idea later found application in thequantum field theoryof theweak force,and its unification with electromagnetism in theelectroweaktheory. Gauge theories became even more attractive when it was realized that non-abelian gauge theories reproduced a feature calledasymptotic freedom.Asymptotic freedom was believed to be an important characteristic of strong interactions. This motivated searching for a strong force gauge theory. This theory, now known asquantum chromodynamics,is a gauge theory with the action of the SU(3) group on thecolortriplet ofquarks.TheStandard Modelunifies the description of electromagnetism, weak interactions and strong interactions in the language of gauge theory.

In the 1970s,Michael Atiyahbegan studying the mathematics of solutions to the classicalYang–Millsequations. In 1983, Atiyah's studentSimon Donaldsonbuilt on this work to show that thedifferentiableclassification ofsmooth4-manifoldsis very different from their classificationup tohomeomorphism.Michael Freedmanused Donaldson's work to exhibitexoticR⁴s,that is, exoticdifferentiable structuresonEuclidean4-dimensional space. This led to an increasing interest in gauge theory for its own sake, independent of its successes in fundamental physics. In 1994,Edward WittenandNathan Seiberginvented gauge-theoretic techniques based onsupersymmetrythat enabled the calculation of certaintopologicalinvariants(theSeiberg–Witten invariants). These contributions to mathematics from gauge theory have led to a renewed interest in this area.

The importance of gauge theories in physics is exemplified in the tremendous success of the mathematical formalism in providing a unified framework to describe thequantum field theoriesofelectromagnetism,theweak forceand thestrong force.This theory, known as theStandard Model,accurately describes experimental predictions regarding three of the fourfundamental forcesof nature, and is a gauge theory with the gauge groupSU(3) × SU(2) × U(1).Modern theories likestring theory,as well asgeneral relativity,are, in one way or another, gauge theories.

See Jackson and Okunfor early history of gauge and Pickeringfor more about the history of gauge and quantum field theories.

Description

Global and local symmetries

Global symmetry

Inphysics,the mathematical description of any physical situation usually contains excessdegrees of freedom;the same physical situation is equally well described by many equivalent mathematical configurations. For instance, inNewtonian dynamics,if two configurations are related by aGalilean transformation(aninertialchange of reference frame) they represent the same physical situation. These transformations form agroupof "symmetries"of the theory, and a physical situation corresponds not to an individual mathematical configuration but to a class of configurations related to one another by this symmetry group.

This idea can be generalized to include local as well as global symmetries, analogous to much more abstract "changes of coordinates" in a situation where there is no preferred "inertial"coordinate system that covers the entire physical system. A gauge theory is a mathematical model that has symmetries of this kind, together with a set of techniques for making physical predictions consistent with the symmetries of the model.

Example of global symmetry

When a quantity occurring in the mathematical configuration is not just a number but has some geometrical significance, such as a velocity or an axis of rotation, its representation as numbers arranged in a vector or matrix is also changed by a coordinate transformation. For instance, if one description of a pattern of fluid flow states that the fluid velocity in the neighborhood of (x=1,y=0) is 1 m/s in the positivexdirection, then a description of the same situation in which the coordinate system has been rotated clockwise by 90 degrees states that the fluid velocity in the neighborhood of (x= 0,y= −1) is 1 m/s in the negativeydirection. The coordinate transformation has affected both the coordinate system used to identify thelocationof the measurement and the basis in which itsvalueis expressed. As long as this transformation is performed globally (affecting the coordinate basis in the same way at every point), the effect on values that represent therate of changeof some quantity along some path in space and time as it passes through pointPis the same as the effect on values that are truly local toP.

Local symmetry

Use of fiber bundles to describe local symmetries

In order to adequately describe physical situations in more complex theories, it is often necessary to introduce a "coordinate basis" for some of the objects of the theory that do not have this simple relationship to the coordinates used to label points in space and time. (In mathematical terms, the theory involves afiber bundlein which the fiber at each point of the base space consists of possible coordinate bases for use when describing the values of objects at that point.) In order to spell out a mathematical configuration, one must choose a particular coordinate basis at each point (alocal sectionof the fiber bundle) and express the values of the objects of the theory (usually "fields"in the physicist's sense) using this basis. Two such mathematical configurations are equivalent (describe the same physical situation) if they are related by a transformation of this abstract coordinate basis (a change of local section, orgauge transformation).

In most gauge theories, the set of possible transformations of the abstract gauge basis at an individual point in space and time is a finite-dimensional Lie group. The simplest such group isU(1),which appears in the modern formulation ofquantum electrodynamics (QED)via its use ofcomplex numbers.QED is generally regarded as the first, and simplest, physical gauge theory. The set of possible gauge transformations of the entire configuration of a given gauge theory also forms a group, thegauge groupof the theory. An element of the gauge group can be parameterized by a smoothly varying function from the points of spacetime to the (finite-dimensional) Lie group, such that the value of the function and its derivatives at each point represents the action of the gauge transformation on the fiber over that point.

A gauge transformation with constant parameter at every point in space and time is analogous to a rigid rotation of the geometric coordinate system; it represents aglobal symmetryof the gauge representation. As in the case of a rigid rotation, this gauge transformation affects expressions that represent the rate of change along a path of some gauge-dependent quantity in the same way as those that represent a truly local quantity. A gauge transformation whose parameter isnota constant function is referred to as alocal symmetry;its effect on expressions that involve aderivativeis qualitatively different from that on expressions that do not. (This is analogous to a non-inertial change of reference frame, which can produce aCoriolis effect.)

Gauge fields

The "gauge covariant" version of a gauge theory accounts for this effect by introducing agauge field(in mathematical language, anEhresmann connection) and formulating all rates of change in terms of thecovariant derivativewith respect to this connection. The gauge field becomes an essential part of the description of a mathematical configuration. A configuration in which the gauge field can be eliminated by a gauge transformation has the property that itsfield strength(in mathematical language, itscurvature) is zero everywhere; a gauge theory isnotlimited to these configurations. In other words, the distinguishing characteristic of a gauge theory is that the gauge field does not merely compensate for a poor choice of coordinate system; there is generally no gauge transformation that makes the gauge field vanish.

When analyzing thedynamicsof a gauge theory, the gauge field must be treated as a dynamical variable, similar to other objects in the description of a physical situation. In addition to itsinteractionwith other objects via the covariant derivative, the gauge field typically contributesenergyin the form of a "self-energy" term. One can obtain the equations for the gauge theory by:

• starting from a naïveansatzwithout the gauge field (in which the derivatives appear in a "bare" form);
• listing those global symmetries of the theory that can be characterized by a continuous parameter (generally an abstract equivalent of a rotation angle);
• computing the correction terms that result from allowing the symmetry parameter to vary from place to place; and
• reinterpreting these correction terms as couplings to one or more gauge fields, and giving these fields appropriate self-energy terms and dynamical behavior.

This is the sense in which a gauge theory "extends" a global symmetry to a local symmetry, and closely resembles the historical development of the gauge theory of gravity known asgeneral relativity.

Physical experiments

Gauge theories used to model the results of physical experiments engage in:

• limiting the universe of possible configurations to those consistent with the information used to set up the experiment, and then
• computing the probability distribution of the possible outcomes that the experiment is designed to measure.

We cannot express the mathematical descriptions of the "setup information" and the "possible measurement outcomes", or the "boundary conditions" of the experiment, without reference to a particular coordinate system, including a choice of gauge. One assumes an adequate experiment isolated from "external" influence that is itself a gauge-dependent statement. Mishandling gauge dependence calculations in boundary conditions is a frequent source ofanomalies,and approaches to anomaly avoidance classifies gauge theories.

Continuum theories

The two gauge theories mentioned above, continuum electrodynamics and general relativity, are continuum field theories. The techniques of calculation in acontinuum theoryimplicitly assume that:

• given a completely fixed choice of gauge, the boundary conditions of an individual configuration are completely described
• given a completely fixed gauge and a complete set of boundary conditions, the least action determines a unique mathematical configuration and therefore a unique physical situation consistent with these bounds
• fixing the gauge introduces no anomalies in the calculation, due either to gauge dependence in describing partial information about boundary conditions or to incompleteness of the theory.

Determination of the likelihood of possible measurement outcomes proceed by:

• establishing a probability distribution over all physical situations determined by boundary conditions consistent with the setup information
• establishing a probability distribution of measurement outcomes for each possible physical situation
• convolvingthese two probability distributions to get a distribution of possible measurement outcomes consistent with the setup information

These assumptions have enough validity across a wide range of energy scales and experimental conditions to allow these theories to make accurate predictions about almost all of the phenomena encountered in daily life: light, heat, and electricity, eclipses, spaceflight, etc. They fail only at the smallest and largest scales due to omissions in the theories themselves, and when the mathematical techniques themselves break down, most notably in the case ofturbulenceand otherchaoticphenomena.

Quantum field theories

Main article:Quantum field theory

Other than these classical continuum field theories, the most widely known gauge theories arequantum field theories,includingquantum electrodynamicsand theStandard Modelof elementary particle physics. The starting point of a quantum field theory is much like that of its continuum analog: a gauge-covariantaction integralthat characterizes "allowable" physical situations according to theprinciple of least action.However, continuum and quantum theories differ significantly in how they handle the excess degrees of freedom represented by gauge transformations. Continuum theories, and most pedagogical treatments of the simplest quantum field theories, use agauge fixingprescription to reduce the orbit of mathematical configurations that represent a given physical situation to a smaller orbit related by a smaller gauge group (the global symmetry group, or perhaps even the trivial group).

More sophisticated quantum field theories, in particular those that involve a non-abelian gauge group, break the gauge symmetry within the techniques ofperturbation theoryby introducing additional fields (theFaddeev–Popov ghosts) and counterterms motivated byanomaly cancellation,in an approach known asBRST quantization.While these concerns are in one sense highly technical, they are also closely related to the nature of measurement, the limits on knowledge of a physical situation, and the interactions between incompletely specified experimental conditions and incompletely understood physical theory.The mathematical techniques that have been developed in order to make gauge theories tractable have found many other applications, fromsolid-state physicsandcrystallographytolow-dimensional topology.

Classical gauge theory

Classical electromagnetism

Inelectrostatics,one can either discuss the electric field,E,or its correspondingelectric potential,V.Knowledge of one makes it possible to find the other, except that potentials differing by a constant,$V\mapsto V+C$,correspond to the same electric field. This is because the electric field relates tochangesin the potential from one point in space to another, and the constantCwould cancel out when subtracting to find the change in potential. In terms ofvector calculus,the electric field is thegradientof the potential,$\mathbf {E} =-\nabla V$.Generalizing from static electricity to electromagnetism, we have a second potential, thevector potentialA,with

${\begin{aligned}\mathbf {E} &=-\nabla V-{\frac {\partial \mathbf {A} }{\partial t}}\\\mathbf {B} &=\nabla \times \mathbf {A} \end{aligned}}$

The general gauge transformations now become not just$V\mapsto V+C$but

${\begin{aligned}\mathbf {A} &\mapsto \mathbf {A} +\nabla f\\V&\mapsto V-{\frac {\partial f}{\partial t}}\end{aligned}}$

wherefis any twice continuously differentiable function that depends on position and time. The electromagnetic fields remain the same under the gauge transformation.

An example: Scalar O(n) gauge theory

The remainder of this section requires some familiarity withclassicalorquantum field theory,and the use ofLagrangians.

Definitions in this section:gauge group,gauge field,interaction Lagrangian,gauge boson.

The following illustrates how local gauge invariance can be "motivated" heuristically starting from global symmetry properties, and how it leads to an interaction between originally non-interacting fields.

Consider a set of$n$non-interacting realscalar fields,with equal massesm.This system is described by anactionthat is the sum of the (usual) action for each scalar field$\varphi _{i}$

${\mathcal {S}}=\int \,\mathrm {d} ^{4}x\sum _{i=1}^{n}\left[{\frac {1}{2}}\partial _{\mu }\varphi _{i}\partial ^{\mu }\varphi _{i}-{\frac {1}{2}}m^{2}\varphi _{i}^{2}\right]$

The Lagrangian (density) can be compactly written as

$\ {\mathcal {L}}={\frac {1}{2}}(\partial _{\mu }\Phi )^{\mathsf {T}}\partial ^{\mu }\Phi -{\frac {1}{2}}m^{2}\Phi ^{\mathsf {T}}\Phi$

by introducing avectorof fields

$\ \Phi ^{\mathsf {T}}=(\varphi _{1},\varphi _{2},\ldots,\varphi _{n})$

The term$\partial _{\mu }\Phi$is thepartial derivativeof$\Phi$along dimension$\mu$.

It is now transparent that the Lagrangian is invariant under the transformation

$\ \Phi \mapsto \Phi '=G\Phi$

wheneverGis aconstantmatrixbelonging to then-by-northogonal groupO(n). This is seen to preserve the Lagrangian, since the derivative of$\Phi '$transforms identically to$\Phi$and both quantities appear insidedot productsin the Lagrangian (orthogonal transformations preserve the dot product).

$\ (\partial _{\mu }\Phi )\mapsto (\partial _{\mu }\Phi )'=G\partial _{\mu }\Phi$

This characterizes theglobalsymmetry of this particular Lagrangian, and the symmetry group is often called thegauge group;the mathematical term isstructure group,especially in the theory ofG-structures.Incidentally,Noether's theoremimplies that invariance under this group of transformations leads to the conservation of thecurrents

$\ J_{\mu }^{a}=i\partial _{\mu }\Phi ^{\mathsf {T}}T^{a}\Phi$

where theT^amatrices aregeneratorsof the SO(n) group. There is one conserved current for every generator.

Now, demanding that this Lagrangian should havelocalO(n)-invariance requires that theGmatrices (which were earlier constant) should be allowed to become functions of thespacetimecoordinatesx.

In this case, theGmatrices do not "pass through" the derivatives, whenG=G(x),

$\ \partial _{\mu }(G\Phi )\neq G(\partial _{\mu }\Phi )$

The failure of the derivative to commute with "G" introduces an additional term (in keeping with the product rule), which spoils the invariance of the Lagrangian. In order to rectify this we define a new derivative operator such that the derivative of$\Phi '$again transforms identically with$\Phi$

$\ (D_{\mu }\Phi )'=GD_{\mu }\Phi$

This new "derivative" is called a(gauge) covariant derivativeand takes the form

$\ D_{\mu }=\partial _{\mu }-igA_{\mu }$

wheregis called the coupling constant; a quantity defining the strength of an interaction. After a simple calculation we can see that thegauge fieldA(x) must transform as follows

$\ A'_{\mu }=GA_{\mu }G^{-1}-{\frac {i}{g}}(\partial _{\mu }G)G^{-1}$

The gauge field is an element of the Lie algebra, and can therefore be expanded as

$\ A_{\mu }=\sum _{a}A_{\mu }^{a}T^{a}$

There are therefore as many gauge fields as there are generators of the Lie algebra.

Finally, we now have alocally gauge invariantLagrangian

$\ {\mathcal {L}}_{\mathrm {loc} }={\frac {1}{2}}(D_{\mu }\Phi )^{\mathsf {T}}D^{\mu }\Phi -{\frac {1}{2}}m^{2}\Phi ^{\mathsf {T}}\Phi$

Pauli uses the termgauge transformation of the first typeto mean the transformation of$\Phi$,while the compensating transformation in$A$is called agauge transformation of the second type.

Feynman diagramof scalar bosons interacting via a gauge boson

The difference between this Lagrangian and the originalglobally gauge-invariantLagrangian is seen to be theinteraction Lagrangian

$\ {\mathcal {L}}_{\mathrm {int} }=i{\frac {g}{2}}\Phi ^{\mathsf {T}}A_{\mu }^{\mathsf {T}}\partial ^{\mu }\Phi +i{\frac {g}{2}}(\partial _{\mu }\Phi )^{\mathsf {T}}A^{\mu }\Phi -{\frac {g^{2}}{2}}(A_{\mu }\Phi )^{\mathsf {T}}A^{\mu }\Phi$

This term introducesinteractionsbetween thenscalar fields just as a consequence of the demand for local gauge invariance. However, to make this interaction physical and not completely arbitrary, the mediatorA(x) needs to propagate in space. That is dealt with in the next section by adding yet another term,${\mathcal {L}}_{\mathrm {gf} }$,to the Lagrangian. In thequantizedversion of the obtainedclassical field theory,thequantaof the gauge fieldA(x) are calledgauge bosons.The interpretation of the interaction Lagrangian in quantum field theory is ofscalarbosonsinteracting by the exchange of these gauge bosons.

The Yang–Mills Lagrangian for the gauge field

Main article:Yang–Mills theory

The picture of a classical gauge theory developed in the previous section is almost complete, except for the fact that to define the covariant derivativesD,one needs to know the value of the gauge field$A(x)$at all spacetime points. Instead of manually specifying the values of this field, it can be given as the solution to a field equation. Further requiring that the Lagrangian that generates this field equation is locally gauge invariant as well, one possible form for the gauge field Lagrangian is

${\mathcal {L}}_{\text{gf}}=-{\frac {1}{2}}\operatorname {tr} \left(F^{\mu \nu }F_{\mu \nu }\right)=-{\frac {1}{4}}F^{a\mu \nu }F_{\mu \nu }^{a}$

where the$F_{\mu \nu }^{a}$are obtained from potentials$A_{\mu }^{a}$,being the components of$A(x)$,by

$F_{\mu \nu }^{a}=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}+g\sum _{b,c}f^{abc}A_{\mu }^{b}A_{\nu }^{c}$

and the$f^{abc}$are thestructure constantsof the Lie algebra of the generators of the gauge group. This formulation of the Lagrangian is called aYang–Mills action.Other gauge invariant actions also exist (e.g.,nonlinear electrodynamics,Born–Infeld action,Chern–Simons model,theta term,etc.).

In this Lagrangian term there is no field whose transformation counterweighs the one of$A$.Invariance of this term under gauge transformations is a particular case ofa prioriclassical (geometrical) symmetry. This symmetry must be restricted in order to perform quantization, the procedure being denominatedgauge fixing,but even after restriction, gauge transformations may be possible.

The complete Lagrangian for the gauge theory is now

${\mathcal {L}}={\mathcal {L}}_{\text{loc}}+{\mathcal {L}}_{\text{gf}}={\mathcal {L}}_{\text{global}}+{\mathcal {L}}_{\text{int}}+{\mathcal {L}}_{\text{gf}}$

An example: Electrodynamics

As a simple application of the formalism developed in the previous sections, consider the case ofelectrodynamics,with only theelectronfield. The bare-bones action that generates the electron field'sDirac equationis

${\mathcal {S}}=\int {\bar {\psi }}\left(i\hbar c\,\gamma ^{\mu }\partial _{\mu }-mc^{2}\right)\psi \,\mathrm {d} ^{4}x$

The global symmetry for this system is

$\psi \mapsto e^{i\theta }\psi$

The gauge group here isU(1),just rotations of thephase angleof the field, with the particular rotation determined by the constantθ.

"Localising" this symmetry implies the replacement ofθbyθ(x).An appropriate covariant derivative is then

$D_{\mu }=\partial _{\mu }-i{\frac {e}{\hbar }}A_{\mu }$

Identifying the "charge"e(not to be confused with the mathematical constantein the symmetry description) with the usualelectric charge(this is the origin of the usage of the term in gauge theories), and the gauge fieldA(x)with the four-vector potentialof theelectromagnetic fieldresults in an interaction Lagrangian

${\mathcal {L}}_{\text{int}}={\frac {e}{\hbar }}{\bar {\psi }}(x)\gamma ^{\mu }\psi (x)A_{\mu }(x)=J^{\mu }(x)A_{\mu }(x)$

where$J^{\mu }(x)={\frac {e}{\hbar }}{\bar {\psi }}(x)\gamma ^{\mu }\psi (x)$is the electric currentfour vectorin theDirac field.Thegauge principleis therefore seen to naturally introduce the so-calledminimal couplingof the electromagnetic field to the electron field.

Adding a Lagrangian for the gauge field$A_{\mu }(x)$in terms of thefield strength tensorexactly as in electrodynamics, one obtains the Lagrangian used as the starting point inquantum electrodynamics.

${\mathcal {L}}_{\text{QED}}={\bar {\psi }}\left(i\hbar c\,\gamma ^{\mu }D_{\mu }-mc^{2}\right)\psi -{\frac {1}{4\mu _{0}}}F_{\mu \nu }F^{\mu \nu }$

See also:Dirac equation,Maxwell's equations,andQuantum electrodynamics

Mathematical formalism

See also:Gauge theory (mathematics)

Gauge theories are usually discussed in the language ofdifferential geometry.Mathematically, agaugeis just a choice of a (local)sectionof someprincipal bundle.Agauge transformationis just a transformation between two such sections.

Although gauge theory is dominated by the study ofconnections(primarily because it's mainly studied byhigh-energy physicists), the idea of a connection is not central to gauge theory in general. In fact, a result in general gauge theory shows thataffine representations(i.e., affinemodules) of the gauge transformations can be classified as sections of ajet bundlesatisfying certain properties. There are representations that transform covariantly pointwise (called by physicists gauge transformations of the first kind), representations that transform as aconnection form(called by physicists gauge transformations of the second kind, an affine representation)—and other more general representations, such as the B field inBF theory.There are more generalnonlinear representations(realizations), but these are extremely complicated. Still,nonlinear sigma modelstransform nonlinearly, so there are applications.

If there is aprincipal bundlePwhosebase spaceisspaceorspacetimeandstructure groupis a Lie group, then the sections ofPform aprincipal homogeneous spaceof the group of gauge transformations.

Connections(gauge connection) define this principal bundle, yielding acovariant derivative∇ in eachassociated vector bundle.If a local frame is chosen (a local basis of sections), then this covariant derivative is represented by theconnection formA,a Lie algebra-valued1-form,which is called thegauge potentialinphysics.This is evidently not an intrinsic but a frame-dependent quantity. Thecurvature formF,a Lie algebra-valued2-formthat is an intrinsic quantity, is constructed from a connection form by

$\mathbf {F} =\mathrm {d} \mathbf {A} +\mathbf {A} \wedge \mathbf {A}$

where d stands for theexterior derivativeand$\wedge$stands for thewedge product.($\mathbf {A}$is an element of the vector space spanned by the generators$T^{a}$,and so the components of$\mathbf {A}$do not commute with one another. Hence the wedge product$\mathbf {A} \wedge \mathbf {A}$does not vanish.)

Infinitesimal gauge transformations form a Lie algebra, which is characterized by a smooth Lie-algebra-valuedscalar,ε. Under such aninfinitesimalgauge transformation,

$\delta _{\varepsilon }\mathbf {A} =[\varepsilon,\mathbf {A} ]-\mathrm {d} \varepsilon$

where$[\cdot,\cdot ]$is the Lie bracket.

One nice thing is that if$\delta _{\varepsilon }X=\varepsilon X$,then$\delta _{\varepsilon }DX=\varepsilon DX$where D is the covariant derivative

$DX\ {\stackrel {\mathrm {def} }{=}}\ \mathrm {d} X+\mathbf {A} X$

Also,$\delta _{\varepsilon }\mathbf {F} =[\varepsilon,\mathbf {F} ]$,which means$\mathbf {F}$transforms covariantly.

Not all gauge transformations can be generated byinfinitesimalgauge transformations in general. An example is when thebase manifoldis acompactmanifoldwithoutboundarysuch that thehomotopyclass of mappings from thatmanifoldto the Lie group is nontrivial. Seeinstantonfor an example.

TheYang–Mills actionis now given by

${\frac {1}{4g^{2}}}\int \operatorname {Tr} [*F\wedge F]$

where * stands for theHodge dualand the integral is defined as indifferential geometry.

A quantity which isgauge-invariant(i.e.,invariantunder gauge transformations) is theWilson loop,which is defined over any closed path, γ, as follows:

$\chi ^{(\rho )}\left({\mathcal {P}}\left\{e^{\int _{\gamma }A}\right\}\right)$

where χ is thecharacterof a complexrepresentationρ and${\mathcal {P}}$represents the path-ordered operator.

The formalism of gauge theory carries over to a general setting. For example, it is sufficient to ask that avector bundlehave ametric connection;when one does so, one finds that the metric connection satisfies the Yang–Mills equations of motion.

Quantization of gauge theories

Gauge theories may be quantized by specialization of methods which are applicable to anyquantum field theory.However, because of the subtleties imposed by the gauge constraints (see section on Mathematical formalism, above) there are many technical problems to be solved which do not arise in other field theories. At the same time, the richer structure of gauge theories allows simplification of some computations: for exampleWard identitiesconnect differentrenormalizationconstants.

Methods and aims

The first gauge theory quantized wasquantum electrodynamics(QED). The first methods developed for this involved gauge fixing and then applyingcanonical quantization.TheGupta–Bleulermethod was also developed to handle this problem. Non-abelian gauge theories are now handled by a variety of means. Methods for quantization are covered in the article onquantization.

The main point to quantization is to be able to computequantum amplitudesfor various processes allowed by the theory. Technically, they reduce to the computations of certaincorrelation functionsin thevacuum state.This involves arenormalizationof the theory.

When therunning couplingof the theory is small enough, then all required quantities may be computed inperturbation theory.Quantization schemes intended to simplify such computations (such ascanonical quantization) may be calledperturbative quantization schemes.At present some of these methods lead to the most precise experimental tests of gauge theories.

However, in most gauge theories, there are many interesting questions which are non-perturbative. Quantization schemes suited to these problems (such aslattice gauge theory) may be callednon-perturbative quantization schemes.Precise computations in such schemes often requiresupercomputing,and are therefore less well-developed currently than other schemes.

Anomalies

Some of the symmetries of the classical theory are then seen not to hold in the quantum theory; a phenomenon called ananomaly.Among the most well known are:

• Thescale anomaly,which gives rise to arunning coupling constant.In QED this gives rise to the phenomenon of theLandau pole.Inquantum chromodynamics(QCD) this leads toasymptotic freedom.
• Thechiral anomalyin either chiral or vector field theories with fermions. This has close connection withtopologythrough the notion ofinstantons.In QCD this anomaly causes the decay of apionto twophotons.
• Thegauge anomaly,which must cancel in any consistent physical theory. In theelectroweak theorythis cancellation requires an equal number ofquarksandleptons.

Pure gauge

A pure gauge is the set of field configurations obtained by agauge transformationon the null-field configuration, i.e., a gauge transform of zero. So it is a particular "gauge orbit" in the field configuration's space.

Thus, in the abelian case, where$A_{\mu }(x)\rightarrow A'_{\mu }(x)=A_{\mu }(x)+\partial _{\mu }f(x)$,the pure gauge is just the set of field configurations$A'_{\mu }(x)=\partial _{\mu }f(x)$for allf(x).

See also

• Gauge principle
• Aharonov–Bohm effect
• Coulomb gauge
• Electroweak theory
• Gauge covariant derivative
• Gauge fixing
• Gauge gravitation theory
• Gauge group (mathematics)
• Kaluza–Klein theory
• Lorenz gauge
• Quantum chromodynamics
• Gluon field
• Gluon field strength tensor
• Quantum electrodynamics
• Electromagnetic four-potential
• Electromagnetic tensor
• Quantum field theory
• Standard Model
• Standard Model (mathematical formulation)
• Symmetry breaking
• Symmetry in physics
• Charge (physics)
• Symmetry in quantum mechanics
• Fock symmetry
• Ward identities
• Yang–Mills theory
• Yang–Mills existence and mass gap
• 1964 PRL symmetry breaking papers
• Gauge theory (mathematics)

Bibliography

General readers

• Schumm, Bruce (2004)Deep Down Things.Johns Hopkins University Press. Esp. chpt. 8. A serious attempt by a physicist to explain gauge theory and theStandard Modelwith little formal mathematics.

Texts

• Greiner, Walter; Müller, Berndt (2000).Gauge Theory of Weak Interactions.Springer.ISBN3-540-67672-4.
• Cheng, T.-P.;Li, L.-F.(1983).Gauge Theory of Elementary Particle Physics.Oxford University Press.ISBN0-19-851961-3.
• Frampton, P.(2008).Gauge Field Theories(3rd ed.).Wiley-VCH.
• Kane, G.L. (1987).Modern Elementary Particle Physics.Perseus Books.ISBN0-201-11749-5.

Articles

• Becchi, C. (1997). "Introduction to Gauge Theories".arXiv:hep-ph/9705211.
• Gross, D.(1992)."Gauge theory – Past, Present and Future".Retrieved2009-04-23.
• Jackson, J.D.(2002). "From Lorenz to Coulomb and other explicit gauge transformations".Am. J. Phys.70(9): 917–928.arXiv:physics/0204034.Bibcode:2002AmJPh..70..917J.doi:10.1119/1.1491265.S2CID119652556.
• Svetlichny, George (1999). "Preparation for Gauge Theory".arXiv:math-ph/9902027.

External links

• "Gauge transformation",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Yang–Mills equations on DispersiveWiki
• Gauge theories on Scholarpedia