Geometric algebra

For the general algebraic structure, seeClifford algebra.For other uses, seeGeometric algebra (disambiguation).

Not to be confused withAlgebraic geometry.

Inmathematics,ageometric algebra(also known as aClifford algebra) is an extension ofelementary algebrato work with geometrical objects such asvectors.Geometric algebra is built out of two fundamental operations, addition and the geometric product. Multiplication of vectors results in higher-dimensional objects calledmultivectors.Compared to other formalisms for manipulating geometric objects, geometric algebra is noteworthy for supporting vector division (though generally not for all elements) and addition of objects of different dimensions.

The geometric product was first briefly mentioned byHermann Grassmann,who was chiefly interested in developing the closely relatedexterior algebra.In 1878,William Kingdon Cliffordgreatly expanded on Grassmann's work to form what are now usually called Clifford algebras in his honor (although Clifford himself chose to call them "geometric algebras" ). Clifford defined the Clifford algebra and its product as a unification of theGrassmann algebraand Hamilton'squaternion algebra.Adding thedualof the Grassmann exterior product (the "meet" ) allows the use of theGrassmann–Cayley algebra,and aconformal versionof the latter together with a conformal Clifford algebra yields aconformal geometric algebra(CGA) providing a framework forclassical geometries.In practice, these and several derived operations allow a correspondence of elements,subspacesand operations of the algebra with geometric interpretations. For several decades, geometric algebras went somewhat ignored, greatly eclipsed by thevector calculusthen newly developed to describe electromagnetism. The term "geometric algebra" was repopularized in the 1960s byDavid Hestenes,who advocated its importance to relativistic physics.

The scalars and vectors have their usual interpretation and make up distinct subspaces of a geometric algebra.Bivectorsprovide a more natural representation of thepseudovectorquantities of 3D vector calculus that are derived as across product,such as oriented area, oriented angle of rotation, torque, angular momentum and themagnetic field.Atrivectorcan represent an oriented volume, and so on. An element called ablademay be used to represent a subspace andorthogonal projectionsonto that subspace. Rotations and reflections are represented as elements. Unlike a vector algebra, a geometric algebra naturally accommodates any number of dimensions and any quadratic form such as inrelativity.

Examples of geometric algebras applied in physics include thespacetime algebra(and the less commonalgebra of physical space) and theconformal geometric algebra.Geometric calculus,an extension of GA that incorporatesdifferentiationandintegration,can be used to formulate other theories such ascomplex analysisanddifferential geometry,e.g. by using the Clifford algebra instead ofdifferential forms.Geometric algebra has been advocated, most notably byDavid HestenesandChris Doran,as the preferred mathematical framework forphysics.Proponents claim that it provides compact and intuitive descriptions in many areas includingclassicalandquantum mechanics,electromagnetic theory,andrelativity.GA has also found use as a computational tool incomputer graphicsandrobotics.

Definition and notation

There are a number of different ways to define a geometric algebra. Hestenes's original approach was axiomatic,"full of geometric significance" and equivalent to the universalClifford algebra. Given a finite-dimensional vector space⁠$V$⁠over afield⁠$F$⁠with a symmetric bilinear form (theinner product,e.g., the Euclidean orLorentzian metric)⁠$g:V\times V\to F$⁠,thegeometric algebraof thequadratic space⁠$(V,g)$⁠is theClifford algebra⁠$\operatorname {Cl} (V,g)$⁠,an element of which is called a multivector. The Clifford algebra is commonly defined as aquotient algebraof thetensor algebra,though this definition is abstract, so the following definition is presented without requiringabstract algebra.

Definition

A unital associative algebra⁠$\operatorname {Cl} (V,g)$⁠with anondegeneratesymmetric bilinear form⁠$g:V\times V\to F$⁠is the Clifford algebra of the quadratic space⁠$(V,g)$⁠if

• it contains⁠$F$⁠and⁠$V$⁠as distinct subspaces
• ⁠$a^{2}=g(a,a)1$⁠for⁠$a\in V$⁠
• ⁠$V$⁠generates⁠$\operatorname {Cl} (V,g)$⁠as an algebra
• ⁠$\operatorname {Cl} (V,g)$⁠is not generated by any proper subspace of⁠$V$⁠.

To cover degenerate symmetric bilinear forms, the last condition must be modified.It can be shown that these conditions uniquely characterize the geometric product.

For the remainder of this article, only therealcase,⁠$F=\mathbb {R}$⁠,will be considered. The notation⁠${\mathcal {G}}(p,q)$⁠(respectively⁠${\mathcal {G}}(p,q,r)$⁠) will be used to denote a geometric algebra for which the bilinear form⁠$g$⁠has thesignature⁠$(p,q)$⁠(respectively⁠$(p,q,r)$⁠).

The product in the algebra is called thegeometric product,and the product in the contained exterior algebra is called theexterior product(frequently called thewedge productor theouter product). It is standard to denote these respectively by juxtaposition (i.e., suppressing any explicit multiplication symbol) and the symbol⁠$\wedge$⁠.

The above definition of the geometric algebra is still somewhat abstract, so we summarize the properties of the geometric product here. For multivectors⁠$A,B,C\in {\mathcal {G}}(p,q)$⁠:

• ⁠$AB\in {\mathcal {G}}(p,q)$⁠(closure)
• ⁠$1A=A1=A$⁠,where⁠$1$⁠is the identity element (existence of anidentity element)
• ⁠$A(BC)=(AB)C$⁠(associativity)
• ⁠$A(B+C)=AB+AC$⁠and⁠$(B+C)A=BA+CA$⁠(distributivity)
• ⁠$a^{2}=g(a,a)1$⁠for⁠$a\in V$⁠.

The exterior product has the same properties, except that the last property above is replaced by⁠$a\wedge a=0$⁠for⁠$a\in V$⁠.

Note that in the last property above, the real number⁠$g(a,a)$⁠need not be nonnegative if⁠$g$⁠is not positive-definite. An important property of the geometric product is the existence of elements that have a multiplicative inverse. For a vector⁠$a$⁠,if$a^{2}\neq 0$then$a^{-1}$exists and is equal to⁠$g(a,a)^{-1}a$⁠.A nonzero element of the algebra does not necessarily have a multiplicative inverse. For example, if$u$is a vector in$V$such that⁠$u^{2}=1$⁠,the element$\textstyle {\frac {1}{2}}(1+u)$is both a nontrivialidempotent elementand a nonzerozero divisor,and thus has no inverse.

It is usual to identify$\mathbb {R}$and$V$with their images under the naturalembeddings$\mathbb {R} \to {\mathcal {G}}(p,q)$and⁠$V\to {\mathcal {G}}(p,q)$⁠.In this article, this identification is assumed. Throughout, the termsscalarandvectorrefer to elements of$\mathbb {R}$and$V$respectively (and of their images under this embedding).

Geometric product

See also:Symmetric bilinear formandExterior algebra

Given two vectors$a$and⁠$b$⁠,if the geometric product$ab$isanticommutative; they are perpendicular (top) because⁠$a\cdot b=0$⁠,if it is commutative; they are parallel (bottom) because⁠$a\wedge b=0$⁠.

Orientation defined by an ordered set of vectors.

Reversed orientation corresponds to negating the exterior product.

Geometric interpretation of grade-$n$elements in a real exterior algebra for$n=0$(signed point),$1$(directed line segment, or vector),$2$(oriented plane element),$3$(oriented volume). The exterior product of$n$vectors can be visualized as any⁠$n$⁠-dimensional shape (e.g.⁠$n$⁠-parallelotope,⁠$n$⁠-ellipsoid); with magnitude (hypervolume), andorientationdefined by that on its⁠$(n-1)$⁠-dimensional boundary and on which side the interior is.

For vectors⁠$a$⁠and⁠$b$⁠,we may write the geometric product of any two vectors⁠$a$⁠and⁠$b$⁠as the sum of a symmetric product and an antisymmetric product:

$ab={\frac {1}{2}}(ab+ba)+{\frac {1}{2}}(ab-ba).$

Thus we can define theinner productof vectors as

$a\cdot b:=g(a,b),$

so that the symmetric product can be written as

${\frac {1}{2}}(ab+ba)={\frac {1}{2}}\left((a+b)^{2}-a^{2}-b^{2}\right)=a\cdot b.$

Conversely,⁠$g$⁠is completely determined by the algebra. The antisymmetric part is the exterior product of the two vectors, the product of the containedexterior algebra:

$a\wedge b:={\frac {1}{2}}(ab-ba)=-(b\wedge a).$

Then by simple addition:

$ab=a\cdot b+a\wedge b$the ungeneralized or vector form of the geometric product.

The inner and exterior products are associated with familiar concepts from standard vector algebra. Geometrically,$a$and$b$areparallelif their geometric product is equal to their inner product, whereas$a$and$b$areperpendicularif their geometric product is equal to their exterior product. In a geometric algebra for which the square of any nonzero vector is positive, the inner product of two vectors can be identified with thedot productof standard vector algebra. The exterior product of two vectors can be identified with thesigned areaenclosed by aparallelogramthe sides of which are the vectors. Thecross productof two vectors in$3$dimensions with positive-definite quadratic form is closely related to their exterior product.

Most instances of geometric algebras of interest have a nondegenerate quadratic form. If the quadratic form is fullydegenerate,the inner product of any two vectors is always zero, and the geometric algebra is then simply an exterior algebra. Unless otherwise stated, this article will treat only nondegenerate geometric algebras.

The exterior product is naturally extended as an associative bilinear binary operator between any two elements of the algebra, satisfying the identities

${\begin{aligned}1\wedge a_{i}&=a_{i}\wedge 1=a_{i}\\a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r}&={\frac {1}{r!}}\sum _{\sigma \in {\mathfrak {S}}_{r}}\operatorname {sgn} (\sigma )a_{\sigma (1)}a_{\sigma (2)}\cdots a_{\sigma (r)},\end{aligned}}$

where the sum is over all permutations of the indices, with$\operatorname {sgn} (\sigma )$thesign of the permutation,and$a_{i}$are vectors (not general elements of the algebra). Since every element of the algebra can be expressed as the sum of products of this form, this defines the exterior product for every pair of elements of the algebra. It follows from the definition that the exterior product forms analternating algebra.

The equivalent structure equation for Clifford algebra is

$a_{1}a_{2}a_{3}\dots a_{n}=\sum _{i=0}^{[{\frac {n}{2}}]}\sum _{\mu \in {}{\mathcal {C}}}(-1)^{k}\operatorname {Pf} (a_{\mu _{1}}\cdot a_{\mu _{2}},\dots,a_{\mu _{2i-1}}\cdot a_{\mu _{2i}})a_{\mu _{2i+1}}\land \dots \land a_{\mu _{n}}$

where$\operatorname {Pf} (A)$is thePfaffianof⁠$A$⁠and${\textstyle {\mathcal {C}}={\binom {n}{2i}}}$providescombinations,⁠$\mu$⁠,of⁠$n$⁠indices divided into⁠$2i$⁠and⁠$n-2i$⁠parts and⁠$k$⁠is theparityof thecombination.

The Pfaffian provides a metric for the exterior algebra and, as pointed out by Claude Chevalley, Clifford algebra reduces to the exterior algebra with a zero quadratic form.The role the Pfaffian plays can be understood from a geometric viewpoint by developing Clifford algebra fromsimplices.This derivation provides a better connection betweenPascal's triangleandsimplicesbecause it provides an interpretation of the first column of ones.

Blades, grades, and basis

A multivector that is the exterior product of$r$linearly independent vectors is called ablade,and is said to be of grade⁠$r$⁠.A multivector that is the sum of blades of grade$r$is called a (homogeneous) multivector of grade⁠$r$⁠.From the axioms, with closure, every multivector of the geometric algebra is a sum of blades.

Consider a set of$r$linearly independent vectors$\{a_{1},\ldots,a_{r}\}$spanning an⁠$r$⁠-dimensional subspace of the vector space. With these, we can define a realsymmetric matrix(in the same way as aGramian matrix)

$[\mathbf {A} ]_{ij}=a_{i}\cdot a_{j}$

By thespectral theorem,$\mathbf {A}$can be diagonalized todiagonal matrix$\mathbf {D}$by anorthogonal matrix$\mathbf {O}$via

$\sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {A} ]_{kl}[\mathbf {O} ^{\mathrm {T} }]_{lj}=\sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {O} ]_{jl}[\mathbf {A} ]_{kl}=[\mathbf {D} ]_{ij}$

Define a new set of vectors⁠$\{e_{1},\ldots,e_{r}\}$⁠,known as orthogonal basis vectors, to be those transformed by the orthogonal matrix:

$e_{i}=\sum _{j}[\mathbf {O} ]_{ij}a_{j}$

Since orthogonal transformations preserve inner products, it follows that$e_{i}\cdot e_{j}=[\mathbf {D} ]_{ij}$and thus the$\{e_{1},\ldots,e_{r}\}$are perpendicular. In other words, the geometric product of two distinct vectors$e_{i}\neq e_{j}$is completely specified by their exterior product, or more generally

${\begin{array}{rl}e_{1}e_{2}\cdots e_{r}&=e_{1}\wedge e_{2}\wedge \cdots \wedge e_{r}\\&=\left(\sum _{j}[\mathbf {O} ]_{1j}a_{j}\right)\wedge \left(\sum _{j}[\mathbf {O} ]_{2j}a_{j}\right)\wedge \cdots \wedge \left(\sum _{j}[\mathbf {O} ]_{rj}a_{j}\right)\\&=(\det \mathbf {O} )a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r}\end{array}}$

Therefore, every blade of grade$r$can be written as the exterior product of$r$vectors. More generally, if a degenerate geometric algebra is allowed, then the orthogonal matrix is replaced by ablock matrixthat is orthogonal in the nondegenerate block, and the diagonal matrix has zero-valued entries along the degenerate dimensions. If the new vectors of the nondegenerate subspace arenormalizedaccording to

${\widehat {e_{i}}}={\frac {1}{\sqrt {|e_{i}\cdot e_{i}|}}}e_{i},$

then these normalized vectors must square to$+1$or⁠$-1$⁠.BySylvester's law of inertia,the total number of⁠$+1$⁠and the total number of⁠$-1$⁠s along the diagonal matrix is invariant. By extension, the total number$p$of these vectors that square to$+1$and the total number$q$that square to$-1$is invariant. (The total number of basis vectors that square to zero is also invariant, and may be nonzero if the degenerate case is allowed.) We denote this algebra⁠${\mathcal {G}}(p,q)$⁠.For example,${\mathcal {G}}(3,0)$models three-dimensionalEuclidean space,${\mathcal {G}}(1,3)$relativisticspacetimeand${\mathcal {G}}(4,1)$aconformal geometric algebraof a three-dimensional space.

The set of all possible products of$n$orthogonal basis vectors with indices in increasing order, including$1$as the empty product, forms a basis for the entire geometric algebra (an analogue of thePBW theorem). For example, the following is a basis for the geometric algebra⁠${\mathcal {G}}(3,0)$⁠:

$\{1,e_{1},e_{2},e_{3},e_{1}e_{2},e_{2}e_{3},e_{3}e_{1},e_{1}e_{2}e_{3}\}$

A basis formed this way is called astandard basisfor the geometric algebra, and any other orthogonal basis for$V$will produce another standard basis. Each standard basis consists of$2^{n}$elements. Every multivector of the geometric algebra can be expressed as a linear combination of the standard basis elements. If the standard basis elements are$\{B_{i}\mid i\in S\}$with$S$being an index set, then the geometric product of any two multivectors is

$\left(\sum _{i}\alpha _{i}B_{i}\right)\left(\sum _{j}\beta _{j}B_{j}\right)=\sum _{i,j}\alpha _{i}\beta _{j}B_{i}B_{j}.$

The terminology "$k$-vector "is often encountered to describe multivectors containing elements of only one grade. In higher dimensional space, some such multivectors are not blades (cannot be factored into the exterior product of$k$vectors). By way of example,$e_{1}\wedge e_{2}+e_{3}\wedge e_{4}$in${\mathcal {G}}(4,0)$cannot be factored; typically, however, such elements of the algebra do not yield to geometric interpretation as objects, although they may represent geometric quantities such as rotations. Only⁠$0$⁠-,⁠$1$⁠-,⁠$(n-1)$⁠- and⁠$n$⁠-vectors are always blades in⁠$n$⁠-space.

Versor

A⁠$k$⁠-versor is a multivector that can be expressed as the geometric product of$k$invertible vectors.Unit quaternions (originally called versors by Hamilton) may be identified with rotors in 3D space in much the same way as real 2D rotors subsume complex numbers; for the details refer to Dorst.

Some authors use the term "versor product" to refer to the frequently occurring case where an operand is "sandwiched" between operators. The descriptions for rotations and reflections, including their outermorphisms, are examples of such sandwiching. These outermorphisms have a particularly simple algebraic form.Specifically, a mapping of vectors of the form

$V\to V:a\mapsto RaR^{-1}$extends to the outermorphism${\mathcal {G}}(V)\to {\mathcal {G}}(V):A\mapsto RAR^{-1}.$

Since both operators and operand are versors there is potential for alternative examples such as rotating a rotor or reflecting a spinor always provided that some geometrical or physical significance can be attached to such operations.

By theCartan–Dieudonné theoremwe have that every isometry can be given as reflections in hyperplanes and since composed reflections provide rotations then we have that orthogonal transformations are versors.

In group terms, for a real, non-degenerate⁠${\mathcal {G}}(p,q)$⁠,having identified the group${\mathcal {G}}^{\times }$as the group of all invertible elements of⁠${\mathcal {G}}$⁠,Lundholm gives a proof that the "versor group"$\{v_{1}v_{2}\cdots v_{k}\in {\mathcal {G}}\mid v_{i}\in V^{\times }\}$(the set of invertible versors) is equal to the Lipschitz group$\Gamma$(a.k.a.Clifford group, although Lundholm deprecates this usage).

Subgroups of the Lipschitz group

We denote the grade involution as⁠${\widehat {S}}$⁠and reversion as⁠${\widetilde {S}}$⁠.

Although the Lipschitz group (defined as⁠$\{S\in {\mathcal {G}}^{\times }\mid {\widehat {S}}VS^{-1}\subseteq V\}$⁠) and the versor group (defined as⁠$\textstyle \{\prod _{i=0}^{k}v_{i}\mid v_{i}\in V^{\times },k\in \mathbb {N} \}$⁠) have divergent definitions, they are the same group. Lundholm defines the⁠$\operatorname {Pin}$⁠,⁠$\operatorname {Spin}$⁠,and⁠$\operatorname {Spin} ^{+}$⁠subgroups of the Lipschitz group.

Subgroup	Definition	GA term
$\Gamma$	$\{S\in {\mathcal {G}}^{\times }\mid {\widehat {S}}VS^{-1}\subseteq V\}$	versors
$\operatorname {Pin}$	$\{S\in \Gamma \mid S{\widetilde {S}}=\pm 1\}$	unit versors
$\operatorname {Spin}$	${\operatorname {Pin} }\cap {\mathcal {G}}^{[0]}$	even unit versors
$\operatorname {Spin} ^{+}$	$\{S\in \operatorname {Spin} \mid S{\widetilde {S}}=1\}$	rotors

Multiple analyses of spinors use GA as a representation.

Grade projection

A⁠$\mathbb {Z}$⁠-graded vector spacestructure can be established on a geometric algebra by use of the exterior product that is naturally induced by the geometric product.

Since the geometric product and the exterior product are equal on orthogonal vectors, this grading can be conveniently constructed by using an orthogonal basis⁠$\{e_{1},\ldots,e_{n}\}$⁠.

Elements of the geometric algebra that are scalar multiples of$1$are of grade$0$and are calledscalars.Elements that are in the span of$\{e_{1},\ldots,e_{n}\}$are of grade⁠$1$⁠and are the ordinary vectors. Elements in the span of$\{e_{i}e_{j}\mid 1\leq i<j\leq n\}$are of grade$2$and are the bivectors. This terminology continues through to the last grade of⁠$n$⁠-vectors. Alternatively,⁠$n$⁠-vectors are calledpseudoscalars,⁠$(n-1)$⁠-vectors are called pseudovectors, etc. Many of the elements of the algebra are not graded by this scheme since they are sums of elements of differing grade. Such elements are said to be ofmixed grade.The grading of multivectors is independent of the basis chosen originally.

This is a grading as a vector space, but not as an algebra. Because the product of an⁠$r$⁠-blade and an⁠$s$⁠-blade is contained in the span of$0$through⁠$r+s$⁠-blades, the geometric algebra is afiltered algebra.

A multivector$A$may be decomposed with thegrade-projection operator⁠$\langle A\rangle _{r}$⁠,which outputs the grade-⁠$r$⁠portion of⁠$A$⁠.As a result:

$A=\sum _{r=0}^{n}\langle A\rangle _{r}$

As an example, the geometric product of two vectors$ab=a\cdot b+a\wedge b=\langle ab\rangle _{0}+\langle ab\rangle _{2}$since$\langle ab\rangle _{0}=a\cdot b$and$\langle ab\rangle _{2}=a\wedge b$and⁠$\langle ab\rangle _{i}=0$⁠,for$i$other than$0$and⁠$2$⁠.

A multivector$A$may also be decomposed into even and odd components, which may respectively be expressed as the sum of the even and the sum of the odd grade components above:

$A^{[0]}=\langle A\rangle _{0}+\langle A\rangle _{2}+\langle A\rangle _{4}+\cdots$

$A^{[1]}=\langle A\rangle _{1}+\langle A\rangle _{3}+\langle A\rangle _{5}+\cdots$

This is the result of forgetting structure from a⁠$\mathrm {Z}$⁠-graded vector spaceto⁠$\mathrm {Z} _{2}$⁠-graded vector space.The geometric product respects this coarser grading. Thus in addition to being a⁠$\mathrm {Z} _{2}$⁠-graded vector space,the geometric algebra is a⁠$\mathrm {Z} _{2}$⁠-graded algebra,a.k.a.asuperalgebra.

Restricting to the even part, the product of two even elements is also even. This means that the even multivectors defines aneven subalgebra.The even subalgebra of an⁠$n$⁠-dimensional geometric algebra isalgebra-isomorphic(without preserving either filtration or grading) to a full geometric algebra of$(n-1)$dimensions. Examples include${\mathcal {G}}^{[0]}(2,0)\cong {\mathcal {G}}(0,1)$and⁠${\mathcal {G}}^{[0]}(1,3)\cong {\mathcal {G}}(3,0)$⁠.

Representation of subspaces

See also:Grassmannian

Geometric algebra represents subspaces of$V$as blades, and so they coexist in the same algebra with vectors from⁠$V$⁠.A⁠$k$⁠-dimensional subspace$W$of$V$is represented by taking an orthogonal basis$\{b_{1},b_{2},\ldots,b_{k}\}$and using the geometric product to form theblade⁠$D=b_{1}b_{2}\cdots b_{k}$⁠.There are multiple blades representing⁠$W$⁠;all those representing$W$are scalar multiples of⁠$D$⁠.These blades can be separated into two sets: positive multiples of$D$and negative multiples of⁠$D$⁠.The positive multiples of$D$are said to havethe sameorientationas⁠$D$⁠,and the negative multiples theopposite orientation.

Blades are important since geometric operations such as projections, rotations and reflections depend on the factorability via the exterior product that (the restricted class of)⁠$n$⁠-blades provide but that (the generalized class of) grade-⁠$n$⁠multivectors do not when⁠$n\geq 4$⁠.

Unit pseudoscalars

Unit pseudoscalars are blades that play important roles in GA. Aunit pseudoscalarfor a non-degenerate subspace$W$of$V$is a blade that is the product of the members of an orthonormal basis for⁠$W$⁠.It can be shown that if$I$and$I'$are both unit pseudoscalars for⁠$W$⁠,then$I=\pm I'$and⁠$I^{2}=\pm 1$⁠.If one doesn't choose an orthonormal basis for⁠$W$⁠,then thePlücker embeddinggives a vector in the exterior algebra but only up to scaling. Using the vector space isomorphism between the geometric algebra and exterior algebra, this gives the equivalence class of$\alpha I$for all⁠$\alpha \neq 0$⁠.Orthonormality gets rid of this ambiguity except for the signs above.

Suppose the geometric algebra${\mathcal {G}}(n,0)$with the familiar positive definite inner product on$\mathbb {R} ^{n}$is formed. Given a plane (two-dimensional subspace) of⁠$\mathbb {R} ^{n}$⁠,one can find an orthonormal basis$\{b_{1},b_{2}\}$spanning the plane, and thus find a unit pseudoscalar$I=b_{1}b_{2}$representing this plane. The geometric product of any two vectors in the span of$b_{1}$and$b_{2}$lies in⁠$\{\alpha _{0}+\alpha _{1}I\mid \alpha _{i}\in \mathbb {R} \}$⁠,that is, it is the sum of a⁠$0$⁠-vector and a⁠$2$⁠-vector.

By the properties of the geometric product,⁠$I^{2}=b_{1}b_{2}b_{1}b_{2}=-b_{1}b_{2}b_{2}b_{1}=-1$⁠.The resemblance to theimaginary unitis not incidental: the subspace$\{\alpha _{0}+\alpha _{1}I\mid \alpha _{i}\in \mathbb {R} \}$is⁠$\mathbb {R}$⁠-algebra isomorphic to thecomplex numbers.In this way, a copy of the complex numbers is embedded in the geometric algebra for each two-dimensional subspace of$V$on which the quadratic form is definite.

It is sometimes possible to identify the presence of an imaginary unit in a physical equation. Such units arise from one of the many quantities in the real algebra that square to⁠$-1$⁠,and these have geometric significance because of the properties of the algebra and the interaction of its various subspaces.

In⁠${\mathcal {G}}(3,0)$⁠,a further familiar case occurs. Given a standard basis consisting of orthonormal vectors$e_{i}$of⁠$V$⁠,the set ofall⁠$2$⁠-vectors is spanned by

$\{e_{3}e_{2},e_{1}e_{3},e_{2}e_{1}\}.$

Labelling these⁠$i$⁠,$j$and$k$(momentarily deviating from our uppercase convention), the subspace generated by⁠$0$⁠-vectors and⁠$2$⁠-vectors is exactly⁠$\{\alpha _{0}+i\alpha _{1}+j\alpha _{2}+k\alpha _{3}\mid \alpha _{i}\in \mathbb {R} \}$⁠.This set is seen to be the even subalgebra of⁠${\mathcal {G}}(3,0)$⁠,and furthermore is isomorphic as an⁠$\mathbb {R}$⁠-algebra to thequaternions,another important algebraic system.

Extensions of the inner and exterior products

It is common practice to extend the exterior product on vectors to the entire algebra. This may be done through the use of the above mentionedgrade projectionoperator:

$C\wedge D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{r+s}$(theexterior product)

This generalization is consistent with the above definition involving antisymmetrization. Another generalization related to the exterior product is the commutator product:

$C\times D:={\tfrac {1}{2}}(CD-DC)$(thecommutator product)

The regressive product is the dual of the exterior product (respectively corresponding to the "meet" and "join" in this context).The dual specification of elements permits, for blades⁠$C$⁠and⁠$D$⁠,the intersection (or meet) where the duality is to be taken relative to the a blade containing both⁠$C$⁠and⁠$D$⁠(the smallest such blade being the join).

$C\vee D:=((CI^{-1})\wedge (DI^{-1}))I$

with⁠$I$⁠the unit pseudoscalar of the algebra. The regressive product, like the exterior product, is associative.

The inner product on vectors can also be generalized, but in more than one non-equivalent way. The paper (Dorst 2002) gives a full treatment of several different inner products developed for geometric algebras and their interrelationships, and the notation is taken from there. Many authors use the same symbol as for the inner product of vectors for their chosen extension (e.g. Hestenes and Perwass). No consistent notation has emerged.

Among these several different generalizations of the inner product on vectors are:

$C\;\rfloor \;D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{s-r}$(theleft contraction)

$C\;\lfloor \;D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{r-s}$(theright contraction)

$C*D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{0}$(thescalar product)

$C\bullet D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{|s-r|}$(the "(fat) dot" product)

Dorst (2002)makes an argument for the use of contractions in preference to Hestenes's inner product; they are algebraically more regular and have cleaner geometric interpretations. A number of identities incorporating the contractions are valid without restriction of their inputs. For example,

$C\;\rfloor \;D=(C\wedge (DI^{-1}))I$

$C\;\lfloor \;D=I((I^{-1}C)\wedge D)$

$(A\wedge B)*C=A*(B\;\rfloor \;C)$

$C*(B\wedge A)=(C\;\lfloor \;B)*A$

$A\;\rfloor \;(B\;\rfloor \;C)=(A\wedge B)\;\rfloor \;C$

$(A\;\rfloor \;B)\;\lfloor \;C=A\;\rfloor \;(B\;\lfloor \;C).$

Benefits of using the left contraction as an extension of the inner product on vectors include that the identity$ab=a\cdot b+a\wedge b$is extended to$aB=a\;\rfloor \;B+a\wedge B$for any vector$a$and multivector⁠$B$⁠,and that theprojectionoperation${\mathcal {P}}_{b}(a)=(a\cdot b^{-1})b$is extended to${\mathcal {P}}_{B}(A)=(A\;\rfloor \;B^{-1})\;\rfloor \;B$for any blade$B$and any multivector$A$(with a minor modification to accommodate null⁠$B$⁠,givenbelow).

Dual basis

Let$\{e_{1},\ldots,e_{n}\}$be a basis of⁠$V$⁠,i.e. a set of$n$linearly independent vectors that span the⁠$n$⁠-dimensional vector space⁠$V$⁠.The basis that is dual to$\{e_{1},\ldots,e_{n}\}$is the set of elements of thedual vector space$V^{*}$that forms abiorthogonal systemwith this basis, thus being the elements denoted$\{e^{1},\ldots,e^{n}\}$satisfying

$e^{i}\cdot e_{j}=\delta ^{i}{}_{j},$

where$\delta$is theKronecker delta.

Given a nondegenerate quadratic form on⁠$V$⁠,$V^{*}$becomes naturally identified with⁠$V$⁠,and the dual basis may be regarded as elements of⁠$V$⁠,but are not in general the same set as the original basis.

Given further a GA of⁠$V$⁠,let

$I=e_{1}\wedge \cdots \wedge e_{n}$

be the pseudoscalar (which does not necessarily square to⁠$\pm 1$⁠) formed from the basis⁠$\{e_{1},\ldots,e_{n}\}$⁠.The dual basis vectors may be constructed as

$e^{i}=(-1)^{i-1}(e_{1}\wedge \cdots \wedge {\check {e}}_{i}\wedge \cdots \wedge e_{n})I^{-1},$

where the${\check {e}}_{i}$denotes that the⁠$i$⁠th basis vector is omitted from the product.

A dual basis is also known as areciprocal basisor reciprocal frame.

A major usage of a dual basis is to separate vectors into components. Given a vector⁠$a$⁠,scalar components$a^{i}$can be defined as

$a^{i}=a\cdot e^{i}\,$

in terms of which$a$can be separated into vector components as

$a=\sum _{i}a^{i}e_{i}\.$

We can also define scalar components$a_{i}$as

$a_{i}=a\cdot e_{i}\,$

in terms of which$a$can be separated into vector components in terms of the dual basis as

$a=\sum _{i}a_{i}e^{i}\.$

A dual basis as defined above for the vector subspace of a geometric algebra can be extended to cover the entire algebra.For compactness, we'll use a single capital letter to represent an ordered set of vector indices. I.e., writing

$J=(j_{1},\dots,j_{n})\,$

where⁠$j_{1}<j_{2}<\dots <j_{n}$⁠, we can write a basis blade as

$e_{J}=e_{j_{1}}\wedge e_{j_{2}}\wedge \cdots \wedge e_{j_{n}}\.$

The corresponding reciprocal blade has the indices in opposite order:

$e^{J}=e^{j_{n}}\wedge \cdots \wedge e^{j_{2}}\wedge e^{j_{1}}\.$

Similar to the case above with vectors, it can be shown that

$e^{J}*e_{K}=\delta _{K}^{J}\,$

where$*$is the scalar product.

With$A$a multivector, we can define scalar components as

$A^{ij\cdots k}=(e^{k}\wedge \cdots \wedge e^{j}\wedge e^{i})*A\,$

in terms of which$A$can be separated into component blades as

$A=\sum _{i<j<\cdots <k}A^{ij\cdots k}e_{i}\wedge e_{j}\wedge \cdots \wedge e_{k}\.$

We can alternatively define scalar components

$A_{ij\cdots k}=(e_{k}\wedge \cdots \wedge e_{j}\wedge e_{i})*A\,$

in terms of which$A$can be separated into component blades as

$A=\sum _{i<j<\cdots <k}A_{ij\cdots k}e^{i}\wedge e^{j}\wedge \cdots \wedge e^{k}\.$

Linear functions

Although a versor is easier to work with because it can be directly represented in the algebra as a multivector, versors are a subgroup oflinear functionson multivectors, which can still be used when necessary. The geometric algebra of an⁠$n$⁠-dimensional vector space is spanned by a basis of$2^{n}$elements. If a multivector is represented by a$2^{n}\times 1$realcolumn matrixof coefficients of a basis of the algebra, then all linear transformations of the multivector can be expressed as thematrix multiplicationby a$2^{n}\times 2^{n}$real matrix. However, such a general linear transformation allows arbitrary exchanges among grades, such as a "rotation" of a scalar into a vector, which has no evident geometric interpretation.

A general linear transformation from vectors to vectors is of interest. With the natural restriction to preserving the induced exterior algebra, theoutermorphismof the linear transformation is the uniqueextension of the versor. If$f$is a linear function that maps vectors to vectors, then its outermorphism is the function that obeys the rule

${\underline {\mathsf {f}}}(a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r})=f(a_{1})\wedge f(a_{2})\wedge \cdots \wedge f(a_{r})$

for a blade, extended to the whole algebra through linearity.

Modeling geometries

Although a lot of attention has been placed on CGA, it is to be noted that GA is not just one algebra, it is one of a family of algebras with the same essential structure.

Vector space model

Main article:Comparison of vector algebra and geometric algebra

Theeven subalgebraof${\mathcal {G}}(2,0)$is isomorphic to thecomplex numbers,as may be seen by writing a vector$P$in terms of its components in an orthonormal basis and left multiplying by the basis vector⁠$e_{1}$⁠,yielding

$Z=e_{1}P=e_{1}(xe_{1}+ye_{2})=x(1)+y(e_{1}e_{2}),$

where we identify$i\mapsto e_{1}e_{2}$since

$(e_{1}e_{2})^{2}=e_{1}e_{2}e_{1}e_{2}=-e_{1}e_{1}e_{2}e_{2}=-1.$

Similarly, the even subalgebra of${\mathcal {G}}(3,0)$with basis$\{1,e_{2}e_{3},e_{3}e_{1},e_{1}e_{2}\}$is isomorphic to thequaternionsas may be seen by identifying⁠$i\mapsto -e_{2}e_{3}$⁠,$j\mapsto -e_{3}e_{1}$and⁠$k\mapsto -e_{1}e_{2}$⁠.

Everyassociative algebrahas a matrix representation; replacing the three Cartesian basis vectors by thePauli matricesgives a representation of⁠${\mathcal {G}}(3,0)$⁠:

${\begin{aligned}e_{1}=\sigma _{1}=\sigma _{x}&={\begin{pmatrix}0&1\\1&0\end{pmatrix}}\\e_{2}=\sigma _{2}=\sigma _{y}&={\begin{pmatrix}0&-i\\i&0\end{pmatrix}}\\e_{3}=\sigma _{3}=\sigma _{z}&={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}\,.\end{aligned}}$

Dotting the "Pauli vector"(adyad):

$\sigma =\sigma _{1}e_{1}+\sigma _{2}e_{2}+\sigma _{3}e_{3}$with arbitrary vectors$a$and$b$and multiplying through gives:

$(\sigma \cdot a)(\sigma \cdot b)=a\cdot b+a\wedge b$(Equivalently, by inspection,⁠$a\cdot b+i\sigma \cdot (a\times b)$⁠)

Spacetime model

In physics, the main applications are the geometric algebra ofMinkowski 3+1 spacetime,⁠${\mathcal {G}}(1,3)$⁠,calledspacetime algebra(STA),or less commonly,⁠${\mathcal {G}}(3,0)$⁠,interpreted thealgebra of physical space(APS).

While in STA, points of spacetime are represented simply by vectors, in APS, points of⁠$(3+1)$⁠-dimensional spacetime are instead represented byparavectors,a three-dimensional vector (space) plus a one-dimensional scalar (time).

In spacetime algebra the electromagnetic field tensor has a bivector representation⁠${F}=({E}+ic{B})\gamma _{0}$⁠.Here, the$i=\gamma _{0}\gamma _{1}\gamma _{2}\gamma _{3}$is the unit pseudoscalar (or four-dimensional volume element),$\gamma _{0}$is the unit vector in time direction, and$E$and$B$are the classic electric and magnetic field vectors (with a zero time component). Using thefour-current⁠${J}$⁠,Maxwell's equationsthen become

Formulation	Homogeneous equations	Non-homogeneous equations
Fields	$DF=\mu _{0}J$
	$D\wedge F=0$	$D~\rfloor ~F=\mu _{0}J$
Potentials (any gauge)	$F=D\wedge A$	$D~\rfloor ~(D\wedge A)=\mu _{0}J$
Potentials (Lorenz gauge)	$F=DA$ $D~\rfloor ~A=0$	$D^{2}A=\mu _{0}J$

In geometric calculus, juxtaposition of vectors such as in$DF$indicate the geometric product and can be decomposed into parts as⁠$DF=D~\rfloor ~F+D\wedge F$⁠.Here$D$is the covector derivative in any spacetime and reduces to$\nabla$in flat spacetime. Where$\bigtriangledown$plays a role in Minkowski⁠$4$⁠-spacetime which is synonymous to the role of$\nabla$in Euclidean⁠$3$⁠-space and is related to thed'Alembertianby⁠$\Box =\bigtriangledown ^{2}$⁠.Indeed, given an observer represented by a future pointing timelike vector$\gamma _{0}$we have

$\gamma _{0}\cdot \bigtriangledown ={\frac {1}{c}}{\frac {\partial }{\partial t}}$

$\gamma _{0}\wedge \bigtriangledown =\nabla$

Boostsin this Lorentzian metric space have the same expression$e^{\beta }$as rotation in Euclidean space, where${\beta }$is the bivector generated by the time and the space directions involved, whereas in the Euclidean case it is the bivector generated by the two space directions, strengthening the "analogy" to almost identity.

TheDirac matricesare a representation of⁠${\mathcal {G}}(1,3)$⁠,showing the equivalence with matrix representations used by physicists.

Homogeneous models

Homogeneous models generally refer to a projective representation in which the elements of the one-dimensional subspaces of a vector space represent points of a geometry.

In a geometric algebra of a space of$n$dimensions, the rotors represent a set of transformations with$n(n-1)/2$degrees of freedom, corresponding to rotations – for example,$3$when$n=3$and$6$when⁠$n=4$⁠.Geometric algebra is often used to model aprojective space,i.e. as ahomogeneous model:a point, line, plane, etc. is represented by an equivalence class of elements of the algebra that differ by an invertible scalar factor.

The rotors in a space of dimension$n+1$have$n(n-1)/2+n$degrees of freedom, the same as the number of degrees of freedom in the rotations and translations combined for an⁠$n$⁠-dimensional space.

This is the case inProjective Geometric Algebra(PGA), which is usedto representEuclidean isometriesin Euclidean geometry (thereby covering the large majority of engineering applications of geometry). In this model, a degenerate dimension is added to the three Euclidean dimensions to form the algebra⁠${\mathcal {G}}(3,0,1)$⁠.With a suitable identification of subspaces to represent points, lines and planes, the versors of this algebra represent all proper Euclidean isometries, which are alwaysscrew motionsin 3-dimensional space, along with all improper Euclidean isometries, which includes reflections, rotoreflections, transflections, and point reflections.

PGA combines${\mathcal {G}}(3,0,1)$with acomplementoperator to obtain join, meet, distance, and angle formulas.In effect, the complement switches basis vectors that are present and absent in the expression of each term of the algebraic representation. For example, in the PGA or 3-dimensional space, the complement of the line${\boldsymbol {e}}_{12}$is the line⁠${\boldsymbol {e}}_{03}$⁠,because${\boldsymbol {e}}_{0}$and${\boldsymbol {e}}_{3}$are basis elements that arenotcontained in${\boldsymbol {e}}_{12}$butarecontained in⁠${\boldsymbol {e}}_{03}$⁠.In the PGA of 2-dimensional space, the complement of${\boldsymbol {e}}_{12}$is⁠${\boldsymbol {e}}_{0}$⁠,since there is no${\boldsymbol {e}}_{3}$element.

PGA is a widely used system that combines geometric algebra with homogeneous representations in geometry, but there exist several other such systems. The conformal model discussed below is homogeneous, as is "Conic Geometric Algebra",and seePlane-based geometric algebrafor discussion of homogeneous models of elliptic and hyperbolic geometry compared with the Euclidean geometry derived from PGA.

Conformal model

Main article:Conformal geometric algebra

Working within GA, Euclidean space$\mathbb {E} ^{3}$(along with a conformal point at infinity) is embedded projectively in the CGA${\mathcal {G}}(4,1)$via the identification of Euclidean points with 1D subspaces in the 4D null cone of the 5D CGA vector subspace. This allows all conformal transformations to be performed as rotations and reflections and iscovariant,extending incidence relations of projective geometry to rounds objects such as circles and spheres.

Specifically, we add orthogonal basis vectors$e_{+}$and$e_{-}$such that$e_{+}^{2}=+1$and$e_{-}^{2}=-1$to the basis of the vector space that generates${\mathcal {G}}(3,0)$and identifynull vectors

$n_{\text{o}}={\tfrac {1}{2}}(e_{-}-e_{+})$as the point at the origin and

$n_{\infty }=e_{-}+e_{+}$as a conformal point at infinity (seeCompactification), giving

$n_{\infty }\cdot n_{\text{o}}=-1.$

(Some authors set$e_{4}=n_{\text{o}}$and⁠$e_{5}=n_{\infty }$⁠.) This procedure has some similarities to the procedure for working withhomogeneous coordinatesin projective geometry, and in this case allows the modeling ofEuclidean transformationsof$\mathbb {R} ^{3}$asorthogonal transformationsof a subset of⁠$\mathbf {R} ^{4,1}$⁠.

A fast changing and fluid area of GA, CGA is also being investigated for applications to relativistic physics.

Table of models

Note in this list that⁠$p$⁠and⁠$q$⁠can be swapped and the same name applies; for example, withrelativelylittle change occurring, seesign convention.For example,${\mathcal {G}}(3,1,0)$and${\mathcal {G}}(1,3,0)$arebothreferred to as Spacetime Algebra.

Name	Signature	Blades, e.g., oriented geometric objects that algebra can represent	Rotors, e.g.,orientation-preserving transformations that the algebra can represent	Notes
Vectorspace GA, VGA Algebra of Physical Space,APS	${\mathcal {G}}(3,0,0)$	Planes and lines through the origin	Rotations, eg$\mathrm {SO} (3)$	First GA to be discovered
Projective GA, PGA, Rigid GA, RGA,Plane-based GA	${\mathcal {G}}(3,0,1)$	Planes, lines, and points anywhere in space	Rotations and translations, e.g.,rigid motions,$\mathrm {SE} (3)$aka$\mathrm {SO} (3,0,1)$	Slight modifications to the signature allow for the modelling of hyperbolic and elliptic space, see main article. Cannot model the entire "projective" group.
Spacetime Algebra,STA	${\mathcal {G}}(3,1,0)$	Volumes, planes and lines through the origin in spacetime	Rotations and spacetime boosts, e.g.⁠$\mathrm {SO} (3,1)$⁠,theLorentz group	Basis forGauge Theory Gravity.
Spacetime Algebra Projectivized,STAP	${\mathcal {G}}(3,1,1)$	Volumes, planes, lines, and points (events) in spacetime	Rotations, translations, and spacetime boosts (Poincare group)
Conformal GA,CGA	${\mathcal {G}}(4,1,0)$	Spheres, circles, point pairs (or dipoles), round points, flat points, lines, and planes anywhere in space	Transformations of space that preserve angles (Conformal group⁠$\mathrm {SO} (4,1)$⁠)
Conformal Spacetime Algebra,CSTA	${\mathcal {G}}(4,2,0)$	Spheres, circles, planes, lines, light-cones, trajectories of objects with constant acceleration, all in spacetime	Conformal transformations of spacetime, e.g. transformations that preserverapidityalong arclengths through spacetime	Related toTwistor theory.
Mother Algebra	${\mathcal {G}}(3,3,0)$	Unknown	Projective group
GA for Conics, GAC Quadric Conformal 2D GA QC2GA	${\mathcal {G}}(5,3,0)$	Points, point pair/triple/quadruple, Conic, Pencil of up to 6 independent conics.	Reflections, translations, rotations, dilations, others	Conics can be created from control points and pencils of conics.
Quadric Conformal GA, QCGA	${\mathcal {G}}(9,6,0)$	Points, tuples of up to 8 points, quadric surfaces, conics, conics on quadratic surfaces (such asSpherical conic), pencils of up to 9 quadric surfaces.	Reflections, translations, rotations, dilations, others	Quadric surfaces can be created from control points and their surface normals can be determined.
Double Conformal Geometric Algebra (DCGA)	${\mathcal {G}}(8,2,0)$	Points, Darboux Cyclides, quadrics surfaces	Reflections, translations, rotations, dilations, others	Uses bivectors of two independent CGA basis to represents 5×5 symmetric "matrices" of 15 unique coefficients. This is at the cost of the ability to perform intersections and construction by points.

Geometric interpretation in the vector space model

Projection and rejection

In 3D space, a bivector$a\land b$defines a 2D plane subspace (light blue, extends infinitely in indicated directions). Any vector$c$in 3D space can be decomposed into its projection$c_{\Vert }$onto a plane and its rejection$c_{\perp }$from this plane.

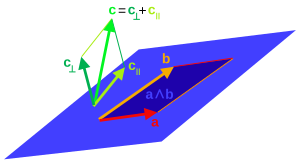
For any vector$a$and any invertible vector⁠$m$⁠,

$a=amm^{-1}=(a\cdot m+a\wedge m)m^{-1}=a_{\|m}+a_{\perp m},$

where theprojectionof$a$onto$m$(or the parallel part) is

$a_{\|m}=(a\cdot m)m^{-1}$

and therejectionof$a$from$m$(or the orthogonal part) is

$a_{\perp m}=a-a_{\|m}=(a\wedge m)m^{-1}.$

Using the concept of a⁠$k$⁠-blade⁠$B$⁠as representing a subspace of⁠$V$⁠and every multivector ultimately being expressed in terms of vectors, this generalizes to projection of a general multivector onto any invertible⁠$k$⁠-blade⁠$B$⁠as

${\mathcal {P}}_{B}(A)=(A\;\rfloor \;B)\;\rfloor \;B^{-1},$

with the rejection being defined as

${\mathcal {P}}_{B}^{\perp }(A)=A-{\mathcal {P}}_{B}(A).$

The projection and rejection generalize to null blades$B$by replacing the inverse$B^{-1}$with the pseudoinverse$B^{+}$with respect to the contractive product.The outcome of the projection coincides in both cases for non-null blades.For null blades⁠$B$⁠,the definition of the projection given here with the first contraction rather than the second being onto the pseudoinverse should be used,as only then is the result necessarily in the subspace represented by⁠$B$⁠. The projection generalizes through linearity to general multivectors⁠$A$⁠.The projection is not linear in⁠$B$⁠and does not generalize to objects⁠$B$⁠that are not blades.

Reflection

Simple reflectionsin a hyperplane are readily expressed in the algebra through conjugation with a single vector. These serve to generate the group of generalrotoreflectionsandrotations.

Reflection of vector$c$along a vector⁠$m$⁠.Only the component of$c$parallel to$m$is negated.

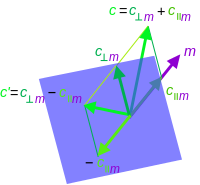
The reflection$c'$of a vector$c$along a vector⁠$m$⁠,or equivalently in the hyperplane orthogonal to⁠$m$⁠,is the same as negating the component of a vector parallel to⁠$m$⁠.The result of the reflection will be

$c'={-c_{\|m}+c_{\perp m}}={-(c\cdot m)m^{-1}+(c\wedge m)m^{-1}}={(-m\cdot c-m\wedge c)m^{-1}}=-mcm^{-1}$

This is not the most general operation that may be regarded as a reflection when the dimension⁠$n\geq 4$⁠.A general reflection may be expressed as the composite of any odd number of single-axis reflections. Thus, a general reflection$a'$of a vector$a$may be written

$a\mapsto a'=-MaM^{-1},$

where

$M=pq\cdots r$and$M^{-1}=(pq\cdots r)^{-1}=r^{-1}\cdots q^{-1}p^{-1}.$

If we define the reflection along a non-null vector$m$of the product of vectors as the reflection of every vector in the product along the same vector, we get for any product of an odd number of vectors that, by way of example,

$(abc)'=a'b'c'=(-mam^{-1})(-mbm^{-1})(-mcm^{-1})=-ma(m^{-1}m)b(m^{-1}m)cm^{-1}=-mabcm^{-1}\,$

and for the product of an even number of vectors that

$(abcd)'=a'b'c'd'=(-mam^{-1})(-mbm^{-1})(-mcm^{-1})(-mdm^{-1})=mabcdm^{-1}.$

Using the concept of every multivector ultimately being expressed in terms of vectors, the reflection of a general multivector$A$using any reflection versor$M$may be written

$A\mapsto M\alpha (A)M^{-1},$

where$\alpha$is theautomorphismofreflection through the originof the vector space (⁠$v\mapsto -v$⁠) extended through linearity to the whole algebra.

Rotations

A rotor that rotates vectors in a plane rotates vectors through angle⁠$\theta$⁠,that is$x\mapsto R_{\theta }x{\widetilde {R}}_{\theta }$is a rotation of$x$through angle⁠$\theta$⁠.The angle between$u$and$v$is⁠$\theta /2$⁠.Similar interpretations are valid for a general multivector$X$instead of the vector⁠$x$⁠.

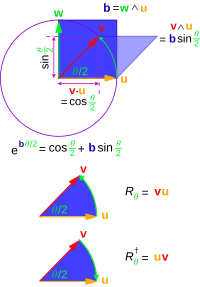
If we have a product of vectors$R=a_{1}a_{2}\cdots a_{r}$then we denote the reverse as

${\widetilde {R}}=a_{r}\cdots a_{2}a_{1}.$

As an example, assume that$R=ab$we get

$R{\widetilde {R}}=abba=ab^{2}a=a^{2}b^{2}=ba^{2}b=baab={\widetilde {R}}R.$

Scaling$R$so that$R{\widetilde {R}}=1$then

$(Rv{\widetilde {R}})^{2}=Rv^{2}{\widetilde {R}}=v^{2}R{\widetilde {R}}=v^{2}$

so$Rv{\widetilde {R}}$leaves the length of$v$unchanged. We can also show that

$(Rv_{1}{\widetilde {R}})\cdot (Rv_{2}{\widetilde {R}})=v_{1}\cdot v_{2}$

so the transformation$Rv{\widetilde {R}}$preserves both length and angle. It therefore can be identified as a rotation or rotoreflection;$R$is called arotorif it is aproper rotation(as it is if it can be expressed as a product of an even number of vectors) and is an instance of what is known in GA as aversor.

There is a general method for rotating a vector involving the formation of a multivector of the form$R=e^{-B\theta /2}$that produces a rotation$\theta$in theplaneand with the orientation defined by a⁠$2$⁠-blade⁠$B$⁠.

Rotors are a generalization of quaternions to⁠$n$⁠-dimensional spaces.

Examples and applications

Hypervolume of a parallelotope spanned by vectors

For vectors⁠$a$⁠and⁠$b$⁠spanning a parallelogram we have

$a\wedge b=((a\wedge b)b^{-1})b=a_{\perp b}b$

with the result that⁠$a\wedge b$⁠is linear in the product of the "altitude" and the "base" of the parallelogram, that is, its area.

Similar interpretations are true for any number of vectors spanning an⁠$n$⁠-dimensionalparallelotope;the exterior product of vectors⁠$a_{1},a_{2},\ldots,a_{n}$⁠,that is⁠$\textstyle \bigwedge _{i=1}^{n}a_{i}$⁠,has a magnitude equal to the volume of the⁠$n$⁠-parallelotope. An⁠$n$⁠-vector does not necessarily have a shape of a parallelotope – this is a convenient visualization. It could be any shape, although the volume equals that of the parallelotope.

Intersection of a line and a plane

A line L defined by points T and P (which we seek) and a plane defined by a bivector B containing points P and Q.

We may define the line parametrically by⁠$p=t+\alpha \ v$⁠,where⁠$p$⁠and⁠$t$⁠are position vectors for points P and T and⁠$v$⁠is the direction vector for the line.

Then

$B\wedge (p-q)=0$and$B\wedge (t+\alpha v-q)=0$

so

$\alpha ={\frac {B\wedge (q-t)}{B\wedge v}}$

and

$p=t+\left({\frac {B\wedge (q-t)}{B\wedge v}}\right)v.$

Rotating systems

A rotational quantity such astorqueorangular momentumis described in geometric algebra as a bivector. Suppose a circular path in an arbitrary plane containing orthonormal vectors⁠${\widehat {u}}$⁠and⁠${\widehat {\ \!v}}$⁠is parameterized by angle.

$\mathbf {r} =r({\widehat {u}}\cos \theta +{\widehat {\ \!v}}\sin \theta )=r{\widehat {u}}(\cos \theta +{\widehat {u}}{\widehat {\ \!v}}\sin \theta )$

By designating the unit bivector of this plane as the imaginary number

${i}={\widehat {u}}{\widehat {\ \!v}}={\widehat {u}}\wedge {\widehat {\ \!v}}$

$i^{2}=-1$

this path vector can be conveniently written in complex exponential form

$\mathbf {r} =r{\widehat {u}}e^{i\theta }$

and the derivative with respect to angle is

${\frac {d\mathbf {r} }{d\theta }}=r{\widehat {u}}ie^{i\theta }=\mathbf {r} i.$

The cross product in relation to the exterior product. In red are the unit normal vector, and the "parallel" unit bivector.

For example, torque is generally defined as the magnitude of the perpendicular force component times distance, or work per unit angle. Thus the torque, the rate of change of work⁠$W$⁠with respect to angle, due to a force⁠$F$⁠,is

$\tau ={\frac {dW}{d\theta }}=F\cdot {\frac {dr}{d\theta }}=F\cdot (\mathbf {r} i).$

Rotational quantities are represented invector calculusin three dimensions using thecross product.Together with a choice of an oriented volume form⁠$I$⁠,these can be related to the exterior product with its more natural geometric interpretation of such quantities as a bivectors by using thedualrelationship

$a\times b=-I(a\wedge b).$

Unlike the cross product description of torque,⁠$\tau =\mathbf {r} \times F$⁠,the geometric algebra description does not introduce a vector in the normal direction; a vector that does not exist in two and that is not unique in greater than three dimensions. The unit bivector describes the plane and the orientation of the rotation, and the sense of the rotation is relative to the angle between the vectors⁠${\widehat {u}}$⁠and⁠${\widehat {\ \!v}}$⁠.

Geometric calculus

Main article:Geometric calculus

Geometric calculus extends the formalism to include differentiation and integration including differential geometry anddifferential forms.

Essentially, the vector derivative is defined so that the GA version ofGreen's theoremis true,

$\int _{A}dA\,\nabla f=\oint _{\partial A}dx\,f$

and then one can write

$\nabla f=\nabla \cdot f+\nabla \wedge f$

as a geometric product, effectively generalizingStokes' theorem(including the differential form version of it).

In 1D when⁠$A$⁠is a curve with endpoints⁠$a$⁠and⁠$b$⁠,then

$\int _{A}dA\,\nabla f=\oint _{\partial A}dx\,f$

reduces to

$\int _{a}^{b}dx\,\nabla f=\int _{a}^{b}dx\cdot \nabla f=\int _{a}^{b}df=f(b)-f(a)$

or the fundamental theorem of integral calculus.

Also developed are the concept ofvector manifoldand geometric integration theory (which generalizes differential forms).

History

Before the 20th century

Although the connection of geometry with algebra dates as far back at least toEuclid'sElementsin the third century B.C. (seeGreek geometric algebra), GA in the sense used in this article was not developed until 1844, when it was used in asystematic wayto describe the geometrical properties andtransformationsof a space. In that year,Hermann Grassmannintroduced the idea of a geometrical algebra in full generality as a certain calculus (analogous to thepropositional calculus) that encoded all of the geometrical information of a space.Grassmann's algebraic system could be applied to a number of different kinds of spaces, the chief among them beingEuclidean space,affine space,andprojective space.Following Grassmann, in 1878William Kingdon Cliffordexamined Grassmann's algebraic system alongside thequaternionsofWilliam Rowan Hamiltonin (Clifford 1878). From his point of view, the quaternions described certaintransformations(which he calledrotors), whereas Grassmann's algebra described certainproperties(orStreckensuch as length, area, and volume). His contribution was to define a new product – thegeometric product– on an existing Grassmann algebra, which realized the quaternions as living within that algebra. Subsequently,Rudolf Lipschitzin 1886 generalized Clifford's interpretation of the quaternions and applied them to the geometry of rotations in⁠$n$⁠dimensions. Later these developments would lead other 20th-century mathematicians to formalize and explore the properties of the Clifford algebra.

Nevertheless, another revolutionary development of the 19th-century would completely overshadow the geometric algebras: that ofvector analysis,developed independently byJosiah Willard GibbsandOliver Heaviside.Vector analysis was motivated byJames Clerk Maxwell's studies ofelectromagnetism,and specifically the need to express and manipulate conveniently certaindifferential equations.Vector analysis had a certain intuitive appeal compared to the rigors of the new algebras. Physicists and mathematicians alike readily adopted it as their geometrical toolkit of choice, particularly following the influential 1901 textbookVector AnalysisbyEdwin Bidwell Wilson,following lectures of Gibbs.

In more detail, there have been three approaches to geometric algebra:quaternionicanalysis, initiated by Hamilton in 1843 and geometrized as rotors by Clifford in 1878; geometric algebra, initiated by Grassmann in 1844; and vector analysis, developed out of quaternionic analysis in the late 19th century by Gibbs and Heaviside. The legacy of quaternionic analysis in vector analysis can be seen in the use of⁠$i$⁠,⁠$j$⁠,⁠$k$⁠to indicate the basis vectors of⁠$\mathbf {R} ^{3}$⁠:it is being thought of as the purely imaginary quaternions. From the perspective of geometric algebra, the even subalgebra of the Space Time Algebra is isomorphic to the GA of 3D Euclidean space and quaternions are isomorphic to the even subalgebra of the GA of 3D Euclidean space, which unifies the three approaches.

20th century and present

Progress on the study of Clifford algebras quietly advanced through the twentieth century, although largely due to the work ofabstract algebraistssuch asÉlie Cartan,Hermann WeylandClaude Chevalley.Thegeometricalapproach to geometric algebras has seen a number of 20th-century revivals. In mathematics,Emil Artin'sGeometric Algebradiscusses the algebra associated with each of a number of geometries, includingaffine geometry,projective geometry,symplectic geometry,andorthogonal geometry.In physics, geometric algebras have been revived as a "new" way to do classical mechanics and electromagnetism, together with more advanced topics such as quantum mechanics and gauge theory.David Hestenesreinterpreted thePauliandDiracmatrices as vectors in ordinary space and spacetime, respectively, and has been a primary contemporary advocate for the use of geometric algebra.

Incomputer graphicsand robotics, geometric algebras have been revived in order to efficiently represent rotations and other transformations. For applications of GA in robotics (screw theory,kinematics and dynamics using versors), computer vision, control and neural computing (geometric learning) see Bayro (2010).

See also

• Comparison of vector algebra and geometric algebra
• Clifford algebra
• Grassmann–Cayley algebra
• Spacetime algebra
• Spinor
• Quaternion
• Algebra of physical space
• Universal geometric algebra

References and further reading

Arranged chronologically

• Grassmann, Hermann(1844),Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert,Leipzig: O. Wigand,OCLC20521674
• Clifford, Professor (1878), "Applications of Grassmann's Extensive Algebra",American Journal of Mathematics,1(4): 350–358,doi:10.2307/2369379,JSTOR2369379
• Artin, Emil(1988) [1957],Geometric algebra,Wiley Classics Library, Wiley,doi:10.1002/9781118164518,ISBN978-0-471-60839-4,MR1009557
• Hestenes, David(1966),Space–time Algebra,Gordon and Breach,ISBN978-0-677-01390-9,OCLC996371
• Wheeler, J. A.; Misner, C.; Thorne, K. S. (1973),Gravitation,W.H. Freeman,ISBN978-0-7167-0344-0
• Bourbaki, Nicolas(1980), "Ch. 9" Algèbres de Clifford "",Eléments de Mathématique. Algèbre,Hermann,ISBN9782225655166
• Hestenes, David;Sobczyk, Garret (1984),Clifford Algebra to Geometric Calculus, a Unified Language for Mathematics and Physics,Springer Netherlands,ISBN978-90-277-1673-6
• Hestenes, David(1986), "A Unified Language for Mathematics and Physics", in J.S.R. Chisholm; A.K. Commons (eds.),Clifford Algebras and Their Applications in Mathematical Physics,NATO ASI Series (Series C), vol. 183, Springer, pp. 1–23,doi:10.1007/978-94-009-4728-3_1,ISBN978-94-009-4728-3
• Wilmot, G.P. (1988a),The Structure of Clifford algebra. Journal of Mathematical Physics,vol. 29, pp. 2338–2345
• Wilmot, G.P. (1988b), "Clifford algebra and the Pfaffian expansion",Journal of Mathematical Physics,29:2346–2350,doi:10.1063/1.528118
• Chevalley, Claude (1991),The Algebraic Theory of Spinors and Clifford Algebras, Collected Works,vol. 2, Springer,ISBN3-540-57063-2
• Doran, Chris J. L.(1994),Geometric Algebra and its Application to Mathematical Physics(PhD thesis),University of Cambridge,doi:10.17863/CAM.16148,hdl:1810/251691,OCLC53604228
• Baylis, W. E., ed. (2011) [1996],Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering,Birkhäuser,ISBN9781461241058
• Aragón, G.; Aragón, J.L.; Rodríguez, M.A. (1997), "Clifford Algebras and Geometric Algebra",Advances in Applied Clifford Algebras,7(2): 91–102,doi:10.1007/BF03041220,S2CID120860757
• Hestenes, David(1999),New Foundations for Classical Mechanics(2nd ed.), Springer Verlag,ISBN978-0-7923-5302-7
• Lasenby, Joan; Lasenby, Anthony N.;Doran, Chris J. L.(2000),"A Unified Mathematical Language for Physics and Engineering in the 21st Century"(PDF),Philosophical Transactions of the Royal Society A,358(1765): 21–39,Bibcode:2000RSPTA.358...21L,doi:10.1098/rsta.2000.0517,S2CID91884543,archived(PDF)from the original on 2015-03-19
• Lounesto, Pertti (2001),Clifford Algebras and Spinors(2nd ed.),Cambridge University Press,ISBN978-0-521-00551-7
• Baylis, W. E. (2002),Electrodynamics: A Modern Geometric Approach(2nd ed.),Birkhäuser,ISBN978-0-8176-4025-5
• Dorst, Leo (2002), "The Inner Products of Geometric Algebra", in Dorst, L.; Doran, C.; Lasenby, J. (eds.),Applications of Geometric Algebra in Computer Science and Engineering,Birkhäuser,pp. 35–46,doi:10.1007/978-1-4612-0089-5_2,ISBN978-1-4612-0089-5
• Doran, Chris J. L.;Lasenby, Anthony N. (2003),Geometric Algebra for Physicists(PDF),Cambridge University Press,ISBN978-0-521-71595-9,archived(PDF)from the original on 2009-01-06
• Hestenes, David(2003),"Oersted Medal Lecture 2002: Reforming the Mathematical Language of Physics"(PDF),Am. J. Phys.,71(2): 104–121,Bibcode:2003AmJPh..71..104H,CiteSeerX10.1.1.649.7506,doi:10.1119/1.1522700{{citation}}:CS1 maint: url-status (link)
• Hildenbrand, Dietmar; Fontijne, Daniel; Perwass, Christian; Dorst, Leo (2004),"Geometric Algebra and its Application to Computer Graphics"(PDF),Proceedings of Eurographics 2004,doi:10.2312/egt.20041032,archived(PDF)from the original on 2015-09-06
• Lasenby, Anthony (2004), "Conformal Models of de Sitter Space, Initial Conditions for Inflation and the CMB",AIP Conference Proceedings,vol. 736, pp. 53–70,arXiv:astro-ph/0411579,doi:10.1063/1.1835174,S2CID18034896
• Hestenes, David (2005),Introduction to Primer for Geometric Algebra
• Selig, J.M. (2005).Geometric Fundamentals of Robotics.Monographs in Computer Science. New York, NY: Springer New York.doi:10.1007/b138859.ISBN978-0-387-20874-9.
• Bain, J. (2006), "Spacetime structuralism: §5 Manifoldsvs.geometric algebra ", inDennis Dieks(ed.),The ontology of spacetime,Elsevier, p. 54ff,ISBN978-0-444-52768-4
• Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2007),Geometric algebra for computer science: an object-oriented approach to geometry,Elsevier,ISBN978-0-12-369465-2,OCLC132691969
• Penrose, Roger(2007),The Road to Reality,Vintage books,ISBN978-0-679-77631-4
• Francis, Matthew R.; Kosowsky, Arthur (2008), "The Construction of Spinors in Geometric Algebra",Annals of Physics,317(2): 383–409,arXiv:math-ph/0403040v2,Bibcode:2005AnPhy.317..383F,doi:10.1016/j.aop.2004.11.008,S2CID119632876
• Li, Hongbo (2008),Invariant Algebras and Geometric Reasoning,World Scientific,ISBN9789812770110.Chapter 1as PDF
• Vince, John A. (2008),Geometric Algebra for Computer Graphics,Springer,ISBN978-1-84628-996-5
• Lundholm, Douglas; Svensson, Lars (2009), "Clifford Algebra, Geometric Algebra and Applications",arXiv:0907.5356v1[math-ph]
• Perwass, Christian (2009),Geometric Algebra with Applications in Engineering,Geometry and Computing, vol. 4,Bibcode:2009gaae.book.....P,doi:10.1007/978-3-540-89068-3,ISBN978-3-540-89067-6
• Selig, J. M. (2000),"Clifford algebra of points, lines and planes"(PDF),Robotica,18(5): 545–556,doi:10.1017/S0263574799002568,S2CID28929170
• Bayro-Corrochano, Eduardo (2010),Geometric Computing for Wavelet Transforms, Robot Vision, Learning, Control and Action,Springer Verlag,ISBN9781848829299
• Bayro-Corrochano, E.; Scheuermann, Gerik, eds. (2010),Geometric Algebra Computing in Engineering and Computer Science,Springer,ISBN9781849961080Extract online athttps://davidhestenes.net/geocalc/html/UAFCG.html#5 New Tools for Computational Geometry and rejuvenation of Screw Theory
• Goldman, Ron (2010),Rethinking Quaternions: Theory and Computation,Morgan & Claypool, Part III. Rethinking Quaternions and Clifford Algebras,ISBN978-1-60845-420-4
• Dorst, Leo.; Lasenby, Joan (2011),Guide to Geometric Algebra in Practice,Springer,ISBN9780857298119
• Macdonald, Alan (2011),Linear and Geometric Algebra,CreateSpace,ISBN9781453854938,OCLC704377582
• Snygg, John (2011),A New Approach to Differential Geometry using Clifford's Geometric Algebra,Springer,ISBN978-0-8176-8282-8
• Hildenbrand, Dietmar (2012), "Foundations of Geometric Algebra computing",Numerical Analysis and Applied Mathematics Icnaam 2012: International Conference of Numerical Analysis and Applied Mathematics,AIP Conference Proceedings,1479(1): 27–30,Bibcode:2012AIPC.1479...27H,doi:10.1063/1.4756054
• Sokolov, Andrey (2013),Clifford algebra and the projective model of Minkowski (Pseudo-Euclidean) spaces,arXiv:1307.4179
• Bromborsky, Alan (2014),An introduction to Geometric Algebra and Calculus(PDF),archived(PDF)from the original on 2019-10-15
• Klawitter, Daniel (2015),Clifford Algebras,doi:10.1007/978-3-658-07618-4,ISBN978-3-658-07617-7
• Kanatani, Kenichi (2015),Understanding Geometric Algebra: Hamilton, Grassmann, and Clifford for Computer Vision and Graphics,CRC Press,ISBN978-1-4822-5951-3
• Li, Hongbo; Huang, Lei; Shao, Changpeng; Dong, Lei (2015), "Three-Dimensional Projective Geometry with Geometric Algebra",arXiv:1507.06634v1[math.MG]
• Hestenes, David (2017), "The Genesis of Geometric Algebra: A Personal Retrospective",Advances in Applied Clifford Algebras,27:351–379,doi:10.1007/s00006-016-0664-z,S2CID253592888
• Dorst, Leo (2016), "3D Oriented Projective Geometry Through Versors of⁠$\mathbb {R} ^{3,3}$⁠",Advances in Applied Clifford Algebras,26(4): 1137–1172,doi:10.1007/s00006-015-0625-y
• Vaz, Jayme; da Rocha, Roldão (2016),An Introduction to Clifford Algebras and Spinors,Oxford University Press,Bibcode:2016icas.book.....V,ISBN978-0-19-878292-6
• Easter, Robert Benjamin; Hitzer, Eckhard (2017), "Double Conformal Geometric Algebra",Advances in Applied Clifford Algebras,27(3): 2175–2199,doi:10.1007/s00006-017-0784-0,S2CID253600526
• Du, Juan; Goldman, Ron; Mann, Stephen (2017), "Modeling 3D Geometry in the Clifford Algebra R(4, 4)",Advances in Applied Clifford Algebras,27(4): 3039–3062,doi:10.1007/s00006-017-0798-7,S2CID253587390
• Bayro-Corrochano, Eduardo (2018).Computer Vision, Graphics and Neurocomputing.Geometric Algebra Applications. Vol. I. Springer.ISBN978-3-319-74830-6.
• Breuils, Stéphane (2018).Structure algorithmique pour les opérateurs d'Algèbres Géométriques et application aux surfaces quadriques(PDF)(PHD). université-paris-est.Archived(PDF)from the original on 2019-07-14.
• Lavor, Carlile; Xambó-Descamps, Sebastià; Zaplana, Isiah (2018).A Geometric Algebra Invitation to Space-Time Physics, Robotics and Molecular Geometry.Springer. pp. 1–.ISBN978-3-319-90665-2.
• Hrdina, Jaroslav; Návrat, Aleš; Vašík, Petr (2018), "Geometric Algebra for Conics",Advances in Applied Clifford Algebras,28(3),doi:10.1007/s00006-018-0879-2,S2CID125649450
• Breuils, Stéphane; Fuchs, Laurent; Hitzer, Eckhard; Nozick, Vincent; Sugimoto, Akihiro (2019),"Three-dimensional quadrics in extended conformal geometric algebras of higher dimensions from control points, implicit equations and axis alignment"(PDF),Advances in Applied Clifford Algebras,29(3),doi:10.1007/s00006-019-0974-z,S2CID253597480
• Josipović, Miroslav (2019).Geometric Multiplication of Vectors: An Introduction to Geometric Algebra in Physics.Springer International Publishing;Birkhäuser. p. 256.ISBN978-3-030-01756-9.
• Hadfield, Hugo; Lasenby, Joan (2020),"Constrained Dynamics in Conformal and Projective Geometric Algebra",Advances in Computer Graphics,Lecture Notes in Computer Science, vol. 12221, pp. 459–471,doi:10.1007/978-3-030-61864-3_39,ISBN978-3-030-61863-6,S2CID224820480
• Wu, Bofeng (2022), "A signature invariant geometric algebra framework for spacetime physics and its applications in relativistic dynamics of a massive particle and gyroscopic precession",Scientific Reports,12(1): 3981,arXiv:2111.07353,Bibcode:2022NatSR..12.3981W,doi:10.1038/s41598-022-06895-0,PMC8901677,PMID35256628
• Wilmot, G.P. (2023)."The Algebra Of Geometry".GitHub.
• Lengyel, Eric (2024).Projective Geometric Algebra Illuminated.Lincoln, California: Terathon Software LLC.ISBN979-8-9853582-5-4.

External links

• A Survey of Geometric Algebra and Geometric CalculusAlan Macdonald,Luther College, Iowa.
• Imaginary Numbers are not Real – the Geometric Algebra of Spacetime.Introduction (Cambridge GA group).
• Geometric Algebra 2015, Masters Course in Scientific Computing,from Dr. Chris Doran (Cambridge).
• Maths for (Games) Programmers: 5 – Multivector methods.Comprehensive introduction and reference for programmers, fromIan Bell.
• IMPA Summer School 2010Fernandes Oliveira Intro and Slides.
• University of FukuiE.S.M. Hitzer and Japan GA publications.
• Google Group for GA
• Geometric Algebra PrimerIntroduction to GA, Jaap Suter.
• Geometric Algebra Resourcescurated wiki, Pablo Bleyer.
• Applied Geometric Algebras in Computer Science and Engineering 2018Early Proceedings
• bivector.netGeometric Algebra for CGI, Vision and Engineering community website
• AGACSE 2021 Videos

English translations of early books and papers

• G. Combebiac, "calculus of tri-quaternions"(Doctoral dissertation)
• M. Markic, "Transformants: A new mathematical vehicle. A synthesis of Combebiac's tri-quaternions and Grassmann's geometric system. The calculus of quadri-quaternions"
• C. Burali-Forti, "The Grassmann method in projective geometry"A compilation of three notes on the application of exterior algebra to projective geometry
• C. Burali-Forti, "Introduction to Differential Geometry, following the method of H. Grassmann"Early book on the application of Grassmann algebra
• H. Grassmann, "Mechanics, according to the principles of the theory of extension"One of his papers on the applications of exterior algebra.

Research groups

• Geometric Calculus International.Links to Research groups, Software, and Conferences, worldwide.
• Cambridge Geometric Algebra group.Full-text online publications, and other material.
• University of Amsterdam group
• Geometric Calculus research & development(archive of Hestenes's website at Arizona State University).
• GA-Net blogandnewsletter archive.Geometric Algebra/Clifford Algebra development news.
• Geometric Algebra for Perception Action Systems. Geometric Cybernetics Group(CINVESTAV, Campus Guadalajara, Mexico).