Hearing the shape of a drum

Mathematically ideal drums with membranes of these two different shapes (but otherwise identical) would sound the same, because theeigenfrequenciesare all equal, so thetimbral spectrawould contain the same overtones. This example was constructed by Gordon, Webb and Wolpert. Notice that both polygons have the same area and perimeter.

Tohear the shape of a drumis to infer information about the shape of thedrumheadfrom the sound it makes, i.e., from the list ofovertones,via the use ofmathematicaltheory.

"Can One Hear the Shape of a Drum?" is the title of a 1966 article byMark Kacin theAmerican Mathematical Monthlywhich made the question famous, though this particular phrasing originates withLipman Bers.Similar questions can be traced back all the way to physicistArthur Schusterin 1882.For his paper, Kac was given theLester R. Ford Awardin 1967 and theChauvenet Prizein 1968.

The frequencies at which a drumhead can vibrate depend on its shape. TheHelmholtz equationcalculates the frequencies if the shape is known. These frequencies are theeigenvaluesof theLaplacianin the space. A central question is whether the shape can be predicted if the frequencies are known; for example, whether aReuleaux trianglecan be recognized in this way.Kac admitted that he did not know whether it was possible for two different shapes to yield the same set of frequencies. The question of whether the frequencies determine the shape was finally answered in the negative in the early 1990s by Gordon, Webb and Wolpert.

Formal statement

More formally, the drum is conceived as an elastic membrane whose boundary is clamped. It is represented as adomainDin theplane.Denote byλ_ntheDirichlet eigenvaluesforD:that is, theeigenvaluesof theDirichlet problemfor theLaplacian:

${\begin{cases}\Delta u+\lambda u=0\\u|_{\partial D}=0\end{cases}}$

Two domains are said to beisospectral(or homophonic) if they have the same eigenvalues. The term "homophonic" is justified because the Dirichlet eigenvalues are precisely the fundamental tones that the drum is capable of producing: they appear naturally asFourier coefficientsin the solutionwave equationwith clamped boundary.

Therefore, the question may be reformulated as: what can be inferred onDif one knows only the values ofλ_n?Or, more specifically: are there two distinct domains that are isospectral?

Related problems can be formulated for the Dirichlet problem for the Laplacian on domains in higher dimensions or onRiemannian manifolds,as well as for otherelliptic differential operatorssuch as theCauchy–Riemann operatororDirac operator.Other boundary conditions besides the Dirichlet condition, such as theNeumann boundary condition,can be imposed. Seespectral geometryandisospectralas related articles.

The answer

One-parameter family of isospectral drums

Eigenmodes and corresponding eigenvalues of the Laplace operator on the GWW domains

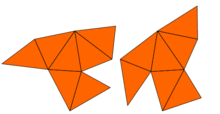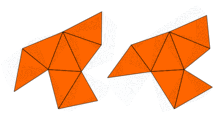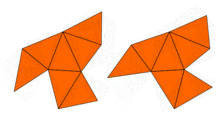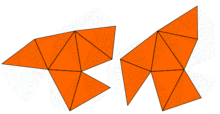
In 1964,John Milnorobserved that a theorem on lattices due toErnst Wittimplied the existence of a pair of 16-dimensional flat tori that have the same eigenvalues but different shapes. However, the problem in two dimensions remained open until 1992, whenCarolyn Gordon,David Webb,and Scott Wolpert constructed, based on theSunada method,a pair of regions in the plane that have different shapes but identical eigenvalues. The regions areconcave polygons.The proof that both regions have the same eigenvalues uses the symmetries of the Laplacian. This idea has been generalized by Buser, Conway, Doyle, and Semmlerwho constructed numerous similar examples. So, the answer to Kac's question is: for many shapes, one cannot hear the shape of the drumcompletely.However, some information can be inferred.

On the other hand,Steve Zelditchproved that the answer to Kac's question is positive if one imposes restrictions to certainconvexplanar regions withanalyticboundary. It is not known whether two non-convex analytic domains can have the same eigenvalues. It is known that the set of domains isospectral with a given one is compact in the C^∞topology. Moreover, the sphere (for instance) is spectrally rigid, byCheng's eigenvalue comparison theorem.It is also known, by a result of Osgood, Phillips, and Sarnak that the moduli space ofRiemann surfacesof a given genus does not admit a continuous isospectral flow through any point, and is compact in the Fréchet–Schwartz topology.

Weyl's formula

Main article:Weyl law

Weyl's formula states that one can infer the areaAof the drum by counting how rapidly theλ_ngrow. We defineN(R) to be the number of eigenvalues smaller thanRand we get

$A=\omega _{d}^{-1}(2\pi )^{d}\lim _{R\to \infty }{\frac {N(R)}{R^{d/2}}},$

wheredis the dimension, and$\omega _{d}$is the volume of thed-dimensional unit ball. Weyl also conjectured that the next term in the approximation below would give the perimeter ofD.In other words, ifLdenotes the length of the perimeter (or the surface area in higher dimension), then one should have

$N(R)=(2\pi )^{-d}\omega _{d}AR^{d/2}\mp {\frac {1}{4}}(2\pi )^{-d+1}\omega _{d-1}LR^{(d-1)/2}+o(R^{(d-1)/2}).$

For a smooth boundary, this was proved byVictor Ivriiin 1980. The manifold is also not allowed to have a two-parameter family of periodic geodesics, such as a sphere would have.

The Weyl–Berry conjecture

For non-smooth boundaries,Michael Berryconjectured in 1979 that the correction should be of the order of

$R^{D/2},$

whereDis theHausdorff dimensionof the boundary. This was disproved by J. Brossard and R. A. Carmona, who then suggested that one should replace the Hausdorff dimension with theupper box dimension.In the plane, this was proved if the boundary has dimension 1 (1993), but mostly disproved for higher dimensions (1996); both results are byLapidusandPomerance.

See also

• Gassmann triple
• Isospectral
• Spectral geometry
• Vibrations of a circular membrane

References

• Abikoff, William (January 1995),"Remembering Lipman Bers"(PDF),Notices of the AMS,42(1): 8–18
• Brossard, Jean; Carmona, René (1986),"Can one hear the dimension of a fractal?",Comm. Math. Phys.,104(1): 103–122,Bibcode:1986CMaPh.104..103B,doi:10.1007/BF01210795,S2CID121173871
• Buser, Peter;Conway, John;Doyle, Peter; Semmler, Klaus-Dieter (1994), "Some planar isospectral domains",International Mathematics Research Notices,1994(9): 391–400,doi:10.1155/S1073792894000437
• Chapman, S.J. (1995), "Drums that sound the same",American Mathematical Monthly,102(February): 124–138,doi:10.2307/2975346,JSTOR2975346
• Giraud, Olivier;Thas, Koen(2010), "Hearing shapes of drums – mathematical and physical aspects of isospectrality",Reviews of Modern Physics,82(3): 2213–2255,arXiv:1101.1239,Bibcode:2010RvMP...82.2213G,doi:10.1103/RevModPhys.82.2213,S2CID119289493
• Gordon, Carolyn;Webb, David(1996), "You can't hear the shape of a drum",American Scientist,84(January–February): 46–55,Bibcode:1996AmSci..84...46G
• Gordon, C.;Webb, D.;Wolpert, S. (1992), "Isospectral plane domains and surfaces via Riemannian orbifolds",Inventiones Mathematicae,110(1): 1–22,Bibcode:1992InMat.110....1G,doi:10.1007/BF01231320,S2CID122258115
• Ivrii, V. Ja. (1980), "The second term of the spectral asymptotics for a Laplace–Beltrami operator on manifolds with boundary",Funktsional. Anal. I Prilozhen,14(2): 25–34,doi:10.1007/BF01086550,S2CID123935462(InRussian).
• Kac, Mark(April 1966),"Can One Hear the Shape of a Drum?"(PDF),American Mathematical Monthly,73(4, part 2): 1–23,doi:10.2307/2313748,JSTOR2313748
• Lapidus, Michel L. (1991), "Can One Hear the Shape of a Fractal Drum? Partial Resolution of the Weyl-Berry Conjecture",Geometric Analysis and Computer Graphics,Math. Sci. Res. Inst. Publ., vol. 17, New York: Springer, pp. 119–126,doi:10.1007/978-1-4613-9711-3_13,ISBN978-1-4613-9713-7
• Lapidus, Michel L. (1993), "Vibrations of fractal drums, theRiemann hypothesis,waves in fractal media, and the Weyl–Berry conjecture ", in B. D. Sleeman; R. J. Jarvis (eds.),Ordinary and Partial Differential Equations, Vol IV, Proc. Twelfth Internat. Conf. (Dundee, Scotland, UK, June 1992),Pitman Research Notes in Math. Series, vol. 289, London: Longman and Technical, pp. 126–209
• Lapidus, M. L.; van Frankenhuysen, M. (2000),Fractal Geometry and Number Theory: Complex dimensions of fractal strings and zeros of zeta functions,Boston: Birkhauser.(Revised and enlarged second edition to appear in 2005.)
• Lapidus, Michel L.; Pomerance, Carl (1993),"The Riemann zeta-function and the one-dimensional Weyl-Berry conjecture for fractal drums",Proc. London Math. Soc.,Series 3,66(1): 41–69,CiteSeerX10.1.1.526.854,doi:10.1112/plms/s3-66.1.41
• Lapidus, Michel L.; Pomerance, Carl (1996), "Counterexamples to the modified Weyl–Berry conjecture on fractal drums",Math. Proc. Cambridge Philos. Soc.,119(1): 167–178,Bibcode:1996MPCPS.119..167L,doi:10.1017/S0305004100074053,S2CID33567484
• Milnor, John(1964), "Eigenvalues of the Laplace operator on certain manifolds",Proceedings of the National Academy of Sciences of the United States of America,51(4): 542ff,Bibcode:1964PNAS...51..542M,doi:10.1073/pnas.51.4.542,PMC300113,PMID16591156
• Sunada, T.(1985), "Riemannian coverings and isospectral manifolds",Ann. of Math.,2,121(1): 169–186,doi:10.2307/1971195,JSTOR1971195
• Zelditch, S. (2000), "Spectral determination of analytic bi-axisymmetric plane domains",Geometric and Functional Analysis,10(3): 628–677,arXiv:math/9901005,doi:10.1007/PL00001633,S2CID16324240

External links

• Simulationshowing solutions of the wave equation in two isospectral drums
• Isospectral Drumsby Toby Driscoll at the University of Delaware
• Some planar isospectral domainsby Peter Buser,John Horton Conway,Peter Doyle, and Klaus-Dieter Semmler
  • 3D rendering of the Buser-Conway-Doyle-Semmler homophonic drums
• Drums That Sound Alikeby Ivars Peterson at the Mathematical Association of America web site
• Weisstein, Eric W.,"Isospectral Manifolds",MathWorld
• Benguria, Rafael D. (2001) [1994],"Dirichlet eigenvalue",Encyclopedia of Mathematics,EMS Press